Дерево потомков (теория групп) - Википедия - Descendant tree (group theory)

В математике, в частности теория групп, а потомок это иерархическая структура для визуализации отношений родитель-потомок между классы изоморфизма конечных групп простого степенного порядка ${ displaystyle p ^ {n}}$, для фиксированного простого числа ${ displaystyle p}$ и различные целые показатели ${ Displaystyle п geq 0}$.Такие группы кратко называются конечный p-группы. вершины из потомок являются классами изоморфизма конечных п-группы.

В дополнение к их порядок ${ displaystyle p ^ {n}}$, конечный п-группы имеют еще два связанных инварианта: класс нильпотентности ${ displaystyle c}$ и кокласс ${ Displaystyle г = п-с}$Оказалось, что деревья-потомки определенного вида, так называемые обрезанные коклассовые деревья бесконечно много вершин которого имеют общий кокласс ${ displaystyle r}$, обнаруживают повторяющийся конечный образец. Эти два важнейших свойства конечность и периодичностьдопускают характеризацию всех членов дерева конечным числом параметризованных презентации Следовательно, деревья-потомки играют фундаментальную роль в классификации конечных п-группы. С помощью ядер и таргетов Гомоморфизмы переноса Артина, деревья-потомки могут быть наделены дополнительной структурой.

Важный вопрос - как дерево потомков ${ Displaystyle { mathcal {T}} (R)}$ фактически может быть построена для назначенной стартовой группы, которая берется за корень ${ displaystyle R}$ дерева. палгоритм генерации группы рекурсивный процесс построения дерева потомков данного конечного п-группа, играющая роль корня дерева. Этот алгоритм реализован в системах вычислительной алгебры. ЗАЗОР и Магма.

Определения и терминология

По словам М. Ф. Ньюмана,^[1]существует несколько различных определений родитель ${ Displaystyle pi (G)}$конечного п-группа ${ displaystyle G}$.Общий принцип - формирование частное ${ Displaystyle pi (G) = G / N}$ из ${ displaystyle G}$подходящим нормальная подгруппа ${ Displaystyle N треугольникleft G}$который может быть либо

п

1. то центр ${ Displaystyle N = zeta _ {1} (G)}$ из ${ displaystyle G}$откуда ${ Displaystyle pi (G) = G / zeta _ {1} (G)}$ называется центральное частное из ${ displaystyle G}$, или же
2. последний нетривиальный член ${ Displaystyle N = гамма _ {с} (G)}$ из нижний центральный ряд из ${ displaystyle G}$, куда ${ displaystyle c}$ обозначает класс нильпотентности ${ displaystyle G}$, или же
3. последний нетривиальный член ${ Displaystyle N = P_ {c-1} (G)}$ из нижний показательп центральная серия из ${ displaystyle G}$, куда ${ displaystyle c}$ обозначает показатель -п класс ${ displaystyle G}$, или же
4. последний нетривиальный член ${ Displaystyle N = G ^ {(d-1)}}$ из производный ряд из ${ displaystyle G}$, куда ${ displaystyle d}$ обозначает производную длину ${ displaystyle G}$.

В каждом случае,${ displaystyle G}$ называется непосредственный потомок из ${ Displaystyle pi (G)}$и направленный край дерева определяется либо ${ Displaystyle G к pi (G)}$в направлении каноническая проекция ${ displaystyle pi: G to pi (G)}$ на частное ${ Displaystyle pi (G) = G / N}$или по ${ Displaystyle пи (G) к G}$ в противоположном направлении, что более характерно для деревьев-потомков. Первая конвенция принята К. Р. Лидхэм-Грином и М. Ф. Ньюманом,^[2]М. дю Сотуа и Д. Сигал,^[3]К. Р. Лидхэм-Грин и С. Маккей,^[4]и Б. Эйком, К. Р. Лидхэм-Грином, М. Ф. Ньюманом и Э. А. О'Брайеном.^[5]Последнее определение используется М. Ф. Ньюманом,^[1]М. Ф. Ньюман и Э. А. О'Брайен,^[6]М. дю Сотуа,^[7]и Б. Эйком и К. Р. Лидхэм-Грином.^[8]

В дальнейшем направление канонических проекций выбирается для всех ребер. Затем, в более общем смысле, вершина ${ displaystyle R}$ это потомок вершины ${ displaystyle P}$,и ${ displaystyle P}$ является предок из ${ displaystyle R}$, если либо ${ displaystyle R}$ равно ${ displaystyle P}$или есть дорожка

${ displaystyle (1) qquad R = Q_ {0} to Q_ {1} to cdots to Q_ {m-1} to Q_ {m} = P}$, с ${ Displaystyle м geq 1}$,

направленных кромок от ${ displaystyle R}$ к ${ displaystyle P}$Вершины, образующие путь, обязательно совпадают с повторные родители ${ Displaystyle Q_ {j} = pi ^ {j} (R)}$ из ${ displaystyle R}$, с ${ Displaystyle 0 Leq J Leq M}$:

${ Displaystyle (2) qquad R = pi ^ {0} (R) to pi ^ {1} (R) to cdots to pi ^ {m-1} (R) to pi ^ {m} (R) = P}$, с ${ Displaystyle м geq 1}$,

В наиболее важном частном случае (P2) родителей, определенных как последние нетривиальные нижние центральные частные, их также можно рассматривать как последовательные частные ${ Displaystyle R / гамма _ {с + 1-j} (R)}$ класса ${ displaystyle c-j}$ из ${ displaystyle R}$когда класс нильпотентности ${ displaystyle R}$ дан кем-то ${ displaystyle c geq m}$:

${ Displaystyle (3) qquad R simeq R / gamma _ {c + 1} (R) to R / gamma _ {c} (R) to cdots to R / gamma _ {c + 2-m} (R) to R / gamma _ {c + 1-m} (R) simeq P}$, с ${ Displaystyle с geq м geq 1}$.

Как правило, потомок ${ Displaystyle { mathcal {T}} (G)}$ вершины ${ displaystyle G}$ является поддеревом всех потомков ${ displaystyle G}$, начиная с корень ${ displaystyle G}$.Максимально возможное дерево потомков ${ Displaystyle { mathcal {T}} (1)}$ тривиальной группы ${ displaystyle 1}$ содержит все конечные п-группы и несколько исключительны, поскольку для любого родительского определения (P1 – P4) тривиальная группа ${ displaystyle 1}$ имеет бесконечно много абелевых п-группы как его непосредственные потомки. Родительские определения (P2 – P3) имеют то преимущество, что любые нетривиальные конечные п-группа (порядка кратного ${ displaystyle p}$) имеет только конечное число непосредственных потомков.

Pro-п группы и коклассовые деревья

Для четкого понимания коклассовые деревья как частный пример деревьев-потомков, необходимо обобщить некоторые факты, касающиеся бесконечного топологический про-п группы.Участники ${ displaystyle gamma _ {j} (S)}$, с ${ displaystyle j geq 1}$, нижнего центрального ряда про-п группа ${ displaystyle S}$- замкнутые (и открытые) подгруппы конечного индекса, поэтому соответствующие фактор-группы ${ Displaystyle S / gamma _ {j} (S)}$ конечны п-группы.п группа ${ displaystyle S}$ говорят, что из кокласс ${ Displaystyle mathrm {cc} (S) = r}$когда предел ${ displaystyle r = lim _ {j to infty} , mathrm {cc} (S / gamma _ {j} (S))}$ кокласса последовательных частных существует и конечна.п группа ${ displaystyle S}$ кокласса ${ displaystyle r}$ это п-адический пре-космическая группа,^[5]так как он имеет нормальную подгруппу ${ displaystyle T}$, то группа переводов, который является свободным модулем над кольцом ${ displaystyle mathbb {Z} _ {p}}$ из п-адические целые числа однозначно определенный классифицировать ${ displaystyle d}$, то измерение, такое, что частное ${ Displaystyle P = S / T}$ конечный п-группа, точечная группа, который действует на ${ displaystyle T}$ однорядно.Размер определяется выражением

${ Displaystyle (4) qquad d = (p-1) p ^ {s}}$, с некоторыми ${ displaystyle 0 leq s$.

Центральный конечность результат для бесконечного про-п группы кокласса ${ displaystyle r}$ обеспечивается так называемым Теорема D, который является одним из пяти Теоремы кокласса доказано в 1994 г. независимо А. Шалевым^[9]и К. Р. Лидхэм-Грин,^[10]и предположили еще в 1980 г. К. Р. Лидхэм-Грин и М. Ф. Ньюман.^[2]Теорема D утверждает, что существует лишь конечное число классов изоморфизма бесконечных про-п группы кокласса ${ displaystyle r}$, для любого фиксированного простого числа ${ displaystyle p}$ и любое фиксированное неотрицательное целое число ${ displaystyle r}$Как следствие, если ${ displaystyle S}$ бесконечно про-п группа кокласса ${ displaystyle r}$, то существует минимальное целое число ${ displaystyle i geq 1}$ такое, что для любого целого числа выполняются следующие три условия ${ displaystyle j geq i}$.

S

1. ${ Displaystyle mathrm {cc} (S / gamma _ {j} (S)) = r}$,
2. ${ Displaystyle S / gamma _ {j} (S)}$ не является нижним центральным частным любого бесконечного про-п группа кокласса ${ displaystyle r}$ который не изоморфен ${ displaystyle S}$,
3. ${ Displaystyle gamma _ {j} / gamma _ {j + 1} (S)}$ цикличен по порядку ${ displaystyle p}$.

Потомковое дерево ${ Displaystyle { mathcal {T}} (R)}$относительно родительского определения (P2) корня ${ Displaystyle R = S / gamma _ {я} (S)}$ с минимальным ${ displaystyle i}$ называется коклассовое дерево ${ Displaystyle { mathcal {T}} (S)}$ из ${ displaystyle S}$и его единственный максимальный бесконечный (обратный) путь

${ Displaystyle (5) qquad R = S / gamma _ {я} (S) leftarrow S / gamma _ {я + 1} (S) leftarrow S / gamma _ {я + 2} (S ) leftarrow cdots}$

называется магистраль (или же хобот) дерева.

Рисунок 1: Потомковое дерево. Ветви B (2), B (4) имеют глубину 0, а B (5), B (7) соответственно. B (6), B (8) изоморфны как деревья.

Древовидная диаграмма

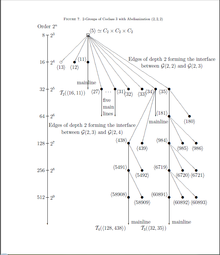
Дальнейшая терминология, используемая в диаграммах, визуализирующих конечные части деревьев-потомков, поясняется на рисунке 1 с помощью искусственного абстрактного дерева. уровень обозначает базовый нисходящий дизайн дерева-потомка. Для конкретных деревьев, таких как на рисунке 2, соответственно. На рисунке 3 и т. Д. Уровень обычно заменяется на шкала заказов возрастает сверху вниз. вершина способный (или же расширяемый), если у него есть хотя бы один непосредственный потомок, в противном случае он Терминал (или листВершины, имеющие общего родителя, называются братья и сестры.

Если дерево-потомок является коклассовым деревом ${ Displaystyle { mathcal {T}} (R)}$ с корнем ${ displaystyle R = R_ {0}}$и с вершинами mainline ${ Displaystyle (R_ {п}) _ {п geq 0}}$ помечены в соответствии с уровнем ${ displaystyle n}$, то конечное поддерево, определенное как разностное множество

${ displaystyle (6) qquad { mathcal {B}} (n) = { mathcal {T}} (R_ {n}) setminus { mathcal {T}} (R_ {n + 1})}$

называется пое отделение (или же веточка) дерева или также ответвляться ${ Displaystyle { mathcal {B}} (R_ {п})}$ с корнем ${ displaystyle R_ {n}}$, для любого ${ Displaystyle п geq 0}$. глубина ветви - это максимальная длина путей, соединяющих ее вершины с ее корнем. На рисунке 1 показано искусственное абстрактное коклассовое дерево, ветви которого ${ Displaystyle { mathcal {B}} (2)}$ и ${ Displaystyle { mathcal {B}} (4)}$ у обоих есть глубина ${ displaystyle 0}$, и ветви ${ Displaystyle { mathcal {B}} (5) simeq { mathcal {B}} (7)}$ и ${ Displaystyle { mathcal {B}} (6) simeq { mathcal {B}} (8)}$ попарно изоморфны как графы. Если все вершины глубины больше заданного целого числа ${ Displaystyle к geq 0}$ удалены из ветки ${ Displaystyle { mathcal {B}} (п)}$, то получаем глубину${ displaystyle k}$ обрезанная ветка ${ Displaystyle { mathcal {B}} _ {k} (п)}$. Соответственно, глубина${ displaystyle k}$ обрезанное коклассовое дерево ${ Displaystyle { mathcal {T}} _ {k} (R)}$, соотв. все коклассовое дерево ${ Displaystyle { mathcal {T}} (R)}$, состоит из бесконечной последовательности обрезанных ветвей ${ displaystyle ({ mathcal {B}} _ {k} (n)) _ {n geq 0}}$, соотв. ветви ${ Displaystyle ({ mathcal {B}} (п)) _ {п geq 0}}$, соединенных магистралью, вершины которой ${ displaystyle R_ {n}}$ называются бесконечно способный.

Виртуальная периодичность

Периодичность ветвей коклассовых деревьев с глубокой обрезкой доказана с помощью аналитические методы с использованием дзета-функций^[3]групп М. дю Сотуа,^[7]и с алгебраические методы с помощью группы когомологий Б. Эйк и К. Р. Лидхэм-Грин.^[8]Первые методы допускают качественную проницательность предельная виртуальная периодичность, последние методы определяют количественную структуру.

Теорема.Для любого бесконечного про-п группа ${ displaystyle S}$ кокласса ${ displaystyle r geq 1}$ и размер ${ displaystyle d}$, и для любой заданной глубины ${ Displaystyle к geq 1}$, существует эффективная минимальная нижняя оценка ${ Displaystyle е (к) geq 1}$,куда периодичность длины ${ displaystyle d}$ обрезанных ветвей кокосового дерева ${ Displaystyle { mathcal {T}} (S)}$ множеств, то есть существуют изоморфизмы графов

${ Displaystyle (7) qquad { mathcal {B}} _ {k} (n + d) simeq { mathcal {B}} _ {k} (n)}$ для всех ${ Displaystyle п GEQ е (к)}$.

Для доказательства щелкните Показать с правой стороны.

Эти центральные результаты могут быть выражены наглядно: если мы смотрим на коклассовое дерево через пару шаров и игнорируем конечное число предпериодических ветвей наверху, то мы увидим повторяющийся конечный образец (окончательный Однако если взять более широкие шоры, то предпериодический начальный участок может стать длиннее (виртуальный периодичность).

Вершина ${ Displaystyle P = R_ {е (к)}}$ называется периодический корень обрезанного коклассового дерева для фиксированного значения глубины ${ displaystyle k}$См. Рисунок 1.

Мультифуркационные и коклассовые графы

Предположим, что родители конечных п-группы определяются как последние нетривиальные нижние центральные факторы (P2). п-группа ${ displaystyle G}$ кокласса ${ Displaystyle mathrm {cc} (G) = r}$, мы можем выделить его (все) дочернее дерево ${ Displaystyle { mathcal {T}} (G)}$и это кокласс-${ displaystyle r}$ потомок ${ Displaystyle { mathcal {T}} ^ {r} (G)}$, то есть поддерево, состоящее из потомков кокласса ${ displaystyle r}$ только группа ${ displaystyle G}$ называется коклассовый если ${ Displaystyle { mathcal {T}} (G) = { mathcal {T}} ^ {r} (G)}$, т.е. если нет потомков ${ displaystyle G}$ с большим классом, чем ${ displaystyle r}$.

В ядерный разряд ${ Displaystyle Nu (G)}$ из ${ displaystyle G}$в теории палгоритм генерации группы М. Ф. Ньюман^[11]и Э. А. О'Брайен^[12]предоставляет следующие критерии.

N

1. ${ displaystyle G}$ является терминальным, а значит, тривиально коклассовым, тогда и только тогда, когда ${ Displaystyle Nu (G) = 0}$.
2. Если ${ Displaystyle Nu (G) = 1}$, тогда ${ displaystyle G}$ способен, но остается неизвестным, ${ displaystyle G}$ рассчитывается по коклассу.
3. Если ${ Displaystyle Nu (G) = м GEQ 2}$, тогда ${ displaystyle G}$ способна и определенно не оседает на класс.

В последнем случае возможно более точное утверждение: если ${ displaystyle G}$ имеет кокласс ${ displaystyle r}$ и ядерный разряд ${ Displaystyle Nu (G) = м GEQ 2}$, то рождает м-складная мультифуркацияв обычный кокласс-р потомок дерево ${ Displaystyle { mathcal {T}} ^ {r} (G)}$и ${ displaystyle m-1}$ нерегулярный потомок графики ${ displaystyle { mathcal {T}} ^ {r + j} (G)}$ кокласса ${ displaystyle r + j}$,за ${ Displaystyle 1 Leq J Leq м-1}$Следовательно, дерево потомков ${ displaystyle G}$ дизъюнктный союз

${ Displaystyle (8) qquad { mathcal {T}} (G) = { dot { cup}} _ {j = 0} ^ {m-1} , { mathcal {T}} ^ { г + j} (G)}$.

Мультифуркация коррелирует с разными порядками последнего нетривиального нижнего центра прямых потомков. Поскольку класс нильпотентности увеличивается ровно на единицу, ${ Displaystyle с = mathrm {cl} (Q) = mathrm {cl} (P) +1}$, от родителя ${ Displaystyle Р = Q / гамма _ {с} (Q) = pi (Q)}$ любому непосредственному потомку ${ displaystyle Q}$кокласс остается устойчивым, ${ Displaystyle г = mathrm {cc} (Q) = mathrm {cc} (P)}$, если последний нетривиальный нижний центр является циклическим порядка ${ displaystyle vert gamma _ {c} (Q) vert = p}$, так как тогда показатель порядка тоже увеличивается ровно на единицу, ${ displaystyle vert Q vert = p cdot vert P vert}$ .В этом случае, ${ displaystyle Q}$ это обычный немедленный потомок с направленным краем ${ Displaystyle P leftarrow Q}$ из размер шага ${ displaystyle 1}$, как обычно, но кокласс увеличивается на ${ displaystyle m-1}$, если ${ displaystyle vert gamma _ {c} (Q) vert = p ^ {m}}$ с ${ displaystyle m geq 2}$.Потом ${ displaystyle Q}$ называется нерегулярный немедленный потомок с направленным краем ${ Displaystyle P leftarrow Q}$ из размер шага ${ displaystyle m}$.

Если состояние размер шага ${ displaystyle 1}$ на все ориентированные ребра накладывается максимальное дерево-потомок ${ Displaystyle { mathcal {T}} (1)}$ тривиальной группы ${ displaystyle 1}$распадается на счетное бесконечное непересекающееся объединение

${ displaystyle (9) qquad { mathcal {T}} (1) = { dot { cup}} _ {r = 0} ^ { infty} , { mathcal {G}} (p, р)}$

направленных коклассовые графы ${ Displaystyle { mathcal {G}} (р, г)}$, которые скорее леса чем деревья. Точнее, упомянутые выше Теоремы кокласса подразумевают, что

${ displaystyle (10) qquad { mathcal {G}} (p, r) = left ({ dot { cup}} _ {i} , { mathcal {T}} (S_ {i} ) right) { dot { cup}} { mathcal {G}} _ {0} (p, r)}$

дизъюнктное объединениеконечно много коклассовые деревья ${ Displaystyle { mathcal {T}} (S_ {я})}$ попарно неизоморфных бесконечных про-п группы ${ displaystyle S_ {i}}$ кокласса ${ displaystyle r}$ (Теорема D) и конечный подграф ${ displaystyle { mathcal {G}} _ {0} (p, r)}$ из спорадические группы лежащий вне любого коклассового дерева.

Идентификаторы

В Малые группы Библиотека идентификаторы конечных групп, в частности конечных п-группы, представленные в виде

${ displaystyle langle { text {order}}, { text {счетное число}} rangle}$

в следующих конкретных примерах деревьев-потомков принадлежат Х. У. Бешу, Б. Эйку и Э. А. О'Брайену.^[13][14]Когда групповые порядки даны в шкале с левой стороны, как на Рисунке 2 и Рисунке 3, идентификаторы кратко обозначаются как

${ displaystyle langle { text {счетное число}} rangle}$.

В зависимости от прайма ${ displaystyle p}$, существует верхняя граница порядка групп, для которых существует идентификатор SmallGroup, например. ${ displaystyle 512 = 2 ^ {9}}$ за ${ displaystyle p = 2}$, и ${ displaystyle 2187 = 3 ^ {7}}$ за ${ displaystyle p = 3}$.Для групп более крупных заказов обозначение с обобщенные идентификаторы используется структура, напоминающая потомок. Обычный непосредственный потомок, соединенный ребром с размером шага ${ displaystyle 1}$ со своим родителем ${ displaystyle P}$, обозначается

${ displaystyle P - # 1; { text {счетное число}}}$,

и неправильный непосредственный потомок, соединенный ребром размера шага ${ displaystyle s geq 2}$ со своим родителем ${ displaystyle P}$, обозначается

${ displaystyle P - # s; { text {счетное число}}}$.

Реализации палгоритм генерации группы в системах вычислительной алгебры ЗАЗОР и Магма используйте эти обобщенные идентификаторы, которые восходят к J. A. Ascione в 1979 году.^[15]

Конкретные примеры деревьев

Во всех примерах основной родительское определение (P2) соответствует обычному нижнему центральному ряду. Случайные отличия от исходного определения (P3) в отношении нижнего показателя -п выделены центральные серии.

Coclass 0

Коклассовый граф

${ Displaystyle (11) qquad { mathcal {G}} (p, 0) = { mathcal {G}} _ {0} (p, 0)}$

конечных п-группы кокласса ${ displaystyle 0}$ не содержит коклассового дерева и, таким образом, состоит исключительно из спорадических групп, а именно тривиальная группа ${ displaystyle 1}$ и циклическая группа ${ displaystyle C_ {p}}$ порядка ${ displaystyle p}$, который является листом (но способен по младшему показателю -п центральная серия). ${ displaystyle p = 2}$ то Идентификатор SmallGroup из ${ displaystyle C_ {p}}$ является ${ Displaystyle langle 2,1 rangle}$,за ${ displaystyle p = 3}$ это ${ Displaystyle langle 3,1 rangle}$.

Рисунок 2: Граф кокласса конечных 2-групп с коклассом 1

Кокласс 1

Коклассовый граф

${ Displaystyle (12) qquad { mathcal {G}} (p, 1) = { mathcal {T}} ^ {1} (R) { dot { cup}} { mathcal {G}} _ {0} (стр, 1)}$

конечных п-группы кокласса ${ displaystyle 1}$, также называемый максимальный класс, состоит из уникальных коклассовое дерево ${ Displaystyle { mathcal {T}} ^ {1} (R)}$ с корнем ${ Displaystyle R = C_ {p} times C_ {p}}$, то элементарный абелев п-группа ранга ${ displaystyle 2}$, и один изолированная вершина(терминальный сирота без собственного родителя в том же графе кокласса, так как направленное ребро тривиальной группы ${ displaystyle 1}$ имеет размер шага ${ displaystyle 2}$), циклическая группа ${ displaystyle C_ {p ^ {2}}}$ порядка ${ displaystyle p ^ {2}}$ в спорадической части ${ displaystyle { mathcal {G}} _ {0} (p, 1)}$(однако эта группа способна по младшему показателю -п центральная серия) .Дерево ${ Displaystyle { mathcal {T}} ^ {1} (R) = { mathcal {T}} ^ {1} (S_ {1})}$ является коклассовым деревом единственного бесконечный проп группа ${ displaystyle S_ {1}}$ кокласса ${ displaystyle 1}$.

За ${ displaystyle p = 2}$, соотв. ${ displaystyle p = 3}$, идентификатор SmallGroup корневого ${ displaystyle R}$ является ${ Displaystyle langle 4,2 rangle}$, соотв. ${ Displaystyle langle 9,2 rangle}$, и древовидная диаграмма коклассового графа из ветви ${ Displaystyle { mathcal {B}} (2)}$ вниз к ветке ${ Displaystyle { mathcal {B}} (7)}$(в расчете на п-логарифм порядка корня ветви) изображен на рис.2, соответственно. Рисунок 3, где все группы порядка не менее ${ displaystyle p ^ {3}}$ находятся метабелевский, неабелева с производной длиной ${ displaystyle 2}$(вершины представлены черными кругами в отличие от контурных квадратов, обозначающих абелевы группы). На рисунке 3 меньшие черные круги обозначают метабелевы 3-группы, в которых даже максимальные подгруппы неабелевы, что не происходит для метабелевых 2-групп на рисунке 2, поскольку все они обладают абелевой подгруппой индекса ${ displaystyle p}$ (обычно ровно один). ${ Displaystyle { mathcal {G}} (2,1)}$, соотв. ${ Displaystyle { mathcal {G}} (3,1)}$, имеет периодический корень ${ Displaystyle langle 8,3 rangle}$ и периодичность длины ${ displaystyle 1}$ начиная с отделения ${ Displaystyle { mathcal {B}} (3)}$, соотв. периодический корень ${ displaystyle langle 81,9 rangle}$ и периодичность длины ${ displaystyle 2}$ установка с веткой ${ Displaystyle { mathcal {B}} (4)}$. Оба дерева имеют ветви ограниченной глубины. ${ displaystyle 1}$, так что их виртуальная периодичность на самом деле строгая периодичность.

Однако коклассовое дерево ${ Displaystyle { mathcal {G}} (р, 1)}$ с ${ displaystyle p geq 5}$ имеет безграничная глубина и содержит немабелевы группы, а коклассовое дерево ${ Displaystyle { mathcal {G}} (р, 1)}$ с ${ displaystyle p geq 7}$ имеет даже неограниченная ширина, то есть количество потомков фиксированного порядка неограниченно увеличивается с ростом порядка.^[16]

С помощью ядра и мишени переводов Artinдиаграммы на рисунках 2 и 3 могут быть снабжены дополнительной информацией и перерисованы как структурированные деревья-потомки.

Конкретные примеры ${ Displaystyle { mathcal {G}} (2,1)}$ и ${ Displaystyle { mathcal {G}} (3,1)}$ коклассового графа дают возможность дать параметризованный полициклический коммутатор мощности презентация^[17]для полного коклассового дерева ${ Displaystyle { mathcal {T}} ^ {1} (R) subset { mathcal {G}} (p, 1)}$, ${ Displaystyle р в lbrace 2,3 rbrace}$, упомянутый в ведущем разделе как преимущество концепции дерева потомков и как следствие периодичности всего коклассового дерева. В обоих случаях группа ${ Displaystyle G in { mathcal {T}} ^ {1} (R)}$ генерируется двумя элементами ${ displaystyle x, y}$но презентация содержит серию высшие коммутаторы ${ displaystyle s_ {j} = lbrack s_ {j-1}, x rbrack}$, ${ Displaystyle 3 Leq J Leq N-1 = mathrm {cl} (G)}$, начиная с главный коммутатор ${ Displaystyle s_ {2} = lbrack y, x rbrack}$Формально нильпотентность выражается соотношением ${ displaystyle s_ {n} = 1}$, когда группа в порядке ${ displaystyle vert G vert = p ^ {n}}$.

Рисунок 3: Граф кокласса конечных 3-групп с коклассом 1

За ${ displaystyle p = 2}$, есть два параметра ${ Displaystyle 0 Leq ш, г Leq 1}$ а компьютерная презентация представлена

(13)${ displaystyle { begin {align} G ^ {n} (z, w) = & langle x, y, s_ {2}, ldots, s_ {n-1} mid & x ^ {2} = s_ {n-1} ^ {w}, y ^ {2} = s_ {2} ^ {- 1} s_ {n-1} ^ {z}, lbrack s_ {2}, y rbrack = 1, & s_ {2} = lbrack y, x rbrack, s_ {j} = lbrack s_ {j-1}, x rbrack { text {for}} 3 leq j leq n -1 rangle end {выровнен}}}$

2-группы максимального класса, т.е. кокласса ${ displaystyle 1}$, форма три периодические бесконечные последовательности,

• то двугранный группы, ${ Displaystyle D (2 ^ {n}) = G ^ {n} (0,0)}$, ${ Displaystyle п geq 3}$, образуя магистраль (с бесконечно способными вершинами),
• обобщенный кватернион группы, ${ Displaystyle Q (2 ^ {n}) = G ^ {n} (0,1)}$, ${ Displaystyle п geq 3}$, которые все являются конечными вершинами,
• то полудиэдральный группы, ${ Displaystyle S (2 ^ {n}) = G ^ {n} (1,0)}$, ${ displaystyle n geq 4}$, которые также являются листьями.

За ${ displaystyle p = 3}$, есть три параметра ${ displaystyle 0 leq a leq 1}$ и ${ Displaystyle -1 Leq ш, г Leq 1}$ а компьютерная презентация представлена

(14)${ displaystyle { begin {align} G_ {a} ^ {n} (z, w) = & langle x, y, s_ {2}, ldots, s_ {n-1} mid & x ^ {3} = s_ {n-1} ^ {w}, y ^ {3} = s_ {2} ^ {- 3} s_ {3} ^ {- 1} s_ {n-1} ^ {z} , lbrack y, s_ {2} rbrack = s_ {n-1} ^ {a}, & s_ {2} = lbrack y, x rbrack, s_ {j} = lbrack s_ {j -1}, x rbrack { text {for}} 3 leq j leq n-1 rangle end {align}}}$

3 группы с параметром ${ displaystyle a = 0}$ обладают абелевой максимальной подгруппой, с параметром ${ displaystyle a = 1}$ Точнее, существующая абелева максимальная подгруппа единственна, за исключением двух особо особенный группы ${ displaystyle G_ {0} ^ {3} (0,0)}$ и ${ displaystyle G_ {0} ^ {3} (0,1)}$, где все четыре максимальные подгруппы абелевы.

В отличие от любого более крупного кокласса ${ displaystyle r geq 2}$, коклассовый граф ${ Displaystyle { mathcal {G}} (р, 1)}$ исключительно содержит п-группы ${ displaystyle G}$ с абелианизацией ${ Displaystyle G / G ^ { prime}}$ типа ${ displaystyle (p, p)}$, за исключением его единственной изолированной вершины ${ displaystyle C_ {p ^ {2}}}$Дело ${ displaystyle p = 2}$ отличается истинностью обратного утверждения: любая 2-группа с абелианизацией типа ${ displaystyle (2,2)}$ из кокласса ${ displaystyle 1}$ (Теорема О. Таусского^[18]).

Рисунок 4: Интерфейс между конечными 3-группами кокласса 1 и 2 типа (3,3)

Coclass 2

Происхождение коклассового графа ${ Displaystyle { mathcal {G}} (р, г)}$ с ${ displaystyle r geq 2}$ не является однородным.п-группы с несколькими различными абелианизациями вносят свой вклад в его состав. ${ displaystyle r = 2}$, есть существенные вклады от групп ${ displaystyle G}$ с абелианизациями ${ Displaystyle G / G ^ { prime}}$ типов${ displaystyle (p, p)}$, ${ displaystyle (p ^ {2}, p)}$, ${ displaystyle (p, p, p)}$, и изолированный вклад циклической группы ${ displaystyle C_ {p ^ {3}}}$ порядка ${ displaystyle p ^ {3}}$:

${ Displaystyle (15) qquad { mathcal {G}} (p, 2) = { mathcal {G}} _ {(p, p)} (p, 2) { dot { cup}} { mathcal {G}} _ {(p ^ {2}, p)} (p, 2) { dot { cup}} { mathcal {G}} _ {(p, p, p)} (p , 2) { dot { cup}} { mathcal {G}} _ {(p ^ {3})} (p, 2)}$.

Абелианизация типа (п,п)

В отличие от п-группы кокласса ${ displaystyle 2}$ с абелианизацией типа ${ displaystyle (p ^ {2}, p)}$ или же ${ displaystyle (p, p, p)}$, которые возникают как обычные потомки абелевых п-группы однотипных,п-группы кокласса ${ displaystyle 2}$ с абелианизацией типа ${ displaystyle (p, p)}$происходят от неправильных потомков неабелева п-группа кокласса ${ displaystyle 1}$ который не урегулирован коклассом.

Для премьер ${ displaystyle p = 2}$, таких групп вообще не существует, так как 2-группа ${ Displaystyle langle 8,3 rangle}$ кокласс установлен, что является более глубокой причиной теоремы Таусского. Этот замечательный факт был замечен Дж. Багнерой.^[19]уже в 1898 году.

Для нечетных простых чисел ${ displaystyle p geq 3}$,Существование п-группы кокласса ${ displaystyle 2}$ с абелианизацией типа ${ displaystyle (p, p)}$связано с тем, что группа ${ displaystyle G_ {0} ^ {3} (0,0)}$ не считается коклассом, его ядерный ранг равен ${ displaystyle 2}$, что приводит к бифуркация потомка дерева ${ Displaystyle { mathcal {T}} (G_ {0} ^ {3} (0,0))}$ на два коклассовых графа. ${ Displaystyle { mathcal {T}} ^ {1} (G_ {0} ^ {3} (0,0))}$является поддеревом уникального дерева ${ displaystyle { mathcal {T}} ^ {1} (C_ {p} times C_ {p})}$ в графе кокласса ${ Displaystyle { mathcal {G}} (р, 1)}$.Неправильный компонент ${ displaystyle { mathcal {T}} ^ {2} (G_ {0} ^ {3} (0,0))}$становится подграфом ${ Displaystyle { mathcal {G}} = { mathcal {G}} _ {(p, p)} (p, 2)}$ коклассового графа ${ Displaystyle { mathcal {G}} (р, 2)}$при соединении кромок шагового размера ${ displaystyle 2}$ нерегулярных прямых потомков ${ displaystyle G_ {0} ^ {3} (0,0)}$ удалены.

За ${ displaystyle p = 3}$, этот подграф ${ Displaystyle { mathcal {G}}}$ изображен на рисунке 4, который показывает границу между конечными 3-группами с коклассом ${ displaystyle 1}$ и ${ displaystyle 2}$ типа ${ Displaystyle (3,3)}$.${ Displaystyle { mathcal {G}}}$ имеет семь вершин верхнего уровня трех важных типов, каждая из которых имеет порядок ${ displaystyle 243 = 3 ^ {5}}$, которые были обнаружены Г. Баннером.^[19]

• Во-первых, есть два терминала Σ-группы Шура ${ Displaystyle langle 243,5 rangle}$ и ${ Displaystyle langle 243,7 rangle}$ в спорадической части ${ displaystyle { mathcal {G}} _ {0} (3,2)}$ коклассового графа ${ Displaystyle { mathcal {G}} (3,2)}$.
• Во-вторых, две группы ${ Displaystyle G = langle 243,4 rangle}$ и ${ Displaystyle G = langle 243,9 rangle}$ корни конечных деревьев ${ Displaystyle { mathcal {T}} ^ {2} (G)}$ в спорадической части ${ displaystyle { mathcal {G}} _ {0} (3,2)}$. Однако, поскольку они не заселены коклассом, все деревья ${ Displaystyle { mathcal {T}} (G)}$ бесконечны.
• Наконец, три группы ${ Displaystyle langle 243,3 rangle}$, ${ Displaystyle langle 243,6 rangle}$ и ${ Displaystyle langle 243,8 rangle}$ дают начало (бесконечным) коклассовым деревьям, например, ${ Displaystyle { mathcal {T}} ^ {2} ( langle 729,40 rangle)}$, ${ Displaystyle { mathcal {T}} ^ {2} ( langle 243,6 rangle)}$, ${ Displaystyle { mathcal {T}} ^ {2} ( langle 243,8 rangle)}$, каждая из которых имеет метабелеву основную линию, в графе кокласса ${ Displaystyle { mathcal {G}} (3,2)}$. Ни одна из этих трех групп не заселена по классу.

Отображая дополнительную информацию о ядрах и целях передачи Артина, мы можем нарисовать эти деревья как структурированные деревья-потомки.

Определение.Как правило, Группа Шура (называется закрыто группы И. Шура, автора концепции) является про-п группа ${ displaystyle G}$ ранг отношения ${ displaystyle d_ {2} (G) = mathrm {dim} _ { mathbb {F} _ {p}} ( mathrm {H} ^ {2} (G, mathbb {F} _ {p} ))}$ совпадает со своим рангом генератора ${ displaystyle d_ {1} (G) = mathrm {dim} _ { mathbb {F} _ {p}} ( mathrm {H} ^ {1} (G, mathbb {F} _ {p} ))}$.A σ-группа является про-п группа ${ displaystyle G}$ который обладает автоморфизмом ${ displaystyle sigma in mathrm {Aut} (G)}$индуцирование инверсии ${ Displaystyle х mapsto х ^ {- 1}}$ по его абелианизации ${ Displaystyle G / G ^ { prime}}$.A Σ-группа Шура группа Шура ${ displaystyle G}$ которая также является σ-группой и имеет конечную абелианизацию ${ Displaystyle G / G ^ { prime}}$.

${ Displaystyle langle 243,3 rangle}$ не корень коклассового дерева,

поскольку его непосредственный потомок ${ Displaystyle langle 729,40 rangle}$, который является корнем коклассового дерева с метабелевыми вершинами главной линии, имеет двух братьев и сестер ${ Displaystyle langle 729,35 rangle}$, соотв. ${ Displaystyle langle 729,34 rangle}$, которые дают начало одному, соответственно. три, коклассовое дерево (я) с неметабелевыми вершинами главной линии, имеющими циклические центры порядка ${ displaystyle 3}$и ветви значительной сложности, но, тем не менее, ограниченной глубины ${ displaystyle 5}$.

Таблица 1: Факторы групп G = G (f, g, h) ^[5]

Параметры ${ displaystyle (f, g, h)}$	Абелианизация ${ Displaystyle G / G ^ { prime}}$	Коэффициент 2-го класса ${ Displaystyle G / gamma _ {3} (G)}$	Фактор класса 3 ${ Displaystyle G / gamma _ {4} (G)}$	Коэффициент 4-го класса ${ Displaystyle G / gamma _ {5} (G)}$
${ displaystyle (0,1,0)}$	${ Displaystyle (3,3)}$	${ displaystyle langle 27,3 rangle}$	${ Displaystyle langle 243,3 rangle}$	${ Displaystyle langle 729,40 rangle}$
${ Displaystyle (0,1,2)}$	${ Displaystyle (3,3)}$	${ displaystyle langle 27,3 rangle}$	${ Displaystyle langle 243,6 rangle}$	${ Displaystyle langle 729,49 rangle}$
${ Displaystyle (1,1,2)}$	${ Displaystyle (3,3)}$	${ displaystyle langle 27,3 rangle}$	${ Displaystyle langle 243,8 rangle}$	${ Displaystyle langle 729,54 rangle}$
${ displaystyle (1,0,0)}$	${ Displaystyle (9,3)}$	${ Displaystyle langle 81,3 rangle}$	${ Displaystyle langle 243,15 rangle}$	${ Displaystyle langle 729,79 rangle}$
${ Displaystyle (0,0,1)}$	${ Displaystyle (9,3)}$	${ Displaystyle langle 81,3 rangle}$	${ Displaystyle langle 243,17 rangle}$	${ Displaystyle langle 729,84 rangle}$
${ displaystyle (0,0,0)}$	${ Displaystyle (3,3,3)}$	${ displaystyle langle 81,12 rangle}$	${ Displaystyle langle 243,53 rangle}$	${ Displaystyle langle 729,395 rangle}$

Pro-3 группы кокласса 2 с нетривиальным центром

Б. Эйк, К. Р. Лидхэм-Грин, М. Ф. Ньюман и Э. А. О'Брайен ^[5]построили семейство бесконечных про-3 групп с коклассом ${ displaystyle 2}$ имеющий нетривиальный центр порядка ${ displaystyle 3}$Члены семьи характеризуются тремя параметрами. ${ displaystyle (f, g, h)}$Их конечные факторы порождают все основные вершины с бициклическими центрами типа ${ Displaystyle (3,3)}$ шести коклассовых деревьев в коклассовом графе ${ Displaystyle { mathcal {G}} (3,2)}$Связь параметров с корнями этих шести деревьев приведена в таблице 1, диаграммы деревьев, за исключением абелианизации. ${ Displaystyle (3,3,3)}$, указаны на рисунках 4 и 5, а параметризованное представление pro-3 дается как

(16)${ displaystyle { begin {align} G (f, g, h) = & langle a, t, z mid & a ^ {3} = z ^ {f}, lbrack t, t ^ { a} rbrack = z ^ {g}, t ^ {1 + a + a ^ {2}} = z ^ {h}, & z ^ {3} = 1, lbrack z, a rbrack = 1, lbrack z, t rbrack = 1 rangle end {align}}}$

Рисунок 5: Конечные 3-группы кокласса 2 типа (9,3)

Абелианизация типа (п²,п)

За ${ displaystyle p = 3}$, верхние уровни поддерева ${ Displaystyle { mathcal {T}} ^ {2} ( langle 27,2 rangle)}$ коклассового графа ${ Displaystyle { mathcal {G}} (3,2)}$ изображены на рисунке 5. Наиболее важными вершинами этого дерева являются восемь братьев и сестер, имеющих общий родительский элемент. ${ Displaystyle langle 81,3 rangle}$, которые бывают трех важных типов.

• Во-первых, это три листа ${ Displaystyle langle 243,20 rangle}$, ${ Displaystyle langle 243,19 rangle}$, ${ Displaystyle langle 243,16 rangle}$ имеющий циклический центр порядка ${ displaystyle 9}$, и один лист ${ Displaystyle langle 243,18 rangle}$ с бициклическим центром типа ${ Displaystyle (3,3)}$.
• Во-вторых, группа ${ Displaystyle G = langle 243,14 rangle}$ является корнем конечного дерева ${ Displaystyle { mathcal {T}} (G) = { mathcal {T}} ^ {2} (G)}$.
• Наконец, три группы ${ Displaystyle langle 243,13 rangle}$, ${ Displaystyle langle 243,15 rangle}$ и ${ Displaystyle langle 243,17 rangle}$ дают начало бесконечным коклассовым деревьям, например, ${ Displaystyle { mathcal {T}} ^ {2} ( langle 2187,319 rangle)}$, ${ Displaystyle { mathcal {T}} ^ {2} ( langle 243,15 rangle)}$, ${ Displaystyle { mathcal {T}} ^ {2} ( langle 243,17 rangle)}$, каждая из которых имеет метабелеву основную линию, первая из которых имеет циклические центры порядка ${ displaystyle 3}$, второй и третий с бициклическими центрами типа ${ Displaystyle (3,3)}$.

Здесь, ${ Displaystyle langle 243,13 rangle}$ не является корнем коклассового дерева, поскольку помимо его потомка ${ Displaystyle langle 2187,319 rangle}$, которое является корнем коклассового дерева с метабелевыми вершинами основной линии, у него есть еще пять потомков, которые дают начало коклассовым деревьям с неметабелевыми вершинами основной линии, имеющими циклические центры порядка ${ displaystyle 3}$и ответвления чрезвычайной сложности, здесь частично даже с безграничная глубина.^[5]

Рисунок 6: Конечные 2-группы кокласса 2,3,4 и типа (2,2,2)

Абелианизация типа (п,п,п)

За ${ displaystyle p = 2}$, соотв. ${ displaystyle p = 3}$существует единственное коклассовое дерево с п-группы типа ${ displaystyle (p, p, p)}$ в графе кокласса ${ Displaystyle { mathcal {G}} (р, 2)}$.Его корень - элементарный абелев п-группа типа ${ displaystyle (p, p, p)}$, то есть, ${ Displaystyle langle 8,5 rangle}$, соотв. ${ displaystyle langle 27,5 rangle}$Это уникальное дерево соответствует про-2 группе семейства ${ displaystyle # 59}$ М. Ф. Ньюман и Э. А. О'Брайен,^[6]соотв. группе про-3 по параметрам ${ Displaystyle (е, г, ч) = (0,0,0)}$ в таблице 1. ${ displaystyle p = 2}$, дерево показано на рисунке 6, где показаны некоторые конечные 2-группы с коклассом ${ displaystyle 2,3,4}$ типа ${ displaystyle (2,2,2)}$.

Coclass 3

Снова здесь, п-группы с несколькими различными абелианизациями вносят свой вклад в построение коклассового графа ${ Displaystyle { mathcal {G}} (р, 3)}$.Бывают штатные, соотв. нерегулярные, существенные взносы от групп ${ displaystyle G}$ с абелианизациями ${ Displaystyle G / G ^ { prime}}$ типов${ displaystyle (p ^ {3}, p)}$, ${ displaystyle (p ^ {2}, p ^ {2})}$, ${ displaystyle (p ^ {2}, p, p)}$, ${ Displaystyle (р, р, р, р)}$, соотв. ${ displaystyle (p, p)}$, ${ displaystyle (p ^ {2}, p)}$, ${ displaystyle (p, p, p)}$, и изолированный вклад циклической группы ${ displaystyle C_ {p ^ {4}}}$ порядка ${ displaystyle p ^ {4}}$.

Абелианизация типа (п,п,п)

Поскольку элементарный абелев п-группа ${ displaystyle C_ {p} times C_ {p} times C_ {p}}$ ранга ${ displaystyle 3}$, то есть,${ Displaystyle langle 8,5 rangle}$, соотв. ${ displaystyle langle 27,5 rangle}$, за ${ displaystyle p = 2}$, соотв. ${ displaystyle p = 3}$, не оседает коклассом, а порождает мультифуркацию. ${ displaystyle { mathcal {T}} ^ {2} (C_ {p} times C_ {p} times C_ {p})}$ описан в разделе о коклассе ${ displaystyle 2}$.Неправильный компонент ${ displaystyle { mathcal {T}} ^ {3} (C_ {p} times C_ {p} times C_ {p})}$становится подграфом ${ Displaystyle { mathcal {G}} = { mathcal {G}} _ {(p, p, p)} (p, 3)}$ коклассового графа ${ Displaystyle { mathcal {G}} (р, 3)}$при соединении кромок шагового размера ${ displaystyle 2}$ нерегулярных прямых потомков ${ displaystyle C_ {p} times C_ {p} times C_ {p}}$ удалены.

За ${ displaystyle p = 2}$, этот подграф ${ Displaystyle { mathcal {G}}}$ содержится на рисунке 6, он имеет девять вершин верхнего уровня порядка ${ displaystyle 32 = 2 ^ {5}}$ которые можно разделить на конечные и способные вершины.

• Две группы ${ Displaystyle langle 32,32 rangle}$ и ${ Displaystyle langle 32,33 rangle}$ листья.
• Пять групп ${ displaystyle langle 32,27..31 rangle}$ и две группы ${ displaystyle langle 32,34..35 rangle}$ бесконечно способны.

Деревья, возникающие из способных вершин, ассоциированы с бесконечными про-2 группами М. Ф. Ньюманом и Э. А. О'Брайеном.^[6]следующим образом.

${ Displaystyle langle 32,28 rangle}$ рождает два дерева,

${ Displaystyle { mathcal {T}} ^ {3} ( langle 64,140 rangle)}$ связанный с семьей ${ displaystyle # 73}$,и

${ Displaystyle { mathcal {T}} ^ {3} ( langle 64,147 rangle)}$ связанный с семьей ${ displaystyle # 74}$.

${ Displaystyle { mathcal {T}} ^ {3} ( langle 32,29 rangle)}$ связан с семьей ${ displaystyle # 75}$.

${ Displaystyle { mathcal {T}} ^ {3} ( langle 32,30 rangle)}$ связан с семьей ${ displaystyle # 76}$.

${ Displaystyle { mathcal {T}} ^ {3} ( langle 32,31 rangle)}$ связан с семьей ${ displaystyle # 77}$.

${ Displaystyle langle 32,34 rangle}$ дает начало

${ Displaystyle { mathcal {T}} ^ {3} ( langle 64,174 rangle)}$ связанный с семьей ${ displaystyle # 78}$. Ну наконец то,