Диссипативный солитон - Dissipative soliton
Диссипативные солитоны (ДС) устойчивые уединенные локализованные структуры, возникающие в нелинейных пространственно-протяженных диссипативные системы за счет механизмов самоорганизация. Их можно рассматривать как продолжение классической солитон концепция в консервативных системах. Альтернативная терминология включает автосолитоны, пятна и импульсы.
Помимо аспектов, подобных поведению классических частиц, таких как образование связанных состояний, ДС демонстрируют интересное поведение - например, рассеяние, создание и аннигиляция - все без ограничений энергии или сохранения импульса. Возбуждение внутреннего степени свободы может привести к динамически стабилизированной собственной скорости или периодическим колебаниям формы.
Историческое развитие
Происхождение концепции солитона
ДС наблюдаются экспериментально давно. Гельмгольца[1] измерил скорость распространения нервных импульсов в 1850 году. В 1902 г. Lehmann[2] обнаружил образование локализованных анодных пятен в длинных газоразрядных трубках. Тем не менее термин «солитон» изначально разрабатывался в другом контексте. Отправной точкой стало экспериментальное обнаружение "уединенных волн на воде" Рассел в 1834 г.[3]Эти наблюдения положили начало теоретической работеРэлей[4] и Буссинеск[5] около 1870 г., что, наконец, привело к приблизительному описанию таких волн Кортевегом и де Фризом в 1895 г .; это описание известно сегодня как (консервативное)КдВ уравнение.[6]
На этом фоне термин "солитон "был придуман Забуский и Крускал[7] в 1965 г. Эти авторы исследовали некоторые хорошо локализованные уединенные решения уравнения КдФ и назвали эти объекты солитонами. Среди прочего, они продемонстрировали, что в одномерном пространстве существуют политоны, например в виде двух однонаправленно распространяющихся импульсов с разным размером и скоростью и обладающих замечательным свойством, состоящим в том, что количество, форма и размер одинаковы до и после столкновения.
Gardner et al.[8] представил метод обратной задачи рассеяния для решения уравнения КдФ и доказал, что это уравнение полностью интегрируемый. В 1972 г. Захаров иШабат[9] нашел еще одно интегрируемое уравнение и, наконец, оказалось, что метод обратной задачи рассеяния может быть успешно применен к целому классу уравнений (например,нелинейный Шредингер исинус-Гордон уравнения). С 1965 по 1975 год было достигнуто общее соглашение: оставить за собой срок солитон импульсные уединенные решения консервативных нелинейных дифференциальных уравнений в частных производных, которые могут быть решены с помощью метода обратного рассеяния.
Слабо и сильно диссипативные системы
По мере расширения знаний о классических солитонах открылась перспектива возможной технической применимости, наиболее перспективной из которых в настоящее время является передача оптических солитонов через стекловолокно с цельюпередача данных. В отличие от консервативных систем, солитоны в волокнах рассеивают энергию, и этим нельзя пренебрегать в промежуточных и длительных временных масштабах. Тем не менее, понятие классического солитона все еще можно использовать в том смысле, что на коротком временном масштабе рассеиванием энергии можно пренебречь. В промежуточном масштабе времени необходимо учитывать малые потери энергии как возмущение, а на большом масштабе амплитуда солитона будет затухать и, наконец, исчезнуть.[10]
Однако существуют различные типы систем, которые способны создавать одиночные структуры и в которых диссипация играет существенную роль для их образования и стабилизации. Хотя исследования некоторых типов этих ДС проводились в течение длительного времени (например, см. Исследование нервных импульсов, кульминацией которых стала работа Ходжкин и Хаксли[11] в 1952 г.), с 1990 г. количество исследований значительно увеличилось (см., например, [12][13][14][15]) Возможные причины - усовершенствованные экспериментальные приборы и аналитические методы, а также наличие более мощных компьютеров для численных расчетов. В настоящее время широко используется термин диссипативные солитоны для одиночных конструкций с сильнодиссипативными системами.
Экспериментальные наблюдения ДС
Сегодня DS можно найти во многих различных экспериментальных установках. Примеры включают
- Газоразрядные системы: плазма заключен в разгрузочное пространство, которое часто имеет большую боковую протяженность по сравнению с основной разгрузочной длиной. ДС возникают в виде нитей тока между электродами и были обнаружены в системах постоянного тока с высокоомным барьером,[16] Системы переменного тока с диэлектрическим барьером,[17] и как анодные пятна,[18] а также в затрудненном разряде с металлическими электродами.[19]
- Экспериментально наблюдаемые ДС в планарных газоразрядных системах постоянного тока с высокоомным барьером

Распределение усредненной плотности тока без колебательных хвостов.
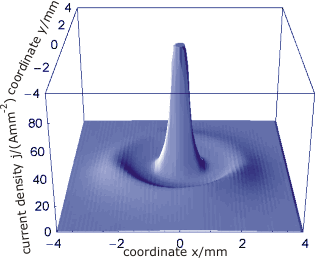
Распределение усредненной плотности тока с колебательными хвостами.
- Полупроводник системы: они похожи на газоразрядные; однако вместо газа полупроводниковый материал зажат между двумя плоскими или сферическими электродами. Установки включают Si и GaAs pin диоды,[20] n-GaAs,[21] и Si p+−n+−p − n−,[22] структуры ZnS: Mn.[23]
- Нелинейные оптические системы: световой луч высокой интенсивности взаимодействует с нелинейной средой. Обычно среда реагирует на довольно медленных временных масштабах по сравнению со временем распространения луча. Часто на выходе получается возвращен во входную систему через одинарную обратную связь или контур обратной связи. DS могут возникать как яркие пятна в двумерной плоскости, ортогональной направлению распространения луча; однако можно также использовать другие эффекты, такие как поляризация. DS наблюдались для насыщаемые поглотители,[24] выродиться оптические параметрические генераторы (ДОПО),[25] жидкокристаллический световые клапаны (LCLV),[26] системы щелочного пара,[27] фоторефрактивные среды,[28] и полупроводниковые микрорезонаторы.[29]
- Если учесть векторные свойства ДС, векторный диссипативный солитон также можно было наблюдать в волоконном лазере с пассивной синхронизацией моды через насыщающийся поглотитель,[30]
- Кроме того, был получен многоволновый диссипативный солитон в волоконном лазере с нормальной дисперсией, пассивно синхронизирующим мод с помощью SESAM. Подтверждено, что в зависимости от двулучепреломления резонатора в лазере может формироваться устойчивый одно-, двух- и трехволновый диссипативный солитон. Механизм его генерации можно проследить до природы диссипативного солитона.[31]
- Химические системы: реализованные в виде одно- и двухмерных реакторов или через каталитические поверхности, DS проявляются как импульсы (часто как распространяющиеся импульсы) повышенной концентрации или температуры. Типичные реакции: Реакция Белоусова – Жаботинского,[32] ферроцианид-йодат-сульфитная реакция, а также окисление водорода,[33] CO,[34] или утюг.[35] Нервные импульсы[11] или мигренозные волны ауры[36] тоже относятся к этому классу систем.
- Вибрирующая среда: гранулированная среда с вертикальным встряхиванием,[37] коллоидные суспензии,[38] и Ньютоновские жидкости[39] производить гармонически или субгармонически колеблющиеся груды материала, которые обычно называют осциллоны.
- Гидродинамические системы: наиболее заметной реализацией DS являются области конвекция катится по проводящему фоновому состоянию в бинарных жидкостях.[40] Другой пример - волочение пленки во вращающейся цилиндрической трубе, заполненной маслом.[41]
- Электрические сети: большие одно- или двумерные массивы связанных ячеек с нелинейным вольт-амперная характеристика.[42] DS характеризуются локально повышенным током через ячейки.
Примечательно, что феноменологически динамика ДС во многих из перечисленных выше систем схожа, несмотря на микроскопические различия. Типичными наблюдениями являются (собственное) распространение, рассеяние, формирование связанные состояния и кластеры, дрейф градиентов, взаимопроникновение, генерация и аннигиляция, а также более высокие нестабильности.
Теоретическое описание ДС
Большинство систем, показывающих ДС, описываются нелинейнымиуравнения в частных производных. Дискретно-разностные уравнения иклеточные автоматы также используются. До сих пор моделирование, основанное на первых принципах, с последующим количественным сравнением эксперимента и теории выполнялось редко и иногда также представляло серьезные проблемы из-за больших расхождений между микроскопическими и макроскопическими временными и пространственными масштабами. Часто исследуются упрощенные модели-прототипы, которые отражают основные физические процессы в более широком классе экспериментальных систем. Среди них
- Реакционно-диффузионные системы, применяется в химических системах, газовых разрядах и полупроводниках.[43] Эволюция вектора состояния q(Икс, т), описывающая концентрацию различных реагентов, определяется диффузией, а также локальными реакциями:
- Часто встречающийся пример - двухкомпонентная система активатор-ингибитор типа Фитцхью – Нагумо.
- Стационарные DS образуются за счет образования материала в центре DS, диффузионного переноса в хвосты и истощения материала в хвостах. Распространяющийся импульс возникает в результате образования на переднем конце и истощения на заднем конце.[44] Среди других эффектов - периодические колебания ДС («дыхание»),[45][46] связанные состояния,[47] и столкновения, слияние, порождение и уничтожение.[48]
- Системы типа Гинзбурга – Ландау для комплексного скаляра q(Икс, т) используется для описания нелинейных оптических систем, плазмы, конденсации Бозе-Эйнштейна, жидких кристаллов и гранулированных сред.[49] Часто встречающийся пример - кубико-квинтическое докритическое уравнение Гинзбурга – Ландау
- Чтобы понять механизмы, приводящие к образованию ДС, можно рассмотреть энергию ρ = |q|2 для которого можно вывести уравнение неразрывности
- Таким образом, можно показать, что энергия обычно вырабатывается на флангах DS и транспортируется в центр и, возможно, в хвосты, где она истощается. Динамические явления включают распространение DS в 1d,[50] распространяющиеся кластеры в 2d,[51] связанные состояния и вихревые солитоны,[52] а также «взрывающиеся ТС».[53]
- В Уравнение Свифта – Хоэнберга используется в нелинейной оптике и в динамике сыпучих сред, таких как пламя или электроконвекция. Свифта – Хоэнберга можно рассматривать как расширение уравнения Гинзбурга – Ландау. Это можно записать как
- За dр > 0 по существу имеет тот же механизм, что и в уравнении Гинзбурга – Ландау.[54] За dр <0, в реальном уравнении Свифта – Хоэнберга обнаруживается бистабильность между однородными состояниями и паттернами Тьюринга. ДС представляют собой стационарные локализованные домены Тьюринга на однородном фоне.[55] Это также верно для сложных уравнений Свифта – Хоэнберга; однако распространяющиеся DS, а также явления взаимодействия также возможны, и наблюдения включают слияние и взаимопроникновение.[56]
- Графики пространства-времени, показывающие динамику и взаимодействие DS как численные решения приведенных выше уравнений модели в одном пространственном измерении

Одиночный «дышащий» ДС как раствор двухкомпонентной реакционно-диффузионной системы с активатором. ты (левая половина) и ингибитор v (правая половина).


Свойства частиц и универсальность
ДС во многих различных системах демонстрируют универсальные свойства частиц. Чтобы понять и описать последнее, можно попытаться вывести «уравнения частиц» для медленно меняющихся параметров порядка, таких как положение, скорость или амплитуда DS, путем адиабатического исключения всех быстрых переменных в описании поля. Этот метод известен из линейных систем, однако математические проблемы возникают из нелинейных моделей из-за связи быстрых и медленных мод.[57]
Подобно низкоразмерным динамическим системам, для суперкритических бифуркаций стационарных ДС можно найти характерные нормальные формы, существенно зависящие от симметрии системы. Например, для перехода от симметричной стационарной к собственно распространяющейся ДС можно найти нормальную форму вилки
для скорости v ДП,[58] здесь σ - параметр бифуркации, а σ0точка бифуркации. Для бифуркации к «дышащей» ДС находим нормальную форму Хопфа
для амплитуды А колебания.[46] Также можно рассматривать «слабое взаимодействие», если перекрытие DS не слишком велико.[59] Таким образом упрощается сравнение эксперимента и теории.[60][61]Отметим, что указанные выше проблемы не возникают для классических солитонов, поскольку теория обратной задачи рассеяния дает полные аналитические решения.
Смотрите также
- Солитон
- Векторный солитон
- Волоконный лазер
- Нелинейная система
- Компактон, солитон с компактным носителем
- Клапотис
- Причудливые волны может быть связано с этим явлением.
- Осциллон
- Пикон, солитон с недифференцируемым пиком.
- Q-мяч нетопологический солитон
- Солитон (топологический).
- Солитон (оптика)
- Солитонная модель распространения нервного импульса
- Пространственный солитон
- Уединенные волны в дискретных средах [1]
- Топологическое квантовое число
- Уравнение синус-Гордона
- Графен
- Нелинейное уравнение Шредингера.
Рекомендации
В соответствии
- ^ Гельмгольца, Х. (1850). "Messungen über den zeitlichen Verlauf der Zuckung animalischer Muskeln und die Fortpflanzungsgeschwindigkeit der Reizung in den Nerven". Archiv für Anatomie, Physiologie und Wissenschaftliche Medicin (на немецком). 57: 276.
- ^ Леманн, О. (1902). "Gasentladungen in weiten Gefässen". Annalen der Physik (на немецком). Вайли. 312 (1): 1–28. Дои:10.1002 / andp.19013120102. ISSN 0003-3804.
- ^ J.S. Рассел, Отчет четырнадцатого заседания Британской ассоциации содействия развитию науки (1845 г.): 311
- ^ Рэлей, Дж. У. (1876 г.). «XXXII. На волнах». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. Informa UK Limited. 1 (4): 257–279. Дои:10.1080/14786447608639037. ISSN 1941-5982.
- ^ Буссинеск, Дж. (1871). "Hydrodynamique - Théorie de l'inlumescence liquide appelée onde solitaire or перевод, se propageant dans un canal rectangulaire". Comptes rendus hebdomadaires des séances de l'Académie des Sciences (На французском). 72: 755.
- ^ Кортевег, Д. Дж .; де Фрис, Г. (1895). "XLI. Об изменении формы длинных волн, наступающих в прямоугольном канале, и о новом типе длинных стационарных волн". Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. Informa UK Limited. 39 (240): 422–443. Дои:10.1080/14786449508620739. ISSN 1941-5982.
- ^ Забуски, Н. Дж .; Крускал, М. Д. (9 августа 1965 г.). «Взаимодействие« солитонов »в бесстолкновительной плазме и возвращение начальных состояний». Письма с физическими проверками. Американское физическое общество. 15 (6): 240–243. Bibcode:1965ПхРвЛ..15..240З. Дои:10.1103 / Physrevlett.15.240. ISSN 0031-9007.
- ^ Gardner, Clifford S .; Грин, Джон М .; Крускал, Мартин Д .; Миура, Роберт М. (6 ноября 1967 г.). «Метод решения уравнения Кортевега-деФриза». Письма с физическими проверками. Американское физическое общество. 19 (19): 1095–1097. Bibcode:1967ПхРвЛ..19.1095Г. Дои:10.1103 / Physrevlett.19.1095. ISSN 0031-9007.
- ^ Захаров, В. Э .; Шабат, А. Б. (1975). «Схема интегрирования нелинейных уравнений математической физики методом обратной задачи рассеяния. I». Функциональный анализ и его приложения. Springer Science and Business Media. 8 (3): 226–235. Дои:10.1007 / bf01075696. ISSN 0016-2663. S2CID 120856178.
- ^ Кившарь, Ю. С .; Агравал, Г. П. (2003). Оптические солитоны: от волокон до фотонных кристаллов. Амстердам Бостон: Academic Press. ISBN 978-0-12-410590-4. OCLC 162129411.
- ^ а б Ходжкин, А.Л .; Хаксли, А. Ф. (28 августа 1952 г.). «Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве». Журнал физиологии. Вайли. 117 (4): 500–544. Дои:10.1113 / jphysiol.1952.sp004764. ISSN 0022-3751. ЧВК 1392413. PMID 12991237.
- ^ Kerner, B.S .; Осипов, В. В. (1994). Автосолитоны: новый подход к проблемам самоорганизации и турбулентности. Дордрехт Бостон: Kluwer Academic. п. 53. ISBN 978-0-7923-2816-2. OCLC 30157395.
- ^ Боде, М .; Пурвинс, Х.-Г. (1995). «Формирование закономерностей в реакционно-диффузионных системах - диссипативных солитонах в физических системах». Physica D: нелинейные явления. Elsevier BV. 86 (1–2): 53–63. Bibcode:1995 ФИД ... 86 ... 53B. Дои:10.1016 / 0167-2789 (95) 00087-к. ISSN 0167-2789.
- ^ Christov, C.I .; Веларде, М. (1995). «Диссипативные солитоны». Physica D: нелинейные явления. Elsevier BV. 86 (1–2): 323–347. Bibcode:1995 ФИД ... 86..323C. Дои:10.1016 / 0167-2789 (95) 00111-г. ISSN 0167-2789.
- ^ Ахмедиев, Наиль; Анкевич, Адриан, ред. (2005). Диссипативные солитоны. Конспект лекций по физике LNP. Конспект лекций по физике. 661. Берлин, Гейдельберг: Springer Berlin Heidelberg. Дои:10.1007 / b11728. ISBN 978-3-540-23373-2. ISSN 0075-8450.
- ^ Radehaus, Ch .; Дирксмейер, Т .; Willebrand, H .; Пурвинс, Х.-Г. (1987). «Формирование структур в газоразрядных системах с высокоомными электродами». Письма о физике A. Elsevier BV. 125 (2–3): 92–94. Bibcode:1987ФЛА..125 ... 92Р. Дои:10.1016/0375-9601(87)90128-9. ISSN 0375-9601.
- ^ Брауэр, I .; Боде, М .; Ammelt, E .; Пурвинс, Х.-Г. (1 апреля 2000 г.). «Бегущие пары пятен в периодически управляемой газоразрядной системе: коллективное движение, вызванное взаимодействием». Письма с физическими проверками. Американское физическое общество. 84 (18): 4104–4107. Bibcode:2000ПхРвЛ..84.4104Б. Дои:10.1103 / Physrevlett.84.4104. ISSN 0031-9007. PMID 10990621.
- ^ Рубенс, Сидней М .; Хендерсон, Дж. Э. (1 августа 1940 г.). «Характеристики и функция анодных пятен в тлеющих разрядах». Физический обзор. Американское физическое общество. 58 (5): 446–457. Bibcode:1940PhRv ... 58..446R. Дои:10.1103 / Physrev.58.446. ISSN 0031-899X.
- ^ Насуно, Сатору (2003). «Танцующие» атомы и «молекулы» светящихся газоразрядных пятен ». Хаос: междисциплинарный журнал нелинейной науки. Издательство AIP. 13 (3): 1010–1013. Bibcode:2003Хаос..13.1010Н. Дои:10.1063/1.1604271. ISSN 1054-1500. PMID 12946194.
- ^ Jäger, D .; Baumann, H .; Симанчик Р. (1986). «Экспериментальное наблюдение пространственных структур за счет образования токовой нити в кремниевых pin-диодах». Письма о физике A. Elsevier BV. 117 (3): 141–144. Bibcode:1986ФЛА..117..141J. Дои:10.1016/0375-9601(86)90021-6. ISSN 0375-9601.
- ^ Майер, К. М .; Parisi, J .; Хюбенер, Р. П. (1988). «Отображение самогенерируемых многонитевых токовых структур в GaAs». Zeitschrift für Physik B. Springer Science and Business Media. 71 (2): 171–178. Bibcode:1988ZPhyB..71..171M. Дои:10.1007 / bf01312786. ISSN 0722-3277. S2CID 121227300.
- ^ Niedernostheide, F.-J .; Арпс, М .; Dohmen, R .; Willebrand, H .; Пурвинс, Х.-Г. (1 июня 1992 г.). «Пространственные и пространственно-временные структуры в полупроводниковых приборах pnpn». Физика Статус Solidi B (на немецком). Вайли. 172 (1): 249–266. Bibcode:1992ПССБР.172..249Н. Дои:10.1002 / pssb.2221720123. ISSN 0370-1972.
- ^ Бил, Марк (1993). «Равномерный и нитевидный перенос в тонкопленочных электролюминесцентных устройствах на основе ZnS: Mn постоянного тока». Философский журнал B. Informa UK Limited. 68 (5): 573–594. Bibcode:1993ПМагБ..68..573Б. Дои:10.1080/13642819308220144. ISSN 1364-2812.
- ^ Тараненко, В.Б .; Сталюнас, К .; Вайс, К. О. (1 июля 1997 г.). «Пространственный солитонный лазер: локализованные структуры в лазере с насыщающимся поглотителем в самовидящемся резонаторе». Физический обзор A. Американское физическое общество. 56 (2): 1582–1591. Bibcode:1997ПхРвА..56.1582Т. Дои:10.1103 / Physreva.56.1582. ISSN 1050-2947.
- ^ Тараненко, В.Б .; Сталюнас, К .; Вайс, К. О. (14 сентября 1998 г.). «Формирование узора и локализованные структуры при вырожденном оптически параметрическом перемешивании». Письма с физическими проверками. Американское физическое общество. 81 (11): 2236–2239. Bibcode:1998ПхРвЛ..81.2236Т. Дои:10.1103 / Physrevlett.81.2236. ISSN 0031-9007.
- ^ Schreiber, A .; Thüring, B .; Kreuzer, M .; Чуди, Т. (1997). «Экспериментальное исследование уединенных структур в нелинейно-оптической системе обратной связи». Оптика Коммуникации. Elsevier BV. 136 (5–6): 415–418. Bibcode:1997OptCo.136..415S. Дои:10.1016 / с0030-4018 (96) 00722-5. ISSN 0030-4018.
- ^ Schäpers, B .; Feldmann, M .; Ackemann, T .; Ланге, W. (24 июля 2000 г.). «Взаимодействие локализованных структур в оптической системе формирования рисунка». Письма с физическими проверками. Американское физическое общество. 85 (4): 748–751. Bibcode:2000ПхРвЛ..85..748С. Дои:10.1103 / Physrevlett.85.748. ISSN 0031-9007. PMID 10991389.
- ^ Денз, Корнелия; Шваб, Майкл; Вайльнау, Карстен (2003). Формирование поперечной структуры в фоторефрактивной оптике. Тракты Спрингера в современной физике: Ergebnisse der Exakten Naturwissenschaften. Тракты Спрингера в современной физике. 188. Берлин, Гейдельберг: Springer Berlin Heidelberg. Дои:10.1007 / b13583. ISBN 978-3-540-02109-4. ISSN 0081-3869.
- ^ Барланд, Стефан; Тредичче, Хорхе Р .; Брамбилла, Массимо; Лугиато, Луиджи А .; Балле, Сальвадор; и другие. (2002). «Солитоны резонатора как пиксели в полупроводниковых микрополостях». Природа. Springer Nature. 419 (6908): 699–702. Bibcode:2002Натура 419..699Б. Дои:10.1038 / природа01049. ISSN 0028-0836. PMID 12384692. S2CID 4404010.
- ^ Zhang, H .; Tang, D. Y .; Zhao, L.M .; Wu, X .; Там, Х. Ю. (6 января 2009 г.). "Диссипативные векторные солитоны в волоконном лазере с резонатором с регулируемой дисперсией и суммарной положительной дисперсией резонатора". Оптика Экспресс. Оптическое общество. 17 (2): 455–60. Bibcode:2009OExpr..17..455Z. Дои:10.1364 / oe.17.000455. ISSN 1094-4087. PMID 19158858.
- ^ Zhang, H .; Tang, D. Y .; Wu, X .; Чжао, Л. М. (20 июля 2009 г.). "Многоволновая диссипативная солитонная работа волоконного лазера, легированного эрбием". Оптика Экспресс. Оптическое общество. 17 (15): 12692–7. arXiv:0907.1782. Bibcode:2009OExpr..1712692Z. Дои:10.1364 / oe.17.012692. ISSN 1094-4087. PMID 19654674.
- ^ Hamik, Chad T .; Манц, Никлас; Стейнбок, Оливер (2001). "Аномальная дисперсия и привлекательное импульсное взаимодействие в реакции 1,4-циклогександиона Белоусова-Жаботинского †". Журнал физической химии A. Американское химическое общество. 105 (25): 6144–6153. Дои:10.1021 / jp010270j. ISSN 1089-5639.
- ^ Lane, Samuel L .; Лусс, Дэн (8 февраля 1993 г.). «Вращающийся температурный импульс при окислении водорода на никелевом кольце». Письма с физическими проверками. Американское физическое общество. 70 (6): 830–832. Bibcode:1993ПхРвЛ..70..830Л. Дои:10.1103 / Physrevlett.70.830. ISSN 0031-9007. PMID 10054214.
- ^ Rotermund, H.H .; Jakubith, S .; von Oertzen, A .; Эртл, Г. (10 июня 1991 г.). «Солитоны в поверхностной реакции». Письма с физическими проверками. Американское физическое общество. 66 (23): 3083–3086. Bibcode:1991ПхРвЛ..66.3083Р. Дои:10.1103 / Physrevlett.66.3083. ISSN 0031-9007. PMID 10043694.
- ^ R. Suzuki, Adv. Биофиз. 9 (1976): 115
- ^ Dahlem, Markus A .; Хаджихани, Нушин (1 марта 2009 г.). Бен-Джейкоб, Эшель (ред.). «Мигрень аура: втягивающие частицы, подобные волнам в слабо восприимчивой коре головного мозга». PLOS ONE. Публичная научная библиотека. 4 (4): e5007. Bibcode:2009PLoSO ... 4.5007D. Дои:10.1371 / journal.pone.0005007. ISSN 1932-6203. ЧВК 2659426. PMID 19337363.
- ^ Umbanhowar, Paul B .; Мело, Франсиско; Суинни, Гарри Л. (1996). «Локализованные возбуждения в вертикально колеблющемся зернистом слое». Природа. Springer Nature. 382 (6594): 793–796. Bibcode:1996Натура.382..793U. Дои:10.1038 / 382793a0. ISSN 0028-0836. S2CID 4338010.
- ^ Любашевский, О .; Hamiel, Y .; Agnon, A .; Reches, Z .; Файнберг, Дж. (18 октября 1999 г.). «Осциллоны и распространяющиеся уединенные волны в вертикально вибрирующей коллоидной суспензии». Письма с физическими проверками. Американское физическое общество. 83 (16): 3190–3193. Bibcode:1999ПхРвЛ..83.3190Л. Дои:10.1103 / Physrevlett.83.3190. ISSN 0031-9007.
- ^ Любашевский, О .; Arbell, H .; Файнберг, Дж. (20 мая 1996 г.). «Диссипативные уединенные состояния в возбужденных поверхностных волнах». Письма с физическими проверками. Американское физическое общество. 76 (21): 3959–3962. Bibcode:1996ПхРвЛ..76.3959Л. Дои:10.1103 / Physrevlett.76.3959. ISSN 0031-9007. PMID 10061156.
- ^ Алерс, Гюнтер (1991). «Эксперименты с системами формирования рисунков». Physica D: нелинейные явления. Elsevier BV. 51 (1–3): 421–443. Bibcode:1991ФИД ... 51..421А. Дои:10.1016/0167-2789(91)90249-9. ISSN 0167-2789.
- ^ Melo, F .; Дуади, С. (15 ноября 1993 г.). «От уединенных волн к статическим узорам через пространственно-временную перемежаемость». Письма с физическими проверками. Американское физическое общество. 71 (20): 3283–3286. Bibcode:1993ПхРвЛ..71.3283М. Дои:10.1103 / Physrevlett.71.3283. ISSN 0031-9007. PMID 10054934.
- ^ J. Nagumo et al., Proc. Inst. Радио Энджин. Электр. 50 (1962): 2061
- ^ Purwins, H.-G .; Bödeker, H.U .; Liehr, A.W. (2004). «Диссипативные солитоны в реакционно-диффузионных системах». Диссипативные солитоны. Конспект лекций по физике. 661. Берлин, Гейдельберг: Springer Berlin Heidelberg. С. 267–308. Дои:10.1007/10928028_11. ISBN 978-3-540-23373-2.
- ^ Мерон, Эхуд (1992). «Формирование паттернов в возбудимых средах». Отчеты по физике. Elsevier BV. 218 (1): 1–66. Bibcode:1992ФР ... 218 .... 1М. Дои:10.1016 / 0370-1573 (92) 90098-к. ISSN 0370-1573.
- ^ Niedernostheide, F.-J .; Dohmen, R .; Willebrand, H .; Schulze, H.-J .; Пурвинс, Х.-Г. (1992). «Формирование структур в нелинейных физических системах с характерными электрическими свойствами». Нелинейность с беспорядком. Springer Proceedings in Physics. 67. Берлин, Гейдельберг: Springer Berlin Heidelberg. С. 282–309. Дои:10.1007/978-3-642-84774-5_29. ISBN 978-3-642-84776-9. ISSN 0930-8989.
- ^ а б Гуревич, С. В .; Амиранашвили, Ш .; Пурвинс, Х.-Г. (1 ноября 2006 г.). «Дыхание диссипативных солитонов в трехкомпонентной системе реакция-диффузия». Физический обзор E. Американское физическое общество. 74 (6): 066201. Bibcode:2006PhRvE..74f6201G. Дои:10.1103 / Physreve.74.066201. ISSN 1539-3755. PMID 17280133.
- ^ Ор-Гиль, Михал; Г. Кеврекидис, Иоаннис; Бэр, Маркус (2000). «Устойчивые связанные состояния импульсов в возбудимой среде». Physica D: нелинейные явления. Elsevier BV. 135 (1–2): 154–174. Bibcode:2000PhyD..135..154O. Дои:10.1016 / s0167-2789 (99) 00136-0. ISSN 0167-2789.
- ^ Schenk, C.P .; Ор-Гиль, М .; Боде, М .; Пурвинс, Х.-Г. (12 мая 1997 г.). «Взаимодействующие импульсы в трехкомпонентных реакционно-диффузионных системах на двумерных областях». Письма с физическими проверками. Американское физическое общество. 78 (19): 3781–3784. Bibcode:1997ПхРвЛ..78.3781С. Дои:10.1103 / Physrevlett.78.3781. ISSN 0031-9007.
- ^ Арансон, Игорь С .; Крамер, Лоренц (4 февраля 2002 г.). «Мир комплексного уравнения Гинзбурга-Ландау». Обзоры современной физики. Американское физическое общество. 74 (1): 99–143. arXiv:cond-mat / 0106115. Bibcode:2002РвМП ... 74 ... 99А. Дои:10.1103 / revmodphys.74.99. ISSN 0034-6861. S2CID 53142414.
- ^ Афанасьев, В. В .; Ахмедиев, Н .; Сото-Креспо, Дж. М. (1 января 1996 г.). «Три формы локализованных решений пятого комплексного уравнения Гинзбурга-Ландау». Физический обзор E. Американское физическое общество. 53 (2): 1931–1939. Bibcode:1996PhRvE..53.1931A. Дои:10.1103 / Physreve.53.1931. ISSN 1063-651X. PMID 9964456.
- ^ Розанов, Н. Н .; Федоров, С. В .; Шацев, А. Н. (2006). «Движение кластеров слабосвязанных двумерных солитонов резонатора». Журнал экспериментальной и теоретической физики. Издательство Плеяды. 102 (4): 547–555. Bibcode:2006JETP..102..547R. Дои:10.1134 / s1063776106040030. ISSN 1063-7761. S2CID 59290663.
- ^ Красован, Л.-К .; Malomed, B.A .; Михалаче, Д. (20 декабря 2000 г.). «Устойчивые вихревые солитоны в двумерном уравнении Гинзбурга-Ландау». Физический обзор E. Американское физическое общество. 63 (1): 016605. Дои:10.1103 / Physreve.63.016605. ISSN 1063-651X. PMID 11304376.
- ^ Soto-Crespo, J.M .; Ахмедиев, Н .; Анкевич, А. (2 октября 2000 г.). «Пульсирующие, ползущие и вспыхивающие солитоны в диссипативных системах». Письма с физическими проверками. Американское физическое общество. 85 (14): 2937–2940. Bibcode:2000ПхРвЛ..85.2937С. Дои:10.1103 / Physrevlett.85.2937. HDL:10261/54305. ISSN 0031-9007. PMID 11005972.
- ^ Soto-Crespo, J.M .; Ахмедиев, Наиль (18 декабря 2002 г.). «Составные солитоны и двухимпульсная генерация в лазерах с пассивной синхронизацией мод, смоделированные комплексным уравнением Свифта-Хоэнберга пятой степени». Физический обзор E. Американское физическое общество. 66 (6): 066610. Bibcode:2002PhRvE..66f6610S. Дои:10.1103 / Physreve.66.066610. HDL:10261/60258. ISSN 1063-651X. PMID 12513432.
- ^ Сакагути, Хидэцугу; Бренд, Хельмут Р. (1996). «Устойчивые локализованные решения произвольной длины для пятого уравнения Свифта-Хоэнберга». Physica D: нелинейные явления. Elsevier BV. 97 (1–3): 274–285. Bibcode:1996 ФИД ... 97..274S. Дои:10.1016/0167-2789(96)00077-2. ISSN 0167-2789.
- ^ Сакагути, Хидэцугу; Бренд, Хельмут Р. (1998). «Локализованные образцы для пятого комплексного уравнения Свифта-Хоэнберга». Physica D: нелинейные явления. Elsevier BV. 117 (1–4): 95–105. Bibcode:1998PhyD..117 ... 95S. Дои:10.1016 / s0167-2789 (97) 00310-2. ISSN 0167-2789.
- ^ Фридрих, Рудольф (2005). "Теоретико-групповые методы в теории образования паттернов". Коллективная динамика нелинейных и неупорядоченных систем. Берлин / Гейдельберг: Springer-Verlag. стр.61–84. Дои:10.1007/3-540-26869-3_4. ISBN 3-540-21383-Х.
- ^ Боде, М. (1997). «Фронт-бифуркации в реакционно-диффузионных системах с неоднородным распределением параметров». Physica D: нелинейные явления. Elsevier BV. 106 (3–4): 270–286. Bibcode:1997PhyD..106..270B. Дои:10.1016 / с0167-2789 (97) 00050-х. ISSN 0167-2789.
- ^ Боде, М .; Liehr, A.W .; Schenk, C.P .; Пурвинс, Х.-Г. (2002). «Взаимодействие диссипативных солитонов: частицоподобное поведение локализованных структур в трехкомпонентной системе реакция-диффузия». Physica D: нелинейные явления. Elsevier BV. 161 (1–2): 45–66. Bibcode:2002PhyD..161 ... 45B. Дои:10.1016 / s0167-2789 (01) 00360-8. ISSN 0167-2789.
- ^ Bödeker, H.U .; Röttger, M.C .; Liehr, A. W .; Франк, Т. Д .; Фридрих, Р .; Пурвинс, Х.-Г. (28 мая 2003 г.). «Шумовая дрейфовая бифуркация диссипативных солитонов в планарной газоразрядной системе». Физический обзор E. Американское физическое общество. 67 (5): 056220. Bibcode:2003PhRvE..67e6220B. Дои:10.1103 / Physreve.67.056220. ISSN 1063-651X. PMID 12786263.
- ^ Bödeker, HU; Liehr, A W; Франк, Т. Д.; Фридрих, Р. Пурвинс, H-G (15 июня 2004 г.). «Измерение закона взаимодействия диссипативных солитонов». Новый журнал физики. IOP Publishing. 6 (1): 62. Bibcode:2004NJPh .... 6 ... 62B. Дои:10.1088/1367-2630/6/1/062. ISSN 1367-2630.
Книги и обзорные статьи
- Н. Ахмедиев и А. Анкевич, Диссипативные солитоны, Конспект лекций по физике, Springer, Берлин (2005)
- Н. Ахмедиев и А. Анкевич, Диссипативные солитоны: от оптики до биологии и медицины, Конспект лекций по физике, Springer, Берлин (2008)
- Х.-Г. Пурвинс и др., Успехи физики 59 (2010): 485 Дои:10.1080/00018732.2010.498228
- А. В. Лир: Диссипативные солитоны в реакционно-диффузионных системах. Механизм, динамика, взаимодействие. Том 70 серии Springer по синергетике, Springer, Berlin Heidelberg 2013, ISBN 978-3-642-31250-2












