Искажения (оптика) - Distortion (optics)

Фужеры, создающие неравномерное искажение фона

Оптическая аберрация
Расфокусировать Наклон Сферическая аберрация Астигматизм Кома Искажение Кривизна поля Пецваля Хроматическая аберрация

В геометрическая оптика, искажение это отклонение от прямолинейная проекция; проекция, в которой прямые линии сцены остаются прямыми на изображении. Это форма оптическая аберрация.

Радиальное искажение

Хотя искажения могут быть нерегулярными или следовать многим шаблонам, наиболее часто встречающиеся искажения являются радиально-симметричными или примерно такими же, возникающими из-за симметрии фотографический объектив. Эти радиальные искажения обычно можно классифицировать как бочка искажения или подушечка для иголок искажения. См. Ван Валри.^[1]

Бочка искажения В бочкообразном искажении изображение увеличение уменьшается по мере удаления от оптическая ось. Очевидный эффект - это эффект изображения, нанесенного на карту. сфера (или же бочка ). Линзы рыбий глаз, которые принимают полусферические виды, используют этот тип искажения как способ сопоставить бесконечно широкую плоскость объекта с конечной областью изображения. В зум-объектив, бочкообразное искажение появляется в середине диапазона фокусных расстояний объектива и хуже всего в широкоугольном конце диапазона.[2]

Подушкообразное искажение При подушкообразном искажении увеличение изображения увеличивается с увеличением расстояния от оптическая ось. Видимый эффект заключается в том, что линии, которые не проходят через центр изображения, изгибаются внутрь, к центру изображения, как подушечка для иголок.

Искривление усов Смесь обоих типов, иногда называемая искажение усов (искажение усов) или же сложное искажение, встречается реже, но не редко. Оно начинается как бочкообразное искажение вблизи центра изображения и постепенно превращается в подушкообразное искажение по направлению к периферии изображения, в результате чего горизонтальные линии в верхней половине кадра выглядят как руль усы.

Математически бочкообразные и подушкообразные искажения квадратичный, то есть они увеличиваются по мере квадрат расстояния от центра. В искажении усов квартика Член (степень 4) имеет важное значение: в центре доминирует бочкообразное искажение степени 2, в то время как на краю преобладает искажение степени 4 в направлении подушкообразной подушки. В принципе возможны и другие искажения - подушечка для булавок в центре и цилиндр по краю, или искажения более высокого порядка (степень 6, степень 8), - но обычно не возникают в практических объективах, а искажения более высокого порядка малы по сравнению с основным корпусом и подушечкой для булавок. последствия.

Вхождение

Смоделированная анимация эффекта глобуса (справа) по сравнению с простым панорамированием (слева)

В фотографии искажение особенно связано с зум-объективы, особенно зум-объективы с большим диапазоном, но их также можно найти в фикс-объективах и зависит от фокусного расстояния - например, Canon EF 50 мм ж/1.4 демонстрирует бочкообразное искажение на очень коротких фокусных расстояниях. Бочкообразное искажение может быть обнаружено в широкоугольных объективах и часто наблюдается на широкоугольном конце зум-объективов, тогда как подушкообразное искажение часто наблюдается в более старых или недорогих телеобъективы. Искажение усов особенно заметно на широком конце зума, с некоторыми ретрофокус линзы, а с недавних пор и зум-объективы большого диапазона, такие как Nikon 18–200 мм.

Определенное количество подушкообразных искажений часто обнаруживается с помощью визуальных оптических инструментов, например, бинокль, где служит для устранения эффект глобуса.

Радиальные искажения можно понять по их влиянию на концентрические круги, как в мишени для стрельбы из лука.

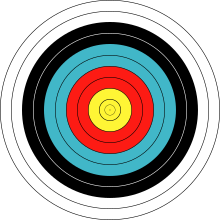
Чтобы понять эти искажения, следует помнить, что это радиальный дефекты; рассматриваемые оптические системы имеют вращательная симметрия (без нерадиальных дефектов), поэтому дидактически правильное тестовое изображение будет набором концентрический круги с равномерным разделением - как мишень стрелка. Затем можно заметить, что эти общие искажения на самом деле подразумевают нелинейное отображение радиуса от объекта к изображению: то, что на первый взгляд является подушкообразным искажением, на самом деле является просто преувеличенным отображением радиуса для больших радиусов по сравнению с маленькими. График, показывающий преобразования радиуса (от объекта к изображению), будет более крутым в верхнем (крайнем правом) конце. И наоборот, бочкообразное искажение на самом деле представляет собой отображение уменьшенного радиуса для больших радиусов по сравнению с маленькими радиусами. График, показывающий преобразования радиуса (от объекта к изображению), будет менее крутым в верхнем (крайнем правом) конце.

Хроматическая аберрация

Радиальное искажение, зависящее от длины волны, называется "боковая хроматическая аберрация "-" боковой ", потому что радиальный," хроматический ", потому что зависит от цвета (длины волны). Это может привести к появлению цветных полос в высококонтрастных областях на внешних частях изображения. Это не следует путать с осевой (продольная) хроматическая аберрация, которая вызывает аберрации по всему полю, особенно фиолетовая окантовка.

Происхождение терминов

Названия этих искажений происходят от знакомых объектов, которые визуально похожи.

• 

  При бочкообразном искажении прямые линии выпирают наружу в центре, как в бочка.

• 

  При искажении подушечками углы квадратов образуют удлиненные точки, как в подушка.

• 

  При искажении усов горизонтальные линии выступают вверх в центре, а затем изгибаются в другую сторону по мере приближения к краю кадра (если он находится в верхней части кадра), как в фигурных руль усы.

Программная коррекция

Радиальные искажения, в которых преобладают радиальные компоненты низкого порядка,^[3] можно исправить с помощью модели искажения Брауна,^[4] также известная как модель Брауна – Конради, основанная на более ранней работе Конради.^[5] Модель Брауна – Конради корректирует как радиальные, так и тангенциальные искажения, вызванные неправильным выравниванием физических элементов в объективе. Последний также известен как децентрализованное искажение. См Чжан^[6] для дополнительного обсуждения радиальной дисторсии.

${ displaystyle x _ { mathrm {u}} = x _ { mathrm {d}} + (x _ { mathrm {d}} -x _ { mathrm {c}}) (K_ {1} r ^ {2} + K_ {2} r ^ {4} + cdots) + (P_ {1} (r ^ {2} +2 (x _ { mathrm {d}} -x _ { mathrm {c}}) ^ {2 }) + 2P_ {2} (x _ { mathrm {d}} -x _ { mathrm {c}}) (y _ { mathrm {d}} -y _ { mathrm {c}})) (1 + P_ {3} r ^ {2} + P_ {4} r ^ {4} cdots)}$ ^[3]

${ displaystyle y _ { mathrm {u}} = y _ { mathrm {d}} + (y _ { mathrm {d}} -y _ { mathrm {c}}) (K_ {1} r ^ {2} + K_ {2} r ^ {4} + cdots) + (2P_ {1} (x _ { mathrm {d}} -x _ { mathrm {c}}) (y _ { mathrm {d}} -y_ { mathrm {c}}) + P_ {2} (r ^ {2} +2 (y _ { mathrm {d}} -y _ { mathrm {c}}) ^ {2})) (1 + P_ {3} r ^ {2} + P_ {4} r ^ {4} cdots),}$ ^[3]

куда:

${ Displaystyle (х _ { mathrm {d}}, y _ { mathrm {d}})}$ = точка искаженного изображения, проецируемая на плоскость изображения с использованием указанного объектива,

${ Displaystyle (х _ { mathrm {u}}, y _ { mathrm {u}})}$ = неискаженная точка изображения, проецируемая идеальным камеры-обскуры,

${ Displaystyle (х _ { mathrm {c}}, y _ { mathrm {c}})}$ = центр искажения,

${ displaystyle K_ {n}}$ = ${ Displaystyle п ^ { mathrm {th}}}$ коэффициент радиальной дисторсии,

${ displaystyle P_ {n}}$ = ${ Displaystyle п ^ { mathrm {th}}}$ коэффициент тангенциального искажения,

${ displaystyle r}$ = ${ displaystyle { sqrt {(x _ { mathrm {d}} -x _ { mathrm {c}}) ^ {2} + (y _ { mathrm {d}} -y _ { mathrm {c}}) ^ {2}}}}$, и

${ displaystyle ...}$ = бесконечная серия.

Деформация ствола обычно имеет отрицательный термин для ${ displaystyle K_ {1}}$ тогда как подушкообразное искажение будет иметь положительное значение. Искажение усов не будетмонотонный радиальный геометрическая серия где для некоторых ${ displaystyle r}$ последовательность изменит знак.

Для моделирования радиальной деформации модель деления^[7] обычно обеспечивает более точное приближение, чем полиномиальная модель четного порядка Брауна-Конради:^[8]

${ displaystyle x _ { mathrm {u}} = x _ { mathrm {c}} + { frac {x _ { mathrm {d}} -x _ { mathrm {c}}} {1 + K_ {1} г ^ {2} + К_ {2} г ^ {4} + cdots}}}$

${ displaystyle y _ { mathrm {u}} = y _ { mathrm {c}} + { frac {y _ { mathrm {d}} -y _ { mathrm {c}}} {1 + K_ {1} r ^ {2} + K_ {2} r ^ {4} + cdots}},}$ ^[7]

с использованием тех же параметров, определенных ранее. Для радиального искажения эта модель деления часто предпочтительнее модели Брауна – Конради, поскольку для более точного описания сильного искажения требуется меньше членов.^[8] При использовании этой модели для моделирования большинства камер обычно достаточно одного термина.^[9]

Программное обеспечение может исправить эти искажения с помощью искривление изображение с обратным искажением. Это включает определение того, какой искаженный пиксель соответствует каждому неискаженному пикселю, что нетривиально из-за нелинейность уравнения искажения.^[3] Боковую хроматическую аберрацию (пурпурную / зеленую окантовку) можно значительно уменьшить, применяя такое искажение отдельно для красного, зеленого и синего цветов.

Искажение или неискажение требует либо обоих наборов коэффициентов, либо обращения нелинейной задачи, которая, как правило, не имеет аналитического решения. Применяются стандартные подходы, такие как аппроксимация, локальная линеаризация и итерационные решатели. Какой решатель предпочтительнее, зависит от требуемой точности и доступных вычислительных ресурсов.

Откалиброван

Откалиброванные системы работают из таблицы передаточных функций объектива / камеры:

• Adobe Photoshop Lightroom и Photoshop CS5 могут исправить сложные искажения.
• PTlens - это плагин Photoshop или отдельное приложение, которое исправляет сложные искажения. Он не только корректирует линейные искажения, но также и нелинейные компоненты второй степени и выше.^[10]
• Lensfun это бесплатная база данных и библиотека для исправления искажения объектива.^[11]
• OpenCV - это библиотека для компьютерного зрения с открытым исходным кодом под лицензией BSD (многоязычная, много ОС). В нем есть модуль калибровки камеры.^[12]
• DxO Labs «Optics Pro может корректировать сложные искажения и учитывать фокусное расстояние.
• proDAD Defishr включает в себя инструмент Unwarp и калибратор. Из-за искажения рисунка шахматной доски рассчитывается необходимая развертка.
• В Система Micro Four Thirds камеры и объективы выполняют автоматическую коррекцию искажений с использованием параметров коррекции, которые хранятся в прошивке каждого объектива и применяются автоматически камерой и сырой конвертер программного обеспечения. Оптика большинства этих объективов имеет значительно больше искажений, чем их аналоги в системах, которые не предлагают такую ​​автоматическую коррекцию, но окончательные изображения с программной коррекцией демонстрируют заметно меньше искажений, чем у конкурирующих моделей.^[13]

Руководство

Ручные системы позволяют вручную регулировать параметры искажения:

• ImageMagick может исправить несколько искажений; например, искажение "рыбий глаз" популярной камеры GoPro Hero3 + Silver можно исправить с помощью команды^[14]

convert distorted_image.jpg -distort баррель "0,06335 -0,18432 -0,13009" corrected_image.jpg

• Фотошоп CS2 и Photoshop Elements (начиная с версии 5) включают ручной фильтр коррекции объектива для простого (подушкообразный / цилиндрический) искажения
• Corel Paint Shop Pro Фото включает в себя ручной эффект искажения линзы для простого искажения (бочкообразный, рыбий глаз, сферический "рыбий глаз" и подушкообразный).
• В GIMP включает ручную коррекцию искажения объектива (с версии 2.4).
• PhotoPerfect имеет интерактивные функции для общей настройки подушечки для булавок и для бахромы (настройка размера красной, зеленой и синей частей изображения).
• Хугин может использоваться для исправления искажений, хотя это не его основное применение.^[15]

Помимо этих систем, которые обращаются к изображениям, есть системы, которые также регулируют параметры искажения для видео:

• FFMPEG с помощью видеофильтра "линзокоррекция". ^[16]
• Блендер используя редактор узлов, чтобы вставить узел «Искажение / искажение линзы» между узлами ввода и вывода.

Связанные явления

Радиальная дисторсия - это неспособность линзы прямолинейный: невозможность изображения линий в линии. Если фотография не сделана прямо, то даже с идеальным прямолинейным объективом прямоугольники будут выглядеть как трапеции: линии отображаются как линии, но углы между ними не сохраняются (наклон не является конформная карта ). Этот эффект можно контролировать, используя линза управления перспективой, или же исправлено в постобработке.

Из-за перспектива, камеры отображают куб в виде квадрата усеченный (усеченная пирамида с трапециевидными сторонами) - дальний конец меньше ближнего. Это создает перспективу, а скорость, с которой происходит это масштабирование (насколько быстро сжимаются более удаленные объекты), создает ощущение глубины или мелкости сцены. Это не может быть изменено или исправлено простым преобразованием результирующего изображения, поскольку для этого требуется трехмерная информация, а именно глубина объектов в сцене. Этот эффект известен как перспективное искажение; само изображение не искажается, но воспринимается как искаженное при просмотре с нормального расстояния просмотра.

Обратите внимание, что если центр изображения находится ближе, чем края (например, снимок лица прямо), то бочкообразное искажение и широкоугольное искажение (при съемке с близкого расстояния) увеличивают размер центра, в то время как подушкообразное искажение и искажение телефото (съемка издалека) уменьшают размер центра. Однако радиальное искажение изгибает прямые линии (наружу или внутрь), в то время как перспективное искажение не изгибает линии, и это разные явления. Линзы рыбий глаз широкоугольные объективы с сильным бочкообразным искажением и, таким образом, демонстрируют обе эти явления, поэтому объекты в центре изображения (если они сняты с близкого расстояния) особенно увеличиваются: даже если бочкообразное искажение исправлено, результирующее изображение все равно получено широкоугольным объективом и все равно будет иметь широкоугольный угол перспективы.

Смотрите также

• Анаморфоз
• Угол обзора
• Цилиндрическая перспектива
• Искажение
• Текстурный градиент
• Подводное зрение
• Виньетирование

Рекомендации

внешняя ссылка

• Оценка и коррекция искажения объектива с исходным кодом и онлайн-демонстрацией
• Коррекция искажения объектива при постобработке
• 3D-моделирование Искажение объектива и поле зрения камеры при проектировании систем видеонаблюдения