Оптическая аберрация - Википедия - Optical aberration

Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) Эта статья в значительной степени основан на статье, не защищенной авторским правом Британская энциклопедия Одиннадцатое издание, который был произведен в 1911 году. Его следует обновить, чтобы отразить последующую историю или ученость (включая ссылки, если таковые имеются). Когда вы завершите обзор, замените это примечание простым примечанием на странице обсуждения этой статьи. (Май 2016) Эта статья может потребоваться переписан соответствовать требованиям Википедии стандарты качества. Ты можешь помочь. В страница обсуждения может содержать предложения. (Май 2009 г.) Эта статья читается как учебник и может потребовать уборка. Пожалуйста помоги чтобы улучшить эту статью сделать это нейтральный в тон и познакомьтесь с Википедией стандарты качества. (Октябрь 2020) (Узнайте, как и когда удалить этот шаблон сообщения)

Оптическая аберрация
Расфокусировать Наклон Сферическая аберрация Астигматизм Кома Искажение Кривизна поля Пецваля Хроматическая аберрация

В оптика, аберрация это свойство оптических систем, таких как линзы что вызывает свет быть распределенным по некоторой области пространства, а не сосредоточенным в какой-то точке.^[1] Аберрации приводят к размытию или искажению изображения, сформированного линзой, причем характер искажения зависит от типа аберрации. Аберрацию можно определить как отклонение характеристик оптической системы от предсказаний параксиальная оптика.^[2] В системе формирования изображений это происходит, когда свет из одной точки объекта не сходится (или не расходится) в одной точке после прохождения через систему. Аберрации возникают из-за того, что простая параксиальная теория не является полностью точной моделью воздействия оптической системы на свет, а не из-за дефектов в оптических элементах.^[3]

Оптическая система формирования изображения с аберрацией создает нечеткое изображение. Создатели оптические инструменты необходимо исправить оптические системы, чтобы компенсировать аберрации.

Аберрацию можно проанализировать с помощью методов геометрическая оптика. Статьи о отражение, преломление и каустика обсудить общие характеристики отраженного и преломленного лучи.

Обзор

Отражение от сферического зеркала. Падающие лучи (красные) от центра зеркала производят отраженные лучи (зеленые), которые не попадают в точку фокусировки F. Это происходит из-за сферическая аберрация.

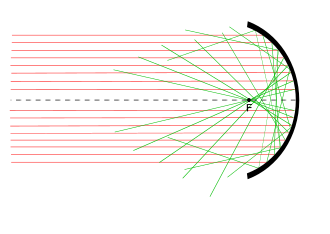
С идеальным линза свет из любой точки на объекте будет проходить через линзу и собираться в одной точке плоскость изображения (или, в более общем смысле, поверхность изображения). Однако настоящие линзы не фокусируют свет точно в одну точку, даже если они идеально сделаны. Эти отклонения от идеализированных характеристик объектива называются аберрации линзы.

Аберрации делятся на два класса: монохромный и хроматический. Монохроматические аберрации вызваны геометрией линзы или зеркала и возникают как при отражении света, так и при его преломлении. Они появляются даже при использовании монохроматический свет, отсюда и название.

Хроматические аберрации вызваны разброс, изменение линзы показатель преломления с длина волны. Из-за дисперсии световые волны различной длины фокусируются в разных точках. Хроматическая аберрация не появляется при использовании монохроматического света.

Монохроматические аберрации

Наиболее распространенные монохроматические аберрации:

• Расфокусировать
• Сферическая аберрация
• Кома
• Астигматизм
• Кривизна поля
• Искажение изображения

Хотя расфокусировка технически является оптической аберрацией самого низкого порядка, она обычно не рассматривается как аберрация линзы, поскольку ее можно исправить, перемещая линзу (или плоскость изображения), чтобы привести плоскость изображения к оптическому фокусу линзы. .

Помимо этих аберраций, поршень и наклон это эффекты, которые меняют положение фокуса. Поршень и наклон не являются истинными оптическими аберрациями, поскольку, когда идеальный волновой фронт изменяется из-за поршня и наклона, он по-прежнему будет формировать идеальное изображение без аберраций, только смещенное в другое положение.

Хроматические аберрации

Сравнение идеального изображения кольца (1) и изображений только с осевой (2) и только поперечной (3) хроматической аберрацией

Хроматическая аберрация возникает, когда разные длины волн не фокусируются в одной и той же точке. Типы хроматической аберрации:

• Осевая (или «продольная») хроматическая аберрация
• Боковая (или «поперечная») хроматическая аберрация

Теория монохроматической аберрации

В совершенной оптической системе в классическая теория оптики,^[4] лучи света исходящие от любого точка объекта объединиться в точка изображения; и поэтому объектное пространство воспроизводится в пространство изображения. Введение простых вспомогательных терминов в связи с Гаусс,^[5][6] назвал фокусные расстояния и фокальные плоскости, позволяет определять изображение любого объекта для любой системы. Однако теория Гаусса верна только до тех пор, пока углы, составляющие все лучи с оптической осью (симметричной осью системы), бесконечно малы, т.е.. с бесконечно малыми объектами, изображениями и линзами; на практике эти условия могут быть не реализованы, и изображения, проецируемые неисправленными системами, в целом, нечеткие и часто размытые, если апертура или поле зрения выходят за определенные пределы.^[6]

Исследования Джеймс Клерк Максвелл^[7] и Эрнст Аббе^[8] показали, что свойства этих репродукций, т.е.. относительное положение и величина изображений не являются особыми свойствами оптических систем, а являются необходимыми следствиями предположения (согласно Аббе) о воспроизведении всех точек пространства в точках изображения и не зависят от способа воспроизведения осуществляется. Однако эти авторы показали, что никакая оптическая система не может оправдать эти предположения, поскольку они противоречат фундаментальным законам отражения и преломления. Следовательно, теория Гаусса предоставляет только удобный метод приближения реальности; реалистичные оптические системы не соответствуют этому недостижимому идеалу. В настоящее время все, что можно сделать, - это проецировать одну плоскость на другую; но даже в этом случае всегда возникают аберрации, и маловероятно, что они когда-либо будут полностью исправлены.^[6]

Аберрация осевых точек (сферическая аберрация в узком смысле)

Рисунок 1

Пусть S (рис. 1) - произвольная оптическая система, лучи, идущие из точки оси O под углом u1, объединятся в точке оси O'1; и под углом u2 в точке оси O'2. Если есть рефракция на коллективной сферической поверхности или через тонкую положительную линзу, O'2 будет лежать перед O'1, пока угол u2 больше, чем u1 (под исправлением); и наоборот с диспергирующей поверхностью или линзами (над исправлением). Каустика в первом случае напоминает знак> (больше); во втором <(меньше чем). Если угол u1 очень мал, O'1 - гауссово изображение; и O'1 O'2 называется продольная аберрация, и O'1R боковая аберрация из карандаши с апертурой u2. Если карандаш с углом u2 является карандашом максимальной аберрации всех пропущенных карандашей, то в плоскости, перпендикулярной оси в точке O'1, имеется круговая диск замешательства радиуса O'1R, а в параллельной плоскости в точке O'2 - другого радиуса O'2R2; между этими двумя находится диск наименьшей путаницы.^[6]

Самое большое отверстие карандашей, участвующих в воспроизведении О, т.е.. угол u обычно определяется краем одной из линз или отверстием в тонкой пластине, расположенной между, перед или позади линз системы. Это отверстие называется остановка или же диафрагма; Аббе использовал термин отверстие остановка как для отверстия, так и для ограничивающего поля линзы. Компонент S1 системы, расположенный между диафрагмой и объектом O, проецирует изображение диафрагмы, названное Аббе диафрагмой. вступительный ученик; то выпускной ученик - изображение, сформированное компонентом S2, который расположен за ограничителем диафрагмы. Все лучи, выходящие из точки O и проходящие через диафрагму, также проходят через входной и выходной зрачки, так как это изображения диафрагмы. Поскольку максимальная апертура карандашей, выходящих из точки O, представляет собой угол u, который образует входной зрачок в этой точке, величина аберрации будет определяться положением и диаметром входного зрачка. Если система полностью находится за диафрагмой, то это сам входной зрачок (передняя остановка); если полностью впереди, это выходной зрачок (обратная остановка).^[6]

Если точка объекта находится на бесконечно удаленном расстоянии, все лучи, полученные первым членом системы, параллельны, и их пересечения после пересечения системы меняются в зависимости от их перпендикулярная высота падения, т.е. их расстояние от оси. Это расстояние заменяет угол u в предыдущих рассуждениях; и диафрагма, т.е.. радиус входного зрачка - его максимальное значение.^[6]

Аберрация элементов, то есть мельчайшие объекты, расположенные под прямым углом к ​​оси

Если лучи, исходящие из точки O (рис. 1), совпадают, из этого не следует, что точки в части плоскости, перпендикулярной оси O к оси, также будут совпадать, даже если часть плоскости очень мала. По мере увеличения диаметра линзы (т.е., с увеличением апертуры) соседняя точка N будет воспроизводиться, но с аберрациями, сравнимыми по величине с ON. Этих аберраций можно избежать, если, по словам Аббе, условие синуса, sin u'1 / sin u1 = sin u'2 / sin u2, выполняется для всех лучей, воспроизводящих точку O. Если точка объекта O бесконечно удалена, u1 и u2 должны быть заменены на h1 и h2, перпендикулярные высоты заболеваемость; то условие синуса тогда становится sin u'1 / h1 = sin u'2 / h2. Система, удовлетворяющая этому условию и свободная от сферической аберрации, называется апланатический (Греч. А-, приватив, планировать, блуждание). Это слово впервые употребил Роберт Блэр чтобы охарактеризовать высший ахроматизм, а впоследствии многие авторы также обозначили свободу от сферической аберрации.^[6]

Поскольку аберрация увеличивается с увеличением расстояния луча от центра линзы, аберрация увеличивается с увеличением диаметра линзы (или, соответственно, с увеличением диаметра апертуры), и, следовательно, может быть минимизирована за счет уменьшения апертуры на стоимость также уменьшения количества света, достигающего плоскости изображения.

Аберрация боковых точек объекта (точек за осью) узкими карандашами - астигматизм

фигура 2

Точка O (рис. 2) на конечном расстоянии от оси (или с бесконечно удаленным объектом, точка, которая образует конечный угол в системе), как правило, даже в этом случае не воспроизводится резко, если пучок лучей от него и обходная система делается бесконечно узкой за счет уменьшения диафрагмы; такой карандаш состоит из лучей, которые могут проходить от точки объекта через теперь уже бесконечно маленький входной зрачок. Видно (без учета исключительных случаев), что карандаш не встречается с преломляющей или отражающей поверхностью под прямым углом; следовательно, это астигматизм (греч. a-, привативный, стигмия, точка). Называя центральный луч, проходящий через входной зрачок, ось карандаша или же главный луч можно сказать: лучи карандаша пересекаются не в одной точке, а в двух фокусных линиях, которые, как можно предположить, лежат под прямым углом к ​​главному лучу; из них один лежит в плоскости, содержащей главный луч и ось системы, т.е. первая основная секция или же меридиональный разрез, а другой - под прямым углом к ​​нему, то есть во втором основном или сагиттальном сечении. Следовательно, мы не получаем ни в одной плоскости перехвата за системой, как, например, фокусирующий экран, изображение точки объекта; с другой стороны, в каждой из двух плоскостей отдельно образуются прямые O 'и O "(в соседних плоскостях образуются эллипсы), а в плоскости между O' и O" - круг наименьшего смешения. Интервал O'O ", называемый астигматической разностью, увеличивается, как правило, с увеличением угла W между главным лучом OP и осью системы, то есть с полем зрения. поверхности астигматического изображения соответствуют одной объектной плоскости; и они соприкасаются в точке оси; на одной лежат фокусные линии первого вида, на другой - второго. Системы, в которых две астигматические поверхности совпадают, называются анастигматическими или стигматическими.^[6]

Сэр Исаак Ньютон вероятно был первооткрывателем астигмации; положение линий астигматического изображения определил Томас Янг;^[9] и теория была разработана Аллвар Гуллстранд.^[10][11][6] Библиография П. Кульманна приведена в книге Морица фон Рора. Die Bilderzeugung in optischen Instrumenten.^[12][6]

Аберрация боковых точек предмета широкими карандашами - кома

При более широком открытии упора для боковых точек возникают такие же отклонения, как уже обсуждалось для осевых точек; но в этом случае они намного сложнее. Направление лучей в меридиональном сечении больше не симметрично главному лучу карандаша; а на плоскости пересечения вместо светящейся точки появляется пятно света, несимметричное относительно точки и часто проявляющее сходство с кометой, хвост которой направлен к оси или от нее. От этого внешнего вида он получил свое название. Несимметричная форма меридионального карандаша, который ранее рассматривался только как кома только в более узком смысле; другие ошибки комы были обработаны Артур Кениг и Мориц фон Рор,^[12] и позже Аллваром Гуллстрандом.^[11][6]

Кривизна поля изображения

Если вышеупомянутые ошибки будут устранены, две астигматические поверхности объединятся и резкое изображение будет получено с широкой апертурой - остается необходимость корректировать кривизну поверхности изображения, особенно когда изображение должно быть получено на плоской поверхности, например в фотографии. В большинстве случаев поверхность вогнута по направлению к системе.^[6]

Искажение изображения

Рис. 3a: Бочкообразное искажение

Рис. 3b: Подушкообразное искажение

Даже если изображение резкое, оно может быть искажено по сравнению с идеальным точечная проекция. В проекции точечного отверстия увеличение объекта обратно пропорционально его расстоянию до камеры вдоль оптической оси, так что камера, направленная прямо на плоскую поверхность, воспроизводит эту плоскую поверхность. Искажение можно рассматривать как неравномерное растяжение изображения или, что то же самое, как изменение увеличения по полю. В то время как «искажение» может включать произвольную деформацию изображения, наиболее выраженным типом искажения, создаваемым обычной оптикой формирования изображений, является «бочкообразное искажение», при котором центр изображения увеличивается больше, чем периметр (рисунок 3a). Реверс, на котором периметр увеличен больше, чем центр, известен как «подушкообразная деформация» (рис. 3b). Этот эффект называется искажением объектива или искажение изображения, и здесь алгоритмы чтобы исправить это.

Системы без искажений называются ортоскопический (ортопеды, справа, копеин смотреть) или прямолинейный (прямые линии).

Рисунок 4

Эта аберрация совершенно отличается от резкости воспроизведения; при нерезком воспроизведении вопрос об искажении возникает, если на рисунке можно распознать только части объекта. Если на нерезком изображении пятно света соответствует точке объекта, центр гравитации патч может рассматриваться как точка изображения, это точка, где плоскость, принимающая изображение, например фокусирующий экран, пересекает луч, проходящий через середину упора. Это предположение оправдано, если плохое изображение на фокусировочном экране остается неподвижным при уменьшении диафрагмы; на практике это обычно происходит. Этот луч, названный Аббе главный луч (не путать с главные лучи теории Гаусса), проходит через центр входного зрачка до первого преломления и центр выходного зрачка после последнего преломления. Из этого следует, что правильность рисования зависит исключительно от главных лучей; и не зависит от резкости или кривизны поля изображения. Ссылаясь на рис. 4 имеем O'Q '/ OQ = a' tan w '/ a tan w = 1 / N, где N - шкала или увеличение изображения. Для того чтобы N было постоянным для всех значений w, «tan w» / a tan w также должны быть постоянными. Если отношение a '/ a достаточно постоянное, как это часто бывает, указанное выше соотношение сводится к состояние Воздушный, т.е. tan w '/ tan w = константа. Это простое соотношение (см. Camb. Phil. Trans., 1830, 3, p. 1) выполняется во всех системах, симметричных относительно своей диафрагмы (кратко названных симметричные или голосимметричные объективы), или состоящие из двух одинаковых, но разных по размеру компонентов, размещенных от диафрагмы пропорционально их размеру и имеющих одинаковую кривизну (полусимметричные объективы); в этих системах tan w '/ tan w = 1.^[6]

Постоянство a '/ a, необходимое для сохранения этой связи, было указано Р. Х. Боу (Brit. Journ. Photog., 1861) и Томасом Саттоном (Photographic Notes, 1862); его рассматривали О. Люммер и М. фон Рор (Zeit. f. Instrumentenk., 1897, 17 и 1898, 18, стр. 4). Это требует, чтобы середина диафрагмы воспроизводилась в центрах входного и выходного зрачков без сферической аберрации. М. фон Рор показал, что для систем, не удовлетворяющих ни условию Эйри, ни условию Боу-Саттона, отношение a 'cos w' / a tan w будет постоянным на одном расстоянии от объекта. Это комбинированное условие точно выполняется голосимметричными объективами, воспроизводящими масштаб 1, и полусимметричными, если масштаб воспроизведения равен отношению размеров двух компонентов.^[6]

Модель аберраций Цернике

Круговые профили волнового фронта, связанные с аберрациями, могут быть математически смоделированы с использованием Многочлены Цернике. Разработан Фриц Зернике в 1930-е годы многочлены Цернике ортогональный по кругу единичного радиуса. Сложный аберрированный профиль волнового фронта может быть подогнанный по кривой с полиномами Цернике, чтобы получить набор подходящих коэффициенты которые по отдельности представляют различные типы аберраций. Эти коэффициенты Цернике равны линейно независимый, таким образом, вклад отдельных аберраций в общий волновой фронт может быть выделен и количественно определен отдельно.

Есть четный и нечетный Многочлены Цернике. Четные полиномы Цернике определяются как

${ Displaystyle Z_ {n} ^ {m} ( rho, phi) = R_ {n} ^ {m} ( rho) , cos (m , phi) !}$

и нечетные полиномы Цернике в виде

${ Displaystyle Z_ {n} ^ {- m} ( rho, phi) = R_ {n} ^ {m} ( rho) , sin (m , phi), !}$

куда м и п неотрицательны целые числа с ${ displaystyle n geq m}$, Φ - азимутальный угол в радианы, ρ - нормированное радиальное расстояние. Радиальные многочлены ${ displaystyle R_ {n} ^ {m}}$ не имеют азимутальной зависимости и определяются как

${ displaystyle R_ {n} ^ {m} ( rho) = ! sum _ {k = 0} ^ {(nm) / 2} ! ! ! { frac {(-1) ^ { k} , (nk)!} {k! , ((n + m) / 2-k)! , ((nm) / 2-k)!}} ; rho ^ {n-2 , k} quad { mbox {if}} nm { mbox {четно}}}$

и ${ Displaystyle R_ {n} ^ {m} ( rho) = 0}$ если ${ displaystyle n-m}$ странно.

Первые несколько полиномов Цернике, умноженные на соответствующие им коэффициенты подгонки, равны^[13]:

${ displaystyle a_ {0} times 1}$	«Поршень», равный среднее значение волнового фронта
${ Displaystyle а_ {1} раз ро соз ( фи)}$	«X-Tilt», отклонение габаритного луча в сагиттальный направление
${ Displaystyle а_ {2} раз ро грех ( фи)}$	«Y-Tilt», отклонение общего луча в тангенциальный направление
${ displaystyle a_ {3} times (2 rho ^ {2} -1)}$	«Расфокус», а параболический волновой фронт в результате не в фокусе
${ Displaystyle а_ {4} раз ро ^ {2} соз (2 фи)}$	«Астигматизм 0 °», a цилиндрический форма по оси X или Y
${ displaystyle a_ {5} times rho ^ {2} sin (2 phi)}$	«Астигматизм 45 °», цилиндрическая форма, ориентированная под углом ± 45 ° от оси X
${ Displaystyle а_ {6} раз (3 ро ^ {2} -2) ро соз ( фи)}$	«Икс-кома», коматическое изображение, вспыхивающее в горизонтальном направлении.
${ displaystyle a_ {7} times (3 rho ^ {2} -2) rho sin ( phi)}$	"Y-Coma", коматическое изображение, вспыхивающее в вертикальном направлении
${ displaystyle a_ {8} times (6 rho ^ {4} -6 rho ^ {2} +1)}$	«Сферическая аберрация третьего порядка»

куда ${ displaystyle rho}$ - нормализованный радиус зрачка с ${ Displaystyle 0 Leq Rho Leq 1}$, ${ displaystyle phi}$ азимутальный угол вокруг зрачка с ${ displaystyle 0 leq phi leq 2 pi}$, а подгоночные коэффициенты ${ displaystyle a_ {0}, ldots, a_ {8}}$ - ошибки волнового фронта по длинам волн.

Как в Фурье синтез с использованием синусы и косинусы, волновой фронт может быть идеально представлен достаточно большим числом полиномов Цернике высшего порядка. Однако волновые фронты с очень крутыми градиенты или очень высокий пространственная частота структура, например, произведенная распространение через атмосферная турбулентность или же аэродинамические поля течения, плохо моделируются полиномами Цернике, которые имеют тенденцию фильтр нижних частот отлично пространственный определение в волновом фронте. В этом случае другие методы подгонки, такие как фракталы или же разложение по сингулярным числам может улучшить результаты подгонки.

В круговые многочлены были представлены Фриц Зернике для оценки точечного изображения аберрированной оптической системы с учетом эффектов дифракция. Идеальное точечное изображение при наличии дифракции уже было описано Воздушный еще в 1835 году. Потребовалось почти сто лет, чтобы прийти к всеобъемлющей теории и моделировать точечный образ аберрированных систем (Зернике и Ниджбоер). Анализ Nijboer и Zernike описывает распределение интенсивности, близкое к оптимальной фокальной плоскости. Недавно была разработана расширенная теория, которая позволяет рассчитывать амплитуду и интенсивность точечного изображения в гораздо большем объеме в фокальной области (Расширенная теория Ниджбора-Зернике ). Эта расширенная теория точечного изображения Ниджбора-Цернике или формирования «функции рассеяния точки» нашла применение в общих исследованиях формирования изображений, особенно для систем с высоким числовая апертура, и в характеристике оптических систем в отношении их аберраций.^[14]

Аналитическая обработка аберраций

Предыдущий обзор нескольких ошибок воспроизведения принадлежит Теория аберраций Аббе, в котором определенные аберрации обсуждаются отдельно; он хорошо подходит для практических нужд, поскольку при создании оптического прибора стараются устранить определенные ошибки, выбор которых оправдан опытом. Однако в математическом смысле этот выбор произвольный; воспроизведение конечного объекта с конечной апертурой, по всей вероятности, влечет за собой бесконечное количество аберраций. Это число конечно только в том случае, если предполагается, что объект и апертура бесконечно малая определенного порядка; и с каждым порядком бесконечной малости, то есть с каждой степенью приближения к реальности (к конечным объектам и отверстиям), связано определенное количество аберраций. Эта связь обеспечивается только теориями, которые рассматривают аберрации в целом и аналитически с помощью неопределенных рядов.^[6]

Рисунок 5

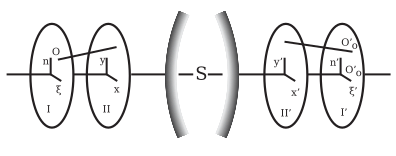
Луч, исходящий из точки O объекта (рис. 5), можно определить координатами (ξ, η). Из этой точки O на плоскости объекта I, перпендикулярной оси, и двух других координат (x, y), точка, в которой луч пересекает входной зрачок, то есть плоскость II. Аналогичным образом соответствующий луч изображения может быть определен точками (ξ ', η') и (x ', y') в плоскостях I 'и II'. Начало этих четырех плоских систем координат может быть коллинеарно оси оптической системы; и соответствующие оси могут быть параллельны. Каждая из четырех координат ξ ', η', x ', y' является функцией ξ, η, x, y; и если предположить, что поле зрения и отверстие бесконечно малы, то ξ, η, x, y имеют один и тот же порядок бесконечно малых; следовательно, разлагая ξ ', η', x ', y' по возрастанию степеней ξ, η, x, y, получаются ряды, в которых необходимо рассматривать только младшие степени. Легко видеть, что если оптическая система симметрична, начала систем координат коллинеарны оптической оси, а соответствующие оси параллельны, то при изменении знаков ξ, η, x, y значения ξ ', η' , x ', y' должны также изменить свой знак, но сохранить свои арифметические значения; это означает, что ряды ограничиваются нечетными степенями неотмеченных переменных.^[6]

Характер воспроизведения состоит в том, что лучи, исходящие из точки O, соединяются в другой точке O '; в общем, это не так, поскольку ξ ', η' меняются, если ξ, η постоянны, а x, y - переменные. Можно предположить, что плоскости I 'и II' нарисованы там, где изображения плоскостей I и II образованы лучами вблизи оси по обычным правилам Гаусса; и в результате расширения этих правил, но не соответствующего реальности, точка изображения Гаусса O '₀, с координатами ξ '₀, η '₀, точки O на некотором расстоянии от оси можно было построить. Запись Dξ '= ξ'-ξ'₀ и Dη '= η'-η'₀, то Dξ 'и Dη' являются аберрациями, принадлежащими ξ, η и x, y, и являются функциями этих величин, которые при последовательном разложении содержат только нечетные степени по тем же причинам, что указаны выше. Из-за аберраций всех лучей, проходящих через точку O, в плоскости I 'образуется пятно света, размер которого зависит от наименьших степеней ξ, η, x, y, содержащихся в аберрациях. Эти степени, названные Я. Петцваль (Bericht uber die Ergebnisse einiger dioptrischer Untersuchungen, Buda Pesth, 1843; Акад. Sitzber., Вена, 1857 г., т. xxiv. XXVI.) порядковые номера изображения, следовательно, являются лишь нечетными полномочиями; условием формирования образа m-го порядка является то, что в рядах для Dξ 'и Dη' коэффициенты при степенях 3-й, 5-й ... (m-2) -й степени должны обращаться в нуль. Поскольку изображения теории Гаусса относятся к третьему порядку, следующая задача состоит в том, чтобы получить изображение 5-го порядка или сделать коэффициенты при степенях 3-й степени равными нулю. Это требует выполнения пяти уравнений; другими словами, имеется пять изменений 3-го порядка, исчезновение которых дает изображение 5-го порядка.^[6]

Выражение для этих коэффициентов через константы оптической системы, то есть радиусы, толщины, показатели преломления и расстояния между линзами, было решено с помощью Л. Зайдель (Astr. Nach., 1856, с. 289); В 1840 г. Я. Петцваль построил свой портретный объектив на основе аналогичных расчетов, которые никогда не публиковались (см. M. von Rohr, Theorie und Geschichte des Photography Objectivs, Берлин, 1899 г., стр. 248). Теория была разработана С. Финтерсвальдером (Munchen. Acad. Abhandl., 1891, 17, p. 519), который также опубликовал посмертную статью Зайделя, содержащую краткий обзор его работы (München. Акад. Sitzber., 1898, 28, с. 395); более простая форма была дана А. Кербером (Beiträge zur Dioptrik, Лейпциг, 1895-6-7-8-9). А. Кониг и М. фон Рор (см. М. фон Рор, Die Bilderzeugung in optischen Instrumenten, pp. 317–323) представили метод Кербера, вывели формулы Зейделя из геометрических соображений, основанных на методе Аббе, и интерпретировали аналитические результаты геометрически (стр. 212–316).^[6]

Аберрации также могут быть выражены с помощью характеристическая функция системы и ее дифференциальных коэффициентов вместо радиусов и т. д. линз; эти формулы не применимы непосредственно, но дают, однако, соотношение между числом аберраций и порядком. Сэр Уильям Роуэн Гамильтон (British Assoc. Report, 1833, стр. 360), таким образом, вывел аберрации третьего порядка; а в более поздние времена этот метод продолжил клерк Максвелл (Proc. Лондонская математика. Soc., 1874–1875; (см. также трактаты Р. С. Хита и Л. А. Германа), М. Тизена (Берлин. Акад. Sitzber., 1890, 35, с. 804), Х. Брунс (Лейпциг. Математика. Phys. Бер., 1895, 21, с. 410), и особенно удачно К. Шварцшильд (Гёттинген. Акад. Abhandl., 1905, 4, No. 1), который таким образом открыл аберрации 5-го порядка (их девять) и, возможно, кратчайшее доказательство практических (Зейделя) формул. А. Гуллстранд (см. Выше, и Анна. d. Phys., 1905, 18, с. 941) основал свою теорию аберраций на дифференциальной геометрии поверхностей.^[6]

Аберрации третьего порядка: (1) аберрация точки оси; 2) аберрация точек, расстояние от оси которых очень мало, меньше третьего порядка - отклонение от синусоидального состояния и кома здесь попадают вместе в один класс; (3) астигматизм; (4) кривизна поля; (5) искажение.^[6]

(1) Аберрация третьего порядка точек оси рассматривается во всех учебниках по оптике. Это очень важно в конструкции телескопа. В телескопах апертура обычно принимается за линейный диаметр объектива. Это не то же самое, что апертура микроскопа, которая основана на входном зрачке или поле зрения, если смотреть со стороны объекта, и выражается как угловое измерение. Аберрациями высших порядков в конструкции телескопа можно по большей части пренебречь. Для микроскопов этим нельзя пренебрегать. Для одиночной линзы очень малой толщины и заданной оптической силы аберрация зависит от отношения радиусов r: r 'и является минимумом (но никогда не равна нулю) для определенного значения этого отношения; он изменяется обратно пропорционально показателю преломления (сила линзы остается постоянной). Общая аберрация двух или более очень тонких линз в контакте, являющаяся суммой индивидуальных аберраций, может быть равна нулю. Это также возможно, если линзы имеют одинаковый алгебраический знак. Из тонких положительных линз с n = 1,5 четыре необходимы для коррекции сферической аберрации третьего порядка. Однако эти системы не имеют большого практического значения. В большинстве случаев комбинируются две тонкие линзы, одна из которых имеет очень сильную положительную аберрацию (недокоррекция, см. выше) в качестве другого отрицательного; первая должна быть положительной линзой, а вторая - отрицательной линзой; однако сила света может отличаться, так что желаемый эффект линзы сохраняется. Как правило, преимуществом является обеспечение большого эффекта преломления несколькими линзами более слабыми, чем одной линзой с большим увеличением. С помощью одной, а также нескольких и даже бесконечного числа соприкасающихся тонких линз можно воспроизвести не более двух точек оси без аберрации третьего порядка. Свобода от аберрации для двух точек оси, одна из которых бесконечно удалена, известна как Состояние Гершеля. Все эти правила действительны, поскольку толщина и расстояние линз не должны приниматься во внимание.^[6]

(2) Условие выхода из комы третьего порядка также важно для объективов телескопов; это известно как Фраунгофера условие. (4) После устранения аберрации на оси, комы и астигматизма соотношение плоскостности поля в третьем порядке выражается соотношением Уравнение Пецваля, S1 / r (n'-n) = 0, где r - радиус преломляющей поверхности, n и n '- показатели преломления соседних сред, а S - знак суммы для всех преломляющих поверхностей.^[6]

Практическое устранение аберраций

Лазерные направляющие звезды помогают в устранении атмосферных искажений.^[15]

Классическая задача визуализации состоит в том, чтобы точно воспроизвести конечную плоскость (объект) на другой плоскости (изображение) через конечную апертуру. Невозможно сделать это идеально для больше одного такая пара плоскостей (это было доказано со все большей общностью Максвелл в 1858 г., Брунсом в 1895 г. и Каратеодори в 1926 г., см. резюме в Walther, A., J. Opt. Soc. Являюсь. А 6Т. 415–422 (1989)). Однако для одной пары плоскостей (например, для одной настройки фокуса объектива) проблема в принципе может быть решена идеально. Примеры такой теоретически совершенной системы включают: Люнебургская линза и Максвелл рыбий глаз.

Практические методы решают эту проблему с точностью, которая в большинстве случаев достаточна для специального назначения каждого вида инструментов. Проблема поиска системы, которая воспроизводит данный объект на данной плоскости с заданным увеличением (в той мере, в какой должны быть приняты во внимание аберрации), может быть решена с помощью теории приближения; в большинстве случаев, однако, аналитические трудности были слишком велики для старых методов расчета, но их можно облегчить путем применения современных компьютерных систем. Однако решения были получены в частных случаях (см. A. Konig в M. von Rohr's Die Bilderzeugung, п. 373; К. Шварцшильд, Геттинген. Акад. Abhandl., 1905, 4, №№ 2 и 3). В настоящее время конструкторы почти всегда используют обратный метод: они составляют систему из определенного, часто довольно личного опыта, и проверяют, путем тригонометрического расчета траекторий нескольких лучей, дает ли система желаемое воспроизведение (примеры приведены в А. Глейхен, Lehrbuch der geometrischen Optik, Лейпциг и Берлин, 1902 г.). Радиусы, толщины и расстояния постоянно изменяются до тех пор, пока ошибки изображения не станут достаточно малыми. Этим методом исследуются только определенные ошибки воспроизведения, особенно отдельные члены или все из перечисленных выше. The analytical approximation theory is often employed provisionally, since its accuracy does not generally suffice.^[6]

In order to render spherical aberration and the deviation from the sine condition small throughout the whole aperture, there is given to a ray with a finite angle of aperture u* (width infinitely distant objects: with a finite height of incidence h*) the same distance of intersection, and the same sine ratio as to one neighboring the axis (u* or h* may not be much smaller than the largest aperture U or H to be used in the system). The rays with an angle of aperture smaller than u* would not have the same distance of intersection and the same sine ratio; these deviations are called зоны, and the constructor endeavors to reduce these to a minimum. The same holds for the errors depending upon the angle of the field of view, w: astigmatism, curvature of field and distortion are eliminated for a definite value, w*, zones of astigmatism, curvature of field and distortion, attend smaller values of w. The practical optician names such systems: corrected for the angle of aperture u* (the height of incidence h*) or the angle of field of view w*. Spherical aberration and changes of the sine ratios are often represented graphically as functions of the aperture, in the same way as the deviations of two astigmatic image surfaces of the image plane of the axis point are represented as functions of the angles of the field of view.^[6]

The final form of a practical system consequently rests on compromise; enlargement of the aperture results in a diminution of the available field of view, and vice versa. But the larger aperture will give the larger resolution. The following may be regarded as typical:^[6]

(1) Largest aperture; necessary corrections are — for the axis point, and sine condition; errors of the field of view are almost disregarded; example — high-power microscope objectives.

(2) Wide angle lens; necessary corrections are — for astigmatism, curvature of field and distortion; errors of the aperture only slightly regarded; examples — photographic widest angle objectives and oculars.

Between these extreme examples stands the нормальный объектив: this is corrected more with regard to aperture; objectives for groups more with regard to the field of view.

(3) Long focus lenses have small fields of view and aberrations on axis are very important. Therefore zones will be kept as small as possible and design should emphasize simplicity. Because of this these lenses are the best for analytical computation.

Chromatic or color aberration

In optical systems composed of lenses, the position, magnitude and errors of the image depend upon the refractive indices of the glass employed (see Объектив (оптика) и Monochromatic aberration, над). Since the index of refraction varies with the color or wavelength of the light (see разброс ), it follows that a system of lenses (uncorrected) projects images of different colors in somewhat different places and sizes and with different aberrations; i.e. there are chromatic differences of the distances of intersection, of magnifications, and of monochromatic aberrations. If mixed light be employed (e.g. white light) all these images are formed and they cause a confusion, named chromatic aberration; for instance, instead of a white margin on a dark background, there is perceived a colored margin, or narrow spectrum. The absence of this error is termed achromatism, and an optical system so corrected is termed achromatic. A system is said to be chromatically under-corrected when it shows the same kind of chromatic error as a thin positive lens, otherwise it is said to be overcorrected.^[6]

If, in the first place, monochromatic aberrations be neglected — in other words, the Gaussian theory be accepted — then every reproduction is determined by the positions of the focal planes, and the magnitude of the focal lengths, or if the focal lengths, as ordinarily happens, be equal, by three constants of reproduction. These constants are determined by the data of the system (radii, thicknesses, distances, indices, etc., of the lenses); therefore their dependence on the refractive index, and consequently on the color,^[6] are calculable.^[16] The refractive indices for different wavelengths must be known for each kind of glass made use of. In this manner the conditions are maintained that any one constant of reproduction is equal for two different colors, i.e. this constant is achromatized. For example, it is possible, with one thick lens in air, to achromatize the position of a focal plane of the magnitude of the focal length. If all three constants of reproduction be achromatized, then the Gaussian image for all distances of objects is the same for the two colors, and the system is said to be in stable achromatism.^[6]

In practice it is more advantageous (after Abbe) to determine the chromatic aberration (for instance, that of the distance of intersection) for a fixed position of the object, and express it by a sum in which each component conlins the amount due to each refracting surface.^[17][18][6] In a plane containing the image point of one color, another colour produces a disk of confusion; this is similar to the confusion caused by two zones in spherical aberration. For infinitely distant objects the radius Of the chromatic disk of confusion is proportional to the linear aperture, and independent of the focal length (смотри выше, Monochromatic Aberration of the Axis Point); and since this disk becomes the less harmful with an increasing image of a given object, or with increasing focal length, it follows that the deterioration of the image is proportional to the ratio of the aperture to the focal length, i.e. the relative aperture. (This explains the gigantic focal lengths in vogue before the discovery of achromatism.)^[6]

Примеры:

(а) In a very thin lens, in air, only one constant of reproduction is to be observed, since the focal length and the distance of the focal point are equal. If the refractive index for one color be ${ displaystyle n}$, and for another ${displaystyle n+dn}$, and the powers, or reciprocals of the focal lengths, be ${ displaystyle f}$ и ${displaystyle f+df}$, then (1) ${displaystyle {dfrac {df}{f}}={dfrac {dn}{(n-1)}}={dfrac {1}{n}}}$; ${displaystyle dn}$ is called the dispersion, and ${ displaystyle n}$ the dispersive power of the glass.^[6]

(б) Two thin lenses in contact: let ${ displaystyle f_ {1}}$ и ${ displaystyle f_ {2}}$ be the powers corresponding to the lenses of refractive indices ${ displaystyle n_ {1}}$ и ${ displaystyle n_ {2}}$ and radii ${displaystyle r'_{1}}$, ${displaystyle r''_{1}}$, и ${displaystyle r'_{2}}$, ${displaystyle r''_{2}}$ соответственно; позволять ${ displaystyle f}$ denote the total power, and ${ displaystyle df}$, ${displaystyle dn_{1}}$, ${displaystyle dn_{2}}$ the changes of ${ displaystyle f}$, ${ displaystyle n_ {1}}$, и ${ displaystyle n_ {2}}$ with the color. Then the following relations hold:^[6]

(2) ${displaystyle f=f_{1}-f_{2}=(n_{1}-1)(1/r'_{1}-1/r''_{1})+(n2-1)(1/r'_{2}-1/r''_{2})=(n_{1}-1)k_{1}+(n_{2}-1)k_{2}}$; и

(3) ${displaystyle df=k_{1}dn_{1}+k_{2}dn_{2}}$. For achromatism ${displaystyle df=0}$, hence, from (3),

(4) ${displaystyle k_{1}/k_{2}=-dn_{2}/dn_{1}}$, или же ${displaystyle f_{1}/f_{2}=-n_{1}/n_{2}}$. Следовательно ${ displaystyle f_ {1}}$ и ${ displaystyle f_ {2}}$ must have different algebraic signs, or the system must be composed of a collective and a dispersive lens. Consequently the powers of the two must be different (in order that ${ displaystyle f}$ be not zero (equation 2)), and the dispersive powers must also be different (according to 4).

Newton failed to perceive the existence of media of different dispersive powers required by achromatism; consequently he constructed large reflectors instead of refractors. James Gregory and Leonhard Euler arrived at the correct view from a false conception of the achromatism of the eye; this was determined by Chester More Hall in 1728, Klingenstierna in 1754 and by Dollond in 1757, who constructed the celebrated achromatic telescopes. (Видеть telescope.)^[6]

Glass with weaker dispersive power (greater ${ displaystyle v}$) назван crown glass; that with greater dispersive power, бесцветное стекло. For the construction of an achromatic collective lens (${ displaystyle f}$ positive) it follows, by means of equation (4), that a collective lens I. of crown glass and a dispersive lens II. of flint glass must be chosen; the latter, although the weaker, corrects the other chromatically by its greater dispersive power. For an achromatic dispersive lens the converse must be adopted. This is, at the present day, the ordinary type, e.g., of telescope objective; the values of the four radii must satisfy the equations (2) and (4). Two other conditions may also be postulated: one is always the elimination of the aberration on the axis; the second either the Herschel или же Fraunhofer Condition, the latter being the best vide supra, Monochromatic Aberration). In practice, however, it is often more useful to avoid the second condition by making the lenses have contact, i.e. equal radii. According to P. Rudolph (Eder's Jahrb. f. Photog., 1891, 5, p. 225; 1893, 7, p. 221), cemented objectives of thin lenses permit the elimination of spherical aberration on the axis, if, as above, the collective lens has a smaller refractive index; on the other hand, they permit the elimination of astigmatism and curvature of the field, if the collective lens has a greater refractive index (this follows from the Petzval equation; see L. Seidel, Astr. Nachr., 1856, p. 289). Should the cemented system be positive, then the more powerful lens must be positive; and, according to (4), to the greater power belongs the weaker dispersive power (greater ${ displaystyle v}$), that is to say, crown glass; consequently the crown glass must have the greater refractive index for astigmatic and plane images. In all earlier kinds of glass, however, the dispersive power increased with the refractive index; то есть, ${ displaystyle v}$ decreased as ${ displaystyle n}$ increased; but some of the Jena glasses by E. Abbe and O. Schott were crown glasses of high refractive index, and achromatic systems from such crown glasses, with flint glasses of lower refractive index, are called the new achromats, and were employed by P. Rudolph in the first anastigmats (photographic objectives).^[6]

Instead of making ${ displaystyle df}$ vanish, a certain value can be assigned to it which will produce, by the addition of the two lenses, any desired chromatic deviation, e.g. sufficient to eliminate one present in other parts of the system. If the lenses I. and II. be cemented and have the same refractive index for one color, then its effect for that one color is that of a lens of one piece; by such decomposition of a lens it can be made chromatic or achromatic at will, without altering its spherical effect. If its chromatic effect (${displaystyle df/f}$) be greater than that of the same lens, this being made of the more dispersive of the two glasses employed, it is termed hyper-chromatic.^[6]

For two thin lenses separated by a distance ${ displaystyle D}$ the condition for achromatism is ${displaystyle D=v_{1}f_{1}+v_{2}f_{2}}$; если ${displaystyle v_{1}=v_{2}}$ (e.g. if the lenses be made of the same glass), this reduces to ${displaystyle D=(f_{1}+f_{2})/2}$, известный как condition for oculars.^[6]

If a constant of reproduction, for instance the focal length, be made equal for two colors, then it is not the same for other colors, if two different glasses are employed. For example, the condition for achromatism (4) for two thin lenses in contact is fulfilled in only one part of the spectrum, since ${displaystyle dn_{2}/dn_{1}}$ varies within the spectrum. This fact was first ascertained by J. Fraunhofer, who defined the colors by means of the dark lines in the solar spectrum; and showed that the ratio of the dispersion of two glasses varied about 20% from the red to the violet (the variation for glass and water is about 50%). If, therefore, for two colors, a and b, ${displaystyle f_{a}=f_{b}=f}$, then for a third color, c, the focal length is different; that is, if c lies between a and b, then ${displaystyle f_{c}$, and vice versa; these algebraic results follow from the fact that towards the red the dispersion of the positive crown glass preponderates, towards the violet that of the negative flint. These chromatic errors of systems, which are achromatic for two colors, are called the secondary spectrum, and depend upon the aperture and focal length in the same manner as the primary chromatic errors do.^[6]

In fig. 6, taken from M. von Rohr's Theorie und Geschichte des photographischen Objectivs, the abscissae are focal lengths, and the ordinates wavelengths. В Линии фраунгофера used are shown in adjacent table.^[6]

Figure 6

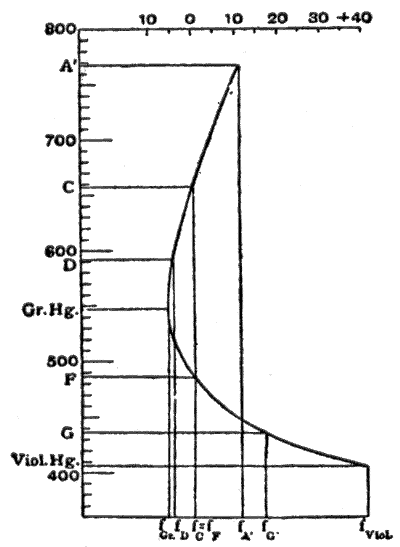
The focal lengths are made equal for the lines C and F. In the neighborhood of 550 nm the tangent to the curve is parallel to the axis of wavelengths; and the focal length varies least over a fairly large range of color, therefore in this neighborhood the color union is at its best. Moreover, this region of the spectrum is that which appears brightest to the human eye, and consequently this curve of the secondary on spectrum, obtained by making ${displaystyle f_{C}=f_{F}}$, is, according to the experiments of Sir G. G. Stokes (Proc. Roy. Soc., 1878), the most suitable for visual instruments (optical achromatism,). In a similar manner, for systems used in photography, the vertex of the color curve must be placed in the position of the maximum sensibility of the plates; this is generally supposed to be at G'; and to accomplish this the F and violet mercury lines are united. This artifice is specially adopted in objectives for astronomical photography (pure actinic achromatism). For ordinary photography, however, there is this disadvantage: the image on the focusing-screen and the correct adjustment of the photographic sensitive plate are not in register; in astronomical photography this difference is constant, but in other kinds it depends on the distance of the objects. On this account the lines D and G' are united for ordinary photographic objectives; the optical as well as the actinic image is chromatically inferior, but both lie in the same place; and consequently the best correction lies in F (this is known as the actinic correction или же freedom from chemical focus).^[6]

Should there be in two lenses in contact the same focal lengths for three colours a, b, and c, i.e. ${displaystyle f_{a}=f_{b}=f_{c}=f}$, then the relative partial dispersion ${displaystyle (n_{c}-n_{b})(n_{a}-n_{b})}$ must be equal for the two kinds of glass employed. This follows by considering equation (4) for the two pairs of colors ac and bc. Until recently no glasses were known with a proportional degree of absorption; but R. Blair (Trans. Edin. Soc., 1791, 3, p. 3), P. Barlow, and F. S. Archer overcame the difficulty by constructing fluid lenses between glass walls. Fraunhofer prepared glasses which reduced the secondary spectrum; but permanent success was only assured on the introduction of the Jena glasses by E. Abbe and O. Schott. In using glasses not having proportional dispersion, the deviation of a third colour can be eliminated by two lenses, if an interval be allowed between them; or by three lenses in contact, which may not all consist of the old glasses. In uniting three colors an achromatism of a higher order is derived; there is yet a residual tertiary spectrum, but it can always be neglected.^[6]

The Gaussian theory is only an approximation; monochromatic or spherical aberrations still occur, which will be different for different colors; and should they be compensated for one color, the image of another color would prove disturbing. The most important is the chromatic difference of aberration of the axis point, which is still present to disturb the image, after par-axial rays of different colors are united by an appropriate combination of glasses. If a collective system be corrected for the axis point for a definite wavelength, then, on account of the greater dispersion in the negative components — the flint glasses, — overcorrection will arise for the shorter wavelengths (this being the error of the negative components), and under-correction for the longer wavelengths (the error of crown glass lenses preponderating in the red). This error was treated by Jean le Rond d'Alembert, and, in special detail, by C. F. Gauss. It increases rapidly with the aperture, and is more important with medium apertures than the secondary spectrum of par-axial rays; consequently, spherical aberration must be eliminated for two colors, and if this be impossible, then it must be eliminated for those particular wavelengths which are most effectual for the instrument in question (a graphical representation of this error is given in M. von Rohr, Theorie und Geschichte des photographischen Objectivs).^[6]

The condition for the reproduction of a surface element in the place of a sharply reproduced point — the constant of the sine relationship must also be fulfilled with large apertures for several colors. E. Abbe succeeded in computing microscope objectives free from error of the axis point and satisfying the sine condition for several colors, which therefore, according to his definition, were aplanatic for several colors; such systems he termed apochromatic. While, however, the magnification of the individual zones is the same, it is not the same for red as for blue; and there is a chromatic difference of magnification. This is produced in the same amount, but in the opposite sense, by the oculars, which Abbe used with these objectives (compensating oculars), so that it is eliminated in the image of the whole microscope. The best telescope objectives, and photographic objectives intended for three-color work, are also apochromatic, even if they do not possess quite the same quality of correction as microscope objectives do. The chromatic differences of other errors of reproduction have seldom practical importances.^[6]

Смотрите также

• Аберрации глаза
• Optical telescope#The five Seidel aberrations
• Wavefront coding

Рекомендации

внешняя ссылка

• Microscope Objectives: Optical Aberrations раздел Molecular Expressions website, Michael W. Davidson, Mortimer Abramowitz, Olympus America Inc., and The Florida State University