Геометрическая оптика - Википедия - Geometrical optics
Геометрическая оптика, или же лучевая оптика, это модель оптика это описывает свет распространение с точки зрения лучи. Луч в геометрической оптике - это абстракция полезно для аппроксимации путей, по которым распространяется свет при определенных обстоятельствах.
Упрощающие предположения геометрической оптики включают в себя то, что световые лучи:
- распространяются по прямолинейным путям, когда они движутся в однородный средний
- изгибаться, и в определенных обстоятельствах может расколоться надвое, на интерфейс между двумя непохожими средства массовой информации
- следовать изогнутым путям в среде, в которой показатель преломления изменения
- могут быть поглощены или отражены.
Геометрическая оптика не учитывает некоторые оптические эффекты, такие как дифракция и вмешательство. Это упрощение полезно на практике; это отличное приближение, когда длина волны мала по сравнению с размером структур, с которыми взаимодействует свет. Эти методы особенно полезны при описании геометрических аспектов визуализация, включая оптические аберрации.
Объяснение

Луч света - это линия или же изгиб то есть перпендикуляр к свету волновые фронты (и поэтому коллинеарен с волновой вектор Несколько более строгое определение светового луча следует из Принцип Ферма, в котором говорится, что путь, пройденный лучом света между двумя точками, - это путь, который можно пройти за наименьшее время.[1]
Часто геометрическую оптику упрощают, делая параксиальное приближение, или «приближение малых углов». Тогда математическое поведение становится линейный, позволяя описывать оптические компоненты и системы простыми матрицами. Это приводит к методам Гауссова оптика и параксиальный трассировка лучей, которые используются для определения основных свойств оптических систем, таких как приблизительные изображение и позиции объекта и увеличения.[2]
Отражение

Глянцевые поверхности, такие как зеркала отражать свет простым и предсказуемым способом. Это позволяет создавать отраженные изображения, которые можно связать с фактическим (настоящий ) или экстраполированный (виртуальный ) расположение в космосе.
На таких поверхностях направление отраженного луча определяется углом, под которым падающий луч образует нормальная поверхность, линия, перпендикулярная поверхности в точке попадания луча. Падающий и отраженный лучи лежат в одной плоскости, а угол между отраженным лучом и нормалью к поверхности такой же, как и между падающим лучом и нормалью.[3] Это известно как Закон отражения.
За плоские зеркала, закон отражения подразумевает, что изображения объектов находятся в вертикальном положении и на том же расстоянии за зеркалом, что и объекты перед зеркалом. Размер изображения такой же, как и размер объекта. (The увеличение плоского зеркала равна единице.) Из закона также следует, что зеркальные изображения находятся инвертированная четность, что воспринимается как инверсия слева направо.
Зеркала с изогнутыми поверхностями можно смоделировать трассировка лучей и используя закон отражения в каждой точке поверхности. За зеркала с параболическими поверхностями, параллельные лучи, падающие на зеркало, производят отраженные лучи, которые сходятся на общем фокус. Другие изогнутые поверхности также могут фокусировать свет, но с аберрациями из-за расходящейся формы, вызывающей размытие фокуса в пространстве. В частности, сферические зеркала демонстрируют сферическая аберрация. Изогнутые зеркала могут формировать изображения с увеличением больше или меньше единицы, и изображение может быть вертикальным или перевернутым. Вертикальное изображение, образованное отражением в зеркале, всегда виртуально, в то время как перевернутое изображение реально и может проецироваться на экран.[3]
Преломление
Этот раздел должен включать краткое содержание другой статьи или быть резюмирован в ней. (Июнь 2009 г.) |

Преломление возникает, когда свет проходит через область пространства с изменяющимся показателем преломления. Простейший случай преломления возникает, когда существует граница раздела однородной среды с показателем преломления и другая среда с показателем преломления . В таких ситуациях Закон Снеллиуса описывает результирующее отклонение светового луча:
куда и - углы между нормалью (к границе раздела) и падающей и преломленной волнами соответственно. Это явление также связано с изменением скорости света, как видно из приведенного выше определения показателя преломления, которое подразумевает:
куда и - скорости волн в соответствующих средах.[3]
Различные следствия закона Снеллиуса включают тот факт, что для световых лучей, идущих от материала с высоким показателем преломления к материалу с низким показателем преломления, взаимодействие с границей раздела может привести к нулевому пропусканию. Это явление называется полное внутреннее отражение и позволяет волоконная оптика технологии. Когда световые сигналы проходят по оптоволоконному кабелю, они подвергаются полному внутреннему отражению, что позволяет практически не терять свет по длине кабеля. Также возможно изготовление поляризованные световые лучи с использованием комбинации отражения и преломления: когда преломленный луч и отраженный луч образуют прямой угол, отраженный луч обладает свойством «плоской поляризации». Угол падения, необходимый для такого сценария, известен как Угол Брюстера.[3]
Закон Снеллиуса может быть использован для предсказания отклонения световых лучей при их прохождении через «линейную среду», если известны показатели преломления и геометрия среды. Например, распространение света через призма приводит к тому, что луч света отклоняется в зависимости от формы и ориентации призмы. Кроме того, поскольку разные частоты света имеют немного разные показатели преломления в большинстве материалов, преломление можно использовать для получения разброс спектры которые выглядят как радуги. Известно, что открытие этого явления при прохождении света через призму приписывают Исаак Ньютон.[3]
Некоторые среды имеют показатель преломления, который постепенно меняется в зависимости от положения, и, таким образом, лучи света изгибаются через среду, а не движутся по прямым линиям. Этот эффект и является причиной миражи наблюдается в жаркие дни, когда изменяющийся показатель преломления воздуха заставляет световые лучи изгибаться, создавая видимость зеркальных отражений на расстоянии (как если бы на поверхности водоема). Материал с переменным показателем преломления называется материалом с градиентным показателем преломления (GRIN) и имеет множество полезных свойств, используемых в современных технологиях оптического сканирования, включая копировальные аппараты и сканеры. Явление изучается в области градиентная оптика.[4]

Устройство, которое производит сходящиеся или расходящиеся световые лучи из-за преломления, известно как линза. Тонкие линзы создают точки фокусировки с обеих сторон, которые можно смоделировать с помощью уравнение производителя линз.[5] В общем, существует два типа линз: выпуклые линзы, которые заставляют параллельные световые лучи сходиться, и вогнутые линзы, которые заставляют параллельные световые лучи расходиться. Подробный прогноз того, как эти линзы производят изображения, можно сделать с помощью трассировки лучей, аналогичной изогнутым зеркалам. Подобно изогнутым зеркалам, тонкие линзы подчиняются простому уравнению, которое определяет положение изображений при определенном фокусном расстоянии () и расстояние до объекта ():
куда - это расстояние, связанное с изображением, которое по соглашению считается отрицательным, если на той же стороне линзы, что и объект, и положительным, если на противоположной стороне линзы.[5] Фокусное расстояние f считается отрицательным для вогнутых линз.
Входящие параллельные лучи фокусируются выпуклой линзой в перевернутое реальное изображение на расстоянии одного фокусного расстояния от линзы, на дальней стороне линзы.

Лучи от объекта на конечном расстоянии фокусируются дальше от линзы, чем фокусное расстояние; чем ближе объект к объективу, тем дальше изображение от объектива. В вогнутых линзах входящие параллельные лучи расходятся после прохождения через линзу таким образом, что кажется, что они возникли на вертикальном виртуальном изображении на расстоянии одного фокусного расстояния от линзы, на той же стороне линзы, к которой приближаются параллельные лучи. .
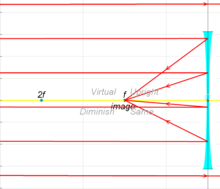
Лучи от объекта на конечном расстоянии связаны с виртуальным изображением, которое находится ближе к линзе, чем фокусное расстояние, и на той же стороне линзы, что и объект. Чем ближе объект к объективу, тем ближе виртуальное изображение к объективу.

Точно так же увеличение линзы определяется как
где отрицательный знак по соглашению используется для обозначения вертикального объекта для положительных значений и перевернутого объекта для отрицательных значений. Подобно зеркалам, вертикальные изображения, создаваемые одиночными линзами, виртуальны, а перевернутые изображения реальны.[3]
Линзы страдают от аберрации искажающие изображения и фокусные точки. Это связано как с геометрическими дефектами, так и с изменением показателя преломления для разных длин волн света (Хроматическая аберрация ).[3]
Основная математика
Как математическое исследование геометрическая оптика выступает как краткое изложение.длина волны предел для решений гиперболические уравнения в частных производных (Метод Зоммерфельда – Рунге) или как свойство распространения разрывов поля по уравнениям Максвелла (метод Люнебурга). В этом коротковолновом пределе решение можно аппроксимировать локально следующим образом:
куда удовлетворить соотношение дисперсии, а амплитуда меняется медленно. Точнее, ведущий заказ решение принимает форму
Фаза может быть линеаризован для восстановления большого волнового числа , а частота . Амплитуда удовлетворяет уравнение переноса. Малый параметр попадает на сцену из-за сильно колеблющихся начальных условий. Таким образом, когда начальные условия колеблются намного быстрее, чем коэффициенты дифференциального уравнения, решения будут сильно колебаться и переноситься вдоль лучей. Если предположить, что коэффициенты в дифференциальном уравнении гладкие, лучи тоже будут. Другими словами, преломление не происходит. Мотивация для этого метода исходит из изучения типичного сценария распространения света, когда свет с короткой длиной волны распространяется вдоль лучей, что минимизирует (более или менее) время его прохождения. Для его полного применения требуются инструменты от микролокальный анализ.
Метод Зоммерфельда – Рунге
Метод получения уравнений геометрической оптики с ограничением нулевой длины волны впервые описал Арнольд Зоммерфельд и Дж. Рунге в 1911 г.[6] Их вывод был основан на устном замечании Питер Дебай.[7][8] Рассмотрим монохроматическое скалярное поле , куда может быть любым из компонентов электрический или же магнитное поле а значит, функция удовлетворяют волновому уравнению
куда с будучи скорость света в вакууме. Здесь, это показатель преломления среды. Без ограничения общности введем преобразовать уравнение в
Поскольку основной принцип геометрической оптики лежит в пределе , предполагается следующий асимптотический ряд:
При большом, но конечном значении , ряд расходится, и нужно соблюдать осторожность, чтобы сохранить только подходящие первые несколько членов. Для каждого значения , можно найти оптимальное количество терминов, которые нужно сохранить, и добавление большего количества членов, чем оптимальное количество, может привести к худшему приближению.[9] Подставляя ряд в уравнение и собирая члены разного порядка, находим
в целом,
Первое уравнение известно как уравнение эйконала, что определяет эйконал это Уравнение Гамильтона – Якоби, записанный, например, в декартовых координатах, становится
Остальные уравнения определяют функции .
Люнебургский метод
Метод получения уравнений геометрической оптики на основе анализа поверхностей разрывов решений уравнений Максвелла впервые описал Рудольф Карл Люнебург в 1944 г.[10] Он не ограничивает электромагнитное поле специальной формой (в методе Зоммерфельда-Рунге не ясно, что поле, амплитуда которого сделан в зависимости от все равно приведет к уравнению эйконала, т. е. к волновому фронту геометрической оптики). Главный вывод такого подхода заключается в следующем:
Теорема. Предположим, что поля и (в линейной изотропной среде, описываемой диэлектрическими проницаемостями и ) имеют конечные разрывы вдоль поверхности, описываемой уравнением . Тогда из уравнений Максвелла в интегральной форме следует, что удовлетворяет уравнению эйконала:
- ,
куда - показатель преломления среды (гауссовы единицы).
Примером такой поверхности разрыва является начальный волновой фронт, исходящий от источника, который начинает излучать в определенный момент времени.
Таким образом, поверхности разрыва поля становятся волновыми фронтами геометрической оптики с соответствующими полями геометрической оптики, определяемыми как:
Эти поля подчиняются уравнениям переноса, согласующимся с уравнениями переноса подхода Зоммерфельда-Рунге. Световые лучи в теории Люнебурга определяются как траектории, ортогональные поверхностям разрыва, и при правильной параметризации можно показать, что они подчиняются принципу наименьшего времени Ферма, тем самым устанавливая тождество этих лучей со световыми лучами стандартной оптики.
Сказанное выше можно обобщить на анизотропные среды.[11]
Доказательство теоремы Люнебурга основано на исследовании того, как уравнения Максвелла управляют распространением разрывов решений. Основная техническая лемма выглядит следующим образом.
Техническая лемма. Позволять - гиперповерхность (трехмерное многообразие) в пространстве-времени на котором один или несколько из: , , , , имеют конечный разрыв. Тогда в каждой точке гиперповерхности верны формулы:
где оператор действует в -пространство (для каждого фиксированного ), а квадратные скобки обозначают разность значений по обе стороны от поверхности разрыва (настроены в соответствии с произвольным, но фиксированным соглашением, например, градиент указывая в направлении вычитаемых величин из).
Схема доказательства. Начнем с уравнений Максвелла вдали от источников (гауссовы единицы):
Используя теорему Стокса в из первого из приведенных выше уравнений можно сделать вывод, что для любой области в с кусочно гладкой границей верно следующее:
куда проекция наружной единичной нормали из на 3D-срез , и это объемная 3-форма на . Аналогичным образом из оставшихся уравнений Максвелла устанавливается следующее:
Теперь, рассматривая произвольные малые подповерхности из и создание небольших кварталов, окружающих в , и соответственно вычитая указанные выше интегралы, получаем:
куда обозначает градиент в 4D -Космос. И с тех пор произвольно, подынтегральные выражения должны быть равны 0, что доказывает лемму.
Теперь легко показать, что при распространении в сплошной среде поверхности разрыва подчиняются уравнению эйконала. В частности, если и непрерывны, то разрывы и удовлетворить: и . В этом случае первые два уравнения леммы можно записать в виде:
Взяв кросс-произведение первого уравнения с и подставив второй выход:
По второму из уравнений Максвелла , следовательно, для точек, лежащих на поверхности Только:
(Обратите внимание, что наличие разрыва важно на этом этапе, иначе мы бы делили на ноль.)
Исходя из физических соображений, без ограничения общности можно предположить, что имеет следующий вид:, т.е. двумерная поверхность, движущаяся в пространстве, смоделированная как ровные поверхности . (Математически существует если посредством теорема о неявной функции.) Вышеупомянутое уравнение, записанное в терминах становится:
т.е.
которое является уравнением эйконала и выполняется для всех , , , поскольку переменная отсутствует. Другие законы оптики, такие как Закон Снеллиуса и Формулы Френеля аналогично можно получить, рассматривая разрывы в и .
Общее уравнение с использованием четырехвекторной записи
В четырехвекторный обозначения, используемые в специальная теория относительности, волновое уравнение можно записать в виде
и замена приводит к[12]
Следовательно, уравнение эйконала имеет вид
Как только эйконал найден путем решения приведенного выше уравнения, волновой четырехвектор можно найти из
Смотрите также
Рекомендации
- ^ Артур Шустер, Введение в теорию оптики, Лондон: Эдвард Арнольд, 1904 г. онлайн.
- ^ Грейвенкамп, Джон Э. (2004). Полевое руководство по геометрической оптике. Полевые гиды SPIE. 1. SPIE. С. 19–20. ISBN 0-8194-5294-7.
- ^ а б c d е ж грамм Хью Д. Янг (1992). Университетская физика 8e. Эддисон-Уэсли. ISBN 0-201-52981-5. Глава 35.
- ^ Э. В. Марчанд, Gradient Index Optics, Нью-Йорк, Нью-Йорк, Academic Press, 1978.
- ^ а б Хехт, Юджин (1987). Оптика (2-е изд.). Эддисон Уэсли. ISBN 0-201-11609-X. Главы 5 и 6.
- ^ Зоммерфельд А. и Рунге Дж. (1911). Anwendung der Vektorrechnung auf die Grundlagen der geometrischen Optik. Annalen der Physik, 340 (7), 277-298.
- ^ Борн М. и Вольф Э. (2013). Основы оптики: электромагнитная теория распространения, интерференции и дифракции света.. Эльзевир.
- ^ http://www.neo-classical-physics.info/uploads/3/0/6/5/3065888/sommerfeld_-_geometrical_optics.pdf
- ^ Боровиц, С. (1967). Основы квантовой механики, частиц, волн и волновой механики.
- ^ Люнебург, Р. К., Математическая теория оптики, Brown University Press 1944 [заметки на мимеографе], University of California Press 1964
- ^ Клайн М., Кей И. В., Электромагнитная теория и геометрическая оптика, Interscience Publishers, 1965 г.
- ^ Ландау, Л. Д., и Лифшиц, Э. М. (1975). Классическая теория полей.
дальнейшее чтение
- Роберт Альфред Херман (1900) Трактат по геометрической оптике из Archive.org.
- «Свет глаз и просветленный пейзаж видения» рукопись на арабском языке о геометрической оптике, датируемая 16 веком.
- Теория систем лучей - В.Р. Гамильтон в Труды Ирландской королевской академии, Vol. XV, 1828 г.
Английские переводы некоторых ранних книг и статей
- Х. Брунс, "Дас Эйконал"
- М. Малус, "Оптика"
- Дж. Плюккер, "Обсуждение общего вида световых волн"
- Э. Куммер, "Общая теория прямолинейных лучевых систем"
- Э. Куммер, презентация оптически реализуемых прямолинейных лучевых систем
- Р. Мейбауэр, "Теория прямолинейных систем световых лучей"
- М. Паш, "О фокальных поверхностях лучевых систем и поверхностях особенностей комплексов"
- А. Левисталь, "Исследования в геометрической оптике"
- Ф. Кляйн, «О Брунском эйконале»
- Р. Донто, "Об интегральных инвариантах и некоторых моментах геометрической оптики"
- Т. де Дондер, "Об интегральных инвариантах оптики"































![{ displaystyle -k_ {o} ^ {2} A [( nabla S) ^ {2} -n ^ {2}] + 2ik_ {o} ( nabla S cdot nabla A) + ik_ {o} A nabla ^ {2} S + nabla ^ {2} A = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8b472952e8003d9916152f34e2369eee0f63a95)




















![{ displaystyle nabla varphi times [ mathbf { vec {H}}] - {1 over c} , varphi _ {t} , [ varepsilon mathbf { vec {E}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51b3c30c547b7c226171e4110cddbd75713808d6)
![{ displaystyle nabla varphi times [ mathbf { vec {E}}] + {1 over c} , varphi _ {t} , [ mu mathbf { vec {H}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ff1e61e92fa4da97a3d32989d1cff4c3bfb7c9d)
![{ Displaystyle набла cdot [ varepsilon mathbf { vec {E}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cf3428cb2edefd8ffe5f2c24f5fd5283ab876e2)
![{ Displaystyle набла cdot [ му mathbf { vec {H}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e71375bb0d578d28bea027a11613935fa158a61)



















![{ displaystyle oint _ { Gamma _ {0}} ( nabla varphi cdot [ varepsilon mathbf { vec {E}}]) , {dS over | nabla ^ {4D} varphi |} = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/765fd0c151f60c43f357280e247d260dc0581ee6)
![{ displaystyle oint _ { Gamma _ {0}} ( nabla varphi cdot [ mu mathbf { vec {H}}]) , {dS over | nabla ^ {4D} varphi |} = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13ce0be2f64e43744b3df2b6db3883789c3a4846)
![{ displaystyle oint _ { Gamma _ {0}} left ( nabla varphi times [ mathbf { vec {H}}] - {1 over c} , varphi _ {t} , [ varepsilon mathbf { vec {E}}] right) , {dS over | nabla ^ {4D} varphi |} = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2eb59d1d5e10d36ff203ba5b527aa04c658f50c)
![{ displaystyle oint _ { Gamma _ {0}} left ( nabla varphi times [ mathbf { vec {E}}] + {1 over c} , varphi _ {t} , [ mu mathbf { vec {H}}] right) , {dS over | nabla ^ {4D} varphi |} = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c1a586aa89bdb9bdc81fcf16a1a5502ae96f291)






![{ Displaystyle [ varepsilon mathbf { vec {E}}] = varepsilon [ mathbf { vec {E}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbf53b4b1af9d9e83460ea41a10b97adc5a17f1f)
![{ Displaystyle [ му mathbf { vec {H}}] = му [ mathbf { vec {H}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da51a3b1eae0a2d9c89358356d827fca38f5d178)
![{ displaystyle nabla varphi times [ mathbf { vec {H}}] - { varepsilon over c} , varphi _ {t} , [ mathbf { vec {E}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73dddb90e4cf5597724bc161094ddbe008d97d02)
![{ displaystyle nabla varphi times [ mathbf { vec {E}}] + { mu over c} , varphi _ {t} , [ mathbf { vec {H}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3789a6ee64532429305477a7a4ee4af8ce77655)
![{ displaystyle nabla varphi times ( nabla varphi times [ mathbf { vec {H}}]) - { varepsilon over c} , varphi _ {t} , ( nabla varphi times [ mathbf { vec {E}}]) = ( nabla varphi cdot [ mathbf { vec {H}}]) , nabla varphi - | nabla varphi | ^ {2} , [ mathbf { vec {H}}] + { varepsilon mu over c ^ {2}} varphi _ {t} ^ {2} , [ mathbf { vec { H}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c8f01b21e86dbdf41dc6b942f91827f8a42267)
![{ Displaystyle набла varphi cdot [ mathbf { vec {H}}] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef2ab28657425331a01e0e4879d0e96e2b689ab)














