Парадокс Фарадея - Faraday paradox

Майкл Фарадей

В Парадокс Фарадея или же Парадокс Фарадея это любой эксперимент, в котором Майкл Фарадей закон электромагнитная индукция похоже, предсказывает неверный результат. Парадоксы делятся на два класса:

• Закон Фарадея предсказывает, что не будет ЭДС но там ЭДС ненулевая.
• Похоже, что закон Фарадея предсказывает, что ЭДС будет отличной от нуля, но будет нулевая ЭДС.

Фарадей вывел свой закон индукции в 1831 году, после изобретения первого электромагнитного поля. генератор или же динамо, но никогда не удовлетворялся собственным объяснением парадокса.

Закон Фарадея в сравнении с уравнением Максвелла – Фарадея

Закон Фарадея (также известный как Закон Фарадея-Ленца) утверждает, что электродвижущая сила (ЭДС) определяется полная производная магнитного потока по времени т:

${ displaystyle { mathcal {E}} = - {d Phi _ {B} over dt}, }$

куда ${ displaystyle { mathcal {E}}}$ - ЭДС и Φ_B это магнитный поток. Направление электродвижущей силы определяется выражением Закон Ленца. Часто упускают из виду тот факт, что закон Фарадея основан на полной производной, а не на частной производной магнитного потока.^[1] Это означает, что ЭДС может возникать, даже если общий поток через поверхность постоянен. Чтобы решить эту проблему, можно использовать специальные методы. См. Ниже раздел о Использование специальных приемов с законом Фарадея. Однако наиболее распространенная интерпретация закона Фарадея такова:

Индуцированная электродвижущая сила в любой замкнутой цепи равна отрицательной величине скорости изменения во времени магнитный поток заключен в цепь.^[2][3]

Эта версия закона Фарадея строго соблюдается только тогда, когда замкнутый контур представляет собой петлю из бесконечно тонкой проволоки,^[4] и недействителен при других обстоятельствах. Он игнорирует тот факт, что закон Фарадея определяется полной, а не частной производной магнитного потока, а также тот факт, что ЭДС не обязательно ограничивается замкнутым контуром, но также может иметь радиальные компоненты, как обсуждается ниже. Другая версия, Уравнение Максвелла – Фарадея (обсуждается ниже), действует при любых обстоятельствах и при использовании в сочетании с законом силы Лоренца согласуется с правильным применением закона Фарадея.

Схема доказательства закона Фарадея из уравнений Максвелла и закона силы Лоренца.

Рассмотрим производную по времени потока через возможно движущийся контур с площадью ${ Displaystyle Sigma (т)}$: ${ displaystyle { frac {d Phi _ {B}} {dt}} = { frac {d} {dt}} int _ { Sigma (t)} mathbf {B} (t) cdot г mathbf {A}}$ Интеграл может изменяться со временем по двум причинам: подынтегральное выражение может измениться или область интегрирования может измениться. Следовательно, они складываются линейно: ${ displaystyle left. { frac {d Phi _ {B}} {dt}} right | _ {t = t_ {0}} = left ( int _ { Sigma (t_ {0}) } left. { frac { partial mathbf {B}} { partial t}} right | _ {t = t_ {0}} cdot d mathbf {A} right) + left ({ frac {d} {dt}} int _ { Sigma (t)} mathbf {B} (t_ {0}) cdot d mathbf {A} right)}$ куда т0 любое заданное фиксированное время. Покажем, что первое слагаемое в правой части соответствует ЭДС трансформатора, второе - ЭДС движения. Первый член в правой части можно переписать, используя интегральную форму уравнения Максвелла – Фарадея: ${ displaystyle int _ { Sigma (t_ {0})} left. { frac { partial mathbf {B}} { partial t}} right | _ {t = t_ {0}} cdot d mathbf {A} = - oint _ { partial Sigma (t_ {0})} mathbf {E} (t_ {0}) cdot d { boldsymbol { ell}}}$ Площадь, выметенная векторным элементом dℓ кривой ∂Σ во время dt при движении со скоростью v. Далее мы анализируем второй член в правой части: ${ displaystyle { frac {d} {dt}} int _ { Sigma (t)} mathbf {B} (t_ {0}) cdot d mathbf {A}}$ Это самая трудная часть доказательства; более подробную информацию и альтернативные подходы можно найти в справочных материалах.[5][6][7] По мере того как петля перемещается и / или деформируется, она выметает поверхность (см. Рисунок справа). Магнитный поток через эту вытянутую поверхность соответствует магнитному потоку, который либо входит, либо выходит из петли, и, следовательно, это магнитный поток, который вносит вклад в производную по времени. (Этот шаг неявно использует Закон Гаусса для магнетизма: Поскольку силовые линии не имеют ни начала, ни конца, они могут попасть в петлю, только будучи разрезанной проволокой.) Как небольшая часть петли. ${ displaystyle d { boldsymbol { ell}}}$ движется со скоростью v на короткое время ${ displaystyle dt}$, он выметает вектор векторной области ${ displaystyle d mathbf {A} = mathbf {v} , dt times d { boldsymbol { ell}}}$. Следовательно, изменение магнитного потока через петлю здесь равно ${ displaystyle mathbf {B} cdot ( mathbf {v} , dt times d { boldsymbol { ell}}) = - dt , d { boldsymbol { ell}} cdot ( mathbf {v} times mathbf {B})}$ Следовательно: ${ displaystyle { frac {d} {dt}} int _ { Sigma (t)} mathbf {B} (t_ {0}) cdot d mathbf {A} = - oint _ { partial Sigma (t_ {0})} ( mathbf {v} (t_ {0}) times mathbf {B} (t_ {0})) cdot d { boldsymbol { ell}}}$ куда v - скорость точки на петле ${ Displaystyle partial Sigma}$. Собирая их вместе, ${ displaystyle left. { frac {d Phi _ {B}} {dt}} right | _ {t = t_ {0}} = left (- oint _ { partial Sigma (t_ { 0})} mathbf {E} (t_ {0}) cdot d { boldsymbol { ell}} right) + left (- oint _ { partial Sigma (t_ {0})} ( mathbf {v} (t_ {0}) times mathbf {B} (t_ {0})) cdot d { boldsymbol { ell}} right)}$ Между тем, ЭДС определяется как энергия, доступная на единицу заряда, которая проходит один раз по проволочной петле. Поэтому по Закон силы Лоренца, ${ Displaystyle EMF = oint left ( mathbf {E} + mathbf {v} times mathbf {B} right) cdot { text {d}} { boldsymbol { ell}}}$ Объединяя их,${ displaystyle { frac {d Phi _ {B}} {dt}} = - ЭДС}$

Уравнение Максвелла-Фарадея является обобщением закона Фарадея, который гласит, что изменяющееся во времени магнитное поле всегда сопровождается изменяющимся в пространстве, неконсервативный электрическое поле, и наоборот. Уравнение Максвелла – Фарадея:

(в Единицы СИ ) куда ${ displaystyle partial}$ это частная производная оператор, ${ Displaystyle набла раз}$ это завиток оператор и опять E(р, т) это электрическое поле и B(р, т) это магнитное поле. Эти поля обычно могут быть функциями позиции р и время т.

Уравнение Максвелла – Фарадея - одно из четырех Уравнения Максвелла, и поэтому играет фундаментальную роль в теории классический электромагнетизм. Это также можно записать в интегральная форма посредством Теорема Кельвина – Стокса.^[8]

Парадоксы, в которых закон индукции Фарадея, кажется, предсказывает нулевую ЭДС, но на самом деле предсказывает ненулевую ЭДС

Эти парадоксы обычно разрешаются тем фактом, что ЭДС может создаваться изменением потока в цепи, как объяснено в законе Фарадея, или движением проводника в магнитном поле. Это объясняется Фейнманом, как указано ниже. См. Также А. Зоммерфельд, Том III. Электродинамика Academic Press, стр. 362.

Оборудование

Рисунок 1: Дисковый электрогенератор Фарадея. Диск вращается с угловой скоростью ω, перемещая проводящий диск по кругу в статическом магнитном поле. B за счет постоянного магнита. Магнитная сила Лоренца v × B направляет ток в радиальном направлении через проводящий диск к проводящему ободу, и оттуда контур цепи завершается через нижнюю щетку и ось, поддерживающую диск. Таким образом, ток возникает в результате механического движения.

Для эксперимента требуется несколько простых компонентов (см. Рисунок 1): цилиндрический магнит, проводящий диск с проводящим ободом, проводящая ось, некоторая проводка и гальванометр. Диск и магнит установлены на небольшом расстоянии друг от друга на оси, на которой они могут свободно вращаться вокруг своих осей симметрии. Электрическая цепь образуется подключением скользящих контактов: один к оси диска, другой к его ободу. В схему можно вставить гальванометр для измерения силы тока.

Процедура

Эксперимент проходит в три этапа:

1. Магнит удерживают, чтобы предотвратить его вращение, в то время как диск вращается вокруг своей оси. В результате гальванометр регистрирует постоянный ток. Таким образом, устройство действует как генератор, иначе называемый генератором Фарадея, Диск Фарадея, или униполярный (или униполярный) генератор.
2. Диск удерживается неподвижно, в то время как магнит вращается вокруг своей оси. В результате гальванометр не регистрирует ток.
3. Диск и магнит вращаются вместе. Гальванометр регистрирует ток, как это было на шаге 1.

Почему это парадоксально?

Эксперимент описывается некоторыми как «парадокс», поскольку на первый взгляд кажется, что он нарушает закон электромагнитной индукции Фарадея, поскольку поток через диск кажется одинаковым независимо от того, что вращается. Следовательно, прогнозируется, что ЭДС будет равна нулю во всех трех случаях вращения. Обсуждение ниже показывает, что эта точка зрения проистекает из неправильного выбора поверхности для расчета потока.

Парадокс выглядит несколько иначе с точки зрения потока: в модели электромагнитной индукции Фарадея магнитное поле состоял из воображаемых линии из магнитный поток, похожие на линии, которые появляются, когда железные опилки посыпают бумагу и держат рядом с магнитом. Предполагается, что ЭДС пропорциональна скорости резки линий потока. Если представить себе, что силовые линии возникают в магните, то они будут стационарными в рамке магнита, и вращение диска относительно магнита, будь то вращение магнита или диска, должно вызвать ЭДС, но вращение они оба вместе не должны.

Объяснение Фарадея

В модели электромагнитной индукции Фарадея цепь получает индуцированный ток, когда она разрезает линии магнитного потока. Согласно этой модели, диск Фарадея должен был работать, когда вращался либо диск, либо магнит, но не оба вместе. Фарадей попытался объяснить несогласие с наблюдениями, предположив, что поле магнита, вместе с его линиями потока, оставалось неподвижным при вращении магнита (полностью точная картина, но, возможно, не интуитивно понятная в модели линий потока). Другими словами, у линий потока есть своя собственная система отсчета. Как мы увидим в следующем разделе, современная физика (с момента открытия электрон ) не нуждается в потоковой картине и рассеивает парадокс.

Современные объяснения

Принимая во внимание обратный путь

В шаг 2, поскольку ток не наблюдается, можно сделать вывод, что магнитное поле не вращалось вместе с вращающимся магнитом. (Действует или не действует эффективно или относительно, сила Лоренца равна нулю, поскольку v равна нулю относительно лабораторной системы отсчета. Таким образом, измерения тока с помощью лабораторных рамок нет.) Использование уравнения Лоренца для объяснения этого парадокса привело к дискуссии в литературе относительно того, вращается ли магнитное поле вместе с магнитом. Поскольку сила, действующая на заряды, выраженная уравнением Лоренца, зависит от относительного движения магнитного поля (т. Е. Лабораторной рамы) к проводнику, где расположена ЭДС, предполагалось, что в случае, когда магнит вращается вместе с диском, но напряжение все еще развивается, магнитное поле (то есть лабораторная рамка) не должно поэтому вращаться вместе с магнитным материалом (конечно, поскольку это лабораторная рамка), в то время как эффективное определение рамки магнитного поля или «эффективное / относительное вращение поля» поворачивается без относительного движения относительно проводящего диска.

Тщательное размышление показало, что, если предположить, что магнитное поле вращается вместе с магнитом, а магнит вращается вместе с диском, ток все равно должен создаваться, а не за счет ЭДС в диске (нет относительного движения между диском и магнитом). но во внешней цепи, соединяющей щетки,^[9] который фактически движется относительно вращающегося магнита. (Кисти находятся в лабораторной раме.)

Этот механизм согласуется с наблюдениями, касающимися обратных путей: ЭДС генерируется всякий раз, когда диск движется относительно обратного пути, независимо от вращения магнита. Фактически было показано, что до тех пор, пока токовая петля используется для измерения наведенных ЭДС от движения диска и магнита, невозможно определить, вращается ли магнитное поле вместе с магнитом или нет. (Это зависит от определения, движение поля может быть определено только эффективно / относительно. Если вы придерживаетесь точки зрения, что поток поля является физическим объектом, он вращается или зависит от того, как он генерируется. Но это не меняет что используется в формуле Лоренца, особенно v, скорость носителя заряда относительно системы отсчета, в которой происходит измерение, и напряженность поля изменяется согласно теории относительности в любой точке пространства-времени.)

Было предложено несколько экспериментов с использованием электростатических измерений или электронных лучей для решения этой проблемы, но, по-видимому, ни один из них до сих пор не был успешно проведен.^{[нужна цитата ]}

Использование силы Лоренца

Сила Лоренца F на заряженная частица (заряда q) в движении (мгновенная скорость v). В E поле и B поле различаются в пространстве и времени.

Сила F действуя на частицу электрического заряда q с мгновенной скоростью v, за счет внешнего электрического поля E и магнитное поле B, задается силой Лоренца:^[10]

куда × - векторное векторное произведение. Все величины, выделенные жирным шрифтом, являются векторами. В релятивистски правильный электрическое поле точечного заряда изменяется со скоростью как:^[11]

${ displaystyle mathbf {E} = { frac {q} {4 pi epsilon _ {0}}} { frac {1-v ^ {2} / c ^ {2}} {(1-v ^ {2} sin ^ {2} theta / c ^ {2}) ^ {3/2}}} { frac { mathbf {{ hat {r}} '}} {| mathbf {r } '| ^ {2}}}}$

куда ${ displaystyle mathbf { hat {r}} '}$ - единичный вектор, указывающий от текущего (без запаздывания) положения частицы до точки, в которой измеряется поле, а θ - угол между ${ displaystyle mathbf {v}}$ и ${ displaystyle mathbf {r} '}$. Магнитное поле B заряда составляет:^[11]

${ displaystyle mathbf {B} = { frac {1} {c ^ {2}}} mathbf {v} times mathbf {E}}$

На самом нижнем уровне полная сила Лоренца - это совокупный результат электрических полей E и магнитные поля B каждого обвинения, действующего по любому другому обвинению.

Когда магнит вращается, но силовые линии неподвижны, а проводник неподвижен

Рассмотрим частный случай, когда цилиндрический проводящий диск неподвижен, а цилиндрический магнитный диск вращается. В такой ситуации средняя скорость v зарядов в проводящем диске изначально равна нулю, и поэтому магнитная сила F = qv × B равно 0, где v - средняя скорость заряда q схемы относительно кадра, на котором производятся измерения, и q - заряд электрона.

Когда магнит и магнитопроводы неподвижны, а проводник вращается

После открытия электрон и сил, влияющих на него, стало возможным микроскопическое разрешение парадокса. См. Рисунок 1. Металлические части устройства являются проводящими и ограничивают ток из-за электронного движения внутри металлических границ. Все электроны, движущиеся в магнитном поле, испытывают Сила Лоренца из F = qv × B, куда v - скорость электронов относительно системы отсчета, в которой производятся измерения, и q - заряд электрона. Помните, не существует такой рамки, как «рамка электромагнитного поля». Кадр устанавливается на конкретную точку пространства-времени, а не на расширяющееся поле или линию потока как математический объект. Другое дело, если рассматривать поток как физическую сущность (см. Квант магнитного потока ) или рассмотрите эффективное / относительное определение движения / вращения поля (см. ниже). Эта заметка помогает разрешить парадокс.

Сила Лоренца перпендикулярна как скорости электронов, которая находится в плоскости диска, так и нормальному магнитному полю (нормальная поверхность ) на диск. Электрон, находящийся в состоянии покоя в рамке диска, движется по кругу вместе с диском относительно B-поля (то есть оси вращения или лабораторной рамки, помните примечание выше), и поэтому испытывает радиальную силу Лоренца. На рисунке 1 эта сила (на положительный заряд, а не электрон) направлен наружу к ободу в соответствии с правилом правой руки.

Конечно, эта радиальная сила, которая является причиной тока, создает радиальную составляющую скорости электронов, генерируя, в свою очередь, свою собственную составляющую силы Лоренца, которая противодействует круговому движению электронов, стремясь замедлить вращение диска, но электроны сохраняют компонент кругового движения, который продолжает управлять током за счет радиальной силы Лоренца.

Использование специальных приемов с законом Фарадея

Поток через часть пути от щетки на ободе, через внешнюю петлю и ось к центру диска всегда равен нулю, потому что магнитное поле находится в плоскости этого пути (не перпендикулярно ему), нет независимо от того, что вращается, поэтому интегрированная ЭДС вокруг этой части пути всегда равна нулю. Поэтому внимание сосредоточено на участке пути от оси через диск до щетки на ободе.

Закон индукции Фарадея можно выразить словами:^[12]

Индуцированная электродвижущая сила или ЭДС в любой замкнутой цепи равна скорости изменения во времени магнитный поток через цепь.

Математически закон формулируется:

${ displaystyle { mathcal {E}} = - { frac {d Phi _ {B}} {dt}} = - { frac {d} {dt}} iint _ { Sigma (t)} d { boldsymbol {A}} cdot mathbf {B} ( mathbf {r}, t) ,}$

где Φ_B это поток, а dА - векторный элемент площади движущейся поверхности Σ(т), ограниченный петлей, вокруг которой должна быть найдена ЭДС.

Рисунок 2: Два возможных цикла для поиска ЭДС: геометрически простой путь прост в использовании, но другой обеспечивает такую ​​же ЭДС. Ни один из них не предназначен для имитации какой-либо линии физического тока.

Как этот закон может быть связан с генератором диска Фарадея, где магнитная связь представляет собой просто B-поле, умноженное на площадь диска?

Один из подходов состоит в том, чтобы определить понятие «скорость изменения потокосцепления», проведя гипотетическую линию поперек диска от щетки к оси и спросив, сколько потокосцеплений проходит мимо этой линии в единицу времени. См. Рисунок 2. Предполагая, что радиус р для диска - сектор диска с центральным углом θ имеет площадь:

${ displaystyle A = { frac { theta} {2 pi}} pi R ^ {2} ,}$

так что скорость прохождения потока мимо воображаемой линии равна

${ displaystyle { mathcal {E}} = - { frac {d Phi _ {B}} {dt}} = B { frac {dA} {dt}} = B { frac {R ^ { 2}} {2}} { frac {d theta} {dt}} = B { frac {R ^ {2}} {2}} omega ,}$

с ω = dθ / dt угловая скорость вращения. Знак выбирается исходя из Закон Ленца: поле, создаваемое движением, должно противодействовать изменению потока, вызванному вращением. Например, схема с радиальным сегментом на рисунке 2 по правилу правой руки добавляет к приложенному B-полю, стремясь увеличить потокосцепление. Это говорит о том, что поток через этот путь уменьшается из-за вращения, поэтому dθ / dt отрицательный.

Этот результат отсечения магнитного потока для ЭДС можно сравнить с расчетом работы, совершаемой на единицу заряда, заставляющую бесконечно малый пробный заряд пересечь гипотетическую линию, с использованием силы Лоренца на единицу заряда на радиусе р, а именно |v × B| = Bv = Brω:

${ displaystyle { mathcal {E}} = int _ {0} ^ {R} drBr omega = { frac {R ^ {2}} {2}} B omega ,}$

что и есть тот же результат.

Вышеупомянутая методология нахождения потока, отсекаемого цепью, формализована в законе потока путем правильной обработки производной по времени ограничивающей поверхности Σ (т). Конечно, производная по времени от интеграла с пределами, зависящими от времени, равна нет просто производная по времени от подынтегрального выражения, о чем часто забывают; видеть Интегральное правило Лейбница и Сила Лоренца.

При выборе поверхности Σ (т), ограничения заключаются в том, что (i) он должен быть ограничен замкнутой кривой, вокруг которой должна быть найдена ЭДС, и (ii) он должен фиксировать относительное движение всех движущихся частей цепи. Решительно нет Требуется, чтобы ограничивающая кривая соответствовала физической линии протекания тока. С другой стороны, индукция - это относительное движение, и путь решительно должен зафиксировать любое относительное движение. В случае, подобном Рисунку 1, где часть пути тока распределена по области в пространстве, ЭДС, управляющая током, может быть найдена с использованием множества путей. На рисунке 2 показаны две возможности. Все пути включают очевидную петлю возврата, но на диске показаны два пути: один - геометрически простой путь, другой - извилистый. Мы можем выбирать любой путь, который нам нравится, но часть любого приемлемого пути фиксируется в самом диске и крутится с диском. Поток рассчитывается по всему пути, обратный контур плюс сегмент диска, и найдена скорость его изменения.

Рисунок 3: Пример отображения диска Фарадея в скользящий проводящий прямоугольник. Диск рассматривается как кольцо; он разрезается по радиусу и сгибается, чтобы получился прямоугольник.

В этом примере все эти пути приводят к одинаковой скорости изменения магнитного потока и, следовательно, к одной и той же ЭДС. Чтобы дать некоторое представление об этой независимости пути, на рисунке 3 диск Фарадея развернут на полосу, что делает его похожим на задачу скользящего прямоугольника. В случае скользящего прямоугольника становится очевидным, что характер протекания тока внутри прямоугольника не зависит от времени и, следовательно, не имеет отношения к скорости изменения магнитного потока, соединяющего цепь. Нет необходимости точно учитывать, как ток проходит через прямоугольник (или диск). Любой выбор пути, соединяющего верх и низ прямоугольника (ось-щетку на диске) и перемещающийся с прямоугольником (вращающийся вместе с диском), обеспечивает одинаковую скорость изменения магнитного потока и предсказывает ту же ЭДС. . Для диска эта оценка скорости изменения магнитного потока такая же, как и оценка, сделанная выше, на основе вращения диска мимо линии, соединяющей щетку с осью.

Конфигурация с обратным путем

"Движется" ли магнит, не имеет значения в этом анализе из-за потока, индуцированного в обратном пути. Важнейшее относительное движение - это движение диска и обратного пути, а не диска и магнита. Это становится более ясным, если использовать модифицированный диск Фарадея, в котором обратным путем является не провод, а другой диск.То есть установите два токопроводящих диска рядом друг с другом на одной оси и дайте им скользящий электрический контакт в центре и по окружности. Ток будет пропорционален относительному вращению двух дисков и не зависит от вращения магнита.

Конфигурация без обратного пути

Диск Фарадея также может работать без гальванометра или обратного пути. Когда диск вращается, электроны собираются вдоль обода и оставляют дефицит около оси (или наоборот). В принципе можно измерить распределение заряда, например, через электродвижущая сила возникает между ободом и осью (хотя и не обязательно легко). Это разделение зарядов будет пропорционально относительной скорости вращения диска и магнита.

Парадоксы, в которых закон индукции Фарадея, кажется, предсказывает ненулевую ЭДС, но фактически предсказывает нулевую ЭДС

Эти парадоксы обычно разрешаются путем определения того, что кажущееся движение контура на самом деле представляет собой деконструкцию контура с последующей реконструкцией контура на другом пути.

Дополнительное правило

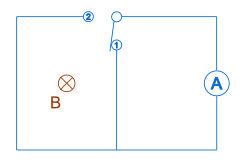
В том случае, когда вращается только диск, поток через контур не изменяется, однако возникает электродвижущая сила, индуцированная вопреки закону Фарадея. Мы также можем показать пример, когда есть изменение потока, но нет индуцированного напряжения. На рисунке 5 (справа) показана установка, использованная в эксперименте Тилли.^[13] Это схема с двумя петлями или сетками. Гальванометр подключен к правой петле, магнит в центре левой петли, переключатель в левой петле и переключатель между петлями. Начнем с того, что переключатель слева открыт, а переключатель справа - закрыт. Когда переключатель слева замкнут, а переключатель справа разомкнут, поле магнита не изменяется, но изменяется площадь цепи гальванометра. Это означает, что есть изменение потока. Однако гальванометр не отклонялся, что означает отсутствие наведенного напряжения, и закон Фарадея в этом случае не работает. Согласно А.Г. Келли, это предполагает, что индуцированное напряжение в эксперименте Фарадея возникает из-за «перерезания» цепи магнитными линиями, а не из-за «магнитной связи» или фактического изменения магнитного потока. Это следует из эксперимента Тилли, поскольку силовые линии в цепи не перемещаются и, следовательно, не индуцируется ток, хотя поток через цепь изменяется. Нуссбаум предполагает, что для того, чтобы закон Фарадея имел силу, необходимо проделать работу по изменению потока.^[14]
Чтобы понять эту идею, мы рассмотрим аргумент Нуссбаума.^[14] Начнем с расчета силы между двумя токоведущими проводами. Усилие на проводе 1, создаваемое проводом 2, определяется следующим образом:

${ displaystyle mathbf {F} _ {21} = { frac { mu _ {0}} {4 pi}} I_ {1} I_ {2} oint _ {C_ {1}} oint _ {C_ {2}} { frac {d mathbf {l_ {1}} mathbf { times} (d mathbf {l_ {2}} mathbf { times} { hat { mathbf {r}}} _ {21})} {r_ {21} ^ {2}}} }$

Магнитное поле от второго провода определяется выражением:

${ displaystyle mathbf {B} _ {2} = { frac { mu _ {0}} {4 pi}} I_ {2} oint _ {C_ {2}} { frac {(d mathbf {l_ {2}} mathbf { times} { hat { mathbf {r}}} _ {21})} {r_ {21} ^ {2}}} }$

Таким образом, мы можем переписать силу на проводе 1 как:

${ displaystyle mathbf {F} _ {21} = I_ {1} oint _ {C_ {1}} d mathbf {l_ {1}} mathbf { times} mathbf {B} _ {2 }}$

Теперь рассмотрим сегмент ${ displaystyle d mathbf {l}}$ смещенного проводника ${ displaystyle d mathbf {r}}$ в постоянном магнитном поле. Информация о проделанной работе:

${ displaystyle dW = d mathbf {F} cdot d mathbf {r}}$

Если мы подключим то, что мы ранее нашли для ${ displaystyle d mathbf {F}}$ мы получили:

${ displaystyle dW = (идентификатор mathbf {l} mathbf { times} mathbf {B}) cdot d mathbf {r}}$

Площадь, охватываемая смещением проводника:

${ displaystyle d mathbf {S} = d mathbf {r} mathbf { times} d mathbf {l}}$

Следовательно:

${ displaystyle dW = I mathbf {B} cdot d mathbf {S} = Id Phi _ {B}}$

Дифференциальная работа также может быть выражена в виде заряда. ${ displaystyle dq}$ и разность потенциалов ${ displaystyle V}$:

${ displaystyle dW = Vdq = VIdt}$

Уравнивая два уравнения для дифференциальной работы, мы приходим к закону Фарадея.

${ displaystyle d Phi _ {B} = Vdt}$

Более того, теперь мы видим, что это верно, только если ${ displaystyle dW}$ не исчезает. Это означает, что закон Фарадея действителен только в том случае, если выполняется работа по изменению потока.

Математический способ подтвердить закон Фарадея в подобных ситуациях - это обобщить определение ЭДС как в доказательстве Закон индукции Фарадея:

${ Displaystyle EMF = oint left ( mathbf {E} + mathbf {v} times mathbf {B} right) cdot { text {d}} { boldsymbol { ell}}}$

Гальванометр обычно измеряет только первый член в ЭДС, который вносит вклад в ток в цепи, хотя иногда он может измерять включение второго члена, например, когда второй член вносит вклад в часть тока, который гальванометр измеряет как ЭДС движения, например в эксперименте с диском Фарадея. В приведенной выше ситуации первый член равен нулю, и только первый член ведет ток, который измеряет гальванометр, поэтому наведенное напряжение отсутствует. Однако закон Фарадея по-прежнему остается в силе, поскольку очевидное изменение магнитного потока относится ко второму члену в приведенном выше обобщении ЭДС. Но гальванометром это не измеряется. Помните ${ displaystyle mathbf {v}}$ - это локальная скорость точки в цепи, а не носитель заряда. В конце концов, обе / все эти ситуации согласуются с заботой об относительности и микроструктуре материи и / или полнотой уравнения Максвелла и формулы Лоренца, или их комбинации, Гамильтонова механика.

Смотрите также

• Закон индукции Фарадея
• Сила Лоренца
• Проблема с подвижным магнитом и проводником
• Электрическое поле коротации

Рекомендации

дальнейшее чтение

• Майкл Фарадей, Экспериментальные исследования электричества, том I, первая серия, 1831 г. в Великих книгах западного мира, том 45, Р. М. Хатчинс, изд., Encyclopdia Britannica, Inc., Чикагский университет, 1952. [1]
• «Электромагнитная индукция: физика и воспоминания» (PDF) Джузеппе Джулиани - детали силы Лоренца в диске Фарадея
• «Униполярное электрическое динамо» - содержит вывод уравнения для ЭДС диска Фарадея
• Колонка Дона Ланкастера "Tech Musings", февраль 1998 г. - о практической неэффективности диска Фарадея
• "Последняя загадка Фарадея: вращается ли поле с помощью магнита?" (PDF) - противоположная теория, но содержит полезные ссылки на эксперименты Фарадея
• П. Дж. Скэнлон, Р. Н. Хенриксен и Дж. Р. Аллен, "Подходы к электромагнитной индукции", Am. J. Phys. 37, 698–708 (1969). - описывает, как применить закон Фарадея к диску Фарадея
• Хорхе Гуала-Вальверде, Педро Маццони, Рикардо Ахиллес «Униполярный двигатель: настоящий релятивистский двигатель», Am. J. Phys. 70 (10), 1052–1055 (октябрь 2002 г.). - утверждает, что только сила Лоренца может объяснить диск Фарадея, и описывает некоторые экспериментальные доказательства этого
• Фрэнк Манли, вызовы правилу потока Фарадея, Am. J. Phys. 72, 1478 (2004). - обновленное обсуждение концепций в ссылке Scanlon выше.
• Ричард Фейнман, Роберт Лейтон, Мэтью Сэндс, «Лекции Фейнмана по физике, том II», глава 17 - В дополнение к «парадоксу» Фарадея (где связанный поток не изменяется, но индуцируется ЭДС), он описывает «качающиеся пластины. «эксперимент, в котором связанный поток изменяется, но не индуцируется ЭДС. Он показывает, что правильную физику всегда дает комбинация Сила Лоренца с уравнением Максвелла – Фарадея (см. вставку для цитат) и ставит эти два собственных «парадокса».
• Вращение магнитного поля Автор: Ваня Янезич - описывает простой эксперимент, который может сделать каждый. Поскольку в нем участвуют только два тела, его результат менее неоднозначен, чем эксперименты Фарадея, Келли и Гуала-Вальверде с тремя телами.
• У. Ф. Хьюз и Ф. Дж. Янг, Электромагнитодинамика жидкостей, John Wiley & Sons (1965) LCCC # 66-17631. Главы 1. Основы специальной теории относительности и 2. Электродинамика движущихся сред. Из этих глав можно проработать все проблемы наведенной ЭДС и объяснить все связанные с ними парадоксы, обнаруженные в литературе.