Свободная булева алгебра - Free Boolean algebra

В математика, а свободная булева алгебра это Булева алгебра с выделенным набором элементов, называемых генераторы, такое, что:

Каждый элемент булевой алгебры может быть выражен как конечная комбинация генераторов с использованием булевых операций и
Генераторы такие же независимый насколько это возможно, в том смысле, что между ними нет отношений (опять же в терминах конечных выражений с использованием булевых операций), которые не выполняются в каждый Булева алгебра неважно который элементы выбраны.

Простой пример

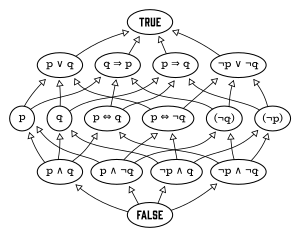
Диаграмма Хассе свободной булевой алгебры с двумя образующими, p и q. Возьмите p (левый кружок), чтобы обозначить «Джон высокий», а q (правый кружок) - «Мэри богата». Атомы - это четыре элемента в строке чуть выше FALSE.

В генераторы свободной булевой алгебры могут представлять независимые предложения. Рассмотрим, например, предложения «Джон высокий» и «Мария богата». Они порождают булеву алгебру с четырьмя атомы, а именно:

Джон высокий, а Мэри богата;
Джон высокий, а Мэри небогат;
Джон невысокий, а Мэри богата;
Джон невысок, а Мэри небогата.

Остальные элементы булевой алгебры тогда логическая дизъюнкция атомов, например: «Джон высокий, а Мария небогатая, или Джон невысокий, а Мария богата». Кроме того, есть еще один элемент, FALSE, который можно рассматривать как пустую дизъюнкцию; то есть дизъюнкция без атомов.

Этот пример дает булеву алгебру с 16 элементами; в общем, для конечных п, свободная булева алгебра с п генераторы имеет 2^п атомы, и поэтому ${ displaystyle 2 ^ {2 ^ {n}}}$ элементы.

Если есть бесконечно много генераторы, аналогичная ситуация преобладает, только сейчас нет атомы. Каждый элемент булевой алгебры представляет собой комбинацию конечного числа порождающих предложений, причем два таких элемента считаются идентичными, если они логически эквивалентный.

Другой способ узнать, почему свободная булева алгебра на множестве n элементов имеет ${ displaystyle 2 ^ {2 ^ {n}}}$ elements следует отметить, что каждый элемент является функцией от n бит до одного. Есть ${ Displaystyle 2 ^ {п}}$ возможных входов для такой функции, и функция выберет 0 или 1 для вывода для каждого входа, поэтому есть ${ displaystyle 2 ^ {2 ^ {n}}}$ возможные функции.

Теоретико-категориальное определение

На языке теория категорий, свободные булевы алгебры могут быть определены просто в терминах примыкание между категорией наборов и функций, Набор, и категория булевых алгебр и гомоморфизмов булевых алгебр, BA. Фактически, этот подход обобщается на любую алгебраическую структуру, определяемую в рамках универсальная алгебра.

Выше мы сказали, что свободная булева алгебра - это булева алгебра с набором генераторов, которые ведут себя определенным образом; как вариант, можно начать с набора и спросить, какую алгебру он порождает. Каждый набор Икс порождает свободную булеву алгебру FX определяется как алгебра такая, что для каждой алгебры B и функция ж : Икс → Bсуществует единственный гомоморфизм булевых алгебр ж′ : FX → B что расширяет ж. Схематически,

куда я_Икс - включение, пунктирная стрелка означает единственность. Идея в том, что как только вы выбираете, куда отправлять элементы Икс, то законы для гомоморфизмов булевых алгебр определить, куда отправить все остальное в свободной алгебре FX. Если FX содержал элементы, невыразимые как комбинации элементов Икс, тогда ж′ Не будет уникальным, и если бы элементы Икс не были достаточно независимыми, тогда ж'Не было бы хорошо определено! Легко показать, что FX единственно (с точностью до изоморфизма), поэтому это определение имеет смысл. Также легко показать, что свободная булева алгебра с порождающим множеством X, как она определена первоначально, изоморфна FX, поэтому два определения согласуются.

Одним из недостатков приведенного выше определения является то, что диаграмма не отражает этого. ж′ - гомоморфизм; так как это диаграмма в Набор каждая стрелка обозначает простую функцию. Мы можем исправить это, разделив его на две диаграммы, одну в BA и один в Набор. Чтобы связать их, мы вводим функтор U : BA → Набор который "забывает "алгебраическая структура, отображение алгебр и гомоморфизмов в их базовые множества и функции.

Если интерпретировать верхнюю стрелку как диаграмму в BA и нижний треугольник в виде диаграммы в Набор, то эта диаграмма правильно выражает, что каждая функция ж : Икс → UB продолжается до единственного гомоморфизма булевых алгебр ж′ : FX → B. Функтор U можно рассматривать как средство для извлечения гомоморфизма ж' назад в Набор так что это может быть связано с ж.

Замечательный аспект этого состоит в том, что последняя диаграмма является одним из различных (эквивалентных) определений того, когда два функтора прилегающий. Наш F легко продолжается до функтора Набор → BA, и наше определение Икс порождающая свободную булеву алгебру FX именно это U имеет левый смежный F.

Топологическая реализация

Свободная булева алгебра с κ генераторы, где κ - конечное или бесконечное количественное числительное, может быть реализована как совокупность всех прищемить подмножества из {0,1}^κ, Учитывая топология продукта предполагая, что {0,1} имеет дискретная топология. Для каждого α <κ величина αth Генератор - это набор всех элементов {0,1}^κ чья αth координата равна 1. В частности, свободная булева алгебра с ${ displaystyle aleph _ {0}}$ генераторы - это собрание всех закрывать подмножества из Канторовское пространство, иногда называемый Алгебра Кантора. Удивительно, но эта коллекция счетный. Фактически, в то время как свободная булева алгебра с п генераторы, п конечный, имеет мощность ${ displaystyle 2 ^ {2 ^ {n}}}$ , свободная булева алгебра с ${ displaystyle aleph _ {0}}$ генераторы, как и для любой свободной алгебры с ${ displaystyle aleph _ {0}}$ генераторы и счетное количество финитарных операций, имеет мощность ${ displaystyle aleph _ {0}}$ .

Подробнее об этом топологический подход к свободной булевой алгебре, см. Теорема Стоуна о представлении булевых алгебр.

Свободная булева алгебра - Free Boolean algebra

Содержание

Простой пример

Теоретико-категориальное определение

Топологическая реализация

Смотрите также

Рекомендации