Магнитный резонанс (квантовая механика) - Википедия - Magnetic resonance (quantum mechanics)
Эта статья нужны дополнительные цитаты для проверка. (Октябрь 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Магнитный резонанс это квантово-механический резонансный эффект, который может появиться при магнитный диполь подвергается статическому магнитное поле и возмущенный другим, колеблющимся электромагнитное поле. Из-за статического поля диполь может принимать ряд дискретных значений энергии собственные состояния, в зависимости от значения его угловой момент квантовое число. Тогда осциллирующее поле может заставить диполь переходить между своими энергетическими состояниями с определенной вероятностью и с определенной скоростью. Общая вероятность перехода будет зависеть от поля частота и ставка будет зависеть от его амплитуда. Когда частота этого поля приводит к максимально возможной вероятности перехода между двумя состояниями, достигается магнитный резонанс. В этом случае энергия фотонов, составляющих осциллирующее поле, соответствует разнице энергий между упомянутыми состояниями. Если на диполь воздействует поле, колеблющееся вдали от резонанса, переход маловероятен. Это аналогично другим резонансным эффектам, таким как принудительный гармонический осциллятор. В периодический переход между разными состояниями называется Цикл Раби и скорость, с которой это происходит, называется Частота Раби. Частоту Раби не следует путать с собственной частотой поля. Поскольку многие атомные ядра может вести себя как магнитный диполь, этот резонансный метод является основой ядерный магнитный резонанс, включая ЯМР-томография и спектроскопия ядерного магнитного резонанса.
Квантово-механическое объяснение
В качестве магнитного диполя, используя вращение система, такая как протон; в соответствии с квантово-механическим состоянием системы, обозначаемым: , возникшие под действием унитарный оператор ; результат подчиняется Уравнение Шредингера:
Состояния с определенной энергией эволюционируют во времени с фазой ,( ) где E - энергия состояния, поскольку вероятность нахождения системы в состоянии = не зависит от времени. Такие состояния называются стационарные состояния, поэтому, если система подготовлена в стационарном состоянии (т. е. в одном из собственных состояний Гамильтонов оператор ), то P (t) = 1, т.е. он остается в этом состоянии неопределенно долго. Это справедливо только для изолированных систем. Когда система в стационарном состоянии возмущается, ее состояние изменяется, поэтому она больше не является собственное состояние полного гамильтониана системы. То же самое явление происходит в магнитном резонансе для вращения система в магнитном поле.
Гамильтониан магнитного диполя (связано с вращением частица) в магнитном поле является:
Здесь это прецессия лармора частота диполя для магнитное поле и это г Матрица Паули. Итак, собственные значения находятся и . Если система возмущена слабым магнитным полем , вращаясь против часовой стрелки в плоскости x-y (перпендикулярно ) с угловой частотой , так что , тогда и не являются собственными состояниями гамильтониана, который преобразован в
Работать с гамильтонианом, зависящим от времени, неудобно. Сделать не зависящий от времени, требует новой системы отсчета, вращающейся с , т.е. оператор вращения на , что составляет базисное изменение Гильбертово пространство. Используя это в уравнении Шредингера, гамильтониан становится:
Письмо в основе в качестве-
Используя эту форму гамильтониана, новый основа находится:
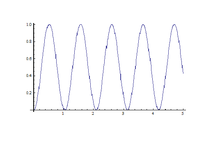

куда и
Этот гамильтониан в точности похож на гамильтониан двухгосударственная система с невозмущенными энергиями & с возмущением, выраженным ; В соответствии с Колебание Раби, начиная с состояние, диполь параллельно с энергией , вероятность того, что он перейдет в состояние (т.е. оно будет перевернуто) равно
Теперь рассмотрим , т.е. поле колеблется с той же скоростью, с которой диполь подвергается воздействию поле делает. Это случай резонанс. Затем в определенные моменты времени, а именно , диполь перевернется, перейдя в другое собственное состояние энергии со 100% вероятностью. Когда , вероятность изменения энергетического состояния мала. Поэтому условие резонанса можно использовать, например, для измерения магнитного момента диполя или магнитного поля в точке в пространстве.
Особый случай для показа приложений
Особый случай возникает, когда система колеблется между двумя нестабильными уровнями, которые имеют одинаковое время жизни. .[1] Если атомы возбуждены с постоянной, скажем, n / раз, до первого состояния, некоторые из них распадаются, а остальные имеют вероятность для перехода во второе состояние, поэтому в интервале времени между t и (t + dt) количество атомов, которые перескакивают во второе состояние из первого, равно , поэтому в момент t количество атомов во втором состоянии равно


=
Скорость распада из состояния два зависит от количества атомов, которые были собраны в этом состоянии за все предыдущие интервалы, поэтому количество атомов в состоянии 2 равно ; Скорость распада атомов из состояния два пропорциональна количеству атомов, присутствующих в этом состоянии, в то время как константа пропорциональности - это константа распада. . Выполнение интегрирования скорости распада атомов из состояния два получается как:
Из этого выражения можно извлечь много интересных моментов, например
- Изменяющееся однородное магнитное поле так что в дает кривую Лоренца (см. Распределение Коши – Лоренца ), обнаружив пик этой кривой, абсцисса из этого дает , а сейчас (угловая частота вращения = , поэтому из известного значения и , гиромагнитное отношение диполя можно измерить; этим методом мы можем измерить Ядерный спин где все электронные вращения сбалансированы. Правильное измерение ядерный магнитный момент помогает понять характер ядерной силы.
- Если известно, варьируя , значение может быть получен. Этот метод измерения достаточно точен для использования в чувствительных магнитометрах. Используя этот метод, можно получить значение магнитного поля, действующего на определенный узел решетки окружающей средой внутри кристалла.
- Измеряя полуширину кривой, d =, для нескольких значений (т.е. ), мы можем построить d vs , и экстраполируя эту строку на время жизни нестабильных состояний может быть получено из перехвата.
Метод Раби

Существование спинового углового момента электронов было экспериментально обнаружено Эксперимент Штерна-Герлаха. В этом исследовании пучок нейтральных атомов с одним электроном в валентной оболочки, не несущий орбитального момента (с точки зрения квантовой механики), пропускался через неоднородное магнитное поле. Этот процесс не был приблизительным из-за малого угла отклонения, что приводило к значительной погрешности в измеренном значении расщепленной балки.
Метод Раби был улучшением по сравнению с методом Штерна-Герлаха. Как показано на рисунке, источник испускает пучок нейтральных атомов, имеющих спиновый угловой момент . Луч проходит через серию из трех выровненных магнитов. Магнит 1 создает неоднородное магнитное поле с большим градиентом(как у Штерна-Герлаха), поэтому атомы, имеющие `` восходящий '' спин (с ) отклонится вниз (путь 1), т.е. в область меньшего магнитного поля B, чтобы минимизировать энергию. Атомы со спином «вниз» с ) аналогично отклонится вверх (путь 2). Лучи проходят через щель 1, чтобы уменьшить влияние источника за ее пределами. Магнит 2 создает только однородное магнитное поле в вертикальном направлении, не прикладывая силы к атомному пучку, а магнит 3 фактически является перевернутым магнитом 1. В области между полюсами магнита 3 атомы, имеющие «направленный вверх» спин, толкаются вверх, и атомы имеющие «нисходящее» вращение ощущают толчок вниз, поэтому их путь остается 1 и 2 соответственно. Эти лучи проходят через вторую щель S2, попадают в детектор и обнаруживаются.
Если горизонтальное вращающееся поле , угловая частота вращения применяется в области между полюсами магнита 2, создаваемого колеблющимся током в кольцевых катушках, тогда существует вероятность того, что атомы проходят через них из одного спинового состояния в другое ( и наоборот), когда =, Ларморова частота прецессии магнитного момента в B.[требуется разъяснение ] Атомы, которые переходят от «восходящего» к «нисходящему» спину, будут испытывать нисходящую силу при прохождении через магнит 3 и будут следовать по пути 1 ». Точно так же атомы, которые меняют вращение «вниз» на «вверх», будут следовать по пути 2, и эти атомы не достигнут детектора, что приведет к минимуму в детекторе. Если угловая частота из изменяется непрерывно, то будет получен минимум тока детектора (когда =). Из этого известного значения (, где g - 'Земельные участки é фактор g '), Получен g-фактор Ланде, который позволит получить правильное значение магнитного момента . Этот эксперимент, проведенный Исидор Исаак Раби более чувствителен и точен по сравнению с Stern-Gerlach.
Соответствие классического и квантово-механического объяснений
Хотя понятие спиновый угловой момент возникает только в квантовой механике и не имеет классического аналога, явления магнитного резонанса можно до некоторой степени объяснить с помощью классической физики. Если смотреть из системы отсчета, прикрепленной к вращающемуся полю, кажется, что магнитный диполь прецессирует вокруг чистого магнитного поля. , куда - единичный вектор вдоль однородного магнитного поля и то же самое в направлении вращающегося поля и .
Доказательство классического выражения прецессии 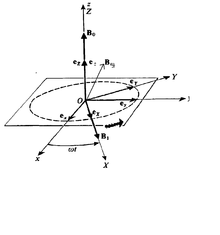 Графическое изображение классической ларморовской прецессии
Графическое изображение классической ларморовской прецессииКлассическая электродинамика говорит нам, что крутящий момент на магнитном диполе момента является × , поэтому его уравнение движения
× , (куда угловой момент, связанный с диполем), так что -
- ×
Для рассматриваемого случая диполь находится под действием магнитного поля и , следовательно
× Ее проще решить, преобразовав систему координат в OXYZ, в которой становится осью OX, в этом кадре -
×
здесь С помощью и , видно, что-
- ×× ( )
Итак, здесь эффективное поле становится:
Так когда , большая амплитуда прецессии позволяет полностью перевернуть магнитный момент. Классические и квантово-механические предсказания хорошо соответствуют, что можно рассматривать как пример Боровская переписка принцип, который гласит, что квантово-механические явления, предсказанные в классическом режиме, должны соответствовать классическому результату. Происхождение этого соответствия состоит в том, что эволюция ожидаемого значения магнитного момента идентична полученной с помощью классических рассуждений. Ожидаемое значение магнитного момента равно . Временная эволюция дан кем-то
так,
Так, и
которое выглядит точно так же, как уравнение движения магнитного момента в классической механике -
Эта аналогия в математическом уравнении эволюции магнитного момента и его математического ожидания помогает понять явления без фона квантовой механики.
Магнитно-резонансная томография
В магнитно-резонансной томографии (МРТ) используется спиновый угловой момент протона. Самый доступный источник протонов - атомы водорода в воде. Сильное магнитное поле применительно к воде вызывает появление двух различных уровней энергии для спинового углового момента - () и -(), с помощью .
Согласно Распределение Больцмана (количество систем, имеющих энергию снаружи при температуре ) является (где k Постоянная Больцмана ) более низкий уровень энергии, связанный со спином более населенный, чем другой. В присутствии вращающегося магнитного поля больше протонов переворачивается из к чем перевернуть в другую сторону, вызывая поглощение микроволнового или радиоволнового излучения (от вращающегося поля). Когда поле снимается, протоны стремятся повторно уравновеситься по распределению Больцмана, поэтому некоторые протоны переходят с более высокого энергетического уровня на более низкий, испуская микроволновое или радиоволновое излучение на определенных частотах.
Вместо ядерного спина в ЭПР используется спиновый угловой момент неспаренных электронов (Электронный парамагнитный резонанс ) для обнаружения свободных радикалов и т. д.
Магнитный резонанс как квантовое явление
Явление магнитного резонанса коренится в существовании спинового углового момента квантовой системы и ее специфической ориентации по отношению к приложенному магнитному полю. Оба случая не имеют объяснения в классическом подходе и могут быть поняты только с помощью квантовой механики. Некоторые люди утверждают[ВОЗ? ] что чисто квантовые явления не могут быть объяснены классическим подходом. Например, явления в микроскопической области, которые можно до некоторой степени описать классической аналогией, на самом деле не являются квантовыми явлениями. Поскольку основные элементы магнитного резонанса не имеют классического происхождения, хотя можно провести аналогию с Классическим Ларморова прецессия, MR следует рассматривать как квантовое явление.
Смотрите также
- Ядерный магнитный резонанс
- Магнитно-резонансная томография
- Уравнения Блоха
- Физика магнитно-резонансной томографии
Рекомендации
- ^ Страница 449, Квантовая механика, Том 1, Клод Коэн-Таннуджи, Бернар Диу, Фрэнк Лало
- Фейнман, Лейтон, Пески. Лекции Фейнмана по физике, том 3. Издательство Нароса, Нью-Дели, 2008.CS1 maint: несколько имен: список авторов (связь)
- Коэн-Таннуджи Клод. Квантовая механика. Wiley-VCH.
- Гриффитс Дэвид Дж. Введение в квантовую механику. Pearson Education, Inc.


































![{ displaystyle P_ {12} = { frac {| omega _ {1} ^ {2} |} {| Delta omega ^ {2} + omega _ {1} ^ {2} |}} грех ^ {2} [{ sqrt { omega ^ {2} + Delta omega ^ {2}}} t / 2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1309c8161e11cdf6c586e43c91421f126744486b)



















































![{ displaystyle i hbar { frac {d} {dt}} langle mathbf {m} rangle = langle [ mathbf {m}, { hat {H}}] rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fa60b86ed962223f0d88fb9c3ddc0849db01532)

![{ displaystyle [m_ {i}, { hat {H}}] = [m_ {i}, - m_ {j} B_ {j}] = [ gamma mathbf {S} _ {i}, - гамма mathbf {S} _ {j} mathbf {B} _ {j}] = - gamma ^ {2} [ mathbf {S} _ {i}, mathbf {S} _ {j} mathbf {B} _ {j}] = - gamma ^ {2} i hbar [{ mathbf {S} _ {k} mathbf {B} _ {j} - mathbf {S} _ {j} mathbf {B} _ {k}}], (я neq j, k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90c1acbee460a9f8d8a5d38be7f173ec76bdb789)
![{ displaystyle [m_ {i}, { hat {H}}] = i hbar gamma [ mathbf {B} _ {j} mathbf {m} _ {k} - mathbf {B} _ { к} mathbf {m} _ {j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2526c1ab271d9023e4bb6b378754c0ca512ab7d5)










