Многокритериальный анализ решений - Multiple-criteria decision analysis

Принятие решений по нескольким критериям (MCDM) или многокритериальный анализ решений (MCDA) является суб-дисциплиной исследование операций который явно оценивает несколько конфликтующих критерии в принятие решений (как в повседневной жизни, так и в таких условиях, как бизнес, правительство и медицина). При оценке вариантов типичны противоречивые критерии: Стоимость или цена обычно является одним из основных критериев, и некоторая мера качества обычно является другим критерием, который легко вступает в противоречие со стоимостью. При покупке автомобиля стоимость, комфорт, безопасность и экономия топлива могут быть одними из основных критериев, которые мы принимаем во внимание - необычно, что самый дешевый автомобиль является наиболее удобным и безопасным. В Управление портфелем менеджеры заинтересованы в получении высокой доходности при одновременном снижении рисков; однако акции, которые могут принести высокую прибыль, обычно несут в себе высокий риск потери денег. В сфере услуг удовлетворенность клиентов и стоимость предоставления услуг являются фундаментальными противоречивыми критериями.
В своей повседневной жизни люди обычно неявно взвешивают несколько критериев и могут быть довольны последствиями таких решений, которые принимаются только на основе интуиция.[1] С другой стороны, когда ставки высоки, важно правильно структурировать проблему и явно оценить несколько критериев.[2] При принятии решения о том, строить атомную электростанцию или нет и где ее строить, возникают не только очень сложные вопросы, связанные с множеством критериев, но также есть множество сторон, на которых серьезно влияют последствия.
Хорошая структуризация сложных проблем и учет нескольких критериев явно приводит к более информированным и лучшим решениям. В этой области были достигнуты важные успехи с момента появления современной дисциплины принятия решений по множественным критериям в начале 1960-х годов. Разнообразные подходы и методы, многие из которых реализованы специализированными программное обеспечение для принятия решений,[3][4] были разработаны для их применения во множестве дисциплин, от политики и бизнеса до окружающей среды и энергетики.[5]
Основы, концепции, определения
MCDM или MCDA - хорошо известные аббревиатуры для многокритериальное принятие решений и многокритериальный анализ решений; Стэнли Зионтс способствовал популяризации аббревиатуры своей статьей 1979 года «MCDM - Если не римская цифра, то что?», Предназначенной для предпринимательской аудитории.
MCDM занимается структурированием и решением проблем принятия решений и планирования с использованием нескольких критериев. Цель состоит в том, чтобы поддержать лиц, принимающих решения, перед лицом таких проблем. Как правило, не существует уникального оптимальный решение таких проблем, и необходимо использовать предпочтения лица, принимающего решения, чтобы различать решения.
«Решение» можно трактовать по-разному. Это может соответствовать выбору «лучшей» альтернативы из набора доступных альтернатив (где «лучший» может интерпретироваться как «наиболее предпочтительная альтернатива» лица, принимающего решение). Другая интерпретация «решения» может заключаться в выборе небольшого набора хороших альтернатив или группировании альтернатив в различные наборы предпочтений. Крайняя интерпретация может заключаться в том, чтобы найти все «эффективные» или «недоминированный альтернативы (которые мы вскоре определим).
Сложность проблемы проистекает из наличия более чем одного критерия. Больше не существует единственного оптимального решения проблемы MCDM, которое можно было бы получить без включения информации о предпочтениях. Концепция оптимального решения часто заменяется набором недоминируемых решений. Недоминируемое решение обладает тем свойством, что от него невозможно перейти к любому другому решению, не жертвуя хотя бы одним критерием. Следовательно, для лица, принимающего решение, имеет смысл выбрать решение из недоминируемого набора. В противном случае он / она могли бы добиться большего успеха по некоторым или всем критериям и не добиться худших результатов по любому из них. Однако обычно набор недоминируемых решений слишком велик, чтобы их можно было представить лицу, принимающему решение, для окончательного выбора. Следовательно, нам нужны инструменты, которые помогают лицам, принимающим решения, сосредоточиться на предпочтительных решениях (или альтернативах). Обычно приходится «менять» одни критерии на другие.
MCDM является активной областью исследований с 1970-х годов. Есть несколько организаций, связанных с MCDM, включая Международное общество по принятию решений по нескольким критериям,[6] Европейская рабочая группа по ВРСГО,[7] и раздел ИНФОРМАЦИЯ по MCDM.[8] Историю см .: Köksalan, Wallenius and Zionts (2011).[9]MCDM опирается на знания во многих областях, включая:
Типология
Существуют разные классификации задач и методов MCDM. Основное различие между проблемами MCDM основано на том, определены ли решения явно или неявно.
- Проблемы многокритериальной оценки: Эти проблемы состоят из конечного числа альтернатив, явно известных в начале процесса решения. Каждая альтернатива представлена своей производительностью по нескольким критериям. Проблема может быть определена как поиск лучшей альтернативы для лица, принимающего решения (ЛПР), или поиск набора хороших альтернатив. Также может быть интересна «сортировка» или «классификация» альтернатив. Сортировка означает размещение альтернатив в наборе упорядоченных по предпочтениям классов (например, присвоение кредитных рейтингов странам), а классификация относится к назначению альтернатив неупорядоченным наборам (например, диагностика пациентов на основе их симптомов). Некоторые методы MCDM в этой категории были сравнительно изучены в книге Триантафиллоу по этому вопросу, 2000.[10]
- Многокритериальные задачи проектирования (многокритериальные задачи математического программирования): В этих задачах альтернативы явно не известны. Альтернативу (решение) можно найти, решив математическую модель. Число альтернатив либо бесконечно и не счетно (когда некоторые переменные непрерывны), либо обычно очень велико, если счетное (когда все переменные дискретны).
Независимо от того, является ли это проблемой оценки или проблемой дизайна, требуется информация о предпочтениях DM, чтобы различать решения. Способы решения проблем MCDM обычно классифицируются на основе времени получения информации о предпочтениях от DM.
Существуют методы, которые требуют информации о предпочтениях DM в начале процесса, превращая проблему по существу в проблему с одним критерием. Утверждается, что эти методы действуют путем «предварительного определения предпочтений». Методы, основанные на оценке функции ценности или использовании концепции «превосходящих отношений», процесса аналитической иерархии и некоторых методов, основанных на правилах принятия решений, пытаются решить задачи оценки по множеству критериев, используя предварительную формулировку предпочтений. Точно так же существуют методы, разработанные для решения задач проектирования с несколькими критериями с использованием предварительного определения предпочтений путем построения функции ценности. Возможно, наиболее известным из этих методов является целевое программирование. Как только функция ценности построена, полученная единственная целевая математическая программа решается для получения предпочтительного решения.
Некоторые методы требуют информации о предпочтениях от DM на протяжении всего процесса решения. Они называются интерактивными методами или методами, требующими «прогрессивной формулировки предпочтений». Эти методы были хорошо разработаны как для оценки множественных критериев (см., Например, Geoffrion, Dyer and Feinberg, 1972,[11] и Коксалан и Сагала, 1995 г.[12] ) и проектные проблемы (см. Steuer, 1986[13]).
Задачи многокритериального проектирования обычно требуют решения ряда моделей математического программирования, чтобы выявить неявно определенные решения. Для этих проблем также может представлять интерес представление или приближение «эффективных решений». Эта категория называется «апостериорной артикуляцией предпочтений», подразумевая, что участие DM начинается после явного раскрытия «интересных» решений (см., Например, Karasakal and Köksalan, 2009[14]).
Когда модели математического программирования содержат целочисленные переменные, проблемы проектирования становится труднее решать. Многокритериальная комбинаторная оптимизация (MOCO) составляет особую категорию таких задач, вызывающих существенные вычислительные трудности (см. Ehrgott and Gandibleux,[15] 2002, для обзора).
Представления и определения
Проблема MCDM может быть представлена в пространстве критериев или пространстве решений. В качестве альтернативы, если различные критерии комбинируются с помощью взвешенной линейной функции, также возможно представить проблему в пространстве весов. Ниже приведены демонстрации критериального и весового пространств, а также некоторые формальные определения.
Представление в пространстве критериев
Допустим, мы оцениваем решения в конкретной проблемной ситуации по нескольким критериям. Далее предположим, что чем больше, тем лучше по каждому критерию. Тогда среди всех возможных решений мы в идеале заинтересованы в тех решениях, которые хорошо работают по всем рассматриваемым критериям. Однако вряд ли будет какое-то одно решение, которое хорошо работает по всем рассматриваемым критериям. Как правило, некоторые решения хорошо работают по одним критериям, а некоторые - по другим. Поиск способа компромисса между критериями - одна из основных задач в литературе MCDM.
Математически задача MCDM, соответствующая приведенным выше аргументам, может быть представлена как
- "Максимум" q
- при условии
- q ∈ Q
где q вектор k критериальные функции (целевые функции) и Q допустимый набор, Q ⊆ рk.
Если Q определяется явно (набором альтернатив), результирующая задача называется задачей оценки по нескольким критериям.
Если Q определяется неявно (набором ограничений), результирующая задача называется многокритериальной задачей проектирования.
Кавычки используются, чтобы указать, что максимизация вектора не является четко определенной математической операцией. Это соответствует аргументу о том, что нам придется найти способ разрешить компромисс между критериями (обычно на основе предпочтений лица, принимающего решения), когда не существует решения, которое хорошо работает по всем критериям.
Представление пространства решений
Пространство решений соответствует набору возможных решений, доступных нам. Значения критериев будут последствиями принимаемых нами решений. Следовательно, мы можем определить соответствующую проблему в пространстве решений. Например, при разработке продукта мы выбираем параметры дизайна (переменные решения), каждый из которых влияет на показатели (критерии) производительности, с помощью которых мы оцениваем наш продукт.
Математически задача проектирования с несколькими критериями может быть представлена в пространстве решений следующим образом:
где Икс допустимый набор и Икс - вектор решающей переменной размера n.
Хорошо разработанный частный случай получается, когда Икс является многогранником, определяемым линейными неравенствами и равенствами. Если все целевые функции являются линейными с точки зрения переменных решения, это изменение приводит к множественному целевому линейному программированию (MOLP), важному подклассу задач MCDM.
Есть несколько определений, которые занимают центральное место в MCDM. Два тесно связанных определения - это недоминантность (определенная на основе представления пространства критериев) и эффективность (определенная на основе представления переменной решения).
Определение 1. д * ∈ Q не назначается, если не существует другого q ∈ Q такой, что q ≥ д * и q ≠ д *.
Грубо говоря, решение не считается доминирующим, если оно не уступает любому другому доступному решению по всем рассматриваемым критериям.
Определение 2. Икс* ∈ Икс эффективен, если не существует другого Икс ∈ Икс такой, что ж(Икс) ≥ ж(Икс*) и ж(Икс) ≠ ж(Икс*).
Если проблема MCDM хорошо представляет ситуацию принятия решения, то наиболее предпочтительным решением DM должно быть эффективное решение в пространстве решений, а его изображение - недоминируемая точка в пространстве критериев. Следующие определения также важны.
Определение 3. д * ∈ Q слабо не доминирует, если не существует другого q ∈ Q такой, что q > д *.
Определение 4. Икс* ∈ Икс слабоэффективен, если не существует другого Икс ∈ Икс такой, что ж(Икс) > ж(Икс*).
Слабо недоминированные точки включают все недоминируемые точки и некоторые особые доминируемые точки. Важность этих особых доминируемых точек проистекает из того факта, что они обычно появляются на практике, и необходимо особое внимание, чтобы отличить их от недоминируемых точек. Если, например, мы максимизируем единственную цель, мы можем получить слабо недоминируемую точку, над которой доминируют. Доминируемые точки слабо недоминируемого множества расположены либо на вертикальной, либо на горизонтальной плоскостях (гиперплоскостях) в пространстве критериев.
Идеальная точка: (в пространстве критериев) представляет лучшее (максимум для задач максимизации и минимум для задач минимизации) каждой целевой функции и обычно соответствует недопустимому решению.
Точка Надир: (в пространстве критериев) представляет наихудшую (минимум для задач максимизации и максимум для задач минимизации) каждой целевой функции среди точек в недоминируемом наборе и обычно является доминирующей точкой.
Идеальная точка и точка надира полезны мастеру, чтобы получить «ощущение» диапазона решений (хотя найти точку надира для задач проектирования, имеющих более двух критериев, непросто).
Иллюстрации пространств решений и критериев
Следующая задача MOLP с двумя переменными в пространстве переменных решения поможет продемонстрировать некоторые ключевые концепции графически.

На рисунке 1 крайние точки «е» и «b» максимизируют первую и вторую цели соответственно. Красная граница между этими двумя крайними точками представляет собой эффективный набор. Из рисунка видно, что для любого допустимого решения за пределами эффективного набора можно улучшить обе цели на несколько пунктов в эффективном наборе. И наоборот, для любой точки эффективного набора невозможно улучшить обе цели, переходя к любому другому допустимому решению. При таких решениях нужно жертвовать одной из целей, чтобы улучшить другую.
Из-за своей простоты указанная выше проблема может быть представлена в пространстве критериев путем замены Иксс с ж с следующим образом:

- Максимум ж1
- Максимум ж2
- при условии
- ж1 + 2ж2 ≤ 12
- 2ж1 + ж2 ≤ 12
- ж1 + ж2 ≤ 7
- ж1 – ж2 ≤ 9
- −ж1 + ж2 ≤ 9
- ж1 + 2ж2 ≥ 0
- 2ж1 + ж2 ≥ 0
Мы представляем пространство критериев графически на рисунке 2. В пространстве критериев легче обнаружить недоминируемые точки (соответствующие эффективным решениям в пространстве решений). Северо-восточная область допустимого пространства представляет собой набор недоминируемых точек (для задач максимизации).
Создание недоминированных решений
Есть несколько способов генерировать недоминированные решения. Мы обсудим два из них. Первый подход может генерировать особый класс недоминируемых решений, тогда как второй подход может генерировать любое недоминируемое решение.
- Взвешенные суммы (Гасс и Саати, 1955 г.[16])
Если мы объединим несколько критериев в один критерий, умножив каждый критерий на положительный вес и суммируя взвешенные критерии, то решение результирующей проблемы с одним критерием станет специальным эффективным решением. Эти специальные эффективные решения появляются в угловых точках множества доступных решений. Эффективные решения, не находящиеся в угловых точках, обладают особыми характеристиками, и этот метод не может найти такие точки. Математически мы можем представить эту ситуацию как
- Максимум шТ.q = шТ.f (x), ш> 0
- при условии
- Икс ∈ Икс
Варьируя веса, взвешенные суммы могут использоваться для генерации эффективных решений экстремальных точек для задач проектирования и поддерживаемых (выпуклых недоминируемых) точек для задач оценки.
- Функция скаляризации достижений (Вежбицкий, 1980[17])
Функции скаляризации достижений также объединяют несколько критериев в один критерий, взвешивая их особым образом. Они создают прямоугольные контуры, уходящие от ориентира в сторону доступных эффективных решений. Эта специальная структура позволяет функциям масштабирования достижений находить любое эффективное решение. Это мощное свойство, которое делает эти функции очень полезными для задач MCDM.
Математически мы можем представить соответствующую задачу в виде
- Мин. s(г, д, ш, ρ) = Мин Макся [(граммя − qя)/шя ] + ρ ∑я (граммя − qя)},
- при условии
- q ∈ Q
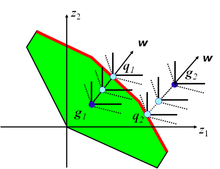
Функция масштабирования достижений может использоваться для проецирования любой точки (выполнимой или недопустимой) на границе эффективности. Любая точка (поддерживаемая или нет) может быть достигнута. Второй член целевой функции необходим, чтобы избежать неэффективных решений. Рисунок 3 демонстрирует, как возможная точка, грамм1, и недопустимая точка, грамм2, проецируются на недоминируемые точки, q1 и q2соответственно по направлению ш с использованием функции масштабирования достижений. Пунктирные и сплошные контуры соответствуют контурам целевой функции со вторым членом целевой функции и без него соответственно.
Решение проблем MCDM
Для решения задач MCDM (как дизайна, так и оценочного типа) сложились разные школы. Библиометрическое исследование, показывающее их развитие с течением времени, см. В Bragge, Korhonen, H. Wallenius и J. Wallenius [2010].[18]
Школа многоцелевого математического программирования
(1) Максимизация вектора: Цель максимизации вектора - аппроксимировать недоминируемый набор; первоначально был разработан для задач линейного программирования с несколькими объектами (Evans, Steuer, 1973;[19] Ю и Зеленый, 1975[20]).
(2) Интерактивное программирование: Фазы вычислений чередуются с фазами принятия решений (Benayoun et al., 1971;[21] Джеффрион, Дайер и Файнберг, 1972;[22] Зионты и Валлениус, 1976;[23] Корхонен и Валлениус, 1988 г.[24]). Не предполагается явного знания функции ценности DM.
Цель состоит в том, чтобы установить априорные целевые значения для целей и минимизировать взвешенные отклонения от этих целей. Использовались как веса важности, так и лексикографические упреждающие веса (Charnes, Cooper, 1961).[25]).
Теоретики нечетких множеств
Нечеткие множества были введены Заде (1965).[26] как расширение классического понятия множеств. Эта идея используется во многих алгоритмах MCDM для моделирования и решения нечетких задач.
Теоретики мультиатрибутной полезности
Утилита с несколькими атрибутами или функции значения извлекаются и используются для определения наиболее предпочтительной альтернативы или для ранжирования альтернатив. Используются сложные методы интервью, которые существуют для выявления линейных аддитивных функций полезности и мультипликативных нелинейных функций полезности (Keeney and Raiffa, 1976[27]).
Французская школа
Французская школа фокусируется на помощи в принятии решений, в частности ЭЛЕКТРА семейство методов оценки результатов, появившееся во Франции в середине 1960-х годов. Метод был впервые предложен Бернардом Роем (Roy, 1968[28]).
Школа эволюционной многокритериальной оптимизации (EMO)
Алгоритмы EMO начинаются с начальной популяции и обновляют ее, используя процессы, разработанные для имитации естественных принципов выживания наиболее приспособленных и операторов генетической вариации, чтобы улучшить среднюю популяцию от одного поколения к другому. Цель состоит в том, чтобы сойтись к совокупности решений, которые представляют недоминируемое множество (Schaffer, 1984;[29] Шринивас и Деб, 1994[30]). В последнее время предпринимаются попытки включить информацию о предпочтениях в процесс решения алгоритмов EMO (см. Deb and Köksalan, 2010[31]).
Теория серых систем основанные методы
В 1980-х годах Дэн Джулонг предложила теорию системы Грея (GST) и свою первую модель принятия решений с множеством атрибутов, названную Deng's Серый реляционный анализ (GRA) модель. Позже исследователи серых систем предложили множество методов на основе GST, таких как Лю Шифэн модель Absolute GRA,[32] Принятие решений с серой целью (GTDM)[33] и Grey Absolute Decision Analysis (GADA).[34]
Процесс аналитической иерархии (AHP)
AHP сначала разбивает проблему решения на иерархию подзадач. Затем лицо, принимающее решение, оценивает относительную важность различных его элементов путем попарных сравнений. AHP преобразует эти оценки в числовые значения (веса или приоритеты), которые используются для расчета баллов для каждой альтернативы (Saaty, 1980).[35]). Индекс согласованности измеряет степень последовательности ответов лица, принимающего решения. AHP - один из наиболее спорных методов, перечисленных здесь, некоторые исследователи из сообщества MCDA считают его ошибочным.[нужна цитата ]. Основная математика также более сложна[нечеткий ], хотя он приобрел некоторую популярность благодаря коммерчески доступному программному обеспечению.
В нескольких статьях рассматривается применение методов MCDM в различных дисциплинах, таких как нечеткая MCDM,[36] классический MCDM,[37] устойчивая и возобновляемая энергия,[38] Техника ВИКОР,[39] транспортные системы,[40] качество обслуживания,[41] Метод ТОПСИС,[42] проблемы энергоменеджмента,[43] электронное обучение,[44] туризм и гостеприимство,[45] Методы SWARA и WASPAS.[46]
MCDM методы
Доступны следующие методы MCDM, многие из которых реализуются специализированными программное обеспечение для принятия решений:[3][4]
- Метод рандомизации агрегированных индексов (AIRM)
- Аналитическая иерархия процессов (AHP)
- Аналитический сетевой процесс (ANP)
- Процесс балансировки балки
- Метод базовых критериев (BCM)[47]
- Лучший худший метод (BWM)[48][49]
- Модель Брауна – Гибсона
- Характерные объекты МЕТОД (КОМЕТА)[50][51]
- Выбор по преимуществам (CBA)
- Анализ охвата данных
- Решение EXpert (DEX)
- Дезагрегация - подходы к агрегированию (UTA *, UTAII, UTADIS)
- Грубый набор (Приближенный подход)
- Подход, основанный на доминировании (DRSA)
- ЭЛЕКТРА (Превышение рейтинга)
- Оценка на основе расстояния от среднего решения (EDAS)[52]
- Доказательный подход к рассуждению (ER)
- Программирование целей (GP)
- Серый реляционный анализ (GRA)
- Внутреннее произведение векторов (IPV)
- Оценка привлекательности с помощью категориальной методики оценки (МАКБЕТ)
- Простая методика оценки по нескольким атрибутам (УМНЫЙ) [53]
- Стратифицированное принятие решений по нескольким критериям (SMCDM)
- Мультиатрибутный глобальный вывод качества (MAGIQ)
- Теория мультиатрибутной полезности (MAUT)
- Теория многоатрибутных значений (MAVT)
- Марковское принятие решений по нескольким критериям
- Новый подход к оценке (НАТА)
- Неструктурная система поддержки нечетких решений (NSFDSS)
- Потенциально все попарные ранжирования всех возможных альтернатив (ПАПРИКА)
- ПРОМЕТИ (Превышение рейтинга)
- Рейтинг на основе оптимальных баллов (RBOP)[54]
- Стохастический многокритериальный анализ приемлемости (SMAA)
- Метод ранжирования превосходства и неполноценности (Метод SIR)
- Методика расстановки приоритетов по подобию идеальному решению (ТОПСИС)
- Анализ стоимости (ВА)
- Разработка стоимости (VE)
- ВИКОР метод[55]
- Взвешенная модель продукта (WPM)
- Модель взвешенной суммы (WSM)
- Modelo Integrado de Valor para Estructuras Sostenibles (MIVES)[56][57]
Смотрите также
- Метод анализа компромиссов в архитектуре
- Принятие решений
- ПО для принятия решений
- Парадокс принятия решений
- Решающий баланс
- Проблемы многокритериальной классификации
- Смена рангов при принятии решений
- Метод ранжирования превосходства и неполноценности
Рекомендации
- ^ Рью, Л. (1988). «Интуиция в принятии решений». Журнал стипендий по сестринскому делу. 20 (3): 150–154. Дои:10.1111 / j.1547-5069.1988.tb00056.x. PMID 3169833.
- ^ Franco, L.A .; Монтибеллер, Г. (2010). «Структурирование проблем для вмешательств по многокритериальному анализу решений». Энциклопедия исследований операций и управления Wiley. Дои:10.1002 / 9780470400531.eorms0683. ISBN 9780470400531.
- ^ а б Вайстроффер, Х. Р., Смит, К. Х. и Нарула, С. С., «Программное обеспечение для поддержки принятия решений по множеству критериев», глава 24 в: Фигейра, Дж., Греко, С., и Эрготт, М., ред., Анализ принятия решений по множественным критериям: серия обзоров современного состояния, Springer: Нью-Йорк, 2005.
- ^ а б Макгинли, П. (2012), «Обзор программного обеспечения для анализа решений», ИЛИ / MS сегодня, 39, в архиве из оригинала 28 марта 2013 г..
- ^ Килили, Анжелики; Кристофору, Элиас; Fokaides, Paris A .; Поликарпу, Поликарпос (2016). «Многокритериальный анализ для выбора наиболее подходящих энергетических культур: пример Кипра». Анжелики Килили, Элиас Христофору, Пэрис А. Фокайдес, Поликарпос Поликарпу. 35 (1): 47–58. Bibcode:2016IJSE ... 35 ... 47K. Дои:10.1080/14786451.2014.898640. S2CID 108512639.
- ^ «Принятие решений по множеству критериев - Международное общество по MCDM». www.mcdmsociety.org. В архиве из оригинала 3 октября 2017 г.. Получено 26 апреля 2018.
- ^ «Добро пожаловать на сайт EWG-MCDA». www.cs.put.poznan.pl. В архиве из оригинала 7 октября 2017 г.. Получено 26 апреля 2018.
- ^ «Архивная копия». Архивировано из оригинал 11 августа 2011 г.. Получено 7 августа 2011.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
- ^ Коксалан, М., Валлениус, Дж., И Зионц, С. (2011). Принятие решений по множеству критериев: от ранней истории до 21 века. Сингапур: World Scientific. ISBN 9789814335591.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ Триантафиллу, Э. (2000). Принятие многокритериальных решений: сравнительное исследование. Дордрехт, Нидерланды: Kluwer Academic Publishers (ныне Springer). п. 320. ISBN 978-0-7923-6607-2. В архиве из оригинала от 24 июня 2010 г.
- ^ Интерактивный подход к многокритериальной оптимизации с приложением к работе академического отдела, A. М. Джеффрион, Дж. С. Дайер и А. Файнберг, Наука управления, Vol. 19, No. 4, Application Series, Part 1 (декабрь 1972 г.), стр. 357–368 Опубликовано: INFORMS
- ^ Коксалан, М. и Sagala, P.N.S., M. M .; Сагала, П. Н. С. (1995). «Интерактивные подходы к дискретному альтернативному принятию решений по множеству критериев с монотонными функциями полезности». Наука управления. 41 (7): 1158–1171. Дои:10.1287 / mnsc.41.7.1158.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ Steuer, R.E. (1986). Оптимизация по нескольким критериям: теория, вычисления и применение. Нью-Йорк: Джон Вили.
- ^ Карасакал, Э. К. и Коксалан, М., Э .; Коксалан, М. (2009). «Создание репрезентативного подмножества эффективных границ в принятии решений по множеству критериев». Исследование операций. 57: 187–199. Дои:10.1287 / opre.1080.0581.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ Эрготт, М., Гандибле, X. (2002). «Многоцелевая комбинаторная оптимизация». Оптимизация по нескольким критериям, современные аннотированные библиографические обзоры: 369–444. Цитировать журнал требует
| журнал =(Помогите) - ^ Gass, S .; Саати, Т. (1955). «Параметрическая целевая функция, часть II». Исследование операций. 2 (3): 316–319. Дои:10.1287 / opre.2.3.316.
- ^ Вежбицкий, А. (1980). «Использование эталонных целей в многокритериальной оптимизации». Теория и применение множественных критериев принятия решений. Конспект лекций по экономике и математическим системам. Спрингер, Берлин. 177. С. 468–486. Дои:10.1007/978-3-642-48782-8_32. ISBN 978-3-540-09963-5.
- ^ Bragge, J .; Korhonen, P .; Валлениус, H .; Валлениус Дж. (2010). Библиометрический анализ принятия решений по множественным критериям / теория множественной полезности. Материалы конференции IXX International MCDM, (ред.) М. Эрготт, Б. Науйокс, Т. Стюарт и Дж. Валлениус. Спрингер, Берлин. 634. С. 259–268. Дои:10.1007/978-3-642-04045-0_22. ISBN 978-3-642-04044-3.
- ^ Evans, J .; Steuer, R. (1973). «Пересмотренный симплекс-метод для линейных многоцелевых программ». Математическое программирование. 5: 54–72. Дои:10.1007 / BF01580111. S2CID 32037123.
- ^ Ю. П.Л .; Зеленый, М. (1975). «Множество всех недоминируемых решений в линейных случаях и многокритериальный симплекс-метод». Журнал математического анализа и приложений. 49 (2): 430–468. Дои:10.1016 / 0022-247X (75) 90189-4.
- ^ Benayoun, R .; deMontgolfier, J .; Tergny, J .; Ларичев, О. (1971). «Линейное программирование с несколькими целевыми функциями: пошаговый метод (STEM)». Математическое программирование. 1: 366–375. Дои:10.1007 / bf01584098. S2CID 29348836.
- ^ Джеффрион, А .; Dyer, J .; Файнберг, А. (1972). «Интерактивный подход к многокритериальной оптимизации с приложением к работе академического отдела». Наука управления. 19 (4 – Часть – 1): 357–368. Дои:10.1287 / mnsc.19.4.357.
- ^ Zionts, S .; Валлениус Дж. (1976). «Интерактивный метод программирования для решения проблемы множественных критериев». Наука управления. 22 (6): 652–663. Дои:10.1287 / mnsc.22.6.652.
- ^ Korhonen, P .; Валлениус Дж. (1988). «Гонка Парето». Логистика военно-морских исследований. 35 (6): 615–623. Дои:10.1002 / 1520-6750 (198812) 35: 6 <615 :: AID-NAV3220350608> 3.0.CO; 2-K.
- ^ Чарнз, А. и Купер, W.W. (1961). Модели управления и промышленные приложения линейного программирования. Нью-Йорк: Вили.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ Заде, Л. (1965). «Нечеткие множества». Информация и контроль. 8 (3): 338–353. Дои:10.1016 / S0019-9958 (65) 90241-X.
- ^ Кини, Р. и Райффа, Х. (1976). Решения с множеством целей: предпочтения и компромиссы. Нью-Йорк: Вили.
- ^ Рой, Б. (1968). "La méthode ELECTRE". Revue d'Informatique et de Recherche Opérationelle (RIRO). 8: 57–75.
- ^ Шаффер, Дж. Д. (1984). Некоторые эксперименты в машинном обучении с использованием генетических алгоритмов с векторной оценкой, кандидатская диссертация. Нэшвилл: Университет Вандербильта.
- ^ Srinivas, N .; Деб, К. (1994). «Многокритериальная оптимизация с использованием недоминирующей сортировки в генетических алгоритмах». Эволюционные вычисления. 2 (3): 221–248. Дои:10.1162 / evco.1994.2.3.221. S2CID 13997318.
- ^ Deb, K .; Коксалан, М. (2010). "Специальный выпуск гостевой редакции о многоцелевых эволюционных алгоритмах, основанных на предпочтениях". IEEE Transactions по эволюционным вычислениям. 14 (5): 669–670. Дои:10.1109 / TEVC.2010.2070371.
- ^ Лю, Сифэн (2017). Анализ серых данных - методы, модели и приложения. Сингапур: Спрингер. С. 67–104. ISBN 978-981-10-1841-1.
- ^ Лю, Сифэн (2013). «О функциях измерения единообразного эффекта и взвешенной модели принятия решения с множеством атрибутов для серых целей». Журнал Серой Системы. Research Information Ltd. (Великобритания). 25 (1): 1–11. Дои:10.1007 / s40815-020-00827-8. S2CID 219090787.
- ^ Джавед, С. А. (2020). «Серый метод анализа абсолютного решения (GADA) для принятия решений по множеству критериев в условиях неопределенности». Международный журнал нечетких систем. Springer. 22 (4): 1073–1090. Дои:10.1007 / s40815-020-00827-8. S2CID 219090787.
- ^ Саати, Т. (1980). Процесс аналитической иерархии: планирование, установка приоритетов, распределение ресурсов. Нью-Йорк: Макгроу-Хилл.
- ^ Мардани, Аббас; Джусох, Ахмад; Завадскас, Эдмундас Казимерас (15 мая 2015 г.). «Методы и приложения для принятия решений с нечеткими множественными критериями - Обзор за два десятилетия с 1994 по 2014». Экспертные системы с приложениями. 42 (8): 4126–4148. Дои:10.1016 / j.eswa.2015.01.003.
- ^ Мардани, Аббас; Джусох, Ахмад; Нор, Халил MD; Халифа, Зайнаб; Закван, Норхаяти; Валипур, Алиреза (1 января 2015 г.). «Многокритериальные методы принятия решений и их приложения - обзор литературы с 2000 по 2014 гг.». Экономические исследования-Ekonomska Istraživanja. 28 (1): 516–571. Дои:10.1080 / 1331677X.2015.1075139. ISSN 1331-677X.
- ^ Мардани, Аббас; Джусох, Ахмад; Завадскас, Эдмундас Казимирас; Кавалларо, Фаусто; Халифа, Зайнаб (19 октября 2015 г.). «Устойчивая и возобновляемая энергия: обзор применения методов и подходов к принятию решений по множеству критериев». Устойчивость. 7 (10): 13947–13984. Дои:10.3390 / su71013947.
- ^ Мардани, Аббас; Завадскас, Эдмундас Казимирас; Говиндан, Каннан; Амат Сенин, Аслан; Джусо, Ахмад (4 января 2016 г.). "Техника ВИКОР: систематический обзор современной литературы по методологиям и приложениям". Устойчивость. 8 (1): 37. Дои:10.3390 / su8010037.
- ^ Мардани, Аббас; Завадскас, Эдмундас Казимирас; Халифа, Зайнаб; Джусох, Ахмад; Нор, Халил MD (2 июля 2016 г.). «Многокритериальные методы принятия решений в транспортных системах: систематический обзор новейшей литературы». Транспорт. 31 (3): 359–385. Дои:10.3846/16484142.2015.1121517. ISSN 1648-4142.
- ^ Мардани, Аббас; Джусох, Ахмад; Завадскас, Эдмундас Казимирас; Халифа, Зайнаб; Нор, Халил, доктор медицины (3 сентября 2015 г.). «Применение многокритериальных методов принятия решений и подходов к оценке качества услуг: систематический обзор литературы». Журнал экономики и менеджмента бизнеса. 16 (5): 1034–1068. Дои:10.3846/16111699.2015.1095233. ISSN 1611-1699.
- ^ Завадскас, Эдмундас Казимирас; Мардани, Аббас; Турскис, Зенонас; Джусох, Ахмад; Нор, Халил, доктор медицины (1 мая 2016 г.). «Разработка метода TOPSIS для решения сложных задач принятия решений - обзор событий с 2000 по 2015 год». Международный журнал информационных технологий и принятия решений. 15 (3): 645–682. Дои:10.1142 / S0219622016300019. ISSN 0219-6220.
- ^ Мардани, Аббас; Завадскас, Эдмундас Казимирас; Халифа, Зайнаб; Закуан, Норхаяти; Джусох, Ахмад; Nor, Khalil Md; Хошнуди, Масуме (1 мая 2017 г.). «Обзор многокритериальных приложений для принятия решений для решения задач энергоменеджмента: два десятилетия с 1995 по 2015». Обзоры возобновляемых и устойчивых источников энергии. 71: 216–256. Дои:10.1016 / j.rser.2016.12.053.
- ^ Заре, Моджтаба; Пал, Кристина; Рахнама, Хамед; Нилаши, Мехрбахш; Мардани, Аббас; Ибрагим, Осман; Ахмади, Хоссейн (1 августа 2016 г.). «Многокритериальный подход к принятию решений в электронном обучении: систематический обзор и классификация». Прикладные мягкие вычисления. 45: 108–128. Дои:10.1016 / j.asoc.2016.04.020.
- ^ Дидонис, Антанас. «Трансформации в бизнесе и экономике - Том 15, № 1 (37), 2016 - Статья». www.transformations.knf.vu.lt. В архиве с оригинала 29 августа 2017 г.. Получено 29 августа 2017.
- ^ Мардани, Аббас; Нилаши, Мехрбахш; Закуан, Норхаяти; Логанатан, Нантакумар; Сохейлирад, Сомайех; Саман, Мухамад Замери Мат; Ибрагим, Осман (1 августа 2017 г.). «Систематический обзор и мета-анализ методов SWARA и WASPAS: теория и приложения с последними нечеткими разработками». Прикладные мягкие вычисления. 57: 265–292. Дои:10.1016 / j.asoc.2017.03.045.
- ^ Хасели, Г., Шейх, Р., и Сана, С. С. (2019). Базис-критерий многокритериального метода принятия решений и его применения. Международный журнал менеджмента и инженерного менеджмента, 1-10. https://doi.org/10.1080/17509653.2019.1633964
- ^ Резаи, Джафар (2015). «Наихудший-лучший многокритериальный метод принятия решений». Омега. 53: 49–57. Дои:10.1016 / j.omega.2014.11.009.
- ^ Резаи, Джафар (2016). «Многокритериальный метод принятия решений наихудший-лучший: некоторые свойства и линейная модель». Омега. 64: 126–130. Дои:10.1016 / j.omega.2015.12.001.
- ^ Салабун, В. (2015). Метод характеристических объектов: новый дистанционный подход к многокритериальным задачам принятия решений. Журнал многокритериального анализа решений, 22 (1-2), 37-50.
- ^ Салабун, В., Пиегат, А. (2016). Сравнительный анализ методов MCDM для оценки смертности пациентов с острым коронарным синдромом. Обзор искусственного интеллекта. Первый онлайн: 3 сентября 2016 г.
- ^ Keshavarz Ghorabaee, M. et al. (2015) "Многокритериальная инвентаризационная классификация с использованием нового метода оценки на основе расстояния от среднего решения (EDAS) В архиве 2 сентября 2016 г. Wayback Machine ", Информатика, 26 (3), 435-451.
- ^ Эдвардс, В .; Барон, F.H. (1994). «Улучшенные простые методы измерения полезности по нескольким признакам». Организационное поведение и процессы принятия решений людьми. 60: 306–325. Дои:10.1006 / obhd.1994.1087.
- ^ Закери, С. (2018). Ранжирование на основе многокритериального метода принятия решений по оптимальным баллам. Системы Грея: теория и применение. doi:10.1108 / GS-09-2018-0040
- ^ Серафим, Оприкович; Gwo-Hshiung, Tzeng (2007). «Расширенный метод ВИКОР в сравнении с методами ранжирования». Европейский журнал операционных исследований. 178 (2): 514–529. Дои:10.1016 / j.ejor.2006.01.020.
- ^ Joglekar, Saurabh N .; Харкар, Рушикеш А .; Mandavgane, Sachin A .; Кулькарни, Бхаскар Д. (февраль 2018 г.). «Оценка устойчивости кирпичной кладки для недорогого жилья: сравнение кирпича на основе отходов и кирпича из обожженной глины». Устойчивые города и общество. 37: 396–406. Дои:10.1016 / j.scs.2017.11.025.
- ^ Аларкон, Вивиана; Агуадо, Антонио; Манга, Resmundo; Хоса, Алехандро (24 декабря 2010 г.). «Ценностная функция для оценки устойчивости: применение в промышленных зданиях». Устойчивость. 3 (1): 35–50. Дои:10.3390 / su3010035.
дальнейшее чтение
- Малиене, В. (2011). «Специализированная оценка имущества: анализ решений по множеству критериев». Журнал Retail & Leisure Property. 9 (5): 443–50. Дои:10.1057 / rlp.2011.7.
- Муллинер Э, Смоллбоун К., Малиене В. (2013). «Оценка доступности устойчивого жилья с использованием метода принятия решений по множеству критериев» (PDF). Омега. 41 (2): 270–79. Дои:10.1016 / j.omega.2012.05.002.
- Малиене, В .; и другие. (2002). «Применение нового метода многокритериального анализа при оценке имущества» (PDF). Международный Конгресс FIG XXII: 19–26.
- Краткая история, подготовленная Steuer and Zionts
- Малакути, Б. (2013). Операционные и производственные системы с множеством целей. Джон Вили и сыновья.


