Теорема Пика - Википедия - Picks theorem

я = 7

,

б = 8

,

А = я + .mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px;white-space:nowrap} б / 2 - 1 = 10

Треугольник с вершинами в нижнем левом, нижнем правом и верхнем правом точках имеет

я = 12

и

б = 14

, давая по теореме Пика

А = я + б / 2 - 1 = 18

; это подтверждается формулой площади треугольника 12 × основание × высота = 12 × 9 × 4 = 18.

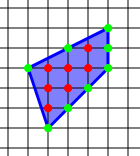
Учитывая простой многоугольник построенный на сетке равноудаленных точек (то есть точек с целое число координаты) так, чтобы все вершины точки сетки, Теорема Пика обеспечивает простой формула для расчета площадь $А$ этого многоугольника по количеству $я$ из решетки в интерьере расположен в многоугольнике и число $б$ из точки решетки на границе размещены по периметру многоугольника:^[1]

{ displaystyle A = i + { frac {b} {2}} - 1.}

В показанном примере у нас есть $я = 7$ внутренние точки и $б = 8$ граничные точки, поэтому площадь $А$ = 7 + 8/2 - 1 = 7 + 4 - 1 = 10 квадратных единиц.

Теорема, изложенная выше, верна только для просто многоугольники, то есть те, которые состоят из одной несамопересекающейся границы (и, следовательно, не содержат дыр). Для общего многоугольника формула Пика обобщается на^[2]^[3]

{ displaystyle A = v - { frac {1} {2}} e_ {b} + h-1}

куда ${ displaystyle v}$ - количество вершин как внутри, так и на границе многоугольника, ${ displaystyle e_ {b}}$ - количество ребер решетки на границе многоугольника, а ${ displaystyle h}$ - количество отверстий в многоугольнике.

В качестве примера рассмотрим «многоугольник», образованный соединением точек ${ Displaystyle (0,0), (2,0)}$ . Он имеет 3 вершины, 0 отверстий и 0 площадей. Чтобы формула работала, у нее должно быть 4 края. Таким образом, нужно просто пересчитать каждое ребро дважды, «по одному с каждой стороны».

Результат был впервые описан Георг Александр Пик в 1899 г.^[4] В Тетраэдр Рива показывает, что не существует аналога теоремы Пика в трех измерениях, который выражает объем многогранника путем подсчета его внутренних и граничных точек. Однако есть обобщение в более высоких измерениях через Полиномы Эрхарта.

Доказательство

Рассмотрим многоугольник $п$ и треугольник $Т$ , с одной кромкой, общей с $п$ . Предположим, что теорема Пика верна для обоих $п$ и $Т$ раздельно; мы хотим показать, что это верно и для многоугольника $PT$ полученный путем добавления $Т$ к $п$ . С $п$ и $Т$ разделяют ребро, все общие граничные точки вдоль ребра объединяются во внутренние точки, за исключением двух конечных точек края, которые объединяются с граничными точками. Итак, называя количество граничных точек общим $c$ , у нас есть^[5]

{ Displaystyle i_ {PT} = i_ {P} + i_ {T} + (c-2)}

и

{ displaystyle b_ {PT} = b_ {P} + b_ {T} -2 (c-2) -2.}

Из вышесказанного следует

{ Displaystyle i_ {P} + i_ {T} = i_ {PT} - (c-2)}

и

{ displaystyle b_ {P} + b_ {T} = b_ {PT} +2 (c-2) +2.}

Поскольку мы предполагаем теорему для $п$ и для $Т$ раздельно,

{ displaystyle { begin {align} A_ {PT} & = A_ {P} + A_ {T} & = left (i_ {P} + { frac {b_ {P}} {2}} - 1 right) + left (i_ {T} + { frac {b_ {T}} {2}} - 1 right) & = i_ {P} + i_ {T} + { frac {b_ {P} + b_ {T}} {2}} - 2 & = i_ {PT} - (c-2) + { frac {b_ {PT} +2 (c-2) +2} {2 }} - 2 & = i_ {PT} + { frac {b_ {PT}} {2}} - 1. end {align}}}

Следовательно, если теорема верна для многоугольников, построенных из $п$ треугольников, теорема верна и для многоугольников, построенных из $п + 1$ треугольники. Для общего многогранники, как известно, они всегда могут быть триангулированный. То, что это верно для измерения 2, - простой факт. Чтобы закончить доказательство математическая индукция, осталось показать, что теорема верна для треугольников. Проверка в этом случае может быть выполнена в следующие короткие шаги:

заметим, что формула верна для любого единичный квадрат (с вершинами, имеющими целочисленные координаты);
вывести из этого, что формула верна для любого прямоугольник с боков параллельно к топорам;
вывести его теперь для прямоугольных треугольников, полученных путем разрезания таких прямоугольников вдоль диагональ;
теперь любой треугольник можно превратить в прямоугольник, прикрепив такие прямоугольные треугольники; поскольку формула верна для прямоугольных треугольников и прямоугольника, она также следует для исходного треугольника.

Последний шаг использует тот факт, что если теорема верна для многоугольника $PT$ а для треугольника $Т$ , то это верно и для $п$ ; это можно увидеть с помощью расчета, очень похожего на показанный выше.

Неравенство для выпуклых множеств

Позволять ${ displaystyle C}$ - ограниченная выпуклая область в ${ Displaystyle mathbb {R} ^ {2}}$ , не обязательно закрытый. потом

{ displaystyle | L (C) | leq operatorname {Area} (C) + { frac {1} {2}} operatorname {Perimeter} (C) +1.}

^[2]

куда ${ Displaystyle L (C)}$ - множество точек решетки в ${ displaystyle C}$ , и ${ displaystyle | L (C) |}$ это их количество.

Доказательство проводится с помощью выпуклой оболочки ${ displaystyle { bar {C}}}$ из ${ Displaystyle L (C)}$ , который следует рассматривать как решеточную аппроксимацию ${ displaystyle C}$ , затем примените к нему теорему Пика.

{ displaystyle { begin {align} | L (C) | = | L ({ bar {C}}) | & = operatorname {Area} ({ bar {C}}) + { frac {1 } {2}} B ({ bar {C}}) + 1 & leq operatorname {Area} ({ bar {C}}) + { frac {1} {2}} operatorname { Периметр} ({ bar {C}}) + 1 & leq operatorname {Area} (C) + { frac {1} {2}} operatorname {Perimeter} (C) +1 end { выровнено}}}

куда ${ displaystyle B ({ bar {C}})}$ количество граничных точек ${ displaystyle { bar {C}}}$ , который равен количеству его ребер, и поскольку каждое ребро имеет длину не менее 1, ${ displaystyle B ({ bar {C}}) leq operatorname {Perimeter} ({ bar {C}})}$ . И шаг ${ displaystyle operatorname {Perimeter} ({ bar {C}}) leq operatorname {Perimeter} (C)}$ использует свойство, заключающееся в том, что между двумя вложенными выпуклыми замкнутыми кривыми внутренняя короче, что является применением Формула Крофтона.

Это все еще работает в вырожденном случае, когда ${ Displaystyle L (C)}$ находится на той же линии. Просто нужно пересчитать каждое ребро дважды, «по одному с каждой стороны».

Смотрите также

внешняя ссылка

[1] Трейнин, Дж. (Ноябрь 2007 г.). «Элементарное доказательство теоремы Пика». Математический вестник. 91 (522): 536–540. Дои:10.1017 / S0025557200182270.

[:0-2] а ^б Гарбетт, Дженнифер (18 ноября 2010 г.). "Геометрия точек решетки: теорема Пика и теорема Минковского, старшее упражнение по математике" (PDF). Архивировано из оригинал (PDF) 29 августа 2017 г.

[3] Беляев, Александр; Файоль, Пьер-Ален (8 августа 2019 г.). «Подсчет параллельных отрезков: новые варианты теоремы Пика о площадях». Математический интеллект. 41 (4): 1–7. Дои:10.1007 / s00283-019-09921-8. ISSN 0343-6993.

[4] Пик, Георг (1899). "Geometrisches zur Zahlenlehre". Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen "Lotos" в Праге. (Neue Folge). 19: 311–319. JFM 33.0216.01. CiteBank: 47270

[5] Бек, Матиас; Робинс, Синай (2007). Вычисление непрерывных дискретных чисел: целочисленное перечисление в многогранниках. Тексты для бакалавриата по математике. Нью-Йорк: Springer-Verlag. гл. 2. ISBN 978-0-387-29139-0. МИСТЕР 2271992.

[1]

[2]

[3]

[4]

[5]

Теорема Пика - Википедия - Picks theorem

Содержание

Доказательство

Неравенство для выпуклых множеств

Смотрите также

Рекомендации

внешняя ссылка