Замирание Рэлея - Rayleigh fading

Замирание Рэлея это статистический модель для эффекта распространение окружающая среда на радио сигнал, например, используемый беспроводной устройств.

В моделях рэлеевских замираний предполагается, что величина сигнала, прошедшего через такую среда передачи (также называемый канал связи ) будет меняться случайным образом, или тускнеть, по мнению Распределение Рэлея - радиальная составляющая суммы двух некоррелированных Гауссовский случайные переменные.

Рэлеевское замирание рассматривается как разумная модель для тропосферный и ионосферный распространение сигнала, а также эффект сильно застроенных городской среды по радиосигналам.^[1]^[2] Рэлеевские замирания наиболее применимы, когда нет преобладающего распространения по Поле зрения между передатчиком и приемником. Если есть доминирующая линия обзора, Rician увядание может быть более применимым. Рэлеевское замирание - это частный случай двухволновой с замиранием диффузной мощности (TWDP).

Модель

Рэлеевское замирание - разумная модель, когда в окружающей среде много объектов, которые разбросать радиосигнал до того, как он достигнет приемника. В Центральная предельная теорема считает, что при достаточно большом разбросе канал импульсивный ответ будет хорошо смоделирован как Гауссовский процесс независимо от распределения отдельных компонентов. Если в разбросе нет доминирующей компоненты, то такой процесс будет иметь нулевое значение. иметь в виду и фаза равномерно распределены между 0 и 2π радианы. В конверт отклика канала, следовательно, будет Распределенный Рэлея.

Вызов этой случайной переменной ${ displaystyle R}$ , у него будет функция плотности вероятности:^[1]

{ displaystyle p_ {R} (r) = { frac {2r} { Omega}} e ^ {- r ^ {2} / Omega}, r geq 0}

куда ${ displaystyle Omega = operatorname {E} (R ^ {2})}$ .

Часто элементы усиления и фазы искажения канала удобно представлять как комплексное число. В этом случае замирание Рэлея проявляется в предположении, что настоящий и воображаемый части ответа моделируются независимые и одинаково распределенные гауссовские процессы с нулевым средним, так что амплитуда отклика является суммой двух таких процессов.

Применимость

Было показано, что плотно застроенный Манхэттен приближается к рэлеевской среде.

Одна секунда рэлеевского замирания с максимальным доплеровским сдвигом 10 Гц.

Одна секунда рэлеевского замирания с максимальным доплеровским сдвигом 100 Гц.

Требование наличия большого количества рассеивателей означает, что рэлеевские замирания могут быть полезной моделью в сильно застроенных центрах городов, где есть нет прямой видимости между передатчиком и приемником и многими зданиями и другими объектами ослаблять, отражать, преломлять, и преломлять сигнал. Экспериментальная работа в Манхэттен нашел там затухание, близкое к рэлеевскому.^[3] В тропосферный и ионосферный распространение сигнала: многие частицы в атмосферных слоях действуют как рассеиватели, и такая среда также может приближаться к рэлеевскому замиранию. Если окружающая среда такова, что, помимо рассеяния, на приемнике наблюдается сильно доминирующий сигнал, обычно вызванный Поле зрения, то среднее значение случайного процесса больше не будет равняться нулю, а будет изменяться вокруг уровня мощности доминирующего пути. Такую ситуацию можно лучше смоделировать как Rician увядание.

Обратите внимание, что замирание Рэлея - это мелкомасштабный эффект. Будут присутствовать основные свойства среды, такие как потеря пути и слежка на который накладывается затухание.

Скорость затухания канала будет зависеть от скорости движения приемника и / или передатчика. Причины движения Доплеровский сдвиг в составляющих принятого сигнала. На рисунках показано изменение мощности постоянного сигнала в течение 1 секунды после прохождения через однолучевой канал с рэлеевскими замираниями с максимальным доплеровским сдвигом 10 Гц и 100 Гц. Эти доплеровские сдвиги соответствуют скоростям около 6 км / ч (4 мили в час) и 60 км / ч (40 миль в час) соответственно на частоте 1800 МГц, одной из рабочих частот для GSM мобильные телефоны. Это классическая форма рэлеевского выцветания. Обратите внимание, в частности, на «глубокие затухания», когда уровень сигнала может упасть в несколько тысяч раз, или в 30–40 раз. дБ.

Характеристики

Поскольку оно основано на хорошо изученном распределении с особыми свойствами, распределение Рэлея поддается анализу, и ключевые особенности, которые влияют на производительность беспроводной сети, имеют аналитические выражения.

Обратите внимание, что обсуждаемые здесь параметры предназначены для нестатического канала. Если канал не меняется со временем, он не исчезает, а вместо этого остается на определенном уровне. Отдельные экземпляры канала в этом случае не будут коррелированы друг с другом из-за предположения, что каждая из рассеянных составляющих затухает независимо. Как только относительное движение вводится между любым из передатчика, приемника и рассеивателя, замирание становится коррелированным и изменяется во времени.

Скорость переезда

Скорость пересечения уровня является мерой скорости замирания. Он определяет, как часто замирание пересекает некоторый порог, обычно в положительном направлении. Для рэлеевских замираний скорость пересечения уровней равна:^[4]

{ displaystyle mathrm {LCR} = { sqrt {2 pi}} f_ {d} rho e ^ {- rho ^ {2}}}

куда ${ displaystyle f_ {d}}$ - максимальный доплеровский сдвиг и ${ Displaystyle , ! rho}$ - пороговый уровень, нормированный на среднеквадратическое значение (RMS) уровень сигнала:

{ displaystyle rho = { frac {R _ { mathrm {threshold}}} {R _ { mathrm {rms}}}}.}

Средняя продолжительность затухания

Средняя длительность замирания количественно определяет, как долго сигнал находится ниже порогового значения. ${ Displaystyle , ! rho}$ . Для рэлеевского замирания средняя продолжительность замирания составляет:^[4]

{ displaystyle mathrm {AFD} = { frac {e ^ { rho ^ {2}} - 1} { rho f_ {d} { sqrt {2 pi}}}}.}.

Скорость перехода уровня и средняя длительность замирания, взятые вместе, дают полезные средства для характеристики серьезности замирания во времени.

Для конкретного нормализованного порогового значения ${ displaystyle rho}$ , произведение средней продолжительности замирания и скорости пересечения уровней является постоянным и определяется выражением

{ displaystyle mathrm {AFD} times mathrm {LCR} = 1-e ^ {- rho ^ {2}}.}

Доплеровская спектральная плотность мощности

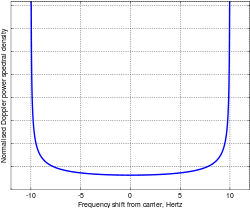
Нормированный доплеровский спектр мощности рэлеевских замираний с максимальным доплеровским сдвигом 10 Гц.

Доплер спектральная плотность мощности канала с замиранием описывает, насколько сильно он вызывает спектральное расширение. Это показывает, как чистая частота, например, чистая синусоида, которая является импульс в частотной области распространяется по частоте при прохождении через канал. Это преобразование Фурье функции автокорреляции времени. Было показано, что для рэлеевского замирания с вертикальной приемной антенной с одинаковой чувствительностью во всех направлениях:^[5]

{ displaystyle S ( nu) = { frac {1} { pi f_ {d} { sqrt {1- left ({ frac { nu} {f_ {d}}} right) ^ { 2}}}}},}

куда ${ Displaystyle , ! ню}$ - сдвиг частоты относительно несущей частоты. Это уравнение справедливо только для значений ${ Displaystyle , ! ню}$ между ${ displaystyle pm f_ {d}}$ ; вне этого диапазона спектр равен нулю. Этот спектр показан на рисунке для максимального доплеровского сдвига 10 Гц. «Форма чаши» или «форма ванны» - классическая форма этого доплеровского спектра.

Создание рэлеевского замирания

Как описано над канал с рэлеевскими замираниями может быть смоделирован путем генерации действительной и мнимой частей комплексного числа в соответствии с независимыми нормальными гауссовыми переменными. Однако иногда бывает так, что интерес представляют просто колебания амплитуды (например, на рисунке, показанном выше). Есть два основных подхода к этому. В обоих случаях цель состоит в том, чтобы произвести сигнал, который имеет доплеровский спектр мощности, указанный выше, и эквивалентные свойства автокорреляции.

Модель Джейкса

В своей книге^[6] Джейкс популяризировал модель замирания Рэлея, основанную на суммировании. синусоиды. Пусть рассеиватели равномерно распределены по окружности под углами ${ Displaystyle альфа _ {п}}$ с ${ displaystyle k}$ лучи, исходящие от каждого рассеивателя. Доплеровский сдвиг на луче ${ displaystyle n}$ является

{ Displaystyle , ! е_ {п} = е_ {d} соз альфа _ {п}}

и с ${ displaystyle M}$ таких рассеивателей, рэлеевское затухание ${ Displaystyle к ^ { текст {th}}}$ форма волны с течением времени ${ displaystyle t}$ можно смоделировать как:

{ displaystyle { begin {align} R (t, k) = 2 { sqrt {2}} left [ sum _ {n = 1} ^ {M} right. & left ( cos beta _ {n} + j sin beta _ {n} right) cos left (2 pi f_ {n} t + theta _ {n, k} right) [4pt] & left. {} + { frac {1} { sqrt {2}}} left ( cos alpha + j sin alpha right) cos (2 pi f_ {d} t) right]. конец {выровнен}}}

Здесь, ${ Displaystyle , ! альфа}$ и ${ displaystyle , ! beta _ {п}}$ и ${ Displaystyle , ! theta _ {п, к}}$ параметры модели с ${ Displaystyle , ! альфа}$ обычно устанавливается на ноль, ${ displaystyle , ! beta _ {п}}$ выбран так, чтобы не было взаимной корреляции между действительной и мнимой частями ${ Displaystyle R (т)}$ :

{ displaystyle , ! beta _ {n} = { frac { pi n} {M + 1}}}

и ${ Displaystyle , ! theta _ {п, к}}$ используется для генерации нескольких сигналов. Если моделируется однолучевой канал, так что есть только одна форма волны, тогда ${ Displaystyle , ! theta _ {п}}$ может быть нулевым. Если многолучевой, частотно-избирательный канал моделируется таким образом, что требуется несколько форм сигналов, Джейкс предполагает, что некоррелированные формы сигналов задаются выражением

{ displaystyle theta _ {n, k} = beta _ {n} + { frac {2 pi (k-1)} {M + 1}}.}

Фактически, было показано, что формы сигналов коррелированы между собой - они имеют ненулевую взаимную корреляцию - за исключением особых обстоятельств.^[7] Модель также детерминированный (он не имеет случайного элемента после выбора параметров). Модифицированная модель Джейкса^[8] выбирает немного другие интервалы для рассеивателей и масштабирует их формы волны, используя Последовательности Уолша-Адамара для обеспечения нулевой взаимной корреляции. Параметр

{ displaystyle alpha _ {n} = { frac { pi (n-0,5)} {2M}} { text {and}} beta _ {n} = { frac { pi n} {M }},}

приводит к следующей модели, обычно называемой моделью Дента или модифицированной моделью Джейкса:

{ Displaystyle R (t, k) = { sqrt { frac {2} {M}}} sum _ {n = 1} ^ {M} A_ {k} (n) left ( cos beta _ {n} + j sin beta _ {n} right) cos left (2 pi f_ {d} t cos alpha _ {n} + theta _ {n} right).}

Весовые функции ${ Displaystyle A_ {k} (п)}$ являются ${ displaystyle k}$ ^th Последовательность Уолша – Адамара в ${ displaystyle n}$ . Поскольку они имеют нулевую взаимную корреляцию по конструкции, эта модель приводит к некоррелированным сигналам. Фазы ${ Displaystyle , ! theta _ {п}}$ могут быть инициализированы случайным образом и не влияют на свойства корреляции. В быстрое преобразование Уолша можно использовать для эффективного создания образцов с использованием этой модели.

Модель Джейкса также способствовала популяризации доплеровского спектра, связанного с рэлеевским замиранием, и, как результат, этот доплеровский спектр часто называют спектром Джейкса.

Фильтрованный белый шум

Другой способ сгенерировать сигнал с требуемым доплеровским спектром мощности - пройти через белый Гауссовский шум сигнал через фильтр Гаусса с частотной характеристикой, равной квадратному корню из требуемого доплеровского спектра. Хотя он проще, чем модели, приведенные выше, и недетерминирован, он представляет некоторые вопросы реализации, связанные с необходимостью фильтров высокого порядка для аппроксимации иррациональной функции квадратного корня в отклике и выборки гауссовой формы волны с соответствующей частотой.