Лобе Роша - Roche lobe
эта статья нужны дополнительные цитаты для проверка. (Май 2008 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В Лобе Роша это регион вокруг звезда в бинарная система в пределах которого вращающийся по орбите материал гравитационно привязан к этой звезде. Это область приблизительно каплевидной формы, ограниченная критическим гравитационный эквипотенциальный, причем вершина слезы направлена в сторону другой звезды (вершина находится на L1 Точка лагранжиана системы).
Доля Роша отличается от Сфера Роша, что аппроксимирует гравитационную сфера влияния одного астрономическое тело перед лицом возмущения от более массивного тела, вокруг которого он вращается. Он отличается от Предел Роша, которое представляет собой расстояние, на котором объект, удерживаемый только гравитацией, начинает разрушаться из-за приливные силы. Полость Роша, предел Роша и сфера Роша названы в честь Французский астроном Эдуард Рош.
Определение

В бинарной системе с круговой орбитой часто бывает полезно описать систему в системе координат, которая вращается вместе с объектами. В этом неинерциальная система отсчета, нужно учитывать центробежная сила в дополнение к гравитации. Их вместе можно описать как потенциал, так что, например, звездные поверхности лежат вдоль эквипотенциальных поверхностей.
Рядом с каждой звездой поверхности равны гравитационный потенциал приблизительно сферический и концентричен с более близкой звездой. Вдали от звездной системы эквипотенциалы примерно равны эллипсоидальный и вытянуты параллельно оси, соединяющей центры звезд. Критический эквипотенциал пересекает себя в L1 Точка лагранжиана системы, образуя двухлепестковую восьмерку с одной из двух звезд в центре каждой доли. Этот критический эквипотенциал определяет доли Роша.[2]
Где материя движется относительно вращающейся в одном направлении рамы будет казаться, что на него действует Сила Кориолиса. Это не выводится из модели лепестков Роша, поскольку сила Кориолиса не являетсяконсервативная сила (т.е. не может быть представлен скалярным потенциалом).
Дальнейший анализ
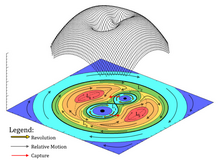
На графике гравитационного потенциала L1, L2, L3, L4, L5 находятся в синхронном вращении с системой. Области красного, оранжевого, желтого, зеленого, голубого и синего цветов - это потенциальные массивы от высокого к низкому. Красные стрелки обозначают вращение системы, а черные стрелки - относительные перемещения обломков.
Мусор движется быстрее в области с более низким потенциалом и медленнее в области с высоким потенциалом. Таким образом, относительное движение обломков на нижней орбите совпадает с направлением вращения системы, а на верхней орбите противоположно.
L1 - точка равновесия гравитационного захвата. Это граница гравитации двойной звездной системы. Это минимальное потенциальное равновесие среди L1, L2, L3, L4 и я5. Это самый простой способ перемещения мусора между Сфера холма (внутренний круг синего и голубого цветов) и общие области гравитации (восьмерки желтого и зеленого цветов на внутренней стороне).

L2 и я3 являются точками равновесия гравитационных возмущений. Пройдя через эти две точки равновесия, обломки могут перемещаться между внешней областью (желтые и зеленые восьмерки на внешней стороне) и областью общей гравитации двойной системы.
L4 и я5 - это максимальные потенциальные точки в системе. Это неустойчивые равновесия. Если соотношение масс двух звезд станет больше, то оранжевый, желтый и зеленый области станут подкова орбита.
Красная область станет орбита головастика.
Массообмен
Когда звезда «выходит за пределы своей полости Роша», ее поверхность выходит за пределы своей полости Роша, и материал, который находится за пределами полости Роша, может «упасть» в полость Роша другого объекта через первую точку Лагранжа. В бинарной эволюции это называется массообмен через Рош-лепестковое переполнение.
В принципе, массоперенос может привести к полному разрушению объекта, поскольку уменьшение массы объекта приводит к уменьшению его доли Роша. Однако в целом этого не происходит по нескольким причинам. Во-первых, уменьшение массы звезды-донора может вызвать сокращение и звезды-донора, что, возможно, предотвратит такой исход. Во-вторых, с передачей массы между двумя компонентами двойной системы угловой момент В то время как перенос массы от более массивного донора к менее массивному аккретору обычно приводит к сокращению орбиты, обратное вызывает расширение орбиты (в предположении сохранения массы и углового момента). Расширение двойной орбиты приведет к менее резкому сжатию или даже расширению доли Роша донора, часто предотвращая разрушение донора.
Чтобы определить стабильность массопереноса и, следовательно, точную судьбу звезды-донора, необходимо принять во внимание, как радиус звезды-донора и радиус ее полости Роша реагируют на потерю массы от донора; если звезда расширяется быстрее, чем ее полость Роша, или сжимается медленнее, чем ее полость Роша в течение длительного времени, массоперенос будет нестабильным, и звезда-донор может распасться. Если звезда-донор расширяется медленнее или сжимается быстрее, чем ее полость Роша, массоперенос, как правило, будет стабильным и может продолжаться в течение длительного времени.
Массоперенос из-за переполнения лепестка Роша является причиной ряда астрономических явлений, в том числе Системы Алгола, повторяющиеся новые (двойные звезды состоящий из красный гигант и белый Гном которые находятся достаточно близко, чтобы материал красного гиганта стекал на белый карлик), Рентгеновские двойные системы и миллисекундные пульсары. Такой массоперенос за счет переполнения полости Роша (RLOF) далее разбивается на три различных случая:
Случай А
Случай A RLOF возникает, когда звезда-донор сжигание водорода. Согласно Нельсону и Эгглтону, существует ряд подклассов.[3] которые воспроизводятся здесь:
ОБЪЯВЛЕНИЕ динамичный:
когда RLOF случается со звездой с глубоким зона конвекции. Массовый перенос происходит быстро на динамическая шкала времени звезды и может закончиться полным слияние.
AR быстрый контакт:
похоже на AD, но по мере того, как звезда, на которую быстро аккрецирует вещество, набирает массу, она приобретает достаточно физических размеров, чтобы достичь своей собственной полости Роша. В таких случаях система проявляется как контакт двоичный например, W переменная Ursae Majoris.
В КАЧЕСТВЕ медленный контакт:
похоже на AR, но происходит только короткий период быстрого массопереноса, за которым следует гораздо более длительный период медленного массопереноса. В конце концов звезды войдут в контакт, но к тому моменту, когда это произойдет, они существенно изменились. Переменные Алгола являются результатом таких ситуаций.
AE ранний обгон:
похожа на AS, но звезда, набирающая массу, обгоняет звезду, жертвующую массу, чтобы пройти мимо главной последовательности. Звезда-донор может уменьшиться настолько, что прекратит массоперенос, но в конечном итоге массоперенос начнется снова, поскольку звездная эволюция продолжается, что приводит к случаям
AL поздний обгон:
случай, когда звезда, которая изначально была донором, подвергается сверхновая звезда после того, как другая звезда прошла собственный раунд RLOF.
AB двоичный:
случай, когда звезды переключаются туда и обратно, один из которых проходит RLOF не менее трех раз (технически подкласс вышеупомянутого).
AN Обгон запрещен:
случай, когда звезда, которая изначально была донором, переживает сверхновую, прежде чем другая звезда достигнет фазы RLOF.
AG гигант:
Массоперенос не начинается, пока звезда не достигнет Красный гигант филиал но прежде, чем он исчерпает свое водородное ядро (после чего система описывается как Случай B).
Случай B
Случай B происходит, когда RLOF запускается, в то время как донором является звезда, горящая постоядровым водородом / горящей водородной оболочкой. Этот случай можно разделить на классы Br и Bc.[4] в зависимости от того, происходит ли перенос массы от звезды, в которой доминирует зона излучения (Br) и, следовательно, развивается как ситуация с большей частью случая A RLOF или конвективной зоны (Bc), после которой a общий конверт может произойти фаза (аналогично случаю C).[5] Альтернативное разделение случаев - это Ba, Bb и Bc, которые примерно соответствуют RLOF-фазам, которые происходят во время синтеза гелия, после синтеза с гелием, но до слияния углерода или после слияния углерода в высокоразвитой звезде.[6]
Случай C
Случай C происходит, когда RLOF запускается, когда донор находится в фазе горения гелиевой оболочки или превышает ее. Эти системы встречаются редко, но это может быть связано с критерий отбора.[7]
Геометрия
Точная форма полости Роша зависит от соотношения масс. , и должны оцениваться численно. Однако для многих целей полезно аппроксимировать полость Роша сферой того же объема. Приблизительная формула для радиуса этой сферы:
где и .Функция больше, чем за . Длина А орбитальное разделение системы и р1 - радиус сферы, объем которой приближается к полости Роша с массой M1. Эта формула имеет точность около 2%.[2] Другая приблизительная формула была предложена Эгглтоном и гласит:
Эта формула дает результаты с точностью до 1% во всем диапазоне отношения масс. .[8]
Рекомендации
- ^ Источник
- ^ а б Пачинский, Б. (1971). «Эволюционные процессы в тесных двоичных системах». Ежегодный обзор астрономии и астрофизики. 9: 183–208. Bibcode:1971ARA&A ... 9..183P. Дои:10.1146 / annurev.aa.09.090171.001151.
- ^ Nelson, C.A .; Эгглтон, П. П. (2001). «Полный обзор случая двоичной эволюции в сравнении с наблюдаемыми системами типа Алгола». Астрофизический журнал. 552 (2): 664–678. arXiv:astro-ph / 0009258. Bibcode:2001ApJ ... 552..664N. Дои:10.1086/320560. S2CID 119505485.
- ^ Vanbeveren, D .; Меннекенс, Н. (2014-04-01). «Слияние массивных двойных компактных объектов: источники гравитационных волн и производственные площадки r-технологических элементов». Астрономия и астрофизика. 564: A134. arXiv:1307.0959. Bibcode:2014A&A ... 564A.134M. Дои:10.1051/0004-6361/201322198. ISSN 0004-6361.
- ^ Vanbeveren, D .; Ренсберген, В. ван; Лур, К. де (2001-11-30). Самые яркие двоичные файлы. Springer Science & Business Media. ISBN 9781402003769.
- ^ Бхаттачарья, D; ван ден Хеувель, Э. П. Дж (1991-05-01). «Формирование и эволюция двойных и миллисекундных радиопульсаров». Отчеты по физике. 203 (1): 1–124. Bibcode:1991ФР ... 203 .... 1Б. Дои:10.1016 / 0370-1573 (91) 90064-С. ISSN 0370-1573.
- ^ Подсядловский, Филипп (февраль 2014 г.). «Эволюция двойных систем». Аккреционные процессы в астрофизике. Получено 2019-08-12.
- ^ Эгглтон, П. П. (1 мая 1983 г.). «Аппроксимации радиусов лепестков Роша». Астрофизический журнал. 268: 368. Bibcode:1983ApJ ... 268..368E. Дои:10.1086/160960.
Источники
- Моррис, С. (Февраль 1994 г.). «Два математических разложения эквипотенциалов Роша». Публикации Тихоокеанского астрономического общества. 106 (696): 154–155. Bibcode:1994ПАСП..106..154М. Дои:10.1086/133361. JSTOR 40680260.
- Моррис, С. (1 августа 1999 г.). "Пределы наклонения парных затмений двойных звезд". Астрофизический журнал. 520 (2): 797–804. Bibcode:1999ApJ ... 520..797M. Дои:10.1086/307488.


![{ displaystyle { frac {r_ {1}} {A}} = max {[f_ {1}, f_ {2}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65a796ffb605ad9afa0d1088583ce6a77f2b414c)







