Звездная пульсация - Stellar pulsation
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|

Звездные пульсации вызваны расширением и сжатием внешних слоев, поскольку звезда стремится поддерживать равновесие. Эти колебания звездный радиус вызвать соответствующие изменения в светимость звезды. Астрономы могут установить этот механизм, измерив спектр и соблюдая Эффект Допплера.[1] Многие внутренние переменные звезды которые пульсируют с большими амплитуды, например, классический Цефеиды, RR Lyrae звезды и большой амплитуды Дельта Скути звезды показывают регулярно кривые блеска.
Это регулярное поведение контрастирует с изменчивостью звезд, которые лежат параллельно стороне высокой светимости / низкой температуры классических переменных звезд в Диаграмма Герцшпрунга – Рассела. Наблюдается, что эти гигантские звезды испытывают пульсации в диапазоне от слабой неоднородности, когда еще можно определить среднее время цикла или период, (как и в большинстве Жилой дом Таури и полурегулярные переменные ) к практически отсутствию повторяемости в нерегулярный переменные. В Переменные W Virginis находятся на интерфейсе; короткопериодные - регулярные, а более длиннопериодные показывают первые относительно регулярные изменения в циклах пульсаций, за которыми следует начало легкой нерегулярности, как в звездах RV Тельца, в которые они постепенно превращаются по мере увеличения их периодов.[2][3] Теории звездной эволюции и пульсации предполагают, что эти неправильные звезды имеют гораздо более высокое отношение светимости к массе (L / M).
Многие звезды представляют собой нерадиальные пульсаторы, у которых флуктуации яркости меньше, чем у обычных переменных, используемых в качестве стандартных свечей.[4][5]
Регулярные переменные
Предпосылкой для нерегулярной переменности является то, что звезда может изменять свою амплитуду в масштабе времени периода. Другими словами, связь между пульсацией и тепловым потоком должна быть достаточно большой, чтобы допускать такие изменения. Эта связь измеряется относительной линейной скоростью роста или убывания κ (каппа ) амплитуды заданного нормальный режим за один цикл пульсации (период). Для регулярных переменных (цефеиды, RR Lyrae и др.) Численное моделирование звезд и линейное моделирование анализ устойчивости показывают, что κ составляет не более пары процентов для соответствующих возбужденных режимов пульсации. С другой стороны, такой же анализ показывает, что для моделей с высоким L / M κ значительно больше (30% или выше).
Для обычных переменных небольшие относительные темпы роста κ означают, что существуют две различные шкалы времени, а именно период колебаний и более длительное время, связанное с изменением амплитуды. Математически говоря, динамика имеет центральный коллектор, или, точнее, ближний центральный коллектор. Кроме того, было обнаружено, что звездные пульсации имеют лишь слабую нелинейность в том смысле, что их описание может быть ограниченными степенями амплитуд пульсаций. Эти два свойства очень общие и встречаются для колебательные системы во многих других областях, таких как динамика населения, океанография, физика плазмы, так далее.
Слабая нелинейность и большой временной масштаб изменения амплитуды позволяет упростить временное описание пульсирующей системы до описания только амплитуд пульсаций, тем самым устраняя движение в коротком временном масштабе периода. Результатом является описание системы в терминах амплитудных уравнений, усеченных до малых степеней амплитуд. Такие уравнения амплитуд были получены с помощью различных методов, например то Метод Пуанкаре – Линдштедта исключения вековых членов, или метод многократных асимптотических возмущений,[6][7][8] и в более общем плане теория нормальной формы.[9][10][11]
Например, в случае двух нерезонансных мод ситуация, обычно встречающаяся в переменных RR Lyrae, временная эволюция амплитуд A1 и А2 из двух нормальные режимы 1 и 2 управляется следующим набором обыкновенные дифференциальные уравнения
где Qij - коэффициенты нерезонансной связи.[12][13]
Эти уравнения амплитуды ограничены нетривиальными нелинейностями низшего порядка. Решения, представляющие интерес в теории звездных пульсаций, представляют собой асимптотические решения (поскольку время стремится к бесконечности), потому что временной масштаб для вариаций амплитуды обычно очень мал по сравнению с временным масштабом эволюции звезды, который является шкала времени ядерного горения. Приведенные выше уравнения имеют фиксированная точка решения с постоянными амплитудами, соответствующие одномодовым (A1 0, А2 = 0) или (A1 = 0, А2 0) и двухрежимный (A1 0, А20) решения. Они соответствуют однократным и двоякопериодическим пульсациям звезды. Важно подчеркнуть, что никакого другого асимптотического решения вышеупомянутых уравнений для физических (т. Е. Отрицательных) коэффициентов связи не существует.
За резонансный моды соответствующие уравнения амплитуды содержат дополнительные члены, которые описывают резонансную связь между модами. Прогрессия Герцшпрунга в морфологии кривых блеска классических (однопериодических) цефеид является результатом хорошо известного резонанса 2: 1 между основной модой пульсации и второй модой. обертон режим.[14] Уравнение амплитуды может быть расширено на нерадиальные звездные пульсации.[15][16]
В общем анализе пульсирующих звезд уравнения амплитуды допускают бифуркационная диаграмма между возможными пульсационными состояниями, которые необходимо отобразить. На этом снимке границы полоса нестабильности где в процессе эволюции звезды возникает пульсация, соответствующая Бифуркация хопфа.[17]
Наличие центрального многообразия исключает возможность хаотических (т.е. нерегулярных) пульсаций на временной шкале периода. Хотя уравнения резонансной амплитуды достаточно сложны, чтобы допускать хаотические решения, это совершенно другой хаос, потому что он заключается во временном изменении амплитуд и происходит в длительном масштабе времени.
Хотя долговременное нерегулярное поведение временных вариаций амплитуд пульсаций возможно, когда применяются уравнения амплитуд, это не общая ситуация. Действительно, для большинства наблюдений и моделирования пульсации этих звезд происходят с постоянными амплитудами Фурье, что приводит к регулярным пульсациям, которые могут быть периодическими или многопериодическими (квазипериодическими в математической литературе).
Нерегулярные пульсации
В кривые блеска присущих переменные звезды с большими амплитудами на протяжении веков, как известно, демонстрируют поведение, идущее от крайней регулярности, как для классических Цефеиды и RR Lyrae звезд, до крайней неправильности, как для так называемых Неправильные переменные. в Население II звезды эта неравномерность постепенно увеличивается с низкого периода Переменные W Virginis сквозь Жилой дом Таури переменных в режим полуправильные переменные. Низкоразмерный хаос в звездных пульсациях - это современная интерпретация этого установленного явления.
Регулярное поведение цефеид
Регулярное поведение цефеид успешно моделируется с помощью численной гидродинамики с 1960-х годов.[18][19] и с теоретической точки зрения это легко понять как следствие наличия центральный коллектор которое возникает из-за слабодиссипативного характера динамическая система.[20] Это, а также слабая нелинейность пульсаций позволяют описать систему в терминах амплитудных уравнений[21][22] и построение бифуркационной диаграммы (см. также теория бифуркации ) возможных видов пульсации (или предельные циклы ), такой основной режим пульсация, первая или вторая обертон пульсация, или более сложные двухмодовые пульсации, при которых несколько мод возбуждаются с постоянной амплитудой. Границы полоса нестабильности где в процессе эволюции звезды возникает пульсация, соответствующая Бифуркация хопфа.
Неравномерность звезд Population II
Напротив, неоднородность звезд населения II с большой амплитудой объяснить сложнее. Изменение амплитуды пульсации за один период предполагает большой диссипации, и, следовательно, не существует центрального многообразия. Были предложены различные механизмы, но их не хватает. Один предполагает наличие нескольких близко расположенных частот пульсаций, которые будут биться друг против друга, но таких частот не существует в соответствующих звездных моделях. Другое, более интересное предположение состоит в том, что вариации имеют стохастический характер,[23] но не было предложено или не существует механизма, который мог бы обеспечить энергию для таких больших наблюдаемых изменений амплитуды. В настоящее время установлено, что механизм, лежащий в основе нерегулярных кривых блеска, лежит в основе низкоразмерной хаотической динамики (см. Также Теория хаоса ). Этот вывод основан на двух типах исследований.
CFD моделирования
В вычислительная гидродинамика численные прогнозы пульсаций последовательности звездных моделей W Virginis демонстрируют два подхода к нерегулярному поведению, которые являются явным признаком низкоразмерных хаос. Первое указание исходит от карты первого возвращения в котором один изображает один максимальный радиус или любую другую подходящую переменную в сравнении со следующим. Последовательность моделей показывает бифуркация удвоения периода, или каскад, ведущий к хаосу. Почти квадратичная форма карты указывает на хаос и подразумевает лежащую в основе карта подковы.[24][25] Другие последовательности моделей следуют несколько иным путем, но тоже к хаосу, а именно Путь Поммо – Манневиля или касательная бифуркация маршрут.[26][27]
Ниже показана аналогичная визуализация каскада удвоения периода к хаосу для последовательности звездных моделей, различающихся средней температурой их поверхности T. На графике показаны тройки значений радиуса звезды (Rя, Ря + 1, Ря + 2) где индексы я, я + 1, я + 2 указывают последовательные временные интервалы.
 | 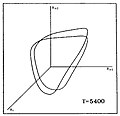 |  | 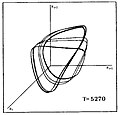 | 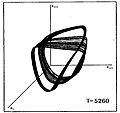 |  |
| P0 | P2 | P4 | P8 | Полосатый хаос | FullChaos |
Присутствие низкоразмерного хаоса подтверждается также другим, более сложным анализом модельных пульсаций, который выделяет самые низкие неустойчивые периодические орбиты и исследует их топологическую организацию (скручивание). Лежащий в основе аттрактор оказывается окаймленным как Аттрактор Ресслера, однако с дополнительным поворотом ремешка.[28]
Реконструкция глобального потока по наблюдаемым кривым блеска
Методика реконструкция глобального потока[29] использует один наблюдаемый сигнал {sя}, чтобы вывести свойства динамической системы, которая его сгенерировала. Первые N-мерные "векторы" Sя= (sя, ся-1, сi-2, ..., сi-N + 1). Следующий шаг - найти выражение для нелинейной оператор эволюции M который берет систему от времени i до момента i + 1, т.е.Sя + 1= M (Sя).Теорема Такенса гарантирует, что в очень общих обстоятельствах топологические свойства этого восстановленного оператора эволюции такие же, как у физической системы, при условии, что размер встраивания N достаточно велико. от знания одной наблюдаемой переменной можно сделать вывод о свойствах реальной физической системы, которая управляется рядом независимых переменных.
Этот подход был применен к AAVSO данные для звезды R Scuti[30][31]Можно сделать вывод, что нерегулярные пульсации этой звезды возникают из лежащей в основе четырехмерной динамики. Другими словами, это говорит о том, что из любых 4-х соседних наблюдений можно предсказать следующее. С физической точки зрения это говорит о том, что есть 4 независимых переменных, которые описывают динамику системы. Методика ложные ближайшие соседи подтверждает размерность вложения 4. фрактальная размерность динамики R Scuti, как выводится из вычисленных Показатели Ляпунова находится между 3,1 и 3,2.

Из анализа фиксированные точки оператора эволюции можно вывести красивую физическую картину, а именно, что пульсации возникают из-за возбуждения нестабильной моды пульсаций, которая нелинейно соединяется со второй устойчивой модой пульсаций, которая находится в соотношении 2: 1 резонанс с первым, сценарий, описываемый теоремой Шильникова.[32]
Этот резонансный механизм не ограничивается R Scuti, но, как было обнаружено, справедлив для нескольких других звезд, для которых данные наблюдений достаточно хороши.[33]
Рекомендации
- ^ Купелис, Тео (2010). В поисках Вселенной. Джонс и Бартлетт в области физических наук (6-е изд.). Джонс и Бартлетт Обучение. ISBN 978-0-7637-6858-4.
- ^ Alcock, C .; Allsman, R.A .; Alves, D. R .; Axelrod, T. S .; Беккер, А .; Bennett, D.P .; Cook, K. H .; Freeman, K. C .; Griest, K .; Lawson, W. A .; Ленер, М. Дж .; Marshall, S.L .; Миннити, Д .; Peterson, B.A .; Поллард, Карен Р .; Pratt, M. R .; Куинн, П. Дж .; Роджерс, А. У .; Sutherland, W .; Томаней, А .; Велч, Д. Л. (1998). "Переменный список звезд LMC проекта MACHO. VII. Открытие звезд RV Тельца и новых цефеид типа II в Большом Магеллановом облаке". Астрономический журнал. 115 (5): 1921. Bibcode:1998AJ .... 115.1921A. Дои:10.1086/300317.
- ^ Soszyński, I .; Удальский, А .; Шиманский, М. К .; Кубяк, М .; Pietrzyński, G .; Wyrzykowski, Ł .; Szewczyk, O .; Ulaczyk, K .; Полески, Р. (2008). "Эксперимент по оптическому гравитационному линзированию. Каталог переменных звезд OGLE-III. Цефеиды II типа и аномальные цефеиды в Большом Магеллановом облаке". Acta Astronomica. 58: 293. Bibcode:2008AcA .... 58..293S.
- ^ Grigahcène, A .; Antoci, V .; Balona, L .; Catanzaro, G .; Daszyńska-Daszkiewicz, J .; Guzik, J. A .; Handler, G .; Houdek, G .; Курц, Д. В .; Маркони, М .; Монтейро, М. Дж. П. Ф. Г .; Моя, А .; Ripepi, V .; Suárez, J. -C .; Uytterhoeven, K .; Borucki, W. J .; Браун, Т. М .; Christensen-Dalsgaard, J .; Gilliland, R.L .; Jenkins, J.M .; Kjeldsen, H .; Koch, D .; Bernabei, S .; Bradley, P .; Breger, M .; Di Criscienzo, M .; Dupret, M. -A .; García, R.A .; Гарсиа Эрнандес, А .; и другие. (2010). "Гибридные γ Doradus-δ Щитовидные пульсаторы: новый взгляд на физику колебаний на основе наблюдений Кеплера". Астрофизический журнал. 713 (2): L192. Bibcode:2010ApJ ... 713L.192G. Дои:10.1088 / 2041-8205 / 713/2 / L192.
- ^ Mosser, B .; Belkacem, K .; Goupil, M. -J .; Miglio, A .; Morel, T .; Barban, C .; Бауден, Ф .; Hekker, S .; Samadi, R .; Де Риддер, Дж .; Weiss, W .; Auvergne, M .; Баглин, А. (2010). «Сейсмические свойства красных гигантов проанализированы с помощью CoRoT». Астрономия и астрофизика. 517: A22. arXiv:1004.0449. Bibcode:2010A & A ... 517A..22M. Дои:10.1051/0004-6361/201014036.
- ^ Джимбовский, В. (1980). «Переменные Delta Scuti - связующее звено между пульсаторами гигантского и карликового типов». Нерадиальные и нелинейные пульсации звезд.. 125: 22. Bibcode:1980ЛНП ... 125 ... 22Д. Дои:10.1007/3-540-09994-8_2.
- ^ Buchler, J. R .; Гупиль, М. -Дж. (1984). «Амплитудные уравнения для неадиабатических нелинейных звездных пульсаторов. I - формализм». Астрофизический журнал. 279: 394. Bibcode:1984ApJ ... 279..394B. Дои:10.1086/161900.
- ^ Бухлер, Дж. Р. (1993). "Подход динамических систем к нелинейным звездным пульсациям". Астрофизика и космическая наука. 210 (1–2): 9–31. Bibcode:1993Ap и SS.210 .... 9B. Дои:10.1007 / BF00657870.
- ^ Гукенхаймер, Джон; Холмс, Филип; Слемрод, М. (1984). «Нелинейные колебания динамических систем и бифуркации векторных полей». Журнал прикладной механики. 51 (4): 947. Bibcode:1984JAM .... 51..947G. Дои:10.1115/1.3167759.
- ^ Coullet, P.H .; Шпигель, Э. А. (1983). «Амплитудные уравнения для систем с конкурирующими неустойчивостями». Журнал SIAM по прикладной математике. 43 (4): 776–821. Дои:10.1137/0143052.
- ^ Шпигель, Э. А. (1985). «Космические аритмии». Хаос в астрофизике. С. 91–135. Дои:10.1007/978-94-009-5468-7_3. ISBN 978-94-010-8914-2.
- ^ Бюхлер, Дж. Роберт; Ковач, Геза (1987). «Выбор мод в звездных пульсаторах. II. Применение к моделям RR Lyrae». Астрофизический журнал. 318: 232. Bibcode:1987ApJ ... 318..232B. Дои:10.1086/165363.
- ^ Ван Хоолст, Т. (1996). «Влияние нелинейностей на одиночную колебательную моду звезды». Астрономия и астрофизика. 308: 66. Bibcode:1996 А и А ... 308 ... 66 В.
- ^ Бюхлер, Дж. Роберт; Москалик, Павел; Ковач, Геза (1990). "Обзор пульсаций модели ударных цефеид". Астрофизический журнал. 351: 617. Bibcode:1990ApJ ... 351..617B. Дои:10.1086/168500.
- ^ Ван Хоолст, Тим (1994). «Уравнения связанных мод и амплитудные уравнения для неадиабатических, нерадиальных колебаний звезд». Астрономия и астрофизика. 292: 471. Bibcode:1994А & А ... 292..471В.
- ^ Buchler, J. R .; Goupil, M. -J .; Хансен, К. Дж. (1997). «О роли резонансов в нерадиальных пульсаторах». Астрономия и астрофизика. 321: 159. Bibcode:1997A и A ... 321..159B.
- ^ Kolláth, Z .; Buchler, J. R .; Szabó, R .; Csubry, Z .; Morel, T .; Barban, C .; Бауден, Ф .; Hekker, S .; Samadi, R .; Де Риддер, Дж .; Weiss, W .; Auvergne, M .; Баглин, А. (2002). «Нелинейные модели биений цефеид и лиры RR». Астрономия и астрофизика. 385 (3): 932–939. arXiv:astro-ph / 0110076. Bibcode:2002A&A ... 385..932K. Дои:10.1051/0004-6361:20020182.
- ^ Кристи, Роберт Ф. (1964). «Расчет звездной пульсации» (PDF). Обзоры современной физики. 36 (2): 555–571. Bibcode:1964РвМП ... 36..555С. Дои:10.1103 / RevModPhys.36.555.
- ^ Кокс, Артур Н .; Браунли, Роберт Р .; Эйлерс, Дональд Д. (1966). "Нестационарный метод расчета диффузии излучения и гидродинамики". Астрофизический журнал. 144: 1024. Bibcode:1966ApJ ... 144.1024C. Дои:10.1086/148701.
- ^ Бухлер, Дж. Р. (1993). "Подход динамических систем к нелинейным звездным пульсациям". Астрофизика и космическая наука. 210 (1–2): 9–31. Bibcode:1993Ap и SS.210 .... 9B. Дои:10.1007 / BF00657870.
- ^ Шпигель, Э.А. (1985). «Космические аритмии». Хаос в астрофизике. С. 91–135. Дои:10.1007/978-94-009-5468-7_3. ISBN 978-94-010-8914-2.
- ^ Klapp, J .; Goupil, M. J .; Бухлер, Дж. Р. (1985). «Амплитудные уравнения для неадиабатических нелинейных звездных пульсаторов. II - Приложение к реалистичным резонансным моделям цефеид». Астрофизический журнал. 296: 514. Bibcode:1985ApJ ... 296..514K. Дои:10.1086/163471.
- ^ Konig, M .; Paunzen, E .; Тиммер, Дж. (1999). "О неправильном временном поведении переменной звезды Р. Скути". Ежемесячные уведомления Королевского астрономического общества. 303 (2): 297. Bibcode:1999МНРАС.303..297К. Дои:10.1046 / j.1365-8711.1999.02216.x.
- ^ Айкава, Тосики (1990). «Прерывистый хаос в последовательности субгармонических бифуркаций моделей звездных пульсаций». Астрофизика и космическая наука. 164 (2): 295–307. Bibcode:1990Ap и SS.164..295A. Дои:10.1007 / BF00658831.
- ^ Ковач, Геза; Бюхлер, Дж. Роберт (1988). "Регулярные и нерегулярные нелинейные пульсации в моделях цефеид популяции II". Астрофизический журнал. 334: 971. Bibcode:1988ApJ ... 334..971K. Дои:10.1086/166890..
- ^ Бухлер, Дж. Р., Гупил М. Дж. И Ковач Г., 1987 г.,Касательные бифуркации и перемежаемость пульсаций моделей цефеид популяции II, Physics Letters A 126, 177–180.
- ^ Айкава, Тошики (1987). "Прерывистый переход Помо-Манневиля к хаосу в моделях гидродинамических пульсаций". Астрофизика и космическая наука. 139 (2): 281–293. Bibcode:1987Ap и SS.139..281A. Дои:10.1007 / BF00644357.
- ^ Letellier, C .; Gouesbet, G .; Суфи, Ф .; Buchler, J. R .; Коллат, З. (1996). «Хаос в переменных звездах: топологический анализ пульсаций модели W Vir». Хаос. 6 (3): 466–476. Bibcode:1996 Хаос ... 6..466L. Дои:10.1063/1.166189. PMID 12780277.
- ^ Packard, N.H .; Кратчфилд, Дж. П .; Farmer, J.D .; Шоу, Р. С. (1980). «Геометрия из временного ряда». Письма с физическими проверками. 45 (9): 712. Bibcode:1980ПхРвЛ..45..712П. Дои:10.1103 / PhysRevLett.45.712.
- ^ Бюхлер, Дж. Роберт; Серр, Тьерри; Коллат, Золтан; Маттей, Джанет (1995). "Хоатическая пульсирующая звезда: Случай Р. Скути". Письма с физическими проверками. 74 (6): 842–845. Bibcode:1995ПхРвЛ..74..842Б. Дои:10.1103 / PhysRevLett.74.842. PMID 10058863.
- ^ Packard, N.H .; Кратчфилд, Дж. П .; Farmer, J.D .; Шоу, Р. С. (1980). «Геометрия из временного ряда». Письма с физическими проверками. 45 (9): 712. Bibcode:1980ПхРвЛ..45..712П. Дои:10.1103 / PhysRevLett.45.712.
- ^ Леонов, Г.А. (2013). "Шильниковский хаос в лоренц-подобных системах". Международный журнал бифуркаций и хаоса. 23 (3): 1350058. Bibcode:2013IJBC ... 2350058L. Дои:10.1142 / S0218127413500582.
- ^ Бюхлер, Дж. Роберт; Коллат, Золтан; Кадмус, Роберт Р. (2004). "Доказательства низкоразмерного хаоса в полуправильных переменных звездах". Астрофизический журнал. 613 (1): 532–547. arXiv:astro-ph / 0406109. Bibcode:2004ApJ ... 613..532B. Дои:10.1086/422903.



