Модель замещения - Substitution model
В биологии модель замещения, также называемый модели эволюции последовательности ДНК, находятся Марковские модели которые описывают изменения в течение эволюционного времени. Эти модели описывают эволюционные изменения макромолекул (например, Последовательности ДНК ) представлен как последовательность символов (A, C, G и T в случае ДНК ). Модели замещения используются для расчета вероятность из филогенетические деревья с помощью множественное выравнивание последовательностей данные. Таким образом, модели замещения играют центральную роль в оценке филогении методом максимального правдоподобия, а также Байесовский вывод в филогении. Оценки эволюционных расстояний (количество замен, которые произошли с тех пор, как пара последовательностей расходится от общего предка) обычно рассчитываются с использованием моделей замещения (эволюционные расстояния используются для ввода для дистанционные методы Такие как присоединение соседа ). Модели замещения также занимают центральное место в филогенетические инварианты поскольку их можно использовать для прогнозирования частот шаблонов сайтов с учетом топологии дерева. Модели замещения необходимы для моделирования данных последовательности для группы организмов, связанных определенным деревом.
Топологии филогенетических деревьев и другие параметры
Топологии филогенетических деревьев часто представляют интерес;[1] таким образом, длины ветвей и любые другие параметры, описывающие процесс замещения, часто рассматриваются как мешающие параметры. Однако биологов иногда интересуют другие аспекты модели. Например, длины ветвей, особенно когда эти длины ветвей объединены с информацией из Окаменелости и модель для оценки временных рамок эволюции.[2] Другие параметры модели были использованы для понимания различных аспектов процесса эволюции. В Kа/ Кs соотношение (также называемый ω в моделях замещения кодонов) является параметром, представляющим интерес во многих исследованиях. Kа/ Кs соотношение может быть использовано для изучения действия естественного отбора на белковые кодирующие области;[3] он предоставляет информацию об относительных скоростях нуклеотидных замен, которые изменяют аминокислоты (несинонимичные замены) на те, которые не изменяют кодируемую аминокислоту (синонимичные замены).
Применение к данным последовательности
Большая часть работы над моделями замещения была сосредоточена на ДНК /РНК и белок эволюция последовательности. Модели эволюции последовательности ДНК, где алфавит соответствует четырем нуклеотиды (A, C, G и T), вероятно, самые простые модели для понимания. Модели ДНК также можно использовать для исследования РНК-вирус эволюция; это отражает тот факт, что РНК также имеет алфавит из четырех нуклеотидов (A, C, G и U). Однако модели замещения могут использоваться для алфавитов любого размера; алфавит 20 протеиногенные аминокислоты для белков и смысловые кодоны (т.е. 61 кодон, кодирующий аминокислоты в стандартный генетический код ) для выровненных последовательностей генов, кодирующих белок. Фактически, модели замены могут быть разработаны для любых биологических признаков, которые могут быть закодированы с использованием определенного алфавита (например, аминокислотные последовательности в сочетании с информацией о конформации этих аминокислот в трехмерные белковые структуры[4]).
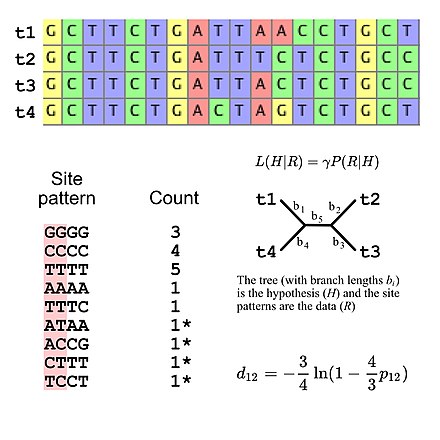
Большинство моделей замен, используемых для эволюционных исследований, предполагают независимость между сайтами (то есть вероятность наблюдения любого конкретного шаблона сайта идентична независимо от того, где шаблон сайта находится в выравнивании последовательностей). Это упрощает расчеты вероятности, потому что необходимо только рассчитать вероятность всех шаблонов сайтов, которые появляются в выравнивании, а затем использовать эти значения для расчета общей вероятности согласования (например, вероятность трех шаблонов сайтов "GGGG" при некоторой модели Эволюция последовательности ДНК - это просто вероятность того, что образец одного сайта "GGGG" возведен в третью степень). Это означает, что модели замещения могут рассматриваться как подразумевающие определенное полиномиальное распределение частот паттернов сайтов. Если мы рассмотрим множественное выравнивание последовательностей с четырьмя последовательностями ДНК, существует 256 возможных паттернов сайтов, поэтому существует 255 степени свободы для частот шаблонов сайта. Впрочем, можно уточнить. ожидаемые частоты паттернов сайтов с использованием пяти степеней свободы при использовании модели эволюции ДНК Джукса-Кантора[5], которая представляет собой простую модель замещения, которая позволяет вычислить ожидаемую частоту паттернов сайтов, только топологию дерева и длины ветвей (с учетом четырех таксонов, неукорененное бифуркационное дерево имеет пять длин ветвей).
Модели замещения также позволяют моделировать данные последовательности, используя Методы Монте-Карло. Смоделированные множественные выравнивания последовательностей могут использоваться для оценки эффективности филогенетических методов.[6] и генерировать нулевое распределение для определенных статистических тестов в области молекулярной эволюции и молекулярной филогенетики. Примеры этих тестов включают тесты на соответствие модели.[7] и «тест SOWH», который можно использовать для изучения топологии дерева.[8][9]
Приложение к морфологическим данным
Тот факт, что модели замещения могут использоваться для анализа любого биологического алфавита, позволил разработать модели эволюции для наборов фенотипических данных.[10] (например, морфологические и поведенческие черты). Обычно это «0». используется для обозначения отсутствия признака, а «1» используется для обозначения наличия признака, хотя также возможно подсчитывать символы с использованием нескольких состояний. Используя эту структуру, мы могли бы кодировать набор фенотипов как двоичные строки (это можно обобщить на k-state строки для символов с более чем двумя состояниями) перед анализом в соответствующем режиме. Это можно проиллюстрировать на примере «игрушки»: мы можем использовать двоичный алфавит для оценки следующих фенотипических признаков «имеет перья», «откладывает яйца», «имеет мех», «теплокровен» и «способен приводить в действие. полет". В этом примере игрушки колибри будет иметь последовательность 11011 (большинство других птицы будет такая же строка), страусы будет иметь последовательность 11010, крупный рогатый скот (и большинство других земель млекопитающие ) будет 00110, а летучие мыши будет иметь 00111. Вероятность филогенетического дерева затем может быть рассчитана с использованием этих бинарных последовательностей и соответствующей модели замещения. Существование этих морфологических моделей позволяет анализировать матрицы данных с ископаемыми таксонами, используя только морфологические данные.[11] или комбинация морфологических и молекулярных данных[12] (последние засчитываются как недостающие данные для таксонов ископаемых).
Существует очевидное сходство между использованием молекулярных и фенотипических данных в области кладистика и анализ морфологических признаков с использованием модели замещения. Тем не менее, был шумные дебаты[а] в систематика сообщества по вопросу о том, следует ли рассматривать кладистический анализ как «свободный от моделей». Область кладистики (определяемая в самом строгом смысле) поддерживает использование максимальная экономия критерий филогенетического вывода.[13] Многие кладисты отвергают позицию, согласно которой максимальная экономия основана на модели замещения, и (во многих случаях) они оправдывают использование экономии, используя философию Карл Поппер.[14] Однако существование «эквивалентных экономичности» моделей[15] (т. е. модели замещения, которые дают дерево максимальной экономии при использовании для анализа) позволяют рассматривать экономию как модель замещения.[1]
Молекулярные часы и единицы времени
Обычно длина ветви филогенетического дерева выражается как ожидаемое количество замен на сайт; если эволюционная модель показывает, что каждое место в пределах наследственной последовательности обычно испытывает Икс замены к тому времени, когда он эволюционирует в последовательность конкретного потомка, тогда предок и потомок считаются разделенными длиной ветви Икс.
Иногда длину ветви измеряют в геологических годах. Например, летопись окаменелостей может дать возможность определить количество лет между предком и потомком. Поскольку некоторые виды развиваются быстрее, чем другие, эти два показателя длины ветви не всегда находятся в прямой зависимости. Ожидаемое количество замен на сайт в год часто обозначается греческой буквой мю (μ).
Говорят, что модель имеет строгий молекулярные часы если ожидаемое количество замен в год μ постоянно, независимо от того, эволюция какого вида изучается. Важным следствием строгих молекулярных часов является то, что количество ожидаемых замен между предковым видом и любым из его современных потомков не должно зависеть от того, какой вид-потомок исследуется.
Обратите внимание, что предположение о строгих молекулярных часах часто нереалистично, особенно в течение длительных периодов эволюции. Например, хотя грызуны генетически очень похожи на приматы, они претерпели гораздо большее количество замен за расчетное время с момента расхождения в некоторых регионах геном.[16] Это могло быть связано с их более короткими время поколения,[17] выше скорость метаболизма, усиление структурирования населения, повышение скорости видообразование, или меньше размер тела.[18][19] При изучении древних событий, таких как Кембрийский взрыв в предположении молекулярных часов, плохое совпадение между кладистический и филогенетические данные часто наблюдаются. Была проведена некоторая работа над моделями, допускающими переменную скорость эволюции.[20][21]
Модели, которые могут учитывать изменчивость скорости молекулярных часов между различными эволюционными линиями филогении, называются «расслабленными» в противоположность «строгим». В таких моделях можно предположить, что скорость коррелирована или нет между предками и потомками, а вариация скорости между линиями может быть получена из многих распределений, но обычно применяются экспоненциальные и логнормальные распределения. Есть особый случай, называемый «локальными молекулярными часами», когда филогения делится, по крайней мере, на две части (наборы родословных), и в каждом из них применяются строгие молекулярные часы, но с разной скоростью.
Обратимые во времени и стационарные модели
Многие полезные модели замещения обратимый во времени; с точки зрения математики, модель не заботится о том, какая последовательность является предком, а какая потомком, пока все другие параметры (например, число замен на сайт, которое ожидается между двумя последовательностями) остаются постоянными.
Когда выполняется анализ реальных биологических данных, обычно нет доступа к последовательностям предковых видов, только к современным видам. Однако, когда модель обратима во времени, не имеет значения, какой вид был предком. Вместо этого филогенетическое дерево может быть укоренено с использованием любого из видов, повторно укоренено позже на основе новых знаний или оставлено без корней. Это потому, что не существует «особых» видов, все виды в конечном итоге произошли друг от друга с одинаковой вероятностью.
Модель обратима во времени тогда и только тогда, когда она удовлетворяет свойству (обозначения поясняются ниже)
или, что то же самое, подробный баланс свойство,
для каждого я, j, и т.
Обратимость во времени не следует путать с стационарность. Модель стационарна, если Q не меняется со временем. Приведенный ниже анализ предполагает стационарную модель.
Математика моделей замещения
Стационарные, нейтральные, независимые модели конечных узлов (предполагающие постоянную скорость эволюции) имеют два параметра: π, равновесный вектор базовых (или символьных) частот и матрица скоростей, Q, который описывает скорость, с которой базы одного типа превращаются в базы другого типа; элемент за я ≠ j скорость, при которой база я идет на базу j. Диагонали Q матрицы выбираются так, чтобы сумма строк равнялась нулю:
Вектор-строка равновесия π должно быть аннулировано матрицей скорости Q:
Матричная функция перехода - это функция от длин ветвей (в некоторых единицах времени, возможно, в подстановках) до матрица условных вероятностей. Обозначается . Запись в яth столбец и jth ряд, , - вероятность, по прошествии времени т, что есть база j в данной позиции, при условии наличия базы я в этой позиции в момент времени 0. Когда модель обратима во времени, это может быть выполнено между любыми двумя последовательностями, даже если одна не является предком другой, если вам известна общая длина ветви между ними.
Асимптотические свойства пij(t) таковы, что пij(0) = δij, где δij это Дельта Кронекера функция. То есть нет изменений в базовой композиции между последовательностью и самой собой. С другой стороны, или, другими словами, по мере того, как время уходит в бесконечность, вероятность найти базу j в данной позиции была база я в этой позиции изначально идет к равновесной вероятности того, что существует базовая j в этой позиции, независимо от исходной базы. Кроме того, отсюда следует, что для всех т.
Матрица перехода может быть вычислена из матрицы скоростей с помощью матричное возведение в степень:
куда Qп это матрица Q умножить на себя достаточно раз, чтобы дать пth мощность.
Если Q является диагонализуемый, матричная экспонента может быть вычислен прямо: пусть Q = U−1 ΛU быть диагонализацией Q, с
где Λ - диагональная матрица и где являются собственными значениями Q, каждый повторяется в соответствии с его кратностью. потом
где диагональная матрица еΛt дан кем-то
Обобщенное время обратимое
Обобщенная обратимая во времени (ОТО) - это наиболее общая нейтральная, независимая, с конечными узлами, обратимая во времени модель из возможных. Впервые в общем виде он был описан Симон Таваре в 1986 г.[22] В публикациях модель ОТО часто называют общей моделью с обратимым временем;[23] ее также называют моделью REV.[24]
Параметры ОТО для нуклеотидов состоят из вектора равновесной базовой частоты, , что дает частоту, с которой каждая база встречается на каждом сайте, и матрица скоростей
Поскольку модель должна быть обратимой во времени и должна приближаться к равновесным частотам нуклеотидов (оснований) в течение длительного времени, каждая скорость ниже диагонали равна обратной скорости выше диагонали, умноженной на равновесное соотношение двух оснований. Таким образом, нуклеотидный GTR требует 6 параметров скорости замещения и 4 параметра равновесной базовой частоты. Поскольку сумма четырех частотных параметров должна быть равна 1, имеется только 3 свободных частотных параметра. Общее количество 9 свободных параметров часто сокращается до 8 параметров плюс , общее количество замен в единицу времени. При замере времени в заменах (= 1) осталось всего 8 свободных параметров.
В общем, чтобы вычислить количество параметров, вы подсчитываете количество записей над диагональю в матрице, то есть для n значений признаков на сайт. , а затем добавьте п-1 для равновесных частот и вычтем 1, потому что фиксированный. Ты получаешь
Например, для аминокислотной последовательности (всего 20 «стандартных» аминокислоты которые составляют белки ), вы найдете 208 параметров. Однако при изучении кодирующих областей генома чаще работают с кодон модель замещения (кодон состоит из трех оснований и кодирует одну аминокислоту в белке). Есть кодонов, что дает 2078 свободных параметров. Однако скорости переходов между кодонами, которые различаются более чем на одно основание, часто принимают равными нулю, сокращая количество свободных параметров только до параметры. Еще одна распространенная практика - уменьшить количество кодонов, запретив стоп (или ерунда ) кодоны. Это биологически разумное предположение, поскольку включение стоп-кодонов означало бы, что вычисляется вероятность обнаружения смыслового кодона. по истечении времени учитывая, что наследственный кодон будет включать возможность прохождения через состояние с преждевременным стоп-кодоном.
Альтернатива (и обычно используется[23][25][26][27]) способ записать матрицу мгновенных скоростей ( матрица) для нуклеотидной модели GTR:
В матрица нормализована так .
Это обозначение легче понять, чем обозначение, первоначально используемое Таваре, поскольку все параметры модели соответствуют либо параметрам «заменяемости» ( через , который также можно записать в обозначениях ) или к равновесию нуклеотид частоты . Обратите внимание, что нуклеотиды в Матрицы написаны в алфавитном порядке. Другими словами, матрица вероятностей перехода для матрица выше будет:
В некоторых публикациях нуклеотиды записываются в другом порядке (например, некоторые авторы предпочитают сгруппировать два пурины вместе и двое пиримидины вместе; смотрите также модели эволюции ДНК ). Эти различия в обозначениях делают важным четкое определение порядка состояний при написании матрица.
Ценность этого обозначения в том, что мгновенная скорость изменения нуклеотида к нуклеотиду всегда можно записать как , куда возможность обмена нуклеотидов и и - равновесная частота нуклеотид. В приведенной выше матрице используются буквы через для параметров заменяемости в интересах удобочитаемости, но эти параметры также можно записывать систематическим образом с использованием обозначение (например, , , и так далее).
Обратите внимание, что порядок индексов нуклеотидов для параметров обменяемости не имеет значения (например, ), но значения матрицы вероятностей перехода - нет (т. е. это вероятность наблюдения A в последовательности 1 и C в последовательности 2, когда эволюционное расстояние между этими последовательностями равно в то время как - вероятность наблюдения C в последовательности 1 и A в последовательности 2 на одном и том же эволюционном расстоянии).
Произвольно выбранные параметры взаимозаменяемости (например, ) обычно устанавливается на значение 1, чтобы повысить удобочитаемость оценок параметров заменяемости (поскольку это позволяет пользователям выражать эти значения относительно выбранного параметра возможности обмена).Практика выражения параметров заменяемости в относительных терминах не представляет проблем, поскольку матрица нормализована. Нормализация позволяет (время) в матричном возведении в степень должны быть выражены в единицах ожидаемых замен на сайт (стандартная практика в молекулярной филогенетике). Это эквивалентно утверждению, что вы устанавливаете скорость мутации. до 1) и сокращение количества свободных параметров до восьми. В частности, существует пять параметров свободной заменяемости ( через , которые выражаются относительно фиксированной в этом примере) и три параметра равновесной базовой частоты (как описано выше, только три значения должны быть указаны, потому что сумма должна быть равна 1).
Альтернативные обозначения также упрощают понимание подмоделей модели GTR, которые просто соответствуют случаям, когда параметры взаимозаменяемости и / или равновесной базовой частоты должны принимать одинаковые значения. Был назван ряд конкретных подмоделей, во многом основанных на их оригинальных публикациях:
| Модель | Параметры заменяемости | Параметры базовой частоты | Ссылка |
|---|---|---|---|
| JC69 (или JC) | Джакс и Кантор (1969)[5] | ||
| F81 | все бесплатные ценности | Фельзенштейн (1981)[28] | |
| K2P (или K80) | (трансверсии ), (переходы ) | Кимура (1980)[29] | |
| HKY85 | (трансверсии ), (переходы ) | все бесплатные ценности | Hasegawa et al. (1985)[30] |
| K3ST (или K81) | ( трансверсии ), ( трансверсии ), (переходы ) | Кимура (1981)[31] | |
| TN93 | (трансверсии ), ( переходы ), ( переходы ) | все бесплатные ценности | Тамура и Ней (1993)[32] |
| SYM | все параметры заменяемости бесплатно | Жарких (1994)[33] | |
| GTR (или REV[24]) | все параметры заменяемости бесплатно | все бесплатные ценности | Таваре (1986)[22] |
Существует 203 возможных способа ограничения параметров заменяемости для формирования подмоделей ОТО.[34] начиная с JC69[5] и F81[28] модели (где все параметры заменяемости равны) к SYM[33] модель и полное ОТО[22] (или REV[24]) модель (где все параметры взаимозаменяемости свободны). Равновесные базовые частоты обычно трактуются двумя разными способами: 1) все значения должны быть равными (т. е. ); или 2) все значения рассматриваются как свободные параметры. Хотя равновесные базовые частоты могут быть ограничены другими способами, большинство из них ограничивает связь, но не все ценности нереалистичны с биологической точки зрения. Возможное исключение - обеспечение симметрии прядей.[35] (т. е. ограничение и но позволяя ).
Альтернативные обозначения также позволяют легко увидеть, как модель GTR может быть применена к биологическим алфавитам с большим пространством состояний (например, аминокислоты или же кодоны ). Можно записать набор частот равновесных состояний как , , ... и набор параметров заменяемости () для любого алфавита состояния персонажей. Эти значения можно использовать для заполнения матрицу, установив недиагональные элементы, как показано выше (общее обозначение будет ), задав диагональные элементы к отрицательной сумме недиагональных элементов в той же строке и нормализации. Очевидно, за аминокислоты и за кодоны (при условии стандартный генетический код ). Однако общность этой нотации полезна, потому что можно использовать сокращенные алфавиты для аминокислот. Например, можно использовать и кодировать аминокислоты путем перекодирования аминокислот с использованием шести категорий, предложенных Маргарет Дейхофф. Сокращенные аминокислотные алфавиты рассматриваются как способ уменьшить влияние вариации и насыщенности композиции.[36]
Механистические и эмпирические модели
Основное различие в эволюционных моделях состоит в том, сколько параметров оценивается каждый раз для рассматриваемого набора данных и сколько из них оценивается один раз для большого набора данных. Механистические модели описывают все замены как функцию ряда параметров, которые оцениваются для каждого анализируемого набора данных, предпочтительно с использованием максимальная вероятность. Это имеет то преимущество, что модель может быть адаптирована к особенностям конкретного набора данных (например, различные систематические ошибки в составе ДНК). Проблемы могут возникнуть, когда используется слишком много параметров, особенно если они могут компенсировать друг друга (это может привести к неидентифицируемости[37]). Тогда часто бывает, что набор данных слишком мал, чтобы дать достаточно информации для точной оценки всех параметров.
Эмпирические модели создаются путем оценки многих параметров (обычно всех элементов матрицы скорости, а также частот символов, см. Модель GTR выше) из большого набора данных. Затем эти параметры фиксируются и будут повторно использоваться для каждого набора данных. Это имеет то преимущество, что эти параметры можно оценить более точно. Обычно невозможно оценить все записи матрица замещения только из текущего набора данных. С другой стороны, параметры, оцененные на основе данных обучения, могут быть слишком общими и, следовательно, плохо соответствовать какому-либо конкретному набору данных. Потенциальным решением этой проблемы является оценка некоторых параметров на основе данных с использованием максимальная вероятность (или каким-то другим способом). В исследованиях эволюции белков равновесные частоты аминокислот (с использованием однобуквенные коды IUPAC для аминокислот для обозначения их равновесных частот) часто оцениваются по данным[38] при сохранении фиксированной матрицы заменяемости. Помимо общепринятой практики оценки частот аминокислот по данным, методы оценки параметров обменности[39] или отрегулируйте матрица[40] для эволюции белка были предложены другие способы.
Поскольку крупномасштабное секвенирование генома по-прежнему дает очень большое количество последовательностей ДНК и белков, имеется достаточно данных для создания эмпирических моделей с любым числом параметров, включая эмпирические модели кодонов.[41] Из-за проблем, упомянутых выше, два подхода часто комбинируются, оценивая большинство параметров один раз на крупномасштабных данных, в то время как несколько оставшихся параметров затем корректируются в соответствии с рассматриваемым набором данных. В следующих разделах дается обзор различных подходов, используемых для моделей на основе ДНК, белков или кодонов.
Модели замещения ДНК
Предложены первые модели эволюции ДНК. Джукс и Кантор[5] в 1969 году. Модель Джукса-Кантора (JC или JC69) предполагает равные скорости переходов, а также равные равновесные частоты для всех оснований, и это простейшая подмодель модели ОТО. В 1980 г. Мотоо Кимура представила модель с двумя параметрами (К2П или К80[29]): один для переход и один для трансверсия ставка. Год спустя, Кимура представила вторую модель (K3ST, K3P или K81[31]) с тремя типами замены: один для переход ставка, одна на ставку трансверсии сохраняющие сильные / слабые свойства нуклеотидов ( и , назначенный Кимура[31]), и один для скорости трансверсии сохраняющие амино / кето-свойства нуклеотидов ( и , назначенный Кимура[31]). 1981 г., Йозеф Фельзенштейн предложила четырехпараметрическую модель (F81[28]), в которой скорость замещения соответствует равновесной частоте целевого нуклеотида. Хасегава, Кишино и Яно объединили две последние модели в пятипараметрическую модель (HKY[30]). После этих новаторских усилий многие дополнительные подмодели модели ОТО были введены в литературу (и стали широко использоваться) в 1990-х годах.[32][33] Другие модели, выходящие за рамки модели ОТО определенным образом, также были разработаны и уточнены несколькими исследователями.[42][43]
Почти все модели замещения ДНК являются механистическими моделями (как описано выше). Небольшое количество параметров, которые необходимо оценить для этих моделей, позволяет оценить эти параметры на основе данных. Это также необходимо, потому что модели эволюции последовательности ДНК часто различаются между организмами и между генами внутри организмов. Последнее может отражать оптимизацию путем выбора для конкретных целей (например, быстрое выражение или стабильность информационной РНК), или это может отражать нейтральные вариации в паттернах замещения. Таким образом, в зависимости от организма и типа гена, вероятно, необходимо адаптировать модель к этим обстоятельствам.
Модели замещения с двумя состояниями
Альтернативный способ анализа данных последовательности ДНК - перекодировать нуклеотиды в пурины (R) и пиримидины (Y);[44][45] эту практику часто называют RY-кодированием.[46] Вставки и делеции в нескольких выравниваниях последовательностей также могут быть закодированы как двоичные данные.[47] и проанализированы с использованием модели двух состояний.[48][49]
Простейшая модель эволюции последовательностей с двумя состояниями называется моделью Кавендера-Фарриса или модели Кавендера-Фарриса.Нейман (CFN) модель; Название этой модели отражает тот факт, что она была независимо описана в нескольких различных публикациях.[50][51][52] Модель CFN идентична модели Джукса-Кантора, адаптированной к двум состояниям, и даже была реализована как модель "JC2" в популярном IQ-ДЕРЕВО программный пакет (использование этой модели в IQ-TREE требует кодирования данных как 0 и 1, а не R и Y; популярные ПАУП * программный пакет может интерпретировать матрицу данных, содержащую только R и Y, как данные, подлежащие анализу с использованием модели CFN). Бинарные данные также легко анализировать с помощью филогенетических Преобразование Адамара.[53] Альтернативная модель с двумя состояниями позволяет параметрам равновесной частоты R и Y (или 0 и 1) принимать значения, отличные от 0,5, путем добавления одного свободного параметра; эта модель по-разному называется CFu[44] или GTR2 (в IQ-TREE).
Модели замещения аминокислот
Для многих анализов, особенно для более длинных эволюционных расстояний, эволюция моделируется на уровне аминокислот. Поскольку не все замены ДНК также изменяют кодируемую аминокислоту, информация теряется при просмотре аминокислот, а не нуклеотидных оснований. Однако несколько преимуществ говорят в пользу использования информации об аминокислотах: ДНК гораздо более склонна показывать композиционный уклон чем аминокислоты, не все позиции в ДНК развиваются с одинаковой скоростью (несинонимичный мутации с меньшей вероятностью закрепятся в популяции, чем синоним единицы), но, вероятно, наиболее важно то, что из-за этих быстро развивающихся позиций и ограниченного размера алфавита (всего четыре возможных состояния) ДНК страдает от большего количества обратных замен, что затрудняет точную оценку более длинных эволюционных расстояний.
В отличие от моделей ДНК, аминокислотные модели традиционно являются эмпирическими моделями. Они были впервые предложены Дайхоффом и его сотрудниками в 1960-х и 1970-х годах, когда они оценили коэффициенты замещения на основе сопоставлений белков с идентичностью не менее 85% (первоначально с очень ограниченными данными[54] и, в конечном итоге, завершится Dayhoff PAM модель 1978 г.[55]). Это минимизировало шансы увидеть множественные замены на площадке. Из оценочной матрицы скорости была получена серия матриц вероятности замены, известных под такими названиями, как PAM 250. Матрицы логарифма шансов на основе Dayhoff. PAM модели обычно использовались для оценки значимости результатов поиска гомологии, хотя BLOSUM матрицы[56] заменили PAM в этом контексте матрицы логарифмических шансов, поскольку матрицы BLOSUM кажутся более чувствительными на различных эволюционных расстояниях, в отличие от PAM логарифмические матрицы шансов.[57]
Матрица Dayhoff PAM была источником параметров обменной способности, используемых в одном из первых анализов филогении методом максимального правдоподобия, в котором использовались данные о белках.[58] и модель PAM (или улучшенная версия модели PAM под названием DCMut[59]) продолжает использоваться в филогенетике. Однако ограниченное количество выравниваний, использованных для создания модели PAM (отражающее ограниченное количество данных о последовательностях, доступных в 1970-х годах), почти наверняка увеличивало дисперсию некоторых параметров матрицы скорости (в качестве альтернативы, белки, использованные для создания модели PAM, могли быть нерепрезентативный набор). Несмотря на это, очевидно, что модель PAM редко так хорошо подходит для большинства наборов данных, как более современные эмпирические модели (Keane et al. 2006[60] протестировали тысячи позвоночное животное, протеобактериальный, и архей белков, и они обнаружили, что модель Dayhoff PAM лучше всего подходит не более чем для <4% белков).
Начиная с 1990-х годов быстрое расширение баз данных последовательностей за счет улучшенных технологий секвенирования привело к оценке многих новых эмпирических матриц. В самых ранних попытках использовались методы, аналогичные тем, которые использовались Dayhoff, с использованием крупномасштабного сопоставления базы данных белков для создания новой матрицы логарифмических шансов.[61] и модель JTT (Джонс-Тейлор-Торнтон).[62] Быстрое увеличение вычислительной мощности за это время (с учетом таких факторов, как Закон Мура ) сделало возможным оценивать параметры эмпирических моделей, используя максимальная вероятность (например, WAG[38] и LG[63] модели) и другие методы (например, VT[64] и PMB[65] модели).
Модель отсутствия общего механизма (NCM) и максимальная экономия
В 1997 году Таффли и Стил[66] описали модель, которую они назвали моделью отсутствия общего механизма (NCM). Топология максимальная вероятность дерево для определенного набора данных с учетом модели NCM идентично топологии оптимального дерева для тех же данных с учетом максимальная экономия критерий. Модель NCM предполагает, что все данные (например, гомологичные нуклеотиды, аминокислоты или морфологические признаки) связаны общим филогенетическим деревом. потом параметры вводятся для каждого гомологичного символа, где количество последовательностей. Это можно рассматривать как оценку отдельного параметра скорости для каждой пары знак × ветвь в наборе данных (обратите внимание, что количество ветвей в полностью разрешенном филогенетическом дереве равно ). Таким образом, количество свободных параметров в модели NCM всегда превышает количество гомологичных символов в матрице данных, а модель NCM подвергается критике как последовательно «чрезмерно параметризованная».[67]
Рекомендации
- ^ а б Steel M, Penny D (июнь 2000 г.). «Экономия, вероятность и роль моделей в молекулярной филогенетике». Молекулярная биология и эволюция. 17 (6): 839–50. Дои:10.1093 / oxfordjournals.molbev.a026364. PMID 10833190.
- ^ Бромхэм Л. (май 2019 г.). «Шесть невозможных вещей перед завтраком: предположения, модели и вера в молекулярное датирование». Тенденции в экологии и эволюции. 34 (5): 474–486. Дои:10.1016 / j.tree.2019.01.017. PMID 30904189.
- ^ Ян З., Белявский JP (декабрь 2000 г.). «Статистические методы определения молекулярной адаптации». Тенденции в экологии и эволюции. 15 (12): 496–503. Дои:10.1016 / s0169-5347 (00) 01994-7. ЧВК 7134603. PMID 11114436.
- ^ Перрон Ю., Козлов А.М., Стаматакис А., Голдман Н., Моал И.Х. (сентябрь 2019 г.). Пупко Т. (ред.). «Моделирование структурных ограничений на эволюцию белка с помощью конформационных состояний боковой цепи». Молекулярная биология и эволюция. 36 (9): 2086–2103. Дои:10.1093 / molbev / msz122. ЧВК 6736381. PMID 31114882.
- ^ а б c d Юкс TH, Кантор CH (1969). «Эволюция белковых молекул». В Манро HN (ред.). Метаболизм белков млекопитающих. 3. Эльзевир. С. 21–132. Дои:10.1016 / b978-1-4832-3211-9.50009-7. ISBN 978-1-4832-3211-9.
- ^ Huelsenbeck JP, Hillis DM (1 сентября 1993 г.). «Успех филогенетических методов в случае четырех таксонов». Систематическая биология. 42 (3): 247–264. Дои:10.1093 / sysbio / 42.3.247. ISSN 1063-5157.
- ^ Гольдман Н. (февраль 1993 г.). «Статистические тесты моделей замещения ДНК». Журнал молекулярной эволюции. 36 (2): 182–98. Bibcode:1993JMolE..36..182G. Дои:10.1007 / BF00166252. PMID 7679448. S2CID 29354147.
- ^ Swofford D.L. Olsen G.J. Уодделл П.Дж. Хиллис Д.М. 1996. "Филогенетический вывод". в Молекулярная систематика (ред. Хиллис Д.М. Мориц К. Мейбл Б.К.) 2-е изд. Сандерленд, Массачусетс: Синауэр. п. 407–514. ISBN 978-0878932825
- ^ Черч С.Х., Райан Дж. Ф., Данн К. В. (ноябрь 2015 г.). «Автоматизация и оценка теста SOWH с SOWHAT». Систематическая биология. 64 (6): 1048–58. Дои:10.1093 / sysbio / syv055. ЧВК 4604836. PMID 26231182.
- ^ Льюис П.О. (2001-11-01). «Вероятностный подход к оценке филогении по дискретным данным морфологического характера». Систематическая биология. 50 (6): 913–25. Дои:10.1080/106351501753462876. PMID 12116640.
- ^ Ли М.С., Кау А., Наиш Д., Дайк Г.Дж. (май 2014 г.). «Морфологические часы в палеонтологии и среднемеловое происхождение кроны Авес». Систематическая биология. 63 (3): 442–9. Дои:10.1093 / sysbio / syt110. PMID 24449041.
- ^ Ronquist F, Klopfstein S, Vilhelmsen L, Schulmeister S, Murray DL, Rasnitsyn AP (декабрь 2012 г.). «Тотальный подход к датированию по окаменелостям, применяемый к раннему облучению перепончатокрылых». Систематическая биология. 61 (6): 973–99. Дои:10.1093 / sysbio / sys058. ЧВК 3478566. PMID 22723471.
- ^ Брауэр, А.В.З. (2016). "Мы все кладисты?" в Уильямс, Д., Шмитт, М., и Уиллер, К. (ред.). Будущее филогенетической систематики: наследие Вилли Хеннига (Специальный выпуск серии томов Ассоциации систематики, книга 86). Издательство Кембриджского университета. С. 88-114. ISBN 978-1107117648
- ^ Фаррис Дж. С., Клюге А. Г., Карпентер Дж. М. (01.05.2001). Олмстед Р. (ред.). "Поппер и правдоподобие против" Поппера *"". Систематическая биология. 50 (3): 438–444. Дои:10.1080/10635150119150. ISSN 1076-836X. PMID 12116585.
- ^ Гольдман, Ник (декабрь 1990). "Вывод максимального правдоподобия филогенетических деревьев с особым упором на модель процесса Пуассона замены ДНК и на анализ экономичности". Систематическая зоология. 39 (4): 345–361. Дои:10.2307/2992355. JSTOR 2992355.
- ^ Гу X, Ли WH (сентябрь 1992 г.). «Более высокие показатели замены аминокислот у грызунов, чем у человека». Молекулярная филогенетика и эволюция. 1 (3): 211–4. Дои:10.1016 / 1055-7903 (92) 90017-Б. PMID 1342937.
- ^ Ли У.Х., Эллсуорт Д.Л., Крушкал Дж., Чанг Б.Х., Хьюетт-Эммет Д. (февраль 1996 г.). «Скорость замены нуклеотидов у приматов и грызунов и гипотеза эффекта времени поколения». Молекулярная филогенетика и эволюция. 5 (1): 182–7. Дои:10.1006 / mpev.1996.0012. PMID 8673286.
- ^ Мартин А.П., Палумби С.Р. (май 1993 г.). «Размер тела, скорость метаболизма, время генерации и молекулярные часы». Труды Национальной академии наук Соединенных Штатов Америки. 90 (9): 4087–91. Bibcode:1993ПНАС ... 90.4087М. Дои:10.1073 / пнас.90.9.4087. ЧВК 46451. PMID 8483925.
- ^ Ян З., Нильсен Р. (апрель 1998 г.). «Синонимичные и несинонимичные вариации скорости ядерных генов млекопитающих». Журнал молекулярной эволюции. 46 (4): 409–18. Bibcode:1998JMolE..46..409Y. CiteSeerX 10.1.1.19.7744. Дои:10.1007 / PL00006320. PMID 9541535. S2CID 13917969.
- ^ Кишино Х., Торн Дж. Л., Бруно В. Дж. (Март 2001 г.). «Выполнение метода оценки времени расхождения в рамках вероятностной модели эволюции скорости». Молекулярная биология и эволюция. 18 (3): 352–61. Дои:10.1093 / oxfordjournals.molbev.a003811. PMID 11230536.
- ^ Торн Дж. Л., Кишино Н., Художник И. С. (декабрь 1998 г.). «Оценка скорости эволюции скорости молекулярной эволюции». Молекулярная биология и эволюция. 15 (12): 1647–57. Дои:10.1093 / oxfordjournals.molbev.a025892. PMID 9866200.
- ^ а б c Таваре С. «Некоторые вероятностные и статистические проблемы анализа последовательностей ДНК» (PDF). Лекции по математике в естественных науках. 17: 57–86.
- ^ а б Ян З (2006). Вычислительная молекулярная эволюция. Оксфорд: Издательство Оксфордского университета. ISBN 978-1-4294-5951-8. OCLC 99664975.
- ^ а б c Ян З (июль 1994). «Оценка закономерностей нуклеотидных замен». Журнал молекулярной эволюции. 39 (1): 105–11. Bibcode:1994JMolE..39..105Y. Дои:10.1007 / BF00178256. PMID 8064867. S2CID 15895455.
- ^ Своффорд, Д.Л., Олсен, Г.Дж., Уодделл, П.Дж., Хиллис, Д.М. (1996) Филогенетический вывод. В: Hillis, D.M., Moritz, C. и Mable, B.K., Eds., Molecular Systematics, 2nd Edition, Sinauer Associates, Sunderland (MA), 407-514. ISBN 0878932828 ISBN 978-0878932825
- ^ Фельзенштейн Дж (2004). Вывод филогении. Сандерленд, Массачусетс: Sinauer Associates. ISBN 0-87893-177-5. OCLC 52127769.
- ^ Swofford DL, Bell CD (1997). "(Проект) PAUP * руководство". Получено 31 декабря 2019.
- ^ а б c Фельзенштейн Дж (ноябрь 1981 г.). «Эволюционные деревья из последовательностей ДНК: подход максимального правдоподобия». Журнал молекулярной эволюции. 17 (6): 368–76. Bibcode:1981JMolE..17..368F. Дои:10.1007 / BF01734359. PMID 7288891. S2CID 8024924.
- ^ а б Кимура М. (декабрь 1980 г.). «Простой метод оценки скорости эволюции замен оснований посредством сравнительных исследований нуклеотидных последовательностей». Журнал молекулярной эволюции. 16 (2): 111–20. Bibcode:1980JMolE..16..111K. Дои:10.1007 / BF01731581. PMID 7463489. S2CID 19528200.
- ^ а б Хасэгава М., Кишино Х., Яно Т. (октябрь 1985 г.). «Датирование расщепления человека и обезьяны по молекулярным часам митохондриальной ДНК». Журнал молекулярной эволюции. 22 (2): 160–74. Bibcode:1985JMolE..22..160H. Дои:10.1007 / BF02101694. PMID 3934395. S2CID 25554168.
- ^ а б c d Кимура М. (январь 1981 г.). «Оценка эволюционных расстояний между гомологичными нуклеотидными последовательностями». Труды Национальной академии наук Соединенных Штатов Америки. 78 (1): 454–8. Bibcode:1981PNAS ... 78..454K. Дои:10.1073 / pnas.78.1.454. ЧВК 319072. PMID 6165991.
- ^ а б Тамура К., Ней М. (май 1993 г.). «Оценка количества нуклеотидных замен в контрольной области митохондриальной ДНК у человека и шимпанзе». Молекулярная биология и эволюция. 10 (3): 512–26. Дои:10.1093 / oxfordjournals.molbev.a040023. PMID 8336541.
- ^ а б c Жарких А (сентябрь 1994 г.). «Оценка эволюционных расстояний между нуклеотидными последовательностями». Журнал молекулярной эволюции. 39 (3): 315–29. Bibcode:1994JMolE..39..315Z. Дои:10.1007 / BF00160155. PMID 7932793. S2CID 33845318.
- ^ Huelsenbeck JP, Larget B, Alfaro ME (июнь 2004 г.). «Выбор байесовской филогенетической модели с использованием обратимого скачка цепи Маркова Монте-Карло». Молекулярная биология и эволюция. 21 (6): 1123–33. Дои:10.1093 / молбев / мш123. PMID 15034130.
- ^ Яп В.Б., Пахтер Л. (апрель 2004 г.). «Выявление горячих точек эволюции в геномах грызунов». Геномные исследования. 14 (4): 574–9. Дои:10.1101 / гр.1967904. ЧВК 383301. PMID 15059998.
- ^ Susko E, Roger AJ (сентябрь 2007 г.). «Об алфавитах сокращенных аминокислот для филогенетических выводов». Молекулярная биология и эволюция. 24 (9): 2139–50. Дои:10,1093 / мольбэв / мсм144. PMID 17652333.
- ^ Пончиано Дж. М., Берли Дж. Г., Браун Э. Л., Конус М. Л. (декабрь 2012 г.). «Оценка идентифицируемости параметров в филогенетических моделях с использованием клонирования данных». Систематическая биология. 61 (6): 955–72. Дои:10.1093 / sysbio / sys055. ЧВК 3478565. PMID 22649181.
- ^ а б Уилан С., Голдман Н. (май 2001 г.). «Общая эмпирическая модель эволюции белков, полученная из нескольких семейств белков с использованием подхода максимального правдоподобия». Молекулярная биология и эволюция. 18 (5): 691–9. Дои:10.1093 / oxfordjournals.molbev.a003851. PMID 11319253.
- ^ Braun EL (июль 2018 г.). «Модель эволюции, основанная на физико-химических свойствах аминокислот, выявляет различия между белками». Биоинформатика. 34 (13): i350 – i356. Дои:10.1093 / биоинформатика / bty261. ЧВК 6022633. PMID 29950007.
- ^ Голдман Н., Уилан С. (ноябрь 2002 г.). «Новое использование равновесных частот в моделях эволюции последовательности». Молекулярная биология и эволюция. 19 (11): 1821–31. Дои:10.1093 / oxfordjournals.molbev.a004007. PMID 12411592.
- ^ Kosiol C, Holmes I, Goldman N (июль 2007 г.). «Эмпирическая модель кодонов для эволюции белковой последовательности». Молекулярная биология и эволюция. 24 (7): 1464–79. Дои:10.1093 / молбев / msm064. PMID 17400572.
- ^ Тамура К. (июль 1992 г.). «Оценка количества замен нуклеотидов при сильных смещениях трансверсии перехода и содержания G + C». Молекулярная биология и эволюция. 9 (4): 678–87. Дои:10.1093 / oxfordjournals.molbev.a040752. PMID 1630306.
- ^ Халперн А.Л., Бруно В.Дж. (июль 1998 г.). «Эволюционные расстояния для последовательностей, кодирующих белок: моделирование частот сайт-специфичных остатков». Молекулярная биология и эволюция. 15 (7): 910–7. Дои:10.1093 / oxfordjournals.molbev.a025995. PMID 9656490. S2CID 7332698.
- ^ а б Браун Э.Л., Кимбалл RT (август 2002 г.). Kjer K (ред.). «Изучение базальных птичьих дивергенций с митохондриальными последовательностями: сложность модели, выборка таксона и длина последовательности». Систематическая биология. 51 (4): 614–25. Дои:10.1080/10635150290102294. PMID 12228003.
- ^ Филлипс М.Дж., Делсук Ф., Пенни Д. (июль 2004 г.). «Филогения в масштабе генома и обнаружение систематических ошибок». Молекулярная биология и эволюция. 21 (7): 1455–8. Дои:10.1093 / молбев / мш137. PMID 15084674.
- ^ Исикава С.А., Инагаки Ю., Хашимото Т. (январь 2012 г.). «RY-кодирование и неоднородные модели могут улучшить выводы максимального правдоподобия из данных нуклеотидных последовательностей с параллельной неоднородностью состава». Эволюционная биоинформатика в Интернете. 8: 357–71. Дои:10.4137 / EBO.S9017. ЧВК 3394461. PMID 22798721.
- ^ Simmons MP, Ochoterena H (июнь 2000 г.). «Пробелы как символы в последовательном филогенетическом анализе». Систематическая биология. 49 (2): 369–81. Дои:10.1093 / sysbio / 49.2.369. PMID 12118412.
- ^ Юрий Т., Кимбалл Р.Т., Харшман Дж., Боуи Р.С., Браун М.Дж., Хойновски Дж.Л. и др. (Март 2013 г.). «Экономия и модельный анализ инделей в ядерных генах птиц выявляют конгруэнтные и несовместимые филогенетические сигналы». Биология. 2 (1): 419–44. Дои:10.3390 / biology2010419. ЧВК 4009869. PMID 24832669.
- ^ Хоуде П., Браун Е.Л., Нарула Н., Минджарес Ю., Мирараб С. (2019-07-06). «Филогенетический сигнал инделей и неоавианское излучение». Разнообразие. 11 (7): 108. Дои:10.3390 / d11070108.
- ^ Кавендер JA (август 1978 г.). «Таксономия с уверенностью». Математические биологические науки. 40 (3–4): 271–280. Дои:10.1016/0025-5564(78)90089-5.
- ^ Фаррис Дж.С. (1 сентября 1973 г.). «Вероятностная модель для вывода эволюционных деревьев». Систематическая биология. 22 (3): 250–256. Дои:10.1093 / sysbio / 22.3.250. ISSN 1063-5157.
- ^ Нейман, Дж. Молекулярные исследования эволюции: источник новых статистических проблем. В молекулярных исследованиях эволюции: источник новых статистических проблем; Gupta, S.S., Yackel, J., Eds .; New York Academic Press: Нью-Йорк, Нью-Йорк, США, 1971; С. 1–27.
- ^ Уодделл П.Дж., Пенни Д., Мур Т. (август 1997 г.). «Сопряжения Адамара и моделирование эволюции последовательностей с неравными скоростями по сайтам». Молекулярная филогенетика и эволюция. 8 (1): 33–50. Дои:10.1006 / mpev.1997.0405. PMID 9242594.
- ^ Дайхофф МО, Эк Р.В., Парк К.М. (1969). «Модель эволюционного изменения белков». В Dayhoff MO (ред.). Атлас последовательности и структуры белков. 4. С. 75–84.
- ^ Дайхофф МО, Шварц Р.М., Оркатт Британская Колумбия (1978). «Модель эволюционного изменения белков» (PDF). В Dayhoff MO (ред.). Атлас последовательности и структуры белков. 5. С. 345–352.
- ^ Хеникофф С., Хеникофф Дж. Г. (ноябрь 1992 г.). «Матрицы аминокислотных замен из белковых блоков». Труды Национальной академии наук Соединенных Штатов Америки. 89 (22): 10915–9. Bibcode:1992PNAS ... 8910915H. Дои:10.1073 / пнас.89.22.10915. ЧВК 50453. PMID 1438297.
- ^ Альтшул С.Ф. (март 1993 г.). «Система оценки белков, чувствительная на всех эволюционных дистанциях». Журнал молекулярной эволюции. 36 (3): 290–300. Bibcode:1993JMolE..36..290A. Дои:10.1007 / BF00160485. PMID 8483166. S2CID 22532856.
- ^ Кишино Х., Мията Т., Хасегава М. (август 1990 г.). «Максимально правдоподобный вывод филогении белков и происхождения хлоропластов». Журнал молекулярной эволюции. 31 (2): 151–160. Bibcode:1990JMolE..31..151K. Дои:10.1007 / BF02109483. S2CID 24650412.
- ^ Kosiol C, Goldman N (февраль 2005 г.). «Различные версии матрицы ставок Dayhoff». Молекулярная биология и эволюция. 22 (2): 193–9. Дои:10.1093 / molbev / msi005. PMID 15483331.
- ^ Keane TM, Creevey CJ, Pentony MM, Naughton TJ, Mclnerney JO (март 2006 г.). «Оценка методов выбора аминокислотной матрицы и их использования на эмпирических данных показывает, что специальные допущения для выбора матрицы не оправданы». BMC Эволюционная биология. 6 (1): 29. Дои:10.1186/1471-2148-6-29. ЧВК 1435933. PMID 16563161.
- ^ Гоннет Г. Х., Коэн М. А., Беннер С. А. (июнь 1992 г.). «Исчерпывающее сопоставление всей базы данных последовательностей белков». Наука. 256 (5062): 1443–5. Bibcode:1992Научный ... 256.1443G. Дои:10.1126 / science.1604319. PMID 1604319.
- ^ Джонс Д. Т., Тейлор В. Р., Торнтон Дж. М. (июнь 1992 г.). «Быстрое создание матриц данных о мутациях из белковых последовательностей». Компьютерные приложения в биологических науках. 8 (3): 275–82. Дои:10.1093 / биоинформатика / 8.3.275. PMID 1633570.
- ^ Le SQ, Gascuel O (июль 2008 г.). «Улучшенная матрица общих аминокислотных замен». Молекулярная биология и эволюция. 25 (7): 1307–20. Дои:10.1093 / molbev / msn067. PMID 18367465.
- ^ Мюллер Т., Вингрон М. (декабрь 2000 г.). «Моделирование аминокислотного замещения». Журнал вычислительной биологии. 7 (6): 761–76. Дои:10.1089/10665270050514918. PMID 11382360.
- ^ Veerassamy S, Smith A, Tillier ER (декабрь 2003 г.). «Модель вероятности перехода для аминокислотных замен из блоков». Журнал вычислительной биологии. 10 (6): 997–1010. Дои:10.1089/106652703322756195. PMID 14980022.
- ^ Таффли С., Сталь М (май 1997 г.). «Связи между максимальной вероятностью и максимальной экономией при простой модели подмены сайта». Вестник математической биологии. 59 (3): 581–607. Дои:10.1007 / bf02459467. PMID 9172826. S2CID 189885872.
- ^ Держатель М.Т., Льюис П.О., Своффорд Д.Л. (июль 2010 г.). «Информационный критерий акаике не выберет модель отсутствия общего механизма». Систематическая биология. 59 (4): 477–85. Дои:10.1093 / sysbio / syq028. PMID 20547783.
Хорошая модель для филогенетического вывода должна быть достаточно богатой, чтобы иметь дело с источниками шума в данных, но оценка ML, проводимая с использованием моделей с явно завышенными параметрами, может привести к совершенно неверным выводам. Модель NCM, безусловно, слишком богата параметрами, чтобы служить оправданием использования экономии, основанной на том, что она является оценкой машинного обучения в рамках общей модели.
внешняя ссылка
Примечания
- ^ Ссылка описывает полемику #ParsimonyGate, которая представляет собой конкретный пример дискуссии о философской природе критерия максимальной экономии. #ParsimonyGate - это реакция в Твиттере на передовую статью в журнале Cladistics, опубликованную Обществом Вилли Хеннига. В редакционной статье говорится, что «... эпистемологической парадигмой этого журнала является экономия», и утверждается, что существуют философские причины предпочесть экономию другим методам филогенетического вывода. Поскольку другие методы филогенетического вывода (т.












































































