График Титца - Википедия - Tietzes graph
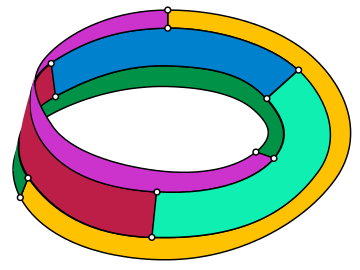
| График Титце | |
|---|---|
 Граф Титце | |
| Вершины | 12 |
| Края | 18 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 3 |
| Автоморфизмы | 12 (D6 ) |
| Хроматическое число | 3 |
| Хроматический индекс | 4 |
| Характеристики | Кубический Снарк |
| Таблица графиков и параметров | |
в математический поле теория графов, График Титце является ненаправленный кубический граф с 12 вершинами и 18 ребрами. Генрих Франц Фридрих Титце, который в 1910 г. показал, что Лента Мебиуса можно разделить на шесть областей, которые все соприкасаются друг с другом - три вдоль границы полосы и три вдоль ее центральной линии - и, следовательно, эти графики встроенный на ленту Мёбиуса может потребоваться шесть цвета.[1] Граничные сегменты областей подразделения Титце (включая сегменты вдоль границы самой ленты Мёбиуса) образуют вложение графа Титце.
Связь с графом Петерсена
График Титце можно составить из Граф Петерсена заменив одну из его вершин на треугольник.[2][3]Как и граф Титце, граф Петерсена образует границу шести взаимно соприкасающихся областей, но на проективная плоскость а не на ленте Мёбиуса. Если вырезать отверстие из этого подразделения проективной плоскости, окружающего единственную вершину, окруженная вершина заменяется треугольником границ области вокруг отверстия, что дает ранее описанную конструкцию графа Титце.
Гамильтоничность
И граф Титце, и граф Петерсена являются максимально негамильтонова: у них нет Гамильтонов цикл, но любые две несмежные вершины можно соединить гамильтоновым путем.[2] Граф Титце и граф Петерсена - единственные 2-вершинно-связанный кубические негамильтоновы графы с 12 или менее вершинами.[4]
В отличие от графика Петерсена, график Титце не гипогамильтониан: удаление одной из трех вершин треугольника образует меньший граф, который остается негамильтоновым.
Раскраска кромок и идеальные сочетания
Краска окраски График Титце требует четырех цветов; то есть его хроматический индекс равен 4. Точно так же ребра графа Титце можно разделить на четыре совпадения, но не меньше.
График Титце соответствует части определения язвить: это кубический безмостовой граф который нельзя раскрашивать по 3 краям. Однако некоторые авторы ограничивают снарки графами без 3-циклов и 4-циклов, и в соответствии с этим более ограничительным определением граф Титце не является снарком. Граф Титце изоморфен графу J3, часть бесконечной семьи цветок snarks введен Р. Айзексом в 1975 г.[5]
В отличие от графа Петерсена, граф Титце покрывается четырьмя идеальное соответствие. Это свойство играет ключевую роль в доказательстве того, что проверка того, можно ли покрыть граф четырьмя точными сопоставлениями, является НП-полный.[6]
Дополнительные свойства
График Титце имеет хроматическое число 3, хроматический индекс 4, обхват 3 и диаметр 3. число независимости равно 5. Его группа автоморфизмов имеет порядок 12 и изоморфна группа диэдра D6, группа симметрий шестиугольник, включая как вращения, так и отражения. Эта группа имеет две орбиты размера 3 и одну размера 6 на вершинах, поэтому этот граф не является вершинно-транзитивный.
Галерея

В хроматическое число графа Титце равно 3.

В хроматический индекс графа Титце равно 4.
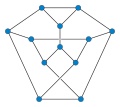
Граф Титце имеет номер перехода 2 и является 1-планарный.

Трехмерное вложение графа Титце.
Смотрите также
- Граф Дюрера и Граф Франклина, два других 12-вершинных кубических графа
Примечания
- ^ Титце, Генрих (1910), "Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen" [Несколько замечаний по проблеме раскраски карт на односторонних поверхностях], DMV Годовой отчет, 19: 155–159[постоянная мертвая ссылка ].
- ^ а б Clark, L .; Энтринджер Р. (1983), "Наименьшие максимально негамильтоновы графы", Periodica Mathematica Hungarica, 14 (1): 57–68, Дои:10.1007 / BF02023582
- ^ Вайсштейн, Эрик В. «График Титце». MathWorld.
- ^ Пунним, Наронг; Саенфольфат, Варапорн; Тайта, Сермсри (2007), «Почти гамильтоновы кубические графы» (PDF), Международный журнал компьютерных наук и сетевой безопасности, 7 (1): 83–86
- ^ Айзекс, Р. (1975), "Бесконечные семейства нетривиальных трехвалентных графов, которые не раскрашиваются по Тейту", Амер. Математика. Ежемесячно, Математическая ассоциация Америки, 82 (3): 221–239, Дои:10.2307/2319844, JSTOR 2319844.
- ^ Esperet, L .; Маццуокколо, Г. (2014), "О кубических графах без мостов, чьи ребра не могут быть покрыты четырьмя точными паросочетаниями", Журнал теории графов, 77 (2): 144–157, arXiv:1301.6926, Дои:10.1002 / jgt.21778, МИСТЕР 3246172.




