Описание функции - Википедия - Describing function
В теория систем управления, то описание функции (DF) метод, разработанный Николай Митрофанович Крылов и Николай Боголюбов в 1930-е годы[1][2] и продлен Ральфом Кохенбургером[3] это приблизительная процедура анализа некоторых нелинейное управление проблемы. Он основан на квазилинеаризации, которая представляет собой приближение исследуемой нелинейной системы с помощью линейный инвариантный во времени (LTI) функция передачи это зависит от амплитуда входного сигнала. По определению, передаточная функция истинной системы LTI не может зависеть от амплитуды входной функции, поскольку система LTI линейный. Таким образом, эта зависимость от амплитуды порождает семейство линейных систем, которые объединены в попытке уловить характерные особенности поведения нелинейной системы. Функция описания - один из немногих широко применяемых методов проектирования нелинейных систем, который очень широко используется в качестве стандартного математического инструмента для анализа предельные циклы в контроллеры с обратной связью, например, управление производственными процессами, сервомеханизмы и электронные генераторы.
Метод
Рассмотрим обратную связь вокруг прерывистой (но кусочно-непрерывной) нелинейности (например, усилитель с насыщением или элемент с зона нечувствительности эффекты) в каскаде с медленной стабильной линейной системой. Непрерывная область, в которой отображается обратная связь по нелинейности, зависит от амплитуды выходного сигнала линейной системы. По мере уменьшения выходной амплитуды линейной системы нелинейность может перейти в другую непрерывную область. Это переключение от одной непрерывной области к другой может генерировать периодические колебания. Метод описывающей функции пытается предсказать характеристики этих колебаний (например, их основную частоту), предполагая, что медленная система действует как НЧ или же Bandpass фильтр, который концентрирует всю энергию вокруг одной частоты. Даже если выходной сигнал имеет несколько режимов, метод все равно может дать интуитивное представление о таких свойствах, как частота и, возможно, амплитуда; в этом случае метод описывающей функции можно рассматривать как описывающий Режим скольжения системы обратной связи.
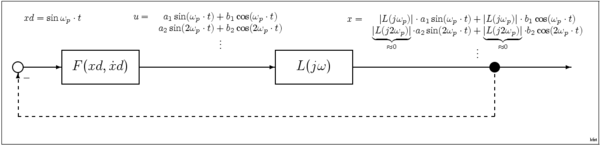
Используя это предположение о низких частотах, отклик системы можно описать одним из семейства синусоидальные формы волны; в этом случае система будет характеризоваться функцией описания синусоидального входа (SIDF) обеспечение отклика системы на вход, состоящий из синусоидальной волны амплитуды A и частоты . Этот SIDF является модификацией функция передачи используется для характеристики линейных систем. В квазилинейной системе, когда входом является синусоидальная волна, на выходе будет синусоидальная волна той же частоты, но с масштабированной амплитудой и сдвинутой фазой, как указано в . Многие системы являются приблизительно квазилинейными в том смысле, что, хотя реакция на синусоидальную волну не является чистой синусоидальной волной, большая часть энергии на выходе действительно находится на той же частоте. как вход. Это связано с тем, что такие системы могут обладать внутренними НЧ или же Bandpass такие характеристики, что гармоники ослабляются естественным образом, или из-за внешних фильтры добавлены для этой цели. Важным применением метода SIDF является оценка амплитуды колебаний в синусоидальном электронные генераторы.
Другие типы описывающих функций, которые использовались, - это DF для входных сигналов уровня и входных сигналов гауссова шума. Хотя это не полное описание системы, DF часто бывает достаточно, чтобы ответить на конкретные вопросы о контроле и устойчивости. Методы пеленгации лучше всего подходят для анализа систем с относительно слабой нелинейностью. В дополнение синусоидальный вход высшего порядка, описывающий функции (HOSIDF), описывают реакцию класса нелинейных систем на гармоники входной частоты синусоидального входа. Функции HOSIDF являются расширением функции SIDF для систем, в которых нелинейности важны в ответе.
Предостережения
Хотя метод описывающих функций может дать достаточно точные результаты для широкого класса систем, он может привести к серьезным ошибкам для других. Например, метод может потерпеть неудачу, если система подчеркивает высшие гармоники нелинейности. Такие примеры были представлены Цыпкиным для ПИФ-паф системы.[4] Довольно похожий пример - генератор с обратной связью, состоящий из неинвертирующего Триггер Шмитта за которым следует инвертирование интегратор который возвращает свой выходной сигнал на вход триггера Шмитта. Выход триггера Шмитта будет прямоугольная форма волны, а интегратор (следующий за ним) будет иметь треугольная форма волны с пиками, совпадающими с переходами в прямоугольной волне. Каждый из этих двух каскадов генератора отстает от сигнала точно на 90 градусов (относительно своего входа). Если провести анализ пеленгации на этой схеме, треугольная волна на входе триггера Шмитта будет заменена ее основной гармоникой (синусоидальной волной), которая, проходя через триггер, вызовет фазовый сдвиг менее 90 градусов (поскольку синусоида вызовет его раньше, чем треугольная волна), поэтому система не будет колебаться таким же (простым) способом.[5]
Также в случае, если условия для Айзермана или же Гипотезы Калмана выполняются, периодических решений по методу описания функции нет,[6][7] но контрпримеры с скрытые периодические аттракторы известны. Контрпримеры к методу описывающих функций могут быть построены для разрывных динамических систем, когда отрезок покоя разрушает предсказанные предельные циклы.[8] Следовательно, применение метода описывающей функции требует дополнительного обоснования.[9][10]
Рекомендации
- ^ Крылов, Н. М .; Н. Боголюбов (1943). Введение в нелинейную механику. Принстон, США: Princeton Univ. Нажмите. ISBN 0691079854. Архивировано из оригинал на 20.06.2013.
- ^ Блакьер, Остин (2012-12-02). Нелинейный системный анализ. Elsevier Science. п. 177. ISBN 978-0323151665.
- ^ Коченбургер, Ральф Дж. (Январь 1950 г.). "Метод частотной характеристики для анализа и синтеза сервомеханизмов контактора". Пер. AIEE. Американский институт инженеров-электриков. 69 (1): 270–284. Дои:10.1109 / t-aiee.1950.5060149.
- ^ Цыпкин, Яков З. (1984). Релейные системы управления. Кембридж: Univ Press.
- ^ Борис Лурье; Пол Энрайт (2000). Классическое управление с обратной связью: с MATLAB. CRC Press. С. 298–299. ISBN 978-0-8247-0370-7.
- ^ Леонов Г.А .; Кузнецов Н.В. (2011). «Алгоритмы поиска скрытых колебаний в задачах Айзермана и Калмана» (PDF). Доклады Математики. 84 (1): 475–481. Дои:10.1134 / S1064562411040120.,
- ^ «Гипотезы Айзермана и Калмана и метод описания функций» (PDF).
- ^ Леонов Г.А .; Кузнецов Н.В. (2018). «О проблеме Келдыша о подавлении флаттера». Материалы конференции AIP. 1959: Изобразительное искусство. число 020002. arXiv:1803.06920. Дои:10.1063/1.5034578.
- ^ Брагин В.О .; Вагайцев В.И .; Кузнецов Н.В .; Леонов Г.А. (2011). "Алгоритмы поиска скрытых колебаний в нелинейных системах. Гипотезы Айзермана и Калмана и схемы Чуа" (PDF). Международный журнал компьютерных и системных наук. 50 (4): 511–543. Дои:10.1134 / S106423071104006X.
- ^ Леонов Г.А .; Кузнецов Н.В. (2013). «Скрытые аттракторы в динамических системах. От скрытых колебаний в задачах Гильберта-Колмогорова, Айзермана и Калмана до скрытых хаотических аттракторов в схемах Чуа». Международный журнал бифуркаций и хаоса. 23 (1): 1330002–219. Bibcode:2013IJBC ... 2330002L. Дои:10.1142 / S0218127413300024.
дальнейшее чтение
- Н. Крылов и Н. Боголюбов: Введение в нелинейную механику, Princeton University Press, 1947 г.
- А. Гелб и В. Э. Вандер Вельде: Описание функций с множеством входов и нелинейное проектирование систем, Макгроу Хилл, 1968.
- Джеймс К. Роберж, Операционные усилители: теория и практика, Глава 6: Нелинейные системы, 1975; бесплатная копия любезно предоставлена MIT OpenCourseWare 6.010 (2013); см. также (1985 г.) видеозапись лекции Робержа о описание функций
- P.W.J.M. Нуйдж, О. Босгра, М. Стейнбух, Синусоидальный вход высшего порядка, описывающий функции для анализа нелинейных систем с гармоническими откликами, механических систем и обработки сигналов, 20 (8), 1883–1904, (2006)



