Треугольная волна - Triangle wave
А треугольная волна или треугольная волна это несинусоидальная форма волны назван в честь своего треугольный форма. Это периодический, кусочно-линейный, непрерывный реальная функция.
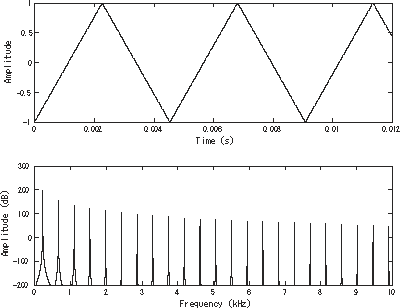
Как прямоугольная волна, треугольная волна содержит только нечетные гармоники. Однако высшие гармоники скатиться намного быстрее, чем в прямоугольной волне (пропорционально обратному квадрату номера гармоники, а не просто обратному).
Определения

Тригонометрические функции
Треугольная волна с периодом п и амплитуда а можно выразить через синус и арксинус (чье значение находится в диапазоне от -π / 2 до π / 2):
Гармоники

Можно аппроксимировать треугольную волну с помощью аддитивный синтез путем суммирования нечетных гармоник основной гармоники при умножении каждой второй нечетной гармоники на -1 (или, что то же самое, изменении ее фазы на π) и умножении амплитуды гармоник на единицу в квадрате их номера моды, п, (что эквивалентно единице в квадрате их относительной частоты к фундаментальный ).
Вышесказанное можно резюмировать математически следующим образом:
где N - количество гармоник, которые нужно включить в приближение, т независимая переменная (например, время для звуковых волн), основная частота, а я - метка гармоники, которая связана с номером ее моды соотношением .
Это бесконечное Ряд Фурье сходится к треугольной волне как N стремится к бесконечности, как показано на анимации.
Функция пола
Еще одно определение треугольной волны с диапазоном от -1 до 1 и периодом п, является:
где это функция пола.
Пилообразная волна
Кроме того, треугольная волна - это абсолютная величина пилообразная волна:
или для диапазона от -1 до 1:
Квадратная волна
Треугольную волну также можно выразить как интеграл из прямоугольная волна:
Операция по модулю
Общее уравнение для треугольной волны с амплитудой и период с использованием операция по модулю и абсолютная величина является:

Отсюда для треугольной волны с амплитудой 5 и периодом 4:
Сдвиг фазы можно получить, изменив значение термин, а вертикальное смещение можно отрегулировать, изменив значение срок.
Поскольку здесь используется только операция по модулю и абсолютное значение, его можно использовать для простой реализации треугольной волны на аппаратной электронике с меньшей мощностью процессора.
Обратите внимание, что во многих языках программирования % оператор является оператором остатка (с тем же знаком, что и делимое), а не оператор по модулю; операцию по модулю можно получить, используя ((x% p) + p)% p на месте x% p. Например, в JavaScript, это приводит к уравнению вида 4 * a / p * Math.abs ((((x-p / 4)% p) + p)% p - p / 2) - a.
Длина дуги
В длина дуги за период для треугольной волны, обозначаемой s, задается через амплитуду а и продолжительность периода п от
Смотрите также
- Список периодических функций
- Синусоидальная волна
- Квадратная волна
- Пилообразная волна
- Пульсовая волна
- Звук
- Функция треугольника
- Волна
- Зигзаг

















