Нелинейное управление - Nonlinear control

Обратная связь система контроля. Желательно управлять системой (часто называемой растение), поэтому его результат соответствует желаемому ссылка сигнал. А датчик контролирует выход и контролер вычитает фактический выходной сигнал из желаемого эталонного выхода и подает этот сигнал ошибки в систему, чтобы приблизить выходной сигнал к эталонному. В нелинейной системе управления по крайней мере один из блоков, система, датчик или контроллер является нелинейным.

Нелинейное управление теория - это область теория управления который имеет дело с системами, которые нелинейный, временной вариант, или оба. Теория управления - это междисциплинарный раздел инженерии и математика это связано с поведением динамические системы с входами, и как изменить выход, изменив вход, используя Обратная связь, прямая связь, или же фильтрация сигналов. Управляемая система называется "растение ». Один из способов сделать вывод системы следует желаемому опорному сигналу является сравнение выходного сигнала завода до желаемого выхода, а также обеспечить Обратная связь заводу, чтобы изменить выход, чтобы приблизить его к желаемому.

Теория управления делится на две части. Теория линейного управления применяется к системам, состоящим из устройств, соответствующих требованиям принцип суперпозиции. Они регулируются линейный дифференциальные уравнения. Основным подклассом являются системы, которые, кроме того, имеют параметры, которые не изменяются со временем, называемые линейный инвариант во времени (LTI) системы. Эти системы могут быть решены с помощью мощных частотная область математические методы очень общего характера, такие как Преобразование Лапласа, преобразование Фурье, Z преобразование, Сюжет Боде, корневой локус, и Критерий устойчивости Найквиста.

Нелинейная теория управления охватывает более широкий класс систем, не подчиняющихся принципу суперпозиции. Это применимо к более реальным системам, потому что все реальные системы управления нелинейны. Эти системы часто регулируются нелинейные дифференциальные уравнения. Математические методы, которые были разработаны для их решения, являются более строгими и гораздо менее общими, часто применимыми только к узким категориям систем. К ним относятся предельный цикл теория Карты Пуанкаре, Теория устойчивости Ляпунова, и описание функций. Если интерес представляют только решения вблизи устойчивой точки, нелинейные системы часто могут быть линеаризованный аппроксимируя их линейной системой, полученной разложением нелинейного решения по серии, а затем можно использовать линейные методы.^[1] Нелинейные системы часто анализируются с использованием численные методы на компьютеры, например, моделирование их работа с использованием язык моделирования. Даже если объект является линейным, нелинейный контроллер часто может иметь привлекательные особенности, такие как более простая реализация, более высокая скорость, большая точность или пониженная энергия управления, что оправдывает более сложную процедуру проектирования.

Примером нелинейной системы управления является термостат -управляемая система отопления. Система отопления здания, такая как печь, нелинейно реагирует на изменения температуры; он либо «включен», либо «выключен», у него нет точного управления в зависимости от разницы температур, которое было бы у пропорционального (линейного) устройства. Поэтому печь выключена до тех пор, пока температура не упадет ниже уставки «включения» термостата, когда он включается. Из-за тепла, добавляемого печью, температура увеличивается до тех пор, пока не достигнет заданного значения «выключение» термостата, который отключает печь, и цикл повторяется. Этот цикл изменения температуры вокруг желаемой температуры называется предельный цикл, и характерна для нелинейных систем управления.

Свойства нелинейных систем

Некоторые свойства нелинейных динамических систем

Они не следуют принципу суперпозиция (линейность и однородность).
У них может быть несколько изолированных точек равновесия.
Они могут проявлять такие свойства, как предельный цикл, бифуркация, хаос.
Конечное время ухода: решения нелинейных систем могут существовать не всегда.

Анализ и управление нелинейными системами

Существует несколько хорошо разработанных методик анализа нелинейных систем обратной связи:

Описание функции метод
Метод фазовой плоскости
Ляпуновская устойчивость анализ
Сингулярное возмущение метод
В Критерий Попова и критерий круга для абсолютной стабильности
Теорема о центральном многообразии
Теорема о малом выигрыше
Анализ пассивности

Также существуют методы проектирования управления для нелинейных систем. Их можно разделить на методы, которые пытаются рассматривать систему как линейную в ограниченном диапазоне операций и используют (хорошо известные) методы линейного проектирования для каждого региона:

Планирование усиления

Те, которые пытаются ввести вспомогательную нелинейную обратную связь таким образом, чтобы систему можно было рассматривать как линейную для целей проектирования управления:

Линеаризация обратной связи

И Ляпунов на основе методов:

Нелинейный анализ обратной связи - проблема Лурье

Блок-схема задачи Лурье

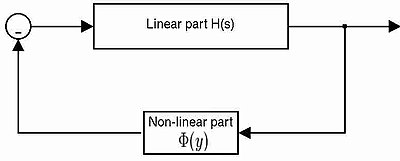
Ранняя задача анализа нелинейной системы обратной связи была сформулирована А. И. Лурье Системы управления, описываемые проблемой Лурье, имеют прямой путь, который является линейным и неизменным во времени, и путь обратной связи, который содержит статическую нелинейность без памяти, возможно изменяющуюся во времени.

Линейная часть может быть охарактеризована четырьмя матрицами (А,B,C,D), а нелинейная часть - Φ (у) с ${ displaystyle { frac { Phi (y)} {y}} in [a, b], quad a$ (секторная нелинейность).

Проблема абсолютной устойчивости

Рассматривать:

(А,B) управляема и (C,А) наблюдается
два действительных числа а, б с а < б, определяя сектор для функции Φ

Проблема Лурье (также известная как проблема абсолютной устойчивости) состоит в том, чтобы вывести условия, включающие только матрицу переноса ЧАС(s) и {а,б} такой, что Икс = 0 - глобально равномерно асимптотически устойчивое положение равновесия системы.

По проблеме абсолютной устойчивости есть две хорошо известные ошибочные гипотезы:

В Гипотеза Айзермана
В Гипотеза Кальмана.

Графически эти гипотезы можно интерпретировать в терминах графических ограничений на график Φ (у) Икс у или также на графике dΦ /dy Икс Φ /у.^[2] Есть контрпримеры к гипотезам Айзермана и Калмана, такие, что нелинейность принадлежит сектору линейной устойчивости и единственное устойчивое равновесие сосуществует со стабильным периодическим решением:скрытое колебание.

Есть две основные теоремы, касающиеся проблемы Лурье, которые дают достаточные условия абсолютной устойчивости:

В критерий круга (продолжение Критерий устойчивости Найквиста для линейных систем)
В Критерий Попова.

Теоретические результаты в нелинейном управлении

Теорема Фробениуса
В Теорема Фробениуса это глубокий результат в дифференциальной геометрии. Применительно к нелинейному управлению он говорит следующее: Для данной системы вида
${ displaystyle { dot {x}} = sum _ {i = 1} ^ {k} f_ {i} (x) u_ {i} (t) ,}$
куда ${ Displaystyle х в R ^ {п}}$ , ${ displaystyle f_ {1}, dots, f_ {k}}$ - векторные поля, принадлежащие распределению ${ displaystyle Delta}$ и ${ Displaystyle и_ {я} (т)}$ - управляющие функции, интегральные кривые ${ displaystyle x}$ ограничены многообразием размерности ${ displaystyle m}$ если ${ Displaystyle OperatorName {span} ( Delta) = m}$ и ${ displaystyle Delta}$ является инволютивный распространение.
Смотрите также

Пассивация обратной связи
Фазовая автоподстройка частоты
Небольшое свойство управления
Рекомендации

^ точка обрезки
^ Naderi, T .; Materassi, D .; Innocenti, G .; Дженезио, Р. (2019). «Пересмотр гипотез Калмана и Айзермана с помощью графической интерпретации». IEEE Transactions по автоматическому контролю. 64 (2): 670–682. Дои:10.1109 / TAC.2018.2849597. ISSN 0018-9286.
дальнейшее чтение

Лурье, А. И .; Постников В. Н. (1944). "К теории устойчивости регулируемых систем" [К теории устойчивости систем управления]. Прикладная Математика и Механика (на русском). 8 (3): 246–248.
Видьясагар, М. (1993). Нелинейный системный анализ (2-е изд.). Энглвудские скалы: Прентис-холл. ISBN 978-0-13-623463-0.
Исидори, А. (1995). Нелинейные системы управления (3-е изд.). Берлин: Springer. ISBN 978-3-540-19916-8.
Халил, Х.К. (2002). Нелинейные системы (3-е изд.). Река Верхнее Седл: Prentice Hall. ISBN 978-0-13-067389-3.
Brogliato, B .; Lozano, R .; Машке, Б .; Эгеланн, О. (2007). Анализ и управление диссипативными системами (2-е изд.). Лондон: Спрингер.
Леонов Г.А .; Кузнецов Н.В. (2011). «Алгоритмы поиска скрытых колебаний в задачах Айзермана и Калмана» (PDF). Доклады Математики. 84 (1): 475–481. Дои:10.1134 / S1064562411040120.
Брагин В.О .; Вагайцев В.И .; Кузнецов Н.В .; Леонов Г.А. (2011). "Алгоритмы поиска скрытых колебаний в нелинейных системах. Гипотезы Айзермана и Калмана и схемы Чуа" (PDF). Международный журнал компьютерных и системных наук. 50 (5): 511–543. Дои:10.1134 / S106423071104006X.
Леонов Г.А., Кузнецов Н.В. (2011). Серхио, Биттанти (ред.). «Аналитико-численные методы исследования скрытых колебаний в нелинейных системах управления». (PDF). Сборники трудов МФБ (документы IFACOnline). Материалы 18-го Всемирного конгресса МФБ. 18 (1): 2494–2505. Дои:10.3182 / 20110828-6-IT-1002.03315. ISBN 9783902661937.
внешняя ссылка

Функции языка Wolfram для нелинейных систем управления

[1] точка обрезки

[2] Naderi, T .; Materassi, D .; Innocenti, G .; Дженезио, Р. (2019). «Пересмотр гипотез Калмана и Айзермана с помощью графической интерпретации». IEEE Transactions по автоматическому контролю. 64 (2): 670–682. Дои:10.1109 / TAC.2018.2849597. ISSN 0018-9286.

[1]

[2]