Модель Дике - Википедия - Dicke model

В Модель Дике фундаментальная модель квантовая оптика, который описывает взаимодействие между свет и иметь значение. В модели Дике свет компонент описывается как одиночная квантовая мода, а иметь значение описывается как набор двухуровневые системы. Когда связь между светом и веществом пересекает критическое значение, модель Дике показывает среднее поле фаза перехода к сверхизлучательная фаза. Этот переход принадлежит Класс универсальности Изинга и была реализована экспериментально в квантовая электродинамика резонатора эксперименты. Хотя сверхизлучательный переход имеет некоторую аналогию с генерация При нестабильности эти два перехода относятся к разным классам универсальности.

Описание

Модель Дике - это квантово-механический модель, описывающая связь между одномодовым резонатором и ${ displaystyle N}$ двухуровневые системы, или эквивалентно ${ displaystyle N}$ спин-½ степени свободы. Модель была впервые представлена ​​в 1973 году компанией К. Хепп и Э. Х. Либ.^[1] Их исследование было вдохновлено новаторской работой Р. Х. Дике на сверхизлучатель излучение света в свободном пространстве ^[2] и назван в его честь.

Как и любая другая модель в квантовой механике, модель Дике включает набор квантовых состояний ( Гильбертово пространство ) и полной энергии оператор (в Гамильтониан ). В Гильбертово пространство модели Дике задается (тензорным произведением) состояний полости и двухуровневых систем. Гильбертово пространство полости можно натянуть на Фока заявляет с ${ displaystyle n}$ фотоны, обозначаемый ${ displaystyle | п rangle}$. Эти состояния могут быть построены из вакуумного состояния ${ Displaystyle | п = 0 rangle}$ используя канонический операторы лестницы, ${ displaystyle a ^ { dagger}}$ и ${ displaystyle a}$, которые добавляют и вычитают фотон из резонатора соответственно. Состояния каждой двухуровневой системы называются вверх и вниз и определяются через вращение операторы ${ displaystyle { vec { sigma}} _ {j} = ( sigma _ {j} ^ {x}, ~ sigma _ {j} ^ {y}, ~ sigma _ {j} ^ {z })}$, удовлетворяя спиновая алгебра ${ displaystyle [ sigma _ {j} ^ {x}, ~ sigma _ {k} ^ {y}] = я hbar sigma _ {j} ^ {z} delta _ {j, k}}$. Здесь ${ displaystyle hbar}$ это Постоянная Планка и ${ Displaystyle J = (0,1,2, ..., N)}$ указывает на конкретную двухуровневую систему.^[3]

В Гамильтониан модели Дике

$${ displaystyle H = hbar omega _ {c} a ^ { dagger} a + omega _ {z} sum _ {j = 1} ^ {N} sigma _ {j} ^ {z} + { frac {2 lambda} { sqrt {N}}} (a + a ^ { dagger}) sum _ {j} sigma _ {j} ^ {x} ;.}$$

(1)

Здесь первый член описывает энергию резонатора и равен произведению энергии одного фотона резонатора. ${ displaystyle hbar omega _ {c}}$ (куда ${ displaystyle omega _ {c}}$ частота резонатора), умноженное на количество фотонов в резонаторе, ${ displaystyle n_ {c} = a ^ { dagger} a}$. Второй член описывает энергию двухуровневых систем, где ${ displaystyle hbar omega _ {z}}$ - разность энергий между состояниями каждой двухуровневой системы. Последний член описывает связь между двухуровневыми системами и резонатором и предполагается, что он пропорционален константе: ${ displaystyle lambda}$, умноженное на величину, обратную квадратному корню из числа двухуровневых систем. Это предположение позволяет получить фазовый переход в пределе ${ displaystyle N to infty}$ (видеть ниже ). Связь можно записать как сумму двух членов: совместное вращение член, сохраняющий число возбуждений и пропорциональный ${ displaystyle a sigma ^ {+} + a ^ { dagger} sigma ^ {-}}$ и противовращающийся срок, пропорциональный ${ displaystyle a sigma ^ {-} + a ^ { dagger} sigma ^ {+}}$, куда ${ Displaystyle sigma ^ { pm} = sigma ^ {x} pm я sigma ^ {y}}$ - операторы спиновой лестницы.

В Гамильтониан в уравнении. 1 предполагает, что все спины идентичны (т.е. имеют одинаковую разность энергий и одинаково связаны с полостью). В этом предположении можно определить макроскопические спиновые операторы ${ Displaystyle S ^ { alpha} = sum _ {j = 1} ^ {N} sigma _ {j} ^ { alpha}}$, с ${ Displaystyle альфа = х, у, г}$, которые удовлетворяют спиновая алгебра, ${ displaystyle [S ^ {x}, S ^ {y}] = я hbar S ^ {z}}$. Используя эти операторы, можно переписать Гамильтониан в уравнении. 1 в качестве

$${ displaystyle H = hbar omega _ {c} a ^ { dagger} a + omega _ {z} S ^ {z} + { frac {2 lambda} { sqrt {N}}} (a + a ^ { dagger}) S ^ {x}.}$$

(2)

Это обозначение упрощает численное исследование модели, поскольку в ней используется один спин-S с ${ Displaystyle S leq N / 2}$, гильбертово пространство которого имеет размер ${ displaystyle 2S + 1}$, скорее, чем ${ displaystyle N}$ спин-1/2, гильбертово пространство которого имеет размер ${ displaystyle 2 ^ {N}}$.

В модели Дике есть один глобальная симметрия,

$${ displaystyle { mathcal {P}} :( a, sigma ^ { pm}) to (-a, - sigma ^ { pm}) ;.}$$

(3)

Потому что ${ displaystyle { mathcal {P}}}$ квадратов к единице (т.е. если применить дважды, он возвращает каждое состояние в исходное состояние), он имеет два собственных значения, ${ displaystyle 1}$ и ${ displaystyle -1}$. Эта симметрия связана с сохраненное количество: четность общего числа возбуждений, ${ Displaystyle P = (- 1) ^ {N_ {ex}}}$, куда

$${ displaystyle N_ {ex} = a ^ { dagger} a + sum _ {j = 1} ^ {N} sigma _ {j} ^ {z} ;.}$$

(4)

Это сохранение четности можно увидеть из того факта, что каждый член в гамильтониане сохраняет число возбуждения, за исключением членов, вращающихся в противоположных направлениях, которые могут изменить число возбуждения только на ${ displaystyle pm 2}$. Состояние модели Дике называется нормальный когда эта симметрия сохраняется, и сверхизлучатель когда эта симметрия спонтанно нарушается.

Связанные модели

Модель Дике тесно связана с другими моделями квантовой оптики. В частности, модель Дике с единой двухуровневой системой, ${ Displaystyle N = 1}$, называется моделью Раби. При отсутствии членов, вращающихся в противоположных направлениях, модель называется Джейнс-Каммингс за ${ Displaystyle N = 1}$ и Тэвис-Каммингс за ${ displaystyle N> 1}$. Эти две модели сохраняют количество возбуждений ${ displaystyle N_ {ex}}$ и характеризуются ${ Displaystyle U (1)}$ симметрия. Спонтанное нарушение этой симметрии приводит к генерации состояния (см. ниже ).

Связь между моделью Дике и другими моделями резюмирована в таблице ниже. ^[4]

Название модели	Условия встречного вращения?	симметрия	Количество двухуровневых систем
Джейнс-Каммингс	нет	${ Displaystyle U (1)}$	${ Displaystyle N = 1}$
Тэвис-Каммингс	нет	${ Displaystyle U (1)}$	${ displaystyle N> 1}$
Модель Раби	да	${ displaystyle { mathcal {P}}}$	${ Displaystyle N = 1}$
Дике	да	${ displaystyle { mathcal {P}}}$	${ displaystyle N> 1}$

Сверхизлучательный фазовый переход

Фигура 1. Схематическое изображение параметра порядка перехода Дике, равного нулю в нормальной фазе и конечному в сверхизлучательной фазе. На вставке показана свободная энергия в нормальной и сверхизлучательной фазах, см. Уравнение. 5.

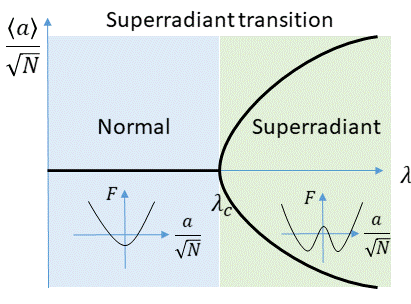
Ранние исследования модели Дике рассматривали ее равновесные свойства.^[1] Эти работы считались пределом ${ displaystyle N to infty}$ (также известный как термодинамический предел) и предположил тепловой функция распределения, ${ Displaystyle Z = ехр (-H / k_ {B} T)}$, куда ${ displaystyle k_ {B}}$ это Постоянная Больцмана и ${ displaystyle T}$ это температура. Было обнаружено, что когда муфта ${ displaystyle lambda}$ пересекает критическое значение ${ displaystyle lambda _ {c}}$модель Дике претерпевает фазовый переход второго рода, известный как сверхизлучательный фазовый переход В их исходном происхождении Хепп и Либ^[1] пренебрегали эффектами встречного вращения членов и, таким образом, фактически рассматривали модель Тэвиса-Каммингса (см. выше). Дальнейшие исследования полной модели Дике показали, что фазовый переход все еще происходит в присутствии вращающихся в противоположных направлениях членов, хотя и при другой критической связи.^[5]

Сверхизлучательный переход спонтанно нарушает симметрию четности, ${ displaystyle { mathcal {P}}}$, определенный в формуле. 3. В параметр порядка этого фазового перехода составляет ${ displaystyle langle {а} rangle / { sqrt {N}}}$. В термодинамическом пределе эта величина стремится к нулю, если система нормальная, или к одному из двух возможных значений, если система сверхизлучательная. Эти два значения соответствуют физическим состояниям поля резонатора с противофазами (см. 3 и, соответственно, к состояниям спина с противоположными ${ displaystyle x}$ составные части). Вблизи сверхизлучательного фазового перехода параметр порядка зависит от ${ displaystyle lambda}$ в качестве ${ displaystyle langle {a} rangle / { sqrt {N}} sim ( lambda _ {c} - lambda) ^ {- 1/2}}$ (см. рис. 1). Эта зависимость соответствует среднему полю критический показатель ${ Displaystyle бета = 1/2}$.

Среднее поле описания перехода

Самый простой способ описать сверхизлучательный переход - использовать среднее поле приближение, в котором операторы поля резонатора заменяются их математическими ожиданиями. В этом приближении, которое является точным в термодинамическом пределе, гамильтониан Дикке уравнения 1 становится суммой независимых членов, каждый из которых действует на другую двухуровневую систему, которую можно диагонализировать независимо. При тепловом равновесии (см. Выше), свободная энергия на двухуровневую систему равна^[6]

$${ displaystyle F left ({ frac { langle a rangle} { sqrt {N}}} = alpha right) = omega _ {c} alpha ^ {2} -k_ {B} T ln left (2 ch left ({ frac { sqrt { omega _ {z} ^ {2} +16 lambda ^ {2} alpha ^ {2}}} {2k_ {B} T }}верно-верно).}$$

(5)

Критическая связь перехода находится из условия ${ Displaystyle dF / d альфа ( альфа = 0) = 0}$, что приводит к

$${ displaystyle lambda _ {c} = { frac {1} {2}} { sqrt { omega _ {c} omega _ {z} coth left ({ frac { hbar omega _ {z}} {2k_ {B} T}} right)}}.}$$

(6)

За ${ displaystyle lambda < lambda _ {c}}$, ${ displaystyle F}$ имеет один минимум, а для ${ displaystyle lambda> lambda _ {c}}$, имеет два минимума (см. вставку к рис. 1). В пределах ${ displaystyle T to 0}$ получаем выражение для критической связи фазового перехода сверхизлучения при нулевой температуре: ${ displaystyle lambda _ {c} = { sqrt { omega _ {c} omega _ {z}}} / 2}$.

Открытая модель Дике

Модель Дикке уравнения. 1 предполагает, что мода резонатора и двухуровневые системы полностью изолированы от внешней среды. В реальных экспериментах это предположение неверно: связь со свободными модами света может вызвать потерю фотонов резонатора и распад двухуровневых системы уровней (т.е. каналы рассеяния). Стоит отметить, что в этих экспериментах используются управляющие поля (например, лазерные поля ) для реализации связи между модой резонатора и двухуровневыми системами. Различные каналы диссипации можно описать, добавив связь с дополнительными степенями свободы окружающей среды. Усредняя по динамике этих внешних степеней свободы, получаем уравнения движения описывая открытая квантовая система В соответствии с обычным приближением Борна-Маркова динамику системы можно описать с помощью квантовое главное уравнение в Линдблад форма ^[7]

$${ displaystyle { frac {d rho} {dt}} = - {i over hbar} [H, rho] + sum _ { alpha} gamma _ { alpha} left (L_ { alpha} rho L _ { alpha} ^ { dagger} - { frac {1} {2}} left {L _ { alpha} ^ { dagger} L _ { alpha}, rho right }верно).}$$

(7)

Здесь, ${ displaystyle rho}$ - матрица плотности системы, ${ displaystyle L _ { alpha}}$ - оператор Линдблада канала распада ${ displaystyle alpha}$, и ${ displaystyle gamma _ { alpha}}$ соответствующая скорость распада. Когда гамильтониан ${ displaystyle H}$ дается формулой. 1, модель называется открытой моделью Дике.

Некоторые общие процессы распада, имеющие отношение к экспериментам, приведены в следующей таблице:

-	Кариес	Атомный распад	Атомная дефазировка	Коллективный распад
Линдбладиан	${ Displaystyle L = а}$	${ Displaystyle L = sigma _ {я} ^ {-}}$	${ Displaystyle L = sigma _ {я} ^ {z}}$	${ Displaystyle L = сумма _ {я} сигма _ {я} ^ {-}}$
Скорость распада	${ displaystyle kappa}$	${ displaystyle gamma _ { downarrow}}$	${ displaystyle gamma _ { phi}}$	${ displaystyle Gamma _ { downarrow}}$

При теоретическом описании модели часто рассматривается стационарное состояние, когда ${ displaystyle d rho / dt = 0}$. В пределах ${ displaystyle N to infty}$, стационарное состояние открытой модели Дике демонстрирует непрерывный фазовый переход, часто называемый неравновесный сверхизлучательный переход. Критические показатели этого перехода такие же, как и у равновесного сверхизлучательного перехода при конечной температуре (и отличаются от сверхизлучательного перехода при нулевой температуре).

Сверхизлучательный переход и сверхизлучение Дике

Фигура 2. Схематическое изображение разницы между сверхизлучением Дике и сверхизлучательным переходом открытой модели Дике.

Сверхизлучательный переход открытой модели Дикке связан с, но отличается от Dicke superradiance (см. рис. 2).

Сверхизлучение Дике - это коллективное явление, при котором многие двухуровневые системы когерентно излучают фотоны в свободном пространстве.^[2][8] Это происходит, если двухуровневые системы изначально подготовлены в возбужденном состоянии и размещены на расстоянии, намного меньшем, чем соответствующая длина волны фотона. В этих условиях спонтанный распад двухуровневых систем становится намного быстрее: двухуровневые системы излучают короткий импульс света с большой амплитудой. В идеальных условиях длительность импульса обратно пропорциональна количеству двухуровневых систем, ${ displaystyle N}$, а максимальная интенсивность излучаемого света масштабируется как ${ displaystyle N ^ {2}}$. Это контрастирует со спонтанным излучением ${ displaystyle N}$ независимые двухуровневые системы, время распада которых не зависит от ${ displaystyle N}$ и где интенсивность импульса масштабируется как ${ displaystyle N}$.

Как объяснялось выше, открытая модель Дике скорее моделирует двухуровневые системы, связанные с квантованным резонатором и управляемые внешним насосом (см.рис. 2). В нормальной фазе интенсивность поля резонатора не зависит от количества атомов. ${ displaystyle N}$, а в фазе сверхизлучения напряженность поля резонатора пропорциональна ${ displaystyle langle a ^ { dagger} a rangle sim N}$.

Законы масштабирования сверхизлучения Дике и сверхизлучательного перехода модели Дикке суммированы в следующей таблице:

	Dicke superradiance[2]	Сверхизлучательный переход модели Дике[1]
Среда	Свободное место	Полость
Продолжительность	Переходный	Устойчивое состояние
Интенсивность поля (нормальная)	${ displaystyle N}$	${ displaystyle 1}$
Напряженность поля (сверхизлучение)	${ displaystyle N ^ {2}}$	${ displaystyle N}$

Экспериментальные реализации

Фигура 3. Схематическое изображение двух схем экспериментальной реализации модели Дике: слева - равновесный подход, основанный на дипольной связи между двумя уровнями, и справа - неравновесный подход, основанный на двухфотонных процессах, а именно, вынужденное комбинационное рассеяние света. Только последняя схема используется для реализации модели Дике.

Простейшая реализация модели Дике связана с дипольной связью двухуровневых атомов в резонаторе (см. Рис. 2, правая панель). В этой системе наблюдению сверхизлучательного перехода препятствуют две возможные проблемы: (1) голая связь между атомами и полостями обычно слабая и недостаточна для достижения критического значения ${ displaystyle lambda _ {c}}$, см. уравнение. 6.^[9] (2) Для точного моделирования физической системы необходимо учитывать ${ displaystyle A ^ {2}}$ условия, которые, согласно непроходимая теорема, может помешать переходу. Оба ограничения можно обойти, применив к атомам внешние насосы и создав эффективную модель Дике в подходящей вращающаяся рама.^[10][11]

В 2010 г. сверхизлучательный переход открытой модели Дике наблюдался экспериментально с использованием нейтральных атомов рубидия, захваченных в оптическом резонаторе.^[12]В этих экспериментах связь между атомами и полостью достигается не за счет прямой дипольной связи между двумя системами. Вместо этого атомы освещаются внешним насосом, который приводит в движение стимулированный Рамановский переход Этот двухфотонный процесс заставляет двухуровневую систему менять свое состояние с вниз к вверх, или же наоборот, и испускать или поглощать фотон в резонатор (см. рис. 3Эксперименты показали, что количество фотонов в резонаторе резко возрастает при переходе интенсивности накачки через критический порог, связанный с критическим взаимодействием модели Дикке.

В экспериментах использовались два разных набора физических состояний в качестве вниз и вверх состояния. В некоторых экспериментах^[13][12],^[14] два состояния соответствуют атомам с разными скоростями или импульсами: вниз состояние имело нулевой импульс и принадлежало Конденсат Бозе-Эйнштейна, в то время как вверх Состояние имело импульс, равный сумме импульса фотона резонатора и импульса фотона накачки.^[15] Напротив, более поздние эксперименты^[16][17] использовали два разных сверхтонкие уровни атомов рубидия в магнитном поле. Последняя реализация позволила исследователям изучить обобщенную модель Дике (см. ниже ). В обоих экспериментах система зависит от времени, и (обобщенный) гамильтониан Дике реализуется в виде рамка, которая вращается на частоте насоса.

Обобщенная модель и генерация

Модель Дике может быть обобщена путем рассмотрения эффектов дополнительных членов в гамильтониане уравнения (2). 1.^[6] Например, недавний эксперимент^[17] реализовал открытую модель Дике с независимо настраиваемыми вращающимися и противовращающимися членами. Помимо сверхизлучательного перехода, это обобщенный Модель Дике может пройти генерация нестабильность, которую назвали инвертированная генерация или же контр-лазер.^[6] Этот переход вызван встречно вращающимися членами модели Дике и наиболее заметен, когда эти члены больше вращающихся.

Неравновесный сверхизлучательный переход и неустойчивость генерации имеют ряд общих черт и различий. Оба перехода относятся к типу среднего поля и могут быть поняты в терминах динамики одной степени свободы. Сверхизлучательный переход соответствует сверхкритическому вилы раздвоение, а неустойчивость генерации соответствует Нестабильность Хопфа. Ключевое различие между этими двумя типами бифуркаций состоит в том, что первый приводит к двум устойчивым решениям, а второй - к периодическим решениям (предельные циклы ). Соответственно, в фазе сверхизлучения поле резонатора статично (в рамках поля накачки), а в фазе генерации оно периодически осциллирует.^[6]

Смотрите также

Рекомендации

Ранняя версия этой страницы была опубликована в Ref.^[18] Пожалуйста, цитируйте эту ссылку в ваших рецензируемых статьях.

Список всех ссылок, используемых в этой статье, с разбивкой по тематике ^[19]

• Оригинальные статьи Дике^[2] и Хепп и Либ^[1]

• Теория ^[10][11] и эксперименты^{[13][12][14][16][17]} открытой модели Дике.

• Обзор книг и статей^{[8][7][5][15][4][6][9]}

-