Динамическая эпистемическая логика - Dynamic epistemic logic
Динамическая эпистемическая логика (DEL) - это логическая структура, связанная с изменением знаний и информации. Как правило, DEL сосредотачивается на ситуациях, связанных с несколькими агенты и изучает, как меняются их знания, когда События происходить. Эти события могут изменить фактические свойства реального мира (их называют онтические события): например, красная карточка окрашивается в синий цвет. Они также могут вызывать изменения знаний без изменения фактических свойств мира (их называют эпистемические события): например, карта раскрывается публично (или в частном порядке) как красная. Первоначально DEL фокусировался на эпистемических событиях. В этой статье мы представляем только некоторые из основных идей исходной среды DEL; более подробную информацию о DEL в целом можно найти в справочниках.
Из-за природы объекта изучения и абстрактного подхода, DEL имеет отношение к многочисленным областям исследований, таким как Информатика (искусственный интеллект ), философия (формальная эпистемология ), экономика (теория игры ) и наука о мышлении. Например, в информатике DEL очень тесно связан с мультиагентные системы, которые представляют собой системы, в которых несколько интеллектуальных агентов взаимодействуют и обмениваются информацией.
Как сочетание динамическая логика и эпистемическая логика, динамическая эпистемологическая логика - молодая область исследований. На самом деле все началось в 1989 году с логики публичных заявлений Plaza.[1] Независимо, Гербранди и Греневельд[2] предложила систему, касающуюся, кроме того, частных объявлений, и это было вдохновлено работой Велтмана.[3] Другая система была предложена ван Дитмаршем, главным вдохновителем которого был Cluedo игра.[4] Но наиболее влиятельной и оригинальной системой была система, предложенная Балтагом, Моссом и Солецким.[5][6] Эта система может работать со всеми типами ситуаций, изученных в вышеперечисленных работах, и ее основная методология концептуально обоснована. В этой статье мы представим некоторые из его основных идей.
Формально DEL расширяет обычные эпистемическая логика путем включения моделей событий для описания действий и оператора обновления продукта, который определяет, как эпистемические модели обновляются в результате выполнения действий, описанных с помощью моделей событий. Эпистемическая логика сначала будет отозван. Затем действия и события войдут в картину, и мы представим структуру DEL.[7]
Эпистемическая логика
Эпистемическая логика это модальная логика имея дело с понятиями знания и веры. Как логика, он связан с пониманием процесса рассуждение о знании и вере: какие принципы, относящиеся к понятиям знания и веры, интуитивно правдоподобны? Как и эпистемология, оно происходит от греческого слова или «эпистема», означающая знание. Эпистемология тем не менее, больше озабочен анализом самого природа и объем знаний, отвечая на такие вопросы, как «Каково определение знания?» или «Как приобретаются знания?». Фактически, эпистемологическая логика выросла из эпистемологии в средние века благодаря усилиям Берли и Оккама.[8] Формальная работа, основанная на модальной логике, положившая начало современным исследованиям эпистемологической логики, датируется только 1962 годом и была создана Hintikka.[9] Затем это вызвало в 1960-х годах дискуссии о принципах знания и убеждений, и многие аксиомы для этих понятий были предложены и обсуждены.[10] Например, аксиомы взаимодействия и часто считаются интуитивными принципами: если агент знает тогда (s) он также верит , или если агент считает , то он знает, что он верит . Совсем недавно такие философские теории были подхвачены исследователями в экономика,[11] искусственный интеллект и теоретическая информатика [12] где рассуждения о знаниях являются центральной темой. Благодаря новому сеттингу, в котором использовалась эпистемологическая логика, появились новые перспективы и новые функции, такие как вычислимость Затем вопросы были добавлены в повестку дня исследования эпистемологической логики.
Синтаксис
Впоследствии, - конечное множество, элементы которого называются агентами и это набор пропозициональных букв.
Эпистемический язык является расширением основного многомодального языка модальная логика с всем известный факт оператор и распределенное знание оператор . Формально эпистемический язык индуктивно определяется следующим грамматика в BNF:
куда , и . В основной эпистемологический язык это язык без операторов общих знаний и распределенных знаний. Формула это сокращение от (для данного ), это сокращение от , это сокращение от и сокращение для .
Групповые понятия: общие, общие и распределенные знания.
В мультиагентной среде есть три важных эпистемологических концепции: общие знания, распределенные знания и общие знания. Понятие общего знания было впервые изучено Льюис в контексте условностей.[13] Затем он был применен к распределенные системы[12] и чтобы теория игры,[14] где это позволяет выразить, что рациональность игроков, правила игры и набор игроков общеизвестны.
Общие знания.
Общие знания означает, что все в группе агентов знает это . Формально это соответствует следующей формуле:
Всем известный факт.
Общие сведения о означает, что все знают но также что все знают, что все знают , что все знают, что все знают, что все знают , и так далее до бесконечности. Формально это соответствует следующей формуле
Поскольку мы не допускаем бесконечного соединения, понятие общего знания должно быть введено в наш язык как примитив.
Прежде чем определять язык с помощью этого нового оператора, мы собираемся привести пример, представленный Льюис это иллюстрирует разницу между понятиями общих знаний и общих знаний. Льюис хотел знать, какие знания необходимы, чтобы утверждение : «Каждый водитель должен ездить по правой стороне» - это условность группы агентов. Другими словами, он хотел знать, какие знания необходимы, чтобы каждый чувствовал себя в безопасности при езде по правой стороне. Предположим, есть только два агента и . Тогда все знают (формально ) недостаточно. В самом деле, возможно, что агент считает возможным, что агент не знает (формально ). В этом случае агент будет небезопасно ехать справа, потому что он может подумать, что агент , не зная , мог ехать налево. Чтобы избежать этой проблемы, мы могли бы предположить, что все знают, что все знают, что (формально ). Этого опять же недостаточно для того, чтобы все чувствовали себя в безопасности при движении справа. В самом деле, возможно, что агент считает возможным, что агент считает возможным, что агент не знает (формально ). В этом случае и от Точка зрения, считает возможным, что , не зная , будет двигаться слева. Так что из Точка зрения, может двигаться и слева (по тем же аргументам, что и выше). Так будет небезопасно ехать справа. Рассуждая по индукции, Льюис показал, что для любого , недостаточно, чтобы водители чувствовали себя в безопасности при движении справа. На самом деле нам нужно бесконечное соединение. Другими словами, нам нужны общие знания о : .
Распространенные знания.
Распределенное знание означает, что если бы агенты полностью использовали свои знания, они бы знали, что держит. Другими словами, знание является распределен среди агентов. Формула читается как «это распределенное знание среди множества агентов. который держит ».
Семантика
Эпистемическая логика - это модальная логика. Итак, что мы называем эпистемическая модель это просто Модель Крипке как определено в модальной логике. Набор - непустое множество, элементы которого называются возможные миры и интерпретация это функция определение того, какие пропозициональные факты (например, «Энн имеет красную карточку») верны в каждом из этих миров. В отношения доступности находятся бинарные отношения для каждого агента ; они предназначены для отражения неопределенности каждого агента (относительно реального мира и неопределенности других агентов). Интуитивно мы имеем когда мир совместим с агентом Информация в мире или, другими словами, когда агент считает этот мир может соответствовать миру (с этой точки зрения). Мы оскорбительно пишем за и обозначает множество миров .
Интуитивно остроконечная эпистемическая модель , куда , представляет с внешней точки зрения, как реальный мир воспринимается агентами .
Для каждой эпистемической модели , каждый и каждый , мы определяем индуктивно следующим условия истины:
| если только | ||
| если только | ||
| если только | ||
| если только | ||
| если только | ||
| если только |
куда это переходное закрытие из : у нас есть это если и только если есть и такой, что и для всех , .
Несмотря на то, что понятие общего убеждения должно быть введено в качестве примитива в языке, мы можем заметить, что определение эпистемических моделей не должно быть изменено, чтобы придать истинное значение операторам общего знания и распределенного знания.
Пример карты:
Игроки , и (обозначающие Энн, Боба и Клэр) сыграйте в карточную игру с тремя картами: красной, зеленой и синей. У каждого из них есть по одной карте, но они не знают карт других игроков. У Энн красная карточка, у Боба зеленая карточка, а у Клэр синяя карточка. Этот пример изображен в заостренной эпистемической модели. представлен ниже. В этом примере и . Каждый мир обозначен пропозициональными буквами, которые истинны в этом мире и соответствует реальному миру. Есть стрелка, указанная агентом из возможного мира в возможный мир когда . Возвратные стрелки опущены, что означает, что для всех и все у нас есть это .

означает: " имеет красную карточку ''
означает: " имеет синюю карту ''
означает: " имеет грин-карту ''
и так далее...
Когда отношения доступности являются отношениями эквивалентности (как в этом примере), и мы имеем, что , мы говорим, что агент не могу отличить Мир из мира (или мир неотличим от мира для агента ). Так, например, не может отличить реальный мир из возможного мира, где имеет синюю карту (), имеет грин-карту () и осталась красная карточка ().
В частности, имеют место следующие утверждения:
«Все агенты знают цвет своей карты».
' знает это имеет либо синюю, либо зеленую карту и что имеет либо синюю, либо зеленую карту ».
'Все это знают имеет красную, зеленую или синюю карту, и это даже известно всем агентам ».
Знание против веры
Мы используем те же обозначения и для знания, и для веры. Следовательно, в зависимости от контекста, либо прочитает "агент Kтеперь это держит »или« агент Believes, что держит ». Принципиальное отличие состоит в том, что, в отличие от знаний, убеждения могут быть неправильный: аксиома справедливо только для знания, но не обязательно для веры. Эта аксиома, называемая аксиомой T (истина), утверждает, что если агент знает предложение, то это утверждение истинно. Его часто считают признаком знания, и он не подвергался серьезным атакам с момента его введения в Theaetetus к Платон.
Понятие знания может соответствовать некоторым другим ограничениям (или аксиомам), таким как : если агент что-то знает, она знает, что знает это. Эти ограничения могут повлиять на характер отношений доступности. который затем может соответствовать некоторым дополнительным свойствам. Итак, теперь мы собираемся определить некоторые конкретные классы эпистемических моделей, которые все добавляют некоторые дополнительные ограничения на отношения доступности. . Этим ограничениям соответствуют определенные аксиомы для оператора знания . Под каждым свойством мы приводим аксиому, которая определяет[15] класс эпистемических фреймов, выполняющих это свойство. ( означает для любого .)
| серийный | |
| D | |
| переходный | |
| 4 | |
| Евклидичность | |
| 5 | |
| рефлексивный | |
| Т | |
| симметричный | |
| B | |
| сливаться | |
| .2 | |
| слабо связанный | |
| .3 | |
| полуевклидов | |
| .3.2 | |
| R1 | |
| .4 |
Мы обсуждаем аксиомы выше. Аксиома 4 утверждает, что если агент знает предложение, то он знает, что он знает его (эта аксиома также известна как «KK-принцип» или «KK-тезис»). В эпистемологии аксиома 4 обычно принимается интерналисты, но не экстерналисты.[16] Тем не менее, аксиома 4 широко принята компьютерными учеными (но также и многими философами, включая Платон, Аристотель, Святой Августин, Спиноза и Шопенгауэр, в качестве Hintikka вспоминает). Более спорная аксиома для логики познания аксиомы 5 для Euclidicity: эта аксиома гласит, что если агент не знает предложение, то она знает, что она не знает об этом. Большинство философов (включая Хинтикку) напали на эту аксиому, поскольку многочисленные примеры из повседневной жизни, кажется, опровергают ее.[17] В общем, аксиома 5 недействительна, если агент ошибается во взглядах, которые могут быть вызваны, например, неправильным восприятием, ложью или другими формами обмана. Аксиома B утверждает, что агент не может считать возможным, что он знает ложное предложение (т. Е. ). Если мы предположим, что аксиомы T и 4 верны, то аксиома B станет жертвой той же атаки, что и аксиома 5, поскольку эта аксиома выводима. Аксиома D утверждает, что убеждения агента последовательны. В сочетании с аксиомой K (где оператор знания заменен оператором убеждения) аксиома D фактически эквивалентна более простой аксиоме D ', которая передает, возможно, более явно, тот факт, что убеждения агента не могут быть противоречивыми: . Другие сложные аксиомы .2, .3, .3.2 и .4 были введены эпистемологическими логиками, такими как Ленцен и Кутчера в 1970-х годах.[10][18] и представлены для некоторых из них как ключевые аксиомы эпистемологической логики. Их можно охарактеризовать с точки зрения аксиом интуитивного взаимодействия, связывающих знания и убеждения.[19]
Аксиоматизация
Гильберт система доказательств K для основного модальная логика определяется следующим аксиомы и правила вывода: для всех ,
| Опора | Все аксиомы и правила вывода логика высказываний |
| K | |
| Nec | Если тогда |
Аксиомы эпистемической логики, очевидно, отображают способ рассуждений агентов. Например, из аксиомы K вместе с правилом вывода Nec следует, что если я знаю () и я знаю что подразумевает ( тогда я знаю что (). Могут быть добавлены более строгие ограничения. Следующее системы доказательства за часто используются в литературе.
| KD45 | = | К + Д + 4 + 5 | S4.2 | = | S4 + .2 | S4.3.2 | = | S4 + .3.2 | S5 | = | S4 + 5 | |||||||||
| S4 | = | К + Т + 4 | S4.3 | = | S4 + .3 | S4.4 | = | S4 + .4 | Br | = | К + Т + В |
Определим множество систем доказательств .
Более того, для всех , определим систему доказательств добавив следующие схемы аксиом и правила вывода к тем из . Для всех ,
| Dis | |
| Смешивание | |
| Ind |
Относительная сила систем доказательства знаний такова:
Итак, все теоремы из также теоремы и . Многие философы утверждают, что в самых общих случаях логика познания или же .[18][20] Обычно в информатике и во многих теориях, разработанных в области искусственного интеллекта, логика веры (доксастический логика) считается и логика познания (эпистемический логика) считается , даже если подходит только для ситуаций, когда агенты не имеют ошибочных убеждений.[17] Флориди предложил логику понятия «информированность», которая в основном отличается от логики знания отсутствием интроспекции для агентов.[21]
Для всех , то класс –Модели или же –Модели - это класс эпистемических моделей, отношения доступности которых удовлетворяют перечисленным выше свойствам, определенным аксиомами или же . Тогда для всех , является звук и сильно полный за w.r.t. класс –Модели и является звук и сильно полный за w.r.t. класс –Модели.
Разрешимость и сложность
В проблема выполнимости для всей введенной логики разрешимый. Мы перечисляем ниже вычислительная сложность проблемы выполнимости для каждого из них. Обратите внимание, что он становится линейным во времени, если в языке есть только конечное число пропозициональных букв. За , если мы ограничимся конечной вложенностью, то проблема выполнимости будет НП-полный для всех рассмотренных модальных логик. Если мы затем ограничим язык наличием только конечного числа примитивных предложений, сложность во всех случаях снизится до линейной по времени.[22][23]
| Логика | общеизвестно | ||
|---|---|---|---|
| К, S4 | PSPACE | PSPACE | EXPTIME |
| KD45 | НП | PSPACE | EXPTIME |
| S5 | НП | PSPACE | EXPTIME |
Вычислительная сложность проблема проверки модели в п во всех случаях.
Добавление динамики
Динамическая эпистемическая логика (DEL) - это логическая структура для моделирования эпистемических ситуаций с участием нескольких агентов и изменений, которые происходят в этих ситуациях в результате поступающей информации или, в более общем смысле, поступающих действий. Методология DEL такова, что она разделяет задачу представления убеждений и знаний агентов на три части:
- Один представляет свои убеждения относительно исходной ситуации благодаря эпистемическая модель;
- Один представляет свои представления о событии, происходящем в этой ситуации благодаря модель событий;
- Один представляет, как агенты обновляют свои представления о ситуации после (или во время) наступления события благодаря обновление продукта.
Как правило, информативным мероприятием может быть публичное объявление для всех агентов формулы. : это публичное объявление и соответствующее обновление составляют динамическую часть. Однако эпистемологические события могут быть намного сложнее простого публичного объявления, включая сокрытие информации для некоторых агентов, обман, ложь, блеф и т. Д. и Т. Д. Эта сложность решается, когда мы вводим понятие модели событий. Сначала мы сосредоточимся на публичных объявлениях, чтобы получить интуитивное представление об основных идеях, лежащих в основе DEL.
Публичные мероприятия
В этом разделе мы предполагаем, что все мероприятия являются публичными. Начнем с конкретного примера, где можно использовать DEL, чтобы лучше понять, что происходит. Этот пример называется пазл грязные дети. Затем мы представим формализацию этой головоломки в логике, называемой Логика публичных объявлений (PAL). Загадка грязных детей - одна из самых известных головоломок, которая сыграла роль в развитии DEL. Другие важные загадки включают пазл суммы и произведения, то Дилемма Монти Холла, то Проблема с русскими картами, то проблема с двумя конвертами, Парадокс Мура, то парадокс палача, так далее.[24]
Пример Muddy Children:
У нас двое детей, А и Б, оба грязные. A может видеть B, но не себя, а B может видеть A, но не себя. Позволять - предложение о том, что A грязно, и быть утверждением, утверждающим, что B грязный.
- Представляем исходную ситуацию указанной эпистемической моделью представлен ниже, где отношения между мирами являются отношениями эквивалентности. состояния интуитивно представить возможные миры, предложение (например, ) выполнимый в одном из этих миров интуитивно означает, что в соответствующем возможном мире интуитивная интерпретация (A грязный) верно. Связи между мирами, помеченные агентами (A или B), интуитивно выражают понятие неразличимости для агента, о котором идет речь, между двумя возможными мирами. Например, связь между и помеченный A интуитивно означает, что A не может различить возможный мир из наоборот. Действительно, А не может видеть себя, поэтому он не может отличить мир, в котором он грязен, от мира, в котором он не грязен. Однако он может различать миры, в которых B является грязным или нет, потому что он может видеть B. Эта интуитивная интерпретация заставляет нас предположить, что наши отношения между мирами являются отношениями эквивалентности.
 Исходная ситуация: точечная эпистемическая модель
Исходная ситуация: точечная эпистемическая модель - Теперь предположим, что их отец приходит и объявляет, что хотя бы один грязный (формально ). Затем мы обновляем модель, и это дает указанную эпистемическую модель, представленную ниже. Что мы на самом деле делаем, так это подавляем миры, в которых содержание объявления не выполняется. В нашем случае это мир, в котором и верны. Это подавление и есть то, что мы называем обновлением. Затем мы получаем модель, изображенную ниже. В результате объявления и A, и B действительно знают, что по крайней мере один из них грязный. Мы можем прочитать это из эпистемической модели.
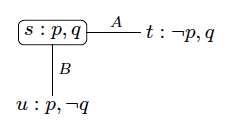 Обновленная эпистемическая модель после первого объявления
Обновленная эпистемическая модель после первого объявления - Теперь предположим, что есть второе (и последнее) объявление, в котором говорится, что ни один из них не знает, что он грязный (объявление может выражать факты о ситуации, а также эпистемологические факты о знаниях, которыми обладают агенты). Затем мы аналогичным образом обновляем модель, подавляя миры, которые не удовлетворяют содержанию объявления, или, что эквивалентно, оставляя миры, которые удовлетворяют объявлению. Таким образом, этот процесс обновления приводит к указанной ниже эпистемической модели. Интерпретируя эту модель, мы получаем, что A и B оба знают, что они грязные, что, похоже, противоречит содержанию объявления. Однако, если мы предположим, что A и B оба являются совершенными рассуждающими и что это общеизвестно среди них, тогда этот вывод имеет смысл.

Логика публичного объявления (PAL):
Мы представляем синтаксис и семантику Логика публичных объявлений (PAL), сочетающий в себе черты эпистемической логики и пропозициональная динамическая логика.[25]
Мы определяем язык индуктивно следующим грамматика в BNF:
куда .
Язык интерпретируется по эпистемическим моделям. В условия истины ибо связки эпистемического языка те же, что и в эпистемической логике (см. выше). Условие истинности для новой модальности динамического действия определяется следующим образом:
| если только |
куда с
,
для всех и
.
Формула интуитивно означает, что после правдивого объявления , держит. Публичное объявление предложения изменяет текущую эпистемическую модель, как показано на рисунке ниже.

Система доказательств определяется ниже звук и сильно полный за w.r.t. класс всех указанных эпистемических моделей.
| Аксиомы и правила вывода системы доказательств (см. выше) | ||
| Красный 1 | ||
| Красный 2 | ||
| Красный 3 | ||
| Красный 4 |
Аксиомы Red 1 - Red 4 называются редукционные аксиомы потому что они позволяют уменьшить любую формулу доказуемо эквивалентной формуле в . Формула это теорема доказуемо в . В нем говорится, что после публичного объявления , агент знает, что держит.
PAL - это разрешимый, это проблема проверки модели разрешима в полиномиальное время и это проблема выполнимости является PSPACE-полный.[26]
Пазл грязных детей, формализованный с помощью PAL:
Вот некоторые из утверждений, содержащихся в запутанной детской головоломке, формализованной в PAL.
«В исходной ситуации A грязный, а B грязный».
«В исходной ситуации A не знает, грязный ли он, а B - тоже».
«После публичного объявления о том, что по крайней мере один из детей A и B грязный, оба потом знают, что по крайней мере один из них грязный». Тем не мение:
«После публичного объявления о том, что по крайней мере один из детей A и B грязный, они все еще не знают, что они грязные». Более того:
«После последовательных публичных заявлений о том, что по крайней мере один из детей A и B грязный и что они все еще не знают, грязны ли они, A и B оба знают, что они грязные».
В этом последнем утверждении мы видим в действии интересную особенность процесса обновления: формула не обязательно верна после объявления. Это то, что мы технически называем «самостойкостью», и эта проблема возникает для эпистемических формул (в отличие от пропозициональных формул). Не следует путать объявление и обновление, вызванное этим объявлением, которое может отменить некоторую информацию, закодированную в объявлении.[27]
Произвольные события
В этом разделе мы предполагаем, что события не обязательно являются публичными, и сосредоточиваемся на пунктах 2 и 3 выше, а именно на том, как представлять события и как обновить эпистемическую модель с таким представлением событий посредством обновления продукта.
Модель событий
Эпистемические модели используются для моделирования того, как агенты воспринимают реальный мир. Их восприятие также можно описать с точки зрения знаний и убеждений о мире и верований других агентов. Суть подхода DEL состоит в том, что можно описать, как событие воспринимается агентами, очень похожим образом. Действительно, восприятие события агентами также может быть описано с точки зрения знаний и убеждений. Например, частное объявление к То, что ее карта красная, также можно описать с точки зрения знаний и убеждений: говорит что ее карта красная (событие ) верит что ничего не происходит (событие ). Это приводит к определению понятия модели событий, определение которой очень похоже на определение эпистемической модели.
Модель заостренных событий представляет, как фактическое событие представлено воспринимается агентами. Интуитивно означает, что пока возможное событие, представленное происходит, агент считает возможным, что возможное событие, представленное действительно происходит.
An модель событий кортеж куда:
- непустой набор возможные события,
- это бинарное отношение, называемое отношение доступности на , для каждого ,
- функция, называемая функция предусловия присвоение каждому возможному событию формулы .
обозначает множество .Мы пишем за , и называется модель заостренных событий ( часто представляет собой реальное событие).
Пример карты:
Вернемся к примеру с картой и предположим, что игроки и покажите свои карты друг другу. Как выясняется из, заметил это показала свою карту но не заметил что сделал это . Игроки и знаю это. Это событие представлено ниже в модели событий. .
Возможное событие соответствует фактическому событию «игроки и показать свои карты и карты соответственно друг другу »(с предварительным условием ), обозначает событие «игрок показывает свою грин-карту »(с предварительным условием ) и обозначает атомное событие "игрок" показывает свою красную карточку »(с предварительным условием ). Игроки и показать свои карты друг другу, игроки и знать это и считать возможным, пока игрок считает возможным, что игрок показывает свою красную карточку и также считает возможным, что игрок показывает свою грин-карту, так как не знает ее карты. Фактически, это все, что игрок считает возможным, потому что она не заметила, что показал свою карточку.

Другой пример модели событий приведен ниже. Этот второй пример соответствует событию, когда Player всем публично показывает свою красную карточку. Игрок показывает свою красную карточку, игроки , и "Знать" это, игроки , и «Знать», что каждый из них «знает» это, и Т. Д. Другими словами, есть всем известный факт среди игроков , и этот игрок показывает свою красную карточку.

Обновление продукта
Обновление продукта DEL описано ниже.[5] Это обновление дает новую точную эпистемическую модель представляя, как новая ситуация, которая ранее была представлена воспринимается агентами после наступления события, представленного .
Позволять быть эпистемической моделью и позволить быть моделью событий. В обновление продукта из и эпистемическая модель определяется следующим образом: для всех и все ,
| = | ||
| = | ||
| = |
Если и такие, что тогда обозначает заостренную эпистемическую модель . Это определение обновления продукта концептуально обосновано.[6]
Пример карты:
В результате первого события, описанного выше (Игроки и показать свои карты друг другу перед игроком ) агенты обновляют свои убеждения. Мы получаем ситуацию, представленную в указанной эпистемической модели ниже. В этой острой эпистемической модели справедливо следующее утверждение: В нем говорится, что игрок знает этого игрока есть карта, но игрок «считает», что это не так.

Результат второго события представлен ниже. В этой острой эпистемической модели справедливо следующее утверждение: . В нем говорится, что среди и что они знают истинное состояние мира (а именно имеет красную карточку, имеет грин-карту и имеет синюю карту), но не знает этого.

Основываясь на этих трех компонентах (эпистемическая модель, модель событий и обновление продукта), Балтаг, Мосс и Солецки определили общий логический язык, вдохновленный логическим языком пропозициональная динамическая логика[25] рассуждать об изменении информации и знаний.[5][6]
Смотрите также
Примечания
- ^ Plaza, янв (2007-07-26). «Логика публичных коммуникаций». Синтез. 158 (2): 165–179. Дои:10.1007 / s11229-007-9168-7. ISSN 0039-7857.
- ^ Гербранди, Джелле; Греневельд, Виллем (1 апреля 1997 г.). «Рассуждения об изменении информации». Журнал логики, языка и информации. 6 (2): 147–169. Дои:10.1023 / А: 1008222603071. ISSN 0925-8531.
- ^ Велтман, Франк (1996-06-01). «Значения по умолчанию в семантике обновления». Журнал философской логики. 25 (3): 221–261. CiteSeerX 10.1.1.77.9349. Дои:10.1007 / BF00248150. ISSN 0022-3611.
- ^ Дитмарш, Ханс П. ван (01.06.2002). «Описание действий в игре». Журнал логики, языка и информации. 11 (3): 349–365. Дои:10.1023 / А: 1015590229647. ISSN 0925-8531.
- ^ а б c Александру Балтаг; Лоуренс С. Мосс; Славомир Солецкий (1998). «Логика публичных заявлений и общеизвестных и частных подозрений». Теоретические аспекты рациональности и знания (TARK).
- ^ а б c Балтаг, Александру; Мосс, Лоуренс С. (2004-03-01). «Логика для эпистемических программ». Синтез. 139 (2): 165–224. Дои:10.1023 / B: SYNT.0000024912.56773.5e. ISSN 0039-7857.
- ^ Иногда проводится различие между событиями и действиями, причем действие представляет собой определенный тип события, выполняемого агентом.
- ^ Бох, Иван (1993). Эпистемическая логика в позднем средневековье. Рутледж. ISBN 978-0415057264.
- ^ Яако, Хинтикка (1962). Знание и вера, введение в логику двух понятий. Итака и Лондон: Издательство Корнельского университета. ISBN 978-1904987086.
- ^ а б Ленцен, Вольфганг (1978). «Последние работы в эпистемической логике». Acta Philosophica Fennica.
- ^ Баттигалли, Пьерпаоло; Бонанно, Джакомо (1999-06-01). «Последние результаты по убеждениям, знаниям и эпистемическим основам теории игр» (PDF). Исследования в области экономики. 53 (2): 149–225. Дои:10.1006 / reec.1999.0187. HDL:10419/189483.
- ^ а б Рональд Феджин; Джозеф Халперн; Йорам Моисей; Моше Варди (1995). Рассуждения о знаниях. MIT Press. ISBN 9780262562003.
- ^ Льюис, Дэвид (1969). Конвенция, философское исследование. Издательство Гарвардского университета. ISBN 978-0674170254.
- ^ Ауман, Роберт Дж. (1976-11-01). «Соглашаясь не соглашаться». Анналы статистики. 4 (6): 1236–1239. Дои:10.1214 / aos / 1176343654. JSTOR 2958591.
- ^ Патрик Блэкберн; Маартен де Рийке; Иде Венема (2001). Модальная логика. Издательство Кембриджского университета. ISBN 978-0521527149.
- ^ «Интернет-энциклопедия философии» Принцип К.К. (Знать, что знает) Интернет-энциклопедия философии »Печать». www.iep.utm.edu. Архивировано из оригинал на 2016-03-04. Получено 2015-12-11.
- ^ а б Например, предположим, что профессор университета считает (уверен), что один из семинаров ее коллеги состоится в четверг (формально ). На самом деле она ошибается, потому что сейчас вторник (). Поэтому она не знает, что семинар ее коллеги во вторник (). Если мы предположим, что аксиома верна, то мы должны сделать вывод, что она знает, что не знает, что семинар ее коллеги состоится во вторник () (и поэтому она тоже считает, что не знает этого: ). Это явно противоречит здравому смыслу.
- ^ а б Ленцен, Вольфганг (1979-03-01). "Epistemologische betrachtungen zu [S4, S5]". Erkenntnis (на немецком). 14 (1): 33–56. Дои:10.1007 / BF00205012. ISSN 0165-0106.
- ^ Ошер, Гийом (18 марта 2015 г.). «Сложные аксиомы как аксиомы взаимодействия» (PDF). Studia Logica. 103 (5): 1035–1062. Дои:10.1007 / s11225-015-9609-0. ISSN 0039-3215.
- ^ Стальнакер, Роберт (2006-03-01). «О логике познания и веры». Философские исследования. 128 (1): 169–199. Дои:10.1007 / s11098-005-4062-у. ISSN 0031-8116.
- ^ Флориди, Лучано (27 января 2011 г.). «Логика получения информации». Философия информации. Издательство Оксфордского университета. С. 224–243. Дои:10.1093 / acprof: oso / 9780199232383.003.0010. ISBN 9780191594809.
- ^ Halpern, Joseph Y .; Моисей, Йорам (1992). «Руководство по полноте и сложности модальной логики знания и веры». Искусственный интеллект. 54 (3): 319–379. Дои:10.1016/0004-3702(92)90049-4.
- ^ Халперн, Джозеф Ю. (1995-06-01). «Влияние ограничения количества примитивных предложений и глубины вложенности на сложность модальной логики». Искусственный интеллект. 75 (2): 361–372. Дои:10.1016 / 0004-3702 (95) 00018-А.
- ^ ван Дитмарш, Ганс; Куи, Бартельд (2015). Сто заключенных и лампочка - Springer. Дои:10.1007/978-3-319-16694-0. ISBN 978-3-319-16693-3.
- ^ а б Дэвид Харел; Декстер Козен; Ежи Тюрин (2000). Динамическая логика. MIT Press. ISBN 978-0262082891.
- ^ Лутц, Карстен (01.01.2006). Сложность и лаконичность логики публичного анонса. Труды Пятой международной совместной конференции по автономным агентам и многоагентным системам. AAMAS '06. Нью-Йорк, Нью-Йорк, США: ACM. С. 137–143. Дои:10.1145/1160633.1160657. ISBN 978-1-59593-303-4.
- ^ Дитмарш, Ханс Ван; Куи, Бартельд (01.07.2006). «Секрет моего успеха». Синтез. 151 (2): 201–232. Дои:10.1007 / s11229-005-3384-9. ISSN 0039-7857.
Рекомендации
- ван Бентем, Йохан (2011). Логическая динамика информации и взаимодействия. Издательство Кембриджского университета. ISBN 978-0521873970.
- Ханс, ван Дитмарш; Халперн, Джозеф; ван дер Хук, Вибе; Куи, Бартельд (2015). Справочник по эпистемической логике. Лондон: издание колледжа. ISBN 978-1848901582.
- ван Дитмарш, Ханс, ван дер Хук, Вибе и Коой, Бартельд (2007). Динамическая эпистемическая логика. Итака: том 337 библиотеки Synthese. Springer. ISBN 978-1-4020-5839-4.CS1 maint: несколько имен: список авторов (связь)
- Феджин, Рональд; Халперн, Джозеф; Моисей, Йорам; Варди, Моше (2003). Рассуждения о знаниях. Кембридж: MIT Press. ISBN 978-0-262-56200-3. Классическая справка.
- Хинтикка, Яакко (1962). Знание и вера - введение в логику двух понятий. Итака: Издательство Корнельского университета. ISBN 978-1-904987-08-6..
внешняя ссылка
- Балтаг, Александру; Ренне, Брайан. «Динамическая эпистемическая логика». В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии.
- ван Дитмарш, Ганс; ван дер Хук, Вибе; Куи, Бартельд. «Динамическая эпистемическая логика». Интернет-энциклопедия философии.
- Хендрикс, Винсент; Саймонс, Джон. «Эпистемическая логика». В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии.
- Гарсон, Джеймс. «Модальная логика». В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии.
























































































































































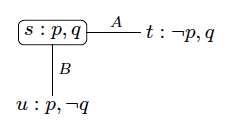

![{{ mathcal {L}} _ {PAL}}: phi ~~ :: = ~~ p ~ mid ~ neg phi ~ mid ~ ( phi land phi) ~ mid ~ K_ { j} phi ~ mid ~ [ phi!] phi](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3e5867b88382755e0f4d479fa6d017a8bb284c5)
![[ psi!] phi](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e2d92a45e41e6afc62a5e67bd24b4f27a42f133)
![{ Displaystyle { mathcal {M}}, ш модели [ psi!] phi}](https://wikimedia.org/api/rest_v1/media/math/render/svg/336da3ed0cd310a2f95561d6452e5e47e3fb6bee)







![[ psi!] p leftrightarrow ( psi rightarrow p)](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4e3c436287878941db025a86361369be1585682)
![[ psi!] neg phi leftrightarrow ( psi rightarrow neg [ psi!] phi)](https://wikimedia.org/api/rest_v1/media/math/render/svg/54a7df064b678ac79e736784ac2b980fec9f67a6)
![{ displaystyle [ psi!] ( phi land chi) leftrightarrow ([ psi!] phi land [ psi!] chi)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef7277529798e1134fd101f93db73f3546aeb4a7)
![[ psi!] K_ {i} phi leftrightarrow left ( psi rightarrow K_ {i} ( psi rightarrow [ psi!] phi) right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/89657a46761034cbe5573208d974b4e5233a5d3d)
![[q!] Kq](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8e62257ae1bfa879c0d8975290ba02a2b1a5316)


![{ displaystyle { mathcal {N}}, s models [p vee q!] (K_ {A} (p vee q) land K_ {B} (p vee q))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc4ada05c11376f8038aad786e0b6b79f49ae1dd)
![{ displaystyle { mathcal {N}}, s models [p vee q!] (( neg K_ {A} p land neg K_ {A} neg p) land ( neg K_ {B } q land neg K_ {B} neg q))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/663a38eba87041a860cbb227268988bd36d74a69)
![{ displaystyle { mathcal {N}}, s models [p vee q!] [( neg K_ {A} p land neg K_ {A} neg p) land ( neg K_ {B } q land neg K_ {B} neg q)!] (K_ {A} p land K_ {B} q)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c74909f6a8f28f02a243080149818b6c17823200)




































