Эллиптическая поверхность - Elliptic surface

В математика, эллиптическая поверхность является поверхностью, имеющей эллиптическое расслоение, другими словами правильный морфизм с подключенными волокнами к алгебраическая кривая такие, что почти все волокна гладкий кривые род 1. (Над алгебраически замкнутым полем, таким как комплексные числа, эти слои эллиптические кривые, возможно, без выбранного начала.) Это эквивалентно тому, что общий слой является гладкой кривой рода один. Это следует из правильное изменение базы.

Предполагается, что поверхность и базовая кривая неособые (комплексные многообразия или же регулярные схемы, в зависимости от контекста). Слои, не являющиеся эллиптическими кривыми, называются особые волокна и были классифицированы по Кунихико Кодайра. Как эллиптические, так и особые волокна важны в теория струн, особенно в F-теория.

Эллиптические поверхности образуют большой класс поверхностей, который содержит множество интересных примеров поверхностей и относительно хорошо изучен в теориях комплексных многообразий и гладкий 4-коллектор. Они подобны (имеют аналогию с, то есть) эллиптическим кривым над числовые поля.

Примеры

Произведение любой эллиптической кривой на любую кривую является эллиптической поверхностью (без особых слоев).
Все поверхности Кодаира измерение 1 - эллиптические поверхности.
Каждый комплекс Поверхность Энриквеса является эллиптическим и имеет эллиптическое расслоение над проективной прямой.
Поверхности Kodaira
Долгачевские поверхности
Модульные поверхности Shioda

Таблица особых волокон Кодаиры

Большинство слоев эллиптического расслоения представляют собой (неособые) эллиптические кривые. Остальные слои называются особыми слоями: их конечное число, и они состоят из объединений рациональных кривых, возможно, с особенностями или ненулевой кратностью (так что слои могут быть неприведенными схемами). Кодаира и Нерон независимо классифицировали возможные волокна и Алгоритм Тейта можно использовать, чтобы найти тип слоев эллиптической кривой над числовым полем.

В следующей таблице перечислены возможные волокна минимальный эллиптическое расслоение. («Минимальный» означает примерно тот, который нельзя разложить на «меньший»; точнее, особые слои не должны содержать гладких рациональных кривых с числом самопересечения -1.) Это дает:

Символ Кодаиры для волокна,
Андре Нерон символ волокна,
Количество неприводимых компонент слоя (все рациональные, кроме типа I₀)
Матрица пересечения компонентов. Это либо 1 × 1 нулевая матрица, или аффинная матрица Картана, чей Диаграмма Дынкина дано.
Кратности каждого слоя указаны на диаграмме Дынкина.

Кодаира	Нерон	Составные части	Матрица пересечения
я₀	А	1 (эллиптический)	0
я₁	B₁	1 (с двойной точкой)	0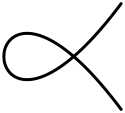
я₂	B₂	2 (2 различных точки пересечения)	аффинная A₁
я_v (v≥2)	B_v	v (v различных точек пересечения)	аффинная A_v-1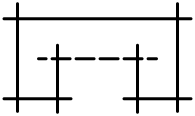
_мя_v (v≥0, м≥2)		я_v с множеством м
II	C₁	1 (с куспидом)	0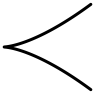
III	C₂	2 (встреча по порядку ведения заседания 2)	аффинная A₁
IV	C₃	3 (все сходятся в 1 очко)	аффинная A₂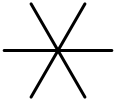
я₀^*	C₄	5	аффинный D₄
я_v^* (v≥1)	C_{5, в}	5 + v	аффинный D_{4 + v}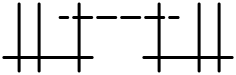
IV^*	C₆	7	аффинная E₆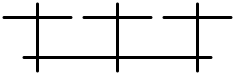
III^*	C₇	8	аффинная E₇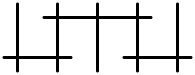
II^*	C₈	9	аффинная E₈

Эту таблицу можно найти следующим образом. Геометрические аргументы показывают, что матрица пересечения компонентов слоя должна быть отрицательно полуопределенной, связной, симметричной и не иметь диагональных элементов, равных −1 (по минимальности). Такая матрица должна быть 0 или кратной матрице Картана аффинной диаграммы Дынкина типа ADE.

Матрица пересечений определяет тип волокна за тремя исключениями:

Если матрица пересечений равна 0, волокно может быть либо эллиптической кривой (тип I₀) или иметь двойную точку (тип I₁) или куспид (тип II).
Если матрица пересечений аффинна A₁, есть 2 компоненты с кратностью пересечения 2. Они могут пересекаться либо в 2 точках с порядком 1 (тип I₂), или в одной точке с порядком 2 (тип III).
Если матрица пересечений аффинна A₂, есть 3 компонента, каждый из которых встречается с двумя другими. Они могут встречаться парами в 3 разных точках (тип I₃), либо все встречаются в одной точке (тип IV).

Монодромия

В монодромия вокруг каждого особого слоя есть хорошо определенная класс сопряженности в группе SL (2,Z) целочисленных матриц 2 × 2 с детерминант 1. Монодромия описывает способ, которым первые гомология группа гладкого слоя (изоморфная Z²) меняется при обходе особого слоя. Представители этих классов сопряженности, связанных с особыми слоями, задаются формулами:^[1]

Волокно	Матрица пересечения	Монодромия	j-инвариантный	Структура группы на гладком локусе
я_ν	аффинная A_ν-1	${ displaystyle { begin {pmatrix} 1 & nu 0 & 1 end {pmatrix}}}$	${ displaystyle infty}$	${ Displaystyle mathbf {Z} / nu times mathbf {C} ^ {*}}$
II	0	${ displaystyle { begin {pmatrix} 1 & 1 - 1 & 0 end {pmatrix}}}$	0	${ displaystyle mathbf {C}}$
III	аффинная A₁	${ displaystyle { begin {pmatrix} 0 & 1 - 1 & 0 end {pmatrix}}}$	1728	${ Displaystyle mathbf {Z} / 2 times mathbf {C}}$
IV	аффинная A₂	${ displaystyle { begin {pmatrix} 0 & 1 - 1 & -1 end {pmatrix}}}$	0	${ displaystyle mathbf {Z} / 3 times mathbf {C}}$
я_ν^*	аффинный D_{4 + ν}	${ displaystyle { begin {pmatrix} -1 & - nu 0 & -1 end {pmatrix}}}$	${ displaystyle infty}$	${ Displaystyle ( mathbf {Z} / 2) ^ {2} times mathbf {C}}$ если ν четно, ${ displaystyle mathbf {Z} / 4 times mathbf {C}}$ если ν нечетное
IV^*	аффинная E₆	${ displaystyle { begin {pmatrix} -1 & -1 1 & 0 end {pmatrix}}}$	0	${ displaystyle mathbf {Z} / 3 times mathbf {C}}$
III^*	аффинная E₇	${ displaystyle { begin {pmatrix} 0 & -1 1 & 0 end {pmatrix}}}$	1728	${ Displaystyle mathbf {Z} / 2 times mathbf {C}}$
II^*	аффинная E₈	${ displaystyle { begin {pmatrix} 0 & -1 1 & 1 end {pmatrix}}}$	0	${ displaystyle mathbf {C}}$

Для единичных волокон типа II, III, IV, IV^*, III^*, или II^*, монодромия имеет конечный порядок в SL (2,Z). Это отражает тот факт, что эллиптическое расслоение имеет потенциально хорошее сокращение у такого волокна. То есть после разветвленного конечного покрытия базовой кривой особый слой можно заменить гладкой эллиптической кривой. Какая гладкая кривая появляется, описывается j-инвариантный в таблице. Над комплексными числами кривая с j-инвариант 0 - единственная эллиптическая кривая с группой автоморфизмов порядка 6, а кривая с j-инвариант 1728 - единственная эллиптическая кривая с группой автоморфизмов порядка 4. (Все остальные эллиптические кривые имеют группу автоморфизмов порядка 2.)

Для эллиптического расслоения с раздел, называется Якобиево эллиптическое расслоение, гладкое геометрическое место каждого слоя имеет групповую структуру. Для сингулярных слоев эта групповая структура на гладком геометрическом месте описана в таблице, для удобства предполагается, что базовым полем являются комплексные числа. (Для особого слоя с матрицей пересечений, заданной аффинной диаграммой Дынкина ${ displaystyle { tilde { Gamma}}}$ , группа компонент гладкого множества изоморфна центру односвязной простой группы Ли с диаграммой Дынкина ${ displaystyle Gamma}$ , как указано здесь.) Знание групповой структуры особых слоев полезно для вычисления Группа Морделла-Вейля эллиптического расслоения (группы сечений), в частности его торсионной подгруппы.

Логарифмические преобразования

А логарифмическое преобразование (порядка м с центром п) эллиптической поверхности или расслоения поворачивает слой кратности 1 над точкой п базового пространства в слой кратности м. Его можно перевернуть, так что все волокна с высокой кратностью можно превратить в волокна с кратностью 1, и это можно использовать для устранения всех нескольких волокон.

Логарифмические преобразования могут быть довольно резкими: они могут изменить размерность Кодаиры и могут превратить алгебраические поверхности в неалгебраические поверхности.

Пример:Позволять L быть решеткой Z+ яZ из C, и разреши E быть эллиптической кривой C/L. Тогда карта проекции из E×C к C является эллиптическим расслоением. Мы покажем, как заменить слой над 0 слоем кратности 2.

Есть автоморфизм E×C порядка 2, отображающий (c,s) к (c+1/2, −s). Мы позволяем Икс быть частным от E×C этим групповым действием. Мы делаем Икс в волоконное пространство над C отображением (c,s) к s². Строим изоморфизм из Икс минус волокна от 0 до E×C минус слой над 0 отображением (c,s) к (c-бревно(s) / 2πi,s²). (Два слоя над 0 являются неизоморфными эллиптическими кривыми, поэтому расслоение Икс конечно не изоморфно расслоению E×C по всему C.)

Тогда расслоение Икс имеет слой кратности 2 над 0, а в остальном выглядит как E×C. Мы говорим что Икс получается применением логарифмического преобразования порядка 2 к E×C с центром 0.

Смотрите также

Примечания

^ Барт, Хулек, Питерс и Ван де Вен, Компактные сложные поверхности, раздел V.10, таблицы 5 и 6; Коссек и Долгачев, Энрикес Поверхности, Следствие 5.2.3.