Принцип свободной энергии - Free energy principle

В принцип свободной энергии это формальное заявление, объясняющее, как живые и неживые системы остаются в неравновесные стационарные состояния ограничивая себя ограниченным числом состояний.^[1] Он устанавливает, что системы минимизируют функцию свободной энергии своих внутренних состояний, что влечет за собой представления о скрытых состояниях в их среде. Неявная минимизация свободная энергия формально относится к вариационные байесовские методы и был первоначально представлен Карл Фристон как объяснение воплощенного восприятия в нейробиология,^[2] где он также известен как активный вывод.

Принцип свободной энергии объясняет существование данной системы, моделируя ее через Марковское одеяло который пытается минимизировать разницу между их моделью мира и их смысл и связанные восприятие. Это различие можно охарактеризовать как «неожиданность», и оно сводится к минимуму путем постоянной коррекции модели мира системы. Таким образом, этот принцип основан на байесовской идее мозга как «механизма вывода». Фристон добавил второй путь к минимизации: действие. Активно переводя мир в ожидаемое состояние, системы также могут минимизировать свободную энергию системы. Фристон считает, что это принцип всей биологической реакции.^[3] Фристон также считает, что его принцип применим к психические расстройства а также искусственный интеллект. Реализации AI, основанные на принципе активного вывода, показали преимущества перед другими методами.^[3]

Принцип свободной энергии подвергался критике за то, что его очень трудно понять даже специалистам.^[4] Обсуждения принципа также подвергались критике как метафизический предположения далеки от проверяемого научного предсказания, что делает принцип неопровержимым.^[5] В интервью 2018 года Фристон признал, что принцип свободной энергии неверен. фальсифицируемый: "принцип свободной энергии - это то, что он есть. принцип. Нравиться Принцип стационарного действия Гамильтона, это не может быть сфальсифицировано. Это невозможно опровергнуть. Фактически, вы мало что можете с этим поделать, если не спросите, соответствуют ли измеримые системы этому принципу ".^[6]

Фон

Представление о том, что самоорганизующийся биологические системы, такие как клетка или мозг, можно понимать как минимизацию вариационной свободной энергии, основанную на Гельмгольца Работа над бессознательный вывод^[7] и последующее лечение в психологии^[8] и машинное обучение.^[9] Вариативная свободная энергия - это функция наблюдений и плотности вероятности их скрытых причин. Этот вариационный Плотность определяется в связи с вероятностной моделью, которая генерирует предсказанные наблюдения по предполагаемым причинам. В этом случае свободная энергия приблизительно равна Доказательства байесовской модели.^[10] Следовательно, его минимизация может рассматриваться как процесс байесовского вывода. Когда система активно проводит наблюдения, чтобы минимизировать свободную энергию, она неявно выполняет активный вывод и максимизирует свидетельства своей модели мира.

Однако свободная энергия также является верхней границей самоинформация результатов, где долгосрочное среднее значение сюрприз энтропия. Это означает, что если система действует так, чтобы минимизировать свободную энергию, она неявно устанавливает верхнюю границу энтропии результатов - или сенсорных состояний - выборок.^{[11][12][нужен лучший источник ]}

Связь с другими теориями

Активный вывод тесно связан с теорема о хорошем регуляторе^[13] и связанные счета самоорганизация,^[14][15] Такие как самосборка, формирование рисунка, аутопоэзис^[16] и практика.^[17] В нем рассматриваются темы, рассмотренные в кибернетика, синергетика^[18] и воплощенное познание. Поскольку свободная энергия может быть выражена как ожидаемая энергия наблюдений при вариационной плотности за вычетом ее энтропии, она также связана с принцип максимальной энтропии.^[19] Наконец, поскольку среднее время энергии - это действие, принцип минимума вариационной свободной энергии принцип наименьшего действия.

Определение

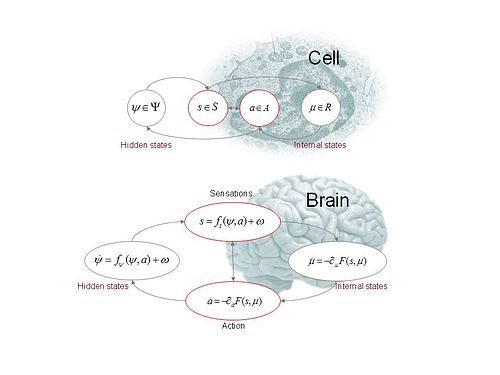
Определение (непрерывная формулировка): активный вывод опирается на кортеж ${ Displaystyle ( Omega, Psi, S, A, R, q, p)}$,

• Образец пространства ${ displaystyle Omega}$ - от чего случайные колебания ${ displaystyle omega in Omega}$ нарисованы
• Скрытые или внешние состояния ${ Displaystyle Psi: Psi times A times Omega to mathbb {R}}$ - которые вызывают сенсорные состояния и зависят от действий
• Сенсорные состояния ${ Displaystyle S: Psi times A times Omega to mathbb {R}}$ - вероятностное отображение действий и скрытых состояний
• Действие ${ displaystyle A: S times R to mathbb {R}}$ - это зависит от сенсорных и внутренних состояний
• Внутренние состояния ${ displaystyle R: R times S to mathbb {R}}$ - которые вызывают действие и зависят от сенсорных состояний
• Генеративная плотность ${ displaystyle p (s, psi mid m)}$ - над сенсорными и скрытыми состояниями в генеративной модели ${ displaystyle m}$
• Вариационная плотность ${ displaystyle q ( psi mid mu)}$ - по скрытым состояниям ${ Displaystyle psi in Psi}$ который параметризован внутренними состояниями ${ displaystyle mu in R}$

Действие и восприятие

Цель состоит в том, чтобы максимизировать модельные доказательства ${ displaystyle p (s mid m)}$ или минимизировать удивление ${ displaystyle - log p (s mid m)}$. Как правило, это связано с непреодолимой маргинализацией скрытых состояний, поэтому неожиданность заменяется верхней вариационной границей свободной энергии.^[9] Однако это означает, что внутренние состояния также должны минимизировать свободную энергию, потому что свободная энергия является функцией сенсорных и внутренних состояний:

${ displaystyle a (t) = { underset {a} { operatorname {arg , min}}} {F (s (t), mu (t)) }}$

${ displaystyle mu (t) = { underset { mu} { operatorname {arg , min}}} {F (s (t), mu)) }}$

${ displaystyle { underset { mathrm {free-energy}} { underbrace {F (s, mu)}}} = { underset { mathrm {energy}} { underbrace {E_ {q} [- log p (s, psi mid m)]}}} - { underset { mathrm {entropy}} { underbrace {H [q ( psi mid mu)]}}} = { underset { mathrm {неожиданность}} { underbrace {- log p (s mid m)}}} + { underset { mathrm {divergence}} { underbrace {D _ { mathrm {KL}} [q ( psi mid mu) parallel p ( psi mid s, m)]}}} geq { underset { mathrm {Surprise}} { underbrace {- log p (s mid m)} }}}$

Это вызывает двойную минимизацию действий и внутренних состояний, которые соответствуют действию и восприятию соответственно.

Минимизация бесплатной энергии

Минимизация бесплатной энергии и самоорганизация

Минимизация свободной энергии была предложена в качестве отличительной черты самоорганизующихся систем, если ее представить в виде случайные динамические системы.^[20] Эта формулировка опирается на Марковское одеяло (включающий действие и сенсорные состояния), разделяющий внутренние и внешние состояния. Если внутренние состояния и действие минимизируют свободную энергию, то они устанавливают верхнюю границу энтропии сенсорных состояний.

${ displaystyle lim _ {T to infty} { frac {1} {T}} { underset { text {free-action}} { underbrace { int _ {0} ^ {T} F (s (t), mu (t)) , dt}}} geq lim _ {T to infty} { frac {1} {T}} int _ {0} ^ {T} { underset { text {удивление}} { underbrace {- log p (s (t) mid m)}}} , dt = H [p (s mid m)]}$

Это потому что - под эргодический предположения - долгосрочное среднее значение неожиданности - это энтропия. Эта граница сопротивляется естественной тенденции к беспорядку, связанной с второй закон термодинамики и теорема о флуктуациях.

Минимизация свободной энергии и байесовский вывод

Все байесовские выводы можно сформулировать в терминах минимизации свободной энергии; например.,.^{[21][неудачная проверка ]} Когда свободная энергия минимизирована по отношению к внутренним состояниям, Дивергенция Кульбака – Лейблера между вариационной и апостериорной плотностью по скрытым состояниям сведена к минимуму. Это соответствует приблизительному Байесовский вывод - при фиксированной форме вариационной плотности - и точной Байесовский вывод иначе. Таким образом, минимизация свободной энергии обеспечивает общее описание байесовского вывода и фильтрации (например, Калмана фильтрация ). Он также используется в байесовском выбор модели, где свободная энергия может быть разложена на сложность и точность:

${ displaystyle { underset { text {free-energy}} { underbrace {F (s, mu)}}} = { underset { text {сложность}} { underbrace {D _ { mathrm {KL }} [q ( psi mid mu) parallel p ( psi mid m)]}}} - { underset { mathrm {precision}} { underbrace {E_ {q} [ log p ( s mid psi, м)]}}}}$

Модели с минимальной свободной энергией обеспечивают точное объяснение данных с учетом затрат на сложность (см. бритва Оккама и более формальные методы расчета вычислительных затрат^[22]). Здесь сложность - это расхождение между вариационной плотностью и предшествующими представлениями о скрытых состояниях (т. Е. Эффективными степенями свободы, используемыми для объяснения данных).

Минимизация свободной энергии и термодинамика

Вариационная свободная энергия - это теоретико-информационный функционал, отличный от термодинамической (Гельмгольца). свободная энергия.^[23] Однако термин сложности вариационной свободной энергии имеет ту же фиксированную точку, что и свободная энергия Гельмгольца (в предположении, что система термодинамически замкнута, но не изолирована). Это связано с тем, что, если сенсорные возмущения приостановлены (в течение достаточно длительного периода времени), сложность сводится к минимуму (поскольку точностью можно пренебречь). В этот момент система находится в равновесии, а внутренние состояния минимизируют свободную энергию Гельмгольца за счет принцип минимума энергии.^[24]

Минимизация свободной энергии и теория информации

Минимизация свободной энергии эквивалентна максимальному увеличению взаимная информация между сенсорными состояниями и внутренними состояниями, которые параметризуют вариационную плотность (для фиксированной вариационной плотности энтропии).^{[11][нужен лучший источник ]} Это связывает минимизацию свободной энергии с принципом минимального резервирования.^[25] и связанные методы лечения с использованием теории информации для описания оптимального поведения.^[26][27]

Минимизация свободной энергии в нейробиологии

Минимизация свободной энергии обеспечивает полезный способ сформулировать нормативные (оптимальные по Байесу) модели нейронного вывода и обучения в условиях неопределенности.^[28] и поэтому подписывается на Байесовский мозг гипотеза.^[29] Нейронные процессы, описываемые минимизацией свободной энергии, зависят от природы скрытых состояний: ${ Displaystyle Пси = Икс раз Тета раз Пи}$ которые могут включать в себя переменные, зависящие от времени, неизменные во времени параметры и точность (обратная дисперсия или температура) случайных флуктуаций. Минимизация переменных, параметров и точности соответствует выводу, обучению и кодированию неопределенности соответственно.

Перцептивный вывод и категоризация

Минимизация свободной энергии формализует понятие бессознательный вывод в восприятии^[7][9] и обеспечивает нормативную (байесовскую) теорию обработки нейронов. Теория связанных процессов нейрональной динамики основана на минимизации свободной энергии посредством градиентного спуска. Это соответствует обобщенная байесовская фильтрация (где ~ обозначает переменную в обобщенных координатах движения, а ${ displaystyle D}$ является производным матричным оператором):^[30]

${ displaystyle { dot { tilde { mu}}} = D { tilde { mu}} - partial _ { mu} F (s, mu) { Big |} _ { mu = { tilde { mu}}}}$

Обычно генеративные модели, определяющие свободную энергию, нелинейны и иерархичны (как корковые иерархии в головном мозге). Частные случаи обобщенной фильтрации включают: Калмана фильтрация, что формально эквивалентно прогнозирующее кодирование^[31] - популярная метафора передачи сообщений в мозгу. Согласно иерархическим моделям, прогнозирующее кодирование включает повторяющийся обмен восходящими (восходящими) ошибками предсказания и нисходящими (нисходящими) предсказаниями.^[32] что согласуется с анатомией и физиологией сенсорных^[33] и двигательные системы.^[34]

Восприятие обучения и памяти

При кодировании с предсказанием оптимизация параметров модели посредством возрастания градиента на временном интеграле свободной энергии (свободное действие) сводится к ассоциативному или Хеббийская пластичность и связан с синаптическая пластичность в мозгу.

Точность восприятия, внимание и заметность

Оптимизация параметров точности соответствует оптимизации усиления ошибок прогнозирования (сравните с усилением Калмана). В нейронально правдоподобных реализациях предсказательного кодирования^[32] это соответствует оптимизации возбудимости поверхностных пирамидных клеток и интерпретируется с точки зрения увеличения внимания.^[35]

Моделирование результатов, полученных с помощью задачи выборочного внимания, выполненной байесовской переформулировкой SAIM под названием PE-SAIM в среде с несколькими объектами. На графиках показана динамика активации FOA и двух шаблонных блоков в Knowledge Network.

Что касается противоречия «сверху вниз» и «снизу вверх», которое рассматривалось как серьезная открытая проблема внимания, вычислительная модель смогла проиллюстрировать циркуляционную природу взаимодействия между механизмами «сверху вниз» и «снизу вверх». Используя устоявшуюся модель эмерджентного внимания, а именно SAIM, авторы предложили модель PE-SAIM, которая в отличие от стандартной версии подходит к избирательному вниманию с позиции сверху вниз. Модель учитывает ошибки прогнозирования пересылки, отправленные на тот же уровень или на уровень выше, чтобы минимизировать функцию энергии, указывающую на разницу между данными и их причиной или, другими словами, между генеративной моделью и апостериорной. Чтобы повысить достоверность, они также включили в свою модель нейронную конкуренцию между стимулами. Примечательной особенностью этой модели является переформулировка функции свободной энергии только с точки зрения ошибок прогноза во время выполнения задачи.

${ displaystyle { dfrac { partial E ^ {total} (Y ^ {VP}, X ^ {SN}, x ^ {CN}, y ^ {KN})} { partial y_ {mn} ^ {SN }}} = x_ {mn} ^ {CN} -b ^ {CN} varepsilon _ {nm} ^ {CN} + b ^ {CN} sum _ {k} ( varepsilon _ {knm} ^ {KN })}$

куда, ${ displaystyle E ^ {total}}$ это общая функция энергии нейронных сетей влекут за собой, и ${ displaystyle varepsilon _ {knm} ^ {KN}}$ - ошибка прогноза между генеративной моделью (априорной) и апостериорной, изменяющейся во времени.^[36]Сравнение двух моделей показывает заметное сходство между их результатами, но при этом указывает на заметное несоответствие: в стандартной версии SAIM основное внимание уделяется возбуждающим связям, тогда как в PE-SAIM тормозные связи будут можно использовать для вывода. Модель также оказалась пригодной для прогнозирования данных ЭЭГ и фМРТ, взятых из экспериментов на людях, с высокой точностью. В том же духе Яхья и др. также применил принцип свободной энергии, чтобы предложить вычислительную модель для сопоставления шаблонов в скрытом избирательном визуальном внимании, которое в основном полагается на SAIM. ^[37]Согласно этому исследованию, полная свободная энергия всего пространства состояний достигается путем вставки нисходящих сигналов в исходные нейронные сети, посредством чего мы получаем динамическую систему, содержащую как прямую, так и обратную ошибку прогнозирования.

Активный вывод

Когда к действию применяется градиентный спуск ${ displaystyle { dot {a}} = - partial _ {a} F (s, { tilde { mu}})}$, моторный контроль можно понять в терминах классических рефлекторных дуг, которые задействованы нисходящими (кортикоспинальными) предсказаниями. Это обеспечивает формализм, обобщающий точечное решение равновесия на проблема степеней свободы^[38] - траекториям движения.

Активный вывод и оптимальный контроль

Активный вывод связан с оптимальный контроль путем замены функций стоимости или затрат на выполнение предыдущими представлениями о переходах между состояниями или потоке.^[39] Это использует тесную связь между байесовской фильтрацией и решением Уравнение беллмана. Однако активный вывод начинается с (априорного) потока ${ Displaystyle е = гамма cdot набла V + набла раз W}$ которые указаны с помощью скаляра ${ Displaystyle V (х)}$ и вектор ${ Displaystyle W (х)}$ ценностные функции пространства состояний (например, Разложение Гельмгольца ). Здесь, ${ displaystyle Gamma}$ - амплитуда случайных колебаний, а стоимость - ${ Displaystyle с (х) = е cdot nabla V + nabla cdot Gamma cdot V}$. Приоры переполнены ${ Displaystyle р ({ тильда {х}} середина м)}$ вызывать априорные состояния ${ Displaystyle р (х середина м) = ехр (V (х))}$ это решение подходящего форварда Уравнения Колмогорова.^[40] Напротив, оптимальное управление оптимизирует поток, учитывая функцию стоимости, в предположении, что ${ displaystyle W = 0}$ (т. е. поток не скручен или имеет детальный баланс). Обычно это влечет за собой решение обратного Уравнения Колмогорова.^[41]

Активный вывод и теория оптимальных решений (игры)

Оптимальное решение проблемы (обычно формулируемые как частично наблюдаемые марковские процессы принятия решений ) рассматриваются в рамках активного вывода путем поглощения служебные функции в предыдущие убеждения. В этом параметре состояния с высокой полезностью (низкой стоимостью) - это состояния, которые агент ожидает занять. Оснащая генеративную модель скрытыми состояниями, которые моделируют управление, политики (управляющие последовательности), минимизирующие вариационную свободную энергию, приводят к состояниям высокой полезности.^[42]

Нейробиологически нейромодуляторы, такие как дофамин Считается, что они сообщают о точности ошибок прогнозирования путем модуляции усиления ошибки прогнозирования кодирования основных ячеек.^[43] Это тесно связано, но формально отличается от роли дофамина в сообщении об ошибках прогнозирования. как таковой^[44] и связанные с ними вычислительные счета.^[45]

Активный вывод и когнитивная нейробиология

Активный вывод использовался для решения ряда проблем в когнитивная нейробиология, функция мозга и нейропсихиатрия, в том числе: наблюдение за действием,^[46] зеркальные нейроны,^[47] саккады и визуальный поиск,^[48][49] движения глаз,^[50] спать,^[51] иллюзии^[52] внимание,^[35] выбор действия,^[43] сознание,^[53][54] истерия^[55] и психоз.^[56] Объяснение действий в активном умозаключении часто зависит от идеи о том, что у мозга есть «устойчивые прогнозы», которые он не может обновить, что приводит к действиям, которые делают эти прогнозы реальностью.^[57]

Смотрите также

• Восприятие конкретного действия
• Доступность - Доступность - это возможность воздействия на объект или среду
• Автопоэзис - Системная концепция, предполагающая автоматическое воспроизведение и обслуживание
• Байесовские подходы к функции мозга
• Теория принятия решений
• Воплощенное познание
• Свободная энергия (значения)
• Инфо-метрики
• Оптимальный контроль
• Адаптивная система, также известный как Practopoiesis
• Предиктивное кодирование
• Практопоэз
• Самоорганизация - Процесс создания порядка посредством локальных взаимодействий
• Синергетика (Хакен)
• Вариационные байесовские методы

Рекомендации

внешняя ссылка

• Науки о поведении и мозге (Энди Кларк)