Геофизические исследования - Geophysical survey

Геофизические исследования систематический сбор геофизический данные для пространственных исследований. Обнаружение и анализ геофизических сигналов составляет основу обработки геофизических сигналов. Магнитные и гравитационные поля, исходящие из недр Земли, содержат важную информацию о сейсмической активности и внутренней структуре. Следовательно, очень важно обнаружение и анализ электрических и магнитных полей. Поскольку электромагнитные и гравитационные волны являются многомерными сигналами, все методы одномерного преобразования также могут быть расширены для анализа этих сигналов. Следовательно, в этой статье также обсуждаются методы многомерной обработки сигналов.

В геофизических исследованиях может использоваться большое количество разнообразных измерительных инструментов, а данные могут собираться сверху или снизу поверхности Земли или с воздушных, орбитальных или морских платформ. Геофизические исследования имеют множество приложений в геология, археология, разведка полезных ископаемых и энергетики, океанография, и инженерное дело. Геофизические исследования используются как в промышленности, так и в академических исследованиях.

Чувствительные инструменты, такие как гравиметр, датчик гравитационных волн и магнитометры обнаруживать колебания гравитационного и магнитного поля. Данные, собранные в результате геофизических исследований, анализируются, чтобы сделать из этого значимые выводы. Анализ спектральной плотности и частотно-временной локализации любого сигнала важен в таких приложениях, как разведка нефти и сейсмография.

Виды геофизических исследований

В геофизических исследованиях используется множество методов и типов инструментов. Технологии, используемые для геофизических исследований, включают:^[1]

1. Сейсмические методы, Такие как сейсмология отражений, сейсмическая рефракция, и сейсмическая томография. Этот тип исследования проводится для выявления подробной структуры скальных образований под поверхностью Земли.
2. Сейсмоэлектрический метод
3. Геодезия и методы гравитации, включая гравиметрия и гравитационная градиентометрия. Этот тип исследования проводится для выявления структуры скальных образований под поверхностью Земли.
4. Магнитные техники, включая аэромагнитные исследования и магнитометры.
5. Электротехника, включая томография электросопротивления, наведенная поляризация, спонтанный потенциал и морской источник управления электромагнитным (mCSEM) или ЭМ каротажа морского дна.^[2] Этот тип обследования проводится в основном для изучения наличия подземных вод.
6. Электромагнитные методы, Такие как магнитотеллурика, георадар и переходные процессы / электромагнетизм во временной области, поверхностный ядерный магнитный резонанс (также известное как магнитно-резонансное зондирование).^[3]
7. Скважинная геофизика, также называемая каротаж.
8. Методы дистанционного зондирования, включая гиперспектральный.

Обнаружение геофизических сигналов

В этом разделе рассматриваются принципы измерения геофизических волн. Магнитное и гравитационное поля являются важными компонентами геофизических сигналов.

Инструмент, используемый для измерения изменения гравитационного поля, - это гравиметр. Этот измеритель измеряет изменение силы тяжести из-за подземных образований и отложений. Для измерения изменений магнитного поля прибор магнитометр используется. Есть два типа магнитометров: один измеряет только вертикальную составляющую магнитного поля, а другой измеряет общее магнитное поле.

С помощью этих измерителей либо измеряются значения силы тяжести в разных местах, либо измеряются значения магнитного поля Земли. Затем в эти измеренные значения вносятся различные поправки и составляется карта аномалий. Анализируя эти карты аномалий, можно получить представление о структуре скальных образований в этой области. Для этого нужно использовать различные аналоговые или цифровые фильтры.

Измерение магнитных полей Земли

Магнитометры используются для измерения магнитных полей, магнитных аномалий на Земле. Чувствительность магнитометров зависит от требований. Например, вариации геомагнитных полей могут достигать нескольких aT, где 1aT = 10⁻¹⁸Т. В таких случаях специализированные магнитометры, такие как сверхпроводящее устройство квантовой интерференции (SQUID) используются.

Джим Циммерман был одним из разработчиков сверхпроводящего устройства квантовой интерференции ВЧ-диапазона (СКВИД) во время своей работы в исследовательской лаборатории Форда.^[4] Однако события, приведшие к изобретению СКВИДа, на самом деле были случайными. Джон Ламбе,^[4] во время своих экспериментов по ядерному магнитному резонансу заметил, что электрические свойства индий варьировались из-за изменения магнитного поля порядка нескольких нТл. Однако Ламбе не мог полностью понять полезность SQUID.

СКВИДы обладают способностью обнаруживать магнитные поля чрезвычайно низкой величины. Это связано с тем, что Джозефсоновский переход. Джим Циммерман был пионером в разработке SQUID, предложив новый подход к созданию джозефсоновских переходов. Он использовал ниобий провода и ленты ниобия, чтобы сформировать два джозефсоновских перехода, соединенных параллельно. Ленты действуют как прерывания сверхпроводящего тока, протекающего по проводам. Переходы очень чувствительны к магнитным полям и поэтому очень полезны при измерении полей порядка 10^{^-18}Т.

Измерение сейсмических волн с помощью датчика гравитационных волн

Датчики гравитационных волн могут обнаруживать даже мельчайшие изменения гравитационных полей из-за влияния более тяжелых тел. Большие сейсмические волны могут мешать гравитационным волнам и вызывать сдвиги в атомах. Следовательно, величину сейсмических волн можно определить по относительному смещению гравитационных волн.^[5]

Измерение сейсмических волн атомным интерферометром

На движение любой массы влияет гравитационное поле.^[6] На движение планет влияет огромное гравитационное поле Солнца. Точно так же более тяжелый объект будет влиять на движение других объектов меньшей массы, находящихся поблизости. Однако это изменение движения очень мало по сравнению с движением небесных тел. Следовательно, для измерения такого минутного изменения требуются специальные инструменты.

Описывает принцип атомного интерферометра.

Атомные интерферометры работать по принципу дифракция. В дифракционные решетки представляют собой наноматериалы с разделением четверти длины волны света. Когда пучок атомов проходит через дифракционную решетку, из-за собственной волновой природы атомов они расщепляются и образуют интерференционные полосы на экране. Атомный интерферометр очень чувствителен к изменениям положения атомов. По мере того как более тяжелые объекты меняют положение атомов поблизости, смещение атомов может быть измерено путем обнаружения сдвига интерференционных полос.

Существующие подходы к распознаванию геофизических сигналов

В этом разделе рассматриваются методы и математические методы распознавания сигналов и анализа сигналов. Он учитывает анализ сигналов во временной и частотной областях. В этом разделе также обсуждаются различные преобразования и их полезность при анализе многомерных волн.

3D выборка

Отбор проб

Первым шагом в любом подходе к обработке сигналов является аналого-цифровое преобразование. Геофизические сигналы в аналоговой области должны быть преобразованы в цифровую область для дальнейшей обработки. Большинство фильтров доступны как в 1D, так и в 2D.

Аналого-цифровое преобразование

Как следует из названия, гравитационные и электромагнитные волны в аналоговой области обнаруживаются, собираются и сохраняются для дальнейшего анализа. Сигналы могут быть дискретизированы как во временной, так и в частотной областях. Компонент сигнала измеряется как во времени, так и в пространстве. Например, выборка во временной области относится к измерению компонента сигнала в несколько моментов времени. Точно так же пространственная выборка относится к измерению сигнала в разных точках пространства.

Традиционная выборка одномерных сигналов, изменяющихся во времени, осуществляется путем измерения амплитуды рассматриваемого сигнала в дискретных интервалах времени. Аналогичным образом выборка пространственно-временных сигналов (сигналов, которые являются функциями четырех переменных - трехмерного пространства и времени) выполняется путем измерения амплитуды сигналов в разные моменты времени и в разных местах в пространстве. Например, гравитационные данные Земли измеряются с помощью датчик гравитационных волн или градиентометр^[7] поместив его в разные места в разные моменты времени.

Спектральный анализ

Многомерное преобразование Фурье

Разложение Фурье сигнала во временной области - это представление сигнала в виде суммы его частотных компонентов, в частности суммы синусов и косинусов. Жозеф Фурье придумал представление Фурье для оценки распределения тепла в теле. Тот же подход можно использовать для анализа многомерных сигналов, таких как гравитационные и электромагнитные волны.

4D Фурье-представление таких сигналов дается формулой

${displaystyle S (K, omega) = iint s (x, t) e ^ {- j (omega t-k'x)}, dx, dt}$

• ω представляет временную частоту и k представляет пространственную частоту.
• s(Икс,т) представляет собой 4-мерный пространственно-временной сигнал, который можно представить как бегущие плоские волны. Для таких плоских волн плоскость распространения перпендикулярна направлению распространения рассматриваемой волны.^[8]

Вейвлет-преобразование

Мотивом для разработки вейвлет-преобразования было кратковременное преобразование Фурье. Сигнал для анализа, скажем ж(т) умножается на оконную функцию ш(т) в определенный момент времени. Анализ коэффициентов Фурье этого сигнала дает нам информацию о частотных компонентах сигнала в определенный момент времени.^[9]

Математически STFT записывается как:

${displaystyle {x (t)} (au, omega) Equiv X (au, omega) = int _ {- infty} ^ {infty} x (t) w (t- au) e ^ {- jomega t}, dt }$

Вейвлет-преобразование определяется как

${displaystyle X (a, b) = {frac {1} {sqrt {a}}} int limits _ {} Psi ({frac {t-b} {a}}) x (t) dt}$

Для анализа можно использовать множество оконных функций. Вейвлет-функции используются как для временной, так и для частотной локализации. Например, одним из окон, используемых при вычислении коэффициентов Фурье, является окно Гаусса, которое оптимально сконцентрировано по времени и частоте. Этот оптимальный характер можно объяснить, рассматривая параметры масштабирования и сдвига по времени. а и б соответственно. Выбирая подходящие значения а и б, мы можем определить частоты и время, связанные с этим сигналом. Представляя любой сигнал как линейную комбинацию вейвлет-функций, мы можем локализовать сигналы как во временной, так и в частотной области. Следовательно, вейвлет-преобразования важны в геофизических приложениях, где важна пространственная и временная частотная локализация.^[10]

Частотно-временная локализация с помощью вейвлетов

Геофизические сигналы - это непрерывно меняющиеся функции пространства и времени. Методы вейвлет-преобразования предлагают способ разложить сигналы как линейную комбинацию сдвинутых и масштабированных версий базисных функций. Величину «сдвига» и «масштаба» можно изменить, чтобы локализовать сигнал по времени и частоте.

Формирование луча

Проще говоря, проблема фильтрации пространственно-временных сигналов^[11] можно рассматривать как определение скорости и направления определенного сигнала.^[12] При разработке фильтров для пространственно-временных сигналов используется тот же подход, что и для одномерных сигналов. Фильтры для одномерных сигналов спроектированы таким образом, что если требуется, чтобы фильтр извлекал частотные составляющие в определенном ненулевом диапазоне частот, полосовой фильтр с соответствующими частотами полосы пропускания и полосы заграждения. Точно так же в случае многомерных систем частотная характеристика фильтров рассчитывается таким образом, что она равна единице в расчетной области (k, ω) a.k.a. волновое число - частота и ноль в другом месте.^[12]

Пространственное распределение фазированных решеток для фильтрации геофизических сигналов

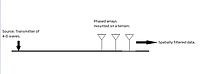
Этот подход применяется для фильтрации пространственно-временных сигналов.^[12] Он предназначен для изоляции сигналов, идущих в определенном направлении. Один из самых простых фильтров - это взвешенная задержка и суммирующий формирователь луча. Выход - это среднее значение линейной комбинации задержанных сигналов. Другими словами, выходной сигнал формирователя луча формируется путем усреднения взвешенных и задержанных версий сигналов приемника. Задержка выбирается так, чтобы полоса пропускания формирователя луча была направлена ​​в определенном направлении в пространстве.^[12]

Классическая теория оценивания

В этом разделе рассматривается оценка спектральной плотности мощности многомерных сигналов. Функцию спектральной плотности можно определить как многомерное преобразование Фурье автокорреляционной функции случайного сигнала.^[13]

${displaystyle Pleft (K_ {x}, wight) = int _ {- infty} ^ {infty} int _ {- infty} ^ {infty} varphi _ {ss} left (x, tight) e ^ {- jleft (wt -k'xight)}, dx, dt}$

${displaystyle varphi _ {ss} left (x, tight) = sleft [left (xi, au ight) s * left (xi -x, au -tight) ight]}$

Спектральные оценки могут быть получены путем нахождения квадрата величины преобразования Фурье, также называемого периодограммой. Спектральные оценки, полученные из периодограммы, имеют большой разброс по амплитуде для последовательных выборок периодограммы или по волновому числу. Эта проблема решается с помощью методов, составляющих классическую теорию оценивания. Вот они:

1. Бартлетт предложил метод усреднения спектральных оценок для расчета спектра мощности. Среднее значение спектральных оценок за интервал времени дает лучшую оценку.^[14]

${displaystyle P_ {B} left (wight) = {frac {1} {mathrm {det}, N}} sum _ {l} | sum _ {n} xleft (n + MIight) e ^ {- jleft (w ' ночь)} | ^ {2}}$ Дело Бартлетта ^[13]

2. Метод Велча предлагал разделить измерения с помощью функций окна данных, вычислить периодограмму, усреднить их, чтобы получить спектральную оценку, и рассчитать спектр мощности с помощью быстрого преобразования Фурье. Это увеличило скорость вычислений.^[15]

${displaystyle P_ {W} left (wight) = {frac {1} {mathrm {det}, N}} sum _ {l} | sum _ {n} gleft (ночь) xleft (n + MIight) e ^ {- jleft (w'night)} | ^ {2}}$ Дело Уэлча ^[13]

4. Рассматриваемую периодограмму можно модифицировать, умножив ее на оконную функцию. Окно сглаживания поможет нам сгладить оценку. Чем шире главный лепесток спектра сглаживания, тем плавнее он становится за счет частотного разрешения.^[13]

${displaystyle P_ {M} left (wight) = {frac {1} {detN}} | sum _ {n} gleft (ночь) xleft (ночь) e ^ {- jleft (w'night)} | ^ {2} }$ Модифицированная периодограмма ^[13]

Для получения дополнительной информации о спектральной оценке см. Спектральный анализ многомерных сигналов

Приложения

Оценка положения подземных объектов

Обсуждаемый здесь метод предполагает, что массовое распределение интересующих подземных объектов уже известно, и, следовательно, проблема оценки их местоположения сводится к параметрической локализации. Скажем, подземные объекты с центром масс (CM₁, СМ₂...СМ_п) расположены под поверхностью и в позициях p₁, п₂...п_п. Градиент силы тяжести (компоненты гравитационного поля) измеряется с помощью вращающегося колеса с акселерометрами, также называемого градиентометром силы тяжести.^[7] Инструмент расположен в разных ориентациях для измерения соответствующей составляющей гравитационного поля. Рассчитаны и проанализированы значения тензоров гравитационного градиента. Анализ включает наблюдение за вкладом каждого рассматриваемого объекта. Соблюдается процедура максимального правдоподобия и Граница Крамера – Рао (CRB) вычисляется для оценки качества оценки местоположения.

Обработка массивов для сейсмографических приложений

Различные датчики, расположенные на поверхности земли на равном расстоянии друг от друга, принимают сейсмические волны. Сейсмические волны проходят через различные слои земли и претерпевают изменения в своих свойствах - изменении амплитуды, времени прихода, фазовом сдвиге. Анализируя эти свойства сигналов, мы можем моделировать деятельность внутри Земли.

Визуализация 3D данных

Метод объемного рендеринга - важный инструмент для анализа скалярных полей. Объемный рендеринг упрощает представление трехмерного пространства. Каждая точка в трехмерном пространстве называется воксель. Данные внутри трехмерного набора данных проецируются на двумерное пространство (экран дисплея) с использованием различных методов. Существуют разные схемы кодирования данных для различных приложений, таких как МРТ, сейсмические приложения.

Рекомендации