Формат с плавающей запятой половинной точности - Half-precision floating-point format

Не путать с bfloat16, другой 16-битный формат с плавающей запятой.

В вычисление, половинная точность (иногда называют FP16) это двоичный плавающая точка формат номера компьютера что занимает 16 бит (два байта в современных компьютерах) в память компьютера.

Они могут выражать значения в диапазоне ± 65 504, при этом минимальное значение выше 1 составляет 1 + 1/1024.

в IEEE 754-2008 стандартный, 16-битный база-2 формат называется двоичный16. Он предназначен для хранения значений с плавающей запятой в приложениях, где более высокая точность не важна для выполнения арифметических вычислений.

Хотя реализации IEEE с плавающей запятой половинной точности относительно новы, существовало несколько более ранних 16-битных форматов с плавающей запятой, в том числе Hitachi HD61810 DSP.[1] 1982 года, WIF Скотта[2] и Графический процессор 3dfx Voodoo.[3]

Nvidia и Microsoft определил половина тип данных в Cg язык, выпущенный в начале 2002 года, и реализованный в кремнии в GeForce FX, выпущенный в конце 2002 года.[4] ILM искал формат изображения, который мог бы обрабатывать широкий динамический диапазон, но без жесткого диска и затрат памяти на представления с плавающей запятой, которые обычно используются для вычислений с плавающей запятой (одинарная и двойная точность).[5] Группа программируемого затенения с аппаратным ускорением во главе с Джоном Эйри в SGI (Кремниевая графика) изобрел тип данных s10e5 в 1997 году в рамках проекта «Бали». Это описано в СИГГРАФ Бумага 2000[6] (см. раздел 4.3) и дополнительно задокументировано в патенте США 7518615.[7]

Этот формат используется в нескольких компьютерная графика среды, включая MATLAB, OpenEXR, JPEG XR, GIMP, OpenGL, Cg, Direct3D, и D3DX. Преимущество перед 8-битными или 16-битными двоичными целыми числами заключается в том, что увеличенное динамический диапазон позволяет сохранить больше деталей в светлых участках и тени для изображений. Преимущество перед 32-битной одинарная точность бинарные форматы в том, что для них требуется половина памяти и пропускная способность (за счет точности и дальности).[5]

В F16C расширение позволяет процессорам x86 преобразовывать числа с плавающей запятой половинной точности в и из поплавки одинарной точности.

В зависимости от компьютера половинная точность может быть на порядок быстрее, чем двойная точность, например 37 PFLOPS против для половины 550 "AI-PFLOPS (Half Precision)".[8]

Плавающая точка форматы
IEEE 754
Другой

IEEE 754 двоичный формат с плавающей запятой половинной точности: binary16

Стандарт IEEE 754 определяет двоичный16 как имеющий следующий формат:

Формат выложен следующим образом:

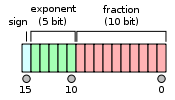
IEEE 754r Half Floating Point Format.svg

Предполагается, что формат имеет неявный ведущий бит со значением 1, если только поле экспоненты не хранится со всеми нулями. Таким образом, только 10 бит значимое появляются в формате памяти, но общая точность составляет 11 бит. В языке IEEE 754 имеется 10 значащих битов, но есть 11 битов значимой точности (log10(211) ≈ 3,311 десятичных цифр, или 4 цифры ± чуть меньше 5 единицы на последнем месте ).

Экспонентное кодирование

Двоичная экспонента с плавающей запятой половинной точности кодируется с использованием смещение-двоичный представление с нулевым смещением 15; также известный как смещение экспоненты в стандарте IEEE 754.

Таким образом, как определено двоичным представлением смещения, чтобы получить истинную экспоненту, смещение 15 должно быть вычтено из сохраненной экспоненты.

Сохраненные экспоненты 000002 и 111112 интерпретируются специально.

ЭкспонентаSignificand = нольЗначение ≠ нольУравнение
000002нуль, −0субнормальные числа(−1)знак × 2−14 × 0 значимых бит2
000012, ..., 111102нормализованное значение(−1)знак × 2показатель −15 × 1. Значащие биты2
111112±бесконечностьNaN (тихо, сигнализирует)

Минимальное строго положительное (субнормальное) значение равно 2−24 ≈ 5.96 × 10−8.Минимальное положительное нормальное значение - 2−14 ≈ 6.10 × 10−5Максимальное представимое значение - (2−2−10) × 215 = 65504.

Примеры половинной точности

Эти примеры даны в битовом представлении значения с плавающей запятой. Это включает знаковый бит, (смещенную) экспоненту и мантиссу.

0 00000 00000000012 = 000116 =  ≈ 0,000000059604645 (наименьшее положительное субнормальное число)
0 00000 11111111112 = 03ff16 =  ≈ 0,000060975552 (наибольшее субнормальное число)
0 00001 00000000002 = 040016 =  ≈ 0,000061035156 (наименьшее положительное нормальное число)
0 11110 11111111112 = 7bff16 =  = 65504 (наибольшее нормальное число)
0 01110 11111111112 = 3bff16 =  ≈ 0,99951172 (наибольшее число меньше единицы)
0 01111 00000000002 = 3c0016 =  = 1 (один)
0 01111 00000000012 = 3c0116 =  ≈ 1.00097656 (наименьшее число больше единицы)
0 01101 01010101012 = 355516 =  = 0,33325195 (округление от 1/3 до ближайшего)
1 10000 00000000002 = c00016 = −2
0 00000 00000000002 = 000016 = 01 00000 00000000002 = 800016 = −0
0 11111 00000000002 = 7c0016 = бесконечность1 11111 00000000002 = fc0016 = −infinity

По умолчанию 1/3 округления вниз, как для двойная точность, из-за нечетного количества бит в мантиссе. Таким образом, биты за точкой округления равны 0101... что меньше 1/2 единица на последнем месте.

Ограничения точности десятичных значений в [0, 1]

  • Десятичные числа от 2−24 (минимум положительный субнормальный) и 2−14 (максимальное субнормальное): фиксированный интервал 2−24
  • Десятичные числа от 2−14 (минимальная положительная норма) и 2−13: фиксированный интервал 2−24
  • Десятичные числа от 2−13 и 2−12: фиксированный интервал 2−23
  • Десятичные числа от 2−12 и 2−11: фиксированный интервал 2−22
  • Десятичные числа от 2−11 и 2−10: фиксированный интервал 2−21
  • Десятичные числа от 2−10 и 2−9: фиксированный интервал 2−20
  • Десятичные числа от 2−9 и 2−8: фиксированный интервал 2−19
  • Десятичные числа от 2−8 и 2−7: фиксированный интервал 2−18
  • Десятичные числа от 2−7 и 2−6: фиксированный интервал 2−17
  • Десятичные числа от 2−6 и 2−5: фиксированный интервал 2−16
  • Десятичные числа от 2−5 и 2−4: фиксированный интервал 2−15
  • Десятичные числа от 2−4 и 2−3: фиксированный интервал 2−14
  • Десятичные числа от 2−3 и 2−2: фиксированный интервал 2−13
  • Десятичные числа от 2−2 и 2−1: фиксированный интервал 2−12
  • Десятичные числа от 2−1 и 2−0: фиксированный интервал 2−11

Ограничения точности десятичных значений в [1, 2048]

  • Десятичные числа от 1 до 2: фиксированный интервал 2−10 (1+2−10 является следующим по величине числом с плавающей запятой после 1)
  • Десятичные числа от 2 до 4: фиксированный интервал 2−9
  • Десятичные числа от 4 до 8: фиксированный интервал 2−8
  • Десятичные числа от 8 до 16: фиксированный интервал 2−7
  • Десятичные числа от 16 до 32: фиксированный интервал 2−6
  • Десятичные числа от 32 до 64: фиксированный интервал 2−5
  • Десятичные числа от 64 до 128: фиксированный интервал 2−4
  • Десятичные числа от 128 до 256: фиксированный интервал 2−3
  • Десятичные числа от 256 до 512: фиксированный интервал 2−2
  • Десятичные числа от 512 до 1024: фиксированный интервал 2−1
  • Десятичные числа от 1024 до 2048: фиксированный интервал 20

Ограничения точности для целочисленных значений

  • Целые числа от 0 до 2048 могут быть точно представлены (а также между -2048 и 0)
  • Целые числа от 2048 до 4096 округляются до кратного 2 (четного числа)
  • Целые числа от 4096 до 8192 округляются до кратного 4
  • Целые числа от 8192 до 16384 округляются до кратного 8
  • Целые числа от 16384 до 32768 округляются до кратного 16
  • Целые числа от 32768 до 65519 округляются до кратного 32[9]
  • Целые числа выше 65519 округляются до «бесконечности» при использовании округления до четности, выше 65535 при использовании округления до нуля или выше 65504 при использовании округления до бесконечности.

Альтернативный вариант ARM с половинной точностью

Поддержка процессоров ARM (с плавающей точкой контрольный регистр bit) "альтернативный формат половинной точности", который устраняет особый случай для значения экспоненты 31 (111112).[10] Он почти идентичен формату IEEE, но в нем нет кодирования для бесконечности или NaN; вместо этого показатель степени 31 кодирует нормализованные числа в диапазоне от 65536 до 131008.

Использует

Аппаратное и программное обеспечение для машинное обучение или же нейронные сети как правило, используют половинную точность: такие приложения обычно выполняют большой объем вычислений, но не требуют высокого уровня точности.

На старых компьютерах, которые обращаются к 8 или 16 битам за раз (большинство современных компьютеров обращаются к 32 или 64 битам одновременно), арифметика половинной точности выполняется быстрее, чем одинарная точность, и значительно быстрее, чем двойная точность. В системах с инструкциями, которые могут обрабатывать несколько чисел с плавающей запятой в одной инструкции, половинная точность часто обеспечивает более высокую среднюю пропускную способность.[11]

Смотрите также

Рекомендации

  1. ^ "Hitachi :: dataBooks :: Руководство пользователя цифрового сигнального процессора HD61810". Archive.org. Получено 2017-07-14.
  2. ^ Скотт, Томас Дж. (Март 1991 г.). «Математика и информатика в разногласиях с действительными числами». SIGCSE '91 Материалы двадцать второго технического симпозиума SIGCSE по образованию в области компьютерных наук. 23 (1): 130–139. Дои:10.1145/107004.107029. ISBN  0897913779. S2CID  16648394.
  3. ^ "/home/usr/bk/glide/docs2.3.1/GLIDEPGM.DOC". Gamers.org. Получено 2017-07-14.
  4. ^ "vs_2_sw". Документация по Cg 3.1 Toolkit. Nvidia. Получено 17 августа 2016.
  5. ^ а б «OpenEXR». OpenEXR. Получено 2017-07-14.
  6. ^ Марк С. Пирси; Марк Олано; Джон Эйри; П. Джеффри Ангар. «Интерактивное многопроходное программируемое затенение» (PDF). People.csail.mit.edu. Получено 2017-07-14.
  7. ^ «Патент US7518615 - Система отображения с растеризацией с плавающей запятой и с плавающей запятой ... - Патенты Google». Google.com. Получено 2017-07-14.
  8. ^ «Об ABCI - О ABCI | ABCI». abci.ai. Получено 2019-10-06.
  9. ^ «Калькулятор поплавка Mediump». Получено 2016-07-26. Калькулятор половинной точности с плавающей запятой
  10. ^ "Поддержка чисел с плавающей запятой половинной точности". Руководство пользователя компилятора средств компиляции RealView. 10 декабря 2010 г.. Получено 2015-05-05.
  11. ^ Хо, Нхут-Минь; Вонг, Вен-Фай (1 сентября 2017 г.). «Использование арифметики половинной точности в графических процессорах Nvidia» (PDF). Департамент компьютерных наук, Национальный университет Сингапура. Получено 13 июля, 2020. Nvidia недавно представила встроенную поддержку операций с плавающей запятой половинной точности (FP16) в своих графических процессорах Pascal. В основном это было мотивировано возможностью того, что это ускорит работу приложений, интенсивно использующих данные и устойчивых к ошибкам, в графических процессорах.

дальнейшее чтение

внешняя ссылка