Горизонт - Horizon

А Высокая пустыня горизонт на закат солнца, Калифорния, СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ

В горизонт или линия горизонта очевидная линия, разделяющая Земля от небо, линия, разделяющая все видимые направления на две категории: те, которые пересекают поверхность Земли, и те, которые не пересекаются. истинный горизонт на самом деле теоретическая линия, которую можно наблюдать, только когда она лежит на поверхности моря. Во многих местах эта линия закрыта землей, деревьями, зданиями, горами и т. Д., И результирующее пересечение земли и неба называется пересечением земли и неба. видимый горизонт. Если смотреть на море с берега, то часть моря, ближайшая к горизонту, называется ближайший.^[1]

Истинный горизонт горизонтален. Он окружает наблюдателя, и обычно предполагается, что это круг, нарисованный на поверхности идеально сферической модели объекта. Земля. Его центр находится ниже наблюдателя и ниже уровень моря. Его расстояние от наблюдателя меняется день ото дня из-за атмосферная рефракция, на который сильно влияет Погода условия. Кроме того, чем выше глаза наблюдателя от уровня моря, тем дальше горизонт от наблюдателя. Например, в стандартные атмосферные условия для наблюдателя с уровнем глаз над уровнем моря на 1,70 метра (5 футов 7 дюймов) горизонт находится на расстоянии около 5 километров (3,1 мили).^[2]

При наблюдении с очень высоких точек зрения, таких как космическая станция, горизонт намного дальше и охватывает гораздо большую площадь поверхности Земли. В этом случае становится очевидным, что горизонт больше похож на эллипс, чем на идеальный круг, особенно когда наблюдатель находится выше экватора, и что поверхность Земли может быть лучше смоделирована как эллипсоид чем как сфера.

Этимология

Слово горизонт происходит от греческого "ὁρίζων κύκλος" Horizn Kyklos, "разделительный круг",^[3] где «ὁρίζων» происходит от глагола ὁρίζω горизонтō, "разделить", "разделить",^[4] что, в свою очередь, происходит от "ὅρος" (орос), «рубеж, ориентир».^[5]

Внешний вид и использование

Вид на океан с кораблем на горизонте (маленькая точка слева от корабля на переднем плане)

Исторически сложилось так, что расстояние до видимого горизонта долгое время было жизненно важным для выживания и успешной навигации, особенно в море, потому что оно определяло максимальную дальность обзора наблюдателя и, следовательно, общение, со всеми очевидными последствиями для безопасности и передачи информации, которые предполагал этот диапазон. Это значение уменьшилось с развитием радио и телеграф, но даже сегодня, летая на самолет под правила визуального полета, техника называется отношение летать используется для управления самолетом, при этом пилот использует визуальную связь между носом самолета и горизонтом для управления самолетом. Пилоты также могут сохранить свои ориентация в пространстве обращаясь к горизонту.

Во многих контекстах, особенно перспектива рисунок, кривизна Земля игнорируется, и горизонт считается теоретической линией, к которой горизонтальная плоскость сходятся (при проецировании на картинную плоскость) по мере увеличения расстояния от наблюдателя. Для наблюдателей рядом уровень моря разница между этим геометрический горизонт (что предполагает идеально ровную бесконечную поверхность земли) и истинный горизонт (что предполагает сферическая Земля поверхность) незаметна невооруженным глазом^{[сомнительный – обсудить]} (но для человека, находящегося на 1000-метровом холме с видом на море, истинный горизонт будет примерно на градус ниже горизонтальной линии).

В астрономии горизонт - это горизонтальная плоскость глазами наблюдателя. Это фундаментальная плоскость из горизонтальная система координат, геометрическое место точек, имеющих высота нулевых градусов. Хотя в некотором смысле он похож на геометрический горизонт, в этом контексте горизонт может рассматриваться как плоскость в пространстве, а не линия на картинной плоскости.

Расстояние до горизонта

Игнорирование эффект атмосферной рефракции, расстояние до истинного горизонта от наблюдателя, близкого к поверхности Земли, составляет около^[2]

{ displaystyle d приблизительно { sqrt {2 , h , R}} ,,}

где час высота выше уровень моря и р это Радиус Земли.

Когда d измеряется в километрах и час в метрах расстояние

{ displaystyle d приблизительно 3,57 { sqrt {h}} ,,}

где постоянная 3,57 имеет единицы км / м^½.

Когда d измеряется в милях (статутных милях, т. е. "сухопутных милях" 5 280 футов (1609 344 м)^[2]) и час в футах расстояние

{ displaystyle d приблизительно { sqrt {1.5h}} приблизительно 1.22 { sqrt {h}} ,.}

где постоянная 1,22 имеет единицы миль / фут^½.

В этом уравнении поверхность Земли предполагается идеально сферическим, причем р равняется примерно 6371 километру (3959 миль).

Примеры

Предполагая, что нет атмосферная рефракция и сферическая Земля с радиусом R = 6371 километр (3959 миль):

Для наблюдателя, стоящего на земле с час = 1,70 метра (5 футов 7 дюймов), горизонт находится на расстоянии 4,7 км (2,9 мили).
Для наблюдателя, стоящего на земле с час = 2 метра (6 футов 7 дюймов), горизонт находится на расстоянии 5 километров (3,1 мили).
Для наблюдателя, стоящего на холме или башне на высоте 30 метров (98 футов) над уровнем моря, горизонт находится на расстоянии 19,6 км (12,2 мили).
Для наблюдателя, стоящего на холме или башне на высоте 100 метров (330 футов) над уровнем моря, горизонт находится на расстоянии 36 километров (22 миль).
Для наблюдателя, стоящего на крыше Бурдж-Халифа, 828 метров (2717 футов) от земли и около 834 метра (2736 футов) над уровнем моря, горизонт находится на расстоянии 103 км (64 мили).
Для наблюдателя наверху гора Эверест (8 848 метров (29 029 футов) в высоту), горизонт находится на расстоянии 336 километров (209 миль).
Для U-2 пилот, летя на высоте 21 000 метров (69 000 футов), горизонт находится на расстоянии 521 километра (324 мили).

Другие планеты

На планетах земной группы и других твердых небесных телах с незначительными атмосферными эффектами расстояние до горизонта для «стандартного наблюдателя» изменяется как квадратный корень из радиуса планеты. Таким образом, горизонт на Меркурий находится на 62% дальше от наблюдателя, чем на Земле, на Марс этот показатель составляет 73%, на Луна этот показатель составляет 52%, на Мимас цифра 18% и так далее.

Вывод

Геометрическая основа для вычисления расстояния до горизонта, теорема о секущем касательном

Геометрическое расстояние до горизонта, теорема Пифагора

Три типа горизонта

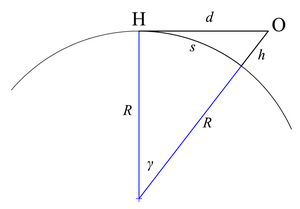
Если предположить, что Земля представляет собой безликую сферу (а не сплюснутый сфероид ) без атмосферной рефракции, то расстояние до горизонта можно легко вычислить.^[6]

В теорема о секущей и касательной утверждает, что

{ Displaystyle mathrm {OC} ^ {2} = mathrm {OA} times mathrm {OB} ,.}

Сделайте следующие замены:

d = OC = расстояние до горизонта
D = AB = диаметр Земли
час = OB = высота наблюдателя над уровнем моря
Д + ч = OA = диаметр Земли плюс высота наблюдателя над уровнем моря,

с участием д, д, и час все измерены в одних и тех же единицах. Формула теперь становится

{ Displaystyle d ^ {2} = час (D + час) , !}

или

{ displaystyle d = { sqrt {h (D + h)}} = { sqrt {h (2R + h)}} ,,}

где р это радиус Земли.

То же уравнение можно вывести с помощью теорема Пифагора На горизонте луч зрения проходит по касательной к Земле, а также перпендикулярно ее радиусу. В результате получается прямоугольный треугольник с суммой радиуса и высоты в качестве гипотенузы. С участием

d = расстояние до горизонта
час = высота наблюдателя над уровнем моря
р = радиус Земли

обращение ко второму рисунку справа приводит к следующему:

{ Displaystyle (R + H) ^ {2} = R ^ {2} + d ^ {2} , !}

{ Displaystyle R ^ {2} + 2Rh + h ^ {2} = R ^ {2} + d ^ {2} , !}

{ displaystyle d = { sqrt {h (2R + h)}} ,.}

Точная формула выше может быть расширена как:

{ displaystyle d = { sqrt {2Rh + h ^ {2}}} ,,}

где р - радиус Земли (р и час должны быть в тех же единицах). Например, если спутник находится на высоте 2000 км, расстояние до горизонта составляет 5430 километров (3370 миль); пренебрежение вторым членом в скобках даст расстояние 5048 километров (3137 миль), ошибка 7%.

Приближение

Графики расстояний до истинного горизонта на Земле для заданной высоты час. s по поверхности Земли, d - расстояние по прямой, а ~ d приблизительное расстояние по прямой в предположении час << радиус Земли 6371 км. В изображение SVG, наведите указатель мыши на график, чтобы выделить его.

Если наблюдатель находится близко к поверхности Земли, то можно пренебречь час в срок (2р + час), и формула принимает вид -

{ displaystyle d = { sqrt {2Rh}} ,.}

Используя километры для d и ри метры для час, и принимая радиус Земли равным 6371 км, расстояние до горизонта составляет

{ displaystyle d приблизительно { sqrt {2 cdot 6371 cdot {h / 1000}}} приблизительно 3.570 { sqrt {h}} ,}

.

С помощью имперские единицы, с участием d и р в статутные мили (как обычно используется на суше), и час в футах расстояние до горизонта составляет

{ displaystyle d приблизительно { sqrt {2 cdot 3963 cdot {h / 5280}}} приблизительно { sqrt {1.5h}} приблизительно 1,22 { sqrt {h}}}

.

Если d в морские мили, и час в футах постоянный коэффициент составляет около 1,06, что достаточно близко к 1, поэтому его часто игнорируют, давая:

{ displaystyle d приблизительно { sqrt {h}}}

Эти формулы могут использоваться, когда час намного меньше, чем радиус Земли (6371 км или 3959 миль), включая все виды с любых горных вершин, самолетов или высотных воздушных шаров. С указанными константами и метрическая, и британская формулы имеют точность с точностью до 1% (см. Следующий раздел, чтобы узнать, как добиться большей точности). час имеет значение в отношении р, как и большинство спутники, то приближение больше не действует, и требуется точная формула.

Прочие меры

Расстояние дуги

Другое отношение включает расстояние по дуге s вдоль дуга над искривленная поверхность Земли до горизонта; с участием γ в радианы,

{ Displaystyle s = R gamma ,;}

тогда

{ displaystyle cos gamma = cos { frac {s} {R}} = { frac {R} {R + h}} ,.}

Решение для s дает

{ displaystyle s = R cos ^ {- 1} { frac {R} {R + h}} ,.}

Расстояние s также может быть выражено через расстояние прямой видимости d; от второго рисунка справа,

{ displaystyle tan gamma = { frac {d} {R}} ,;}

заменяя γ и перестановка дает

{ displaystyle s = R tan ^ {- 1} { frac {d} {R}} ,.}

Расстояния d и s почти одинаковы, когда высота объекта незначительна по сравнению с радиусом (то есть час ≪ р).

Зенитный угол

Максимальный зенитный угол для наблюдателя в однородной сферической атмосфере

Когда наблюдатель находится в приподнятом положении, горизонт зенитный угол может быть больше 90 °. Максимальный видимый зенитный угол возникает, когда луч касается поверхности Земли; из треугольника OCG на рисунке справа,

{ displaystyle cos gamma = { frac {R} {R + h}}}

где ${ displaystyle h}$ высота наблюдателя над поверхностью и ${ displaystyle gamma}$ - угловой наклон горизонта. Это связано с зенитным углом горизонта. ${ displaystyle z}$ от:

{ displaystyle z = gamma +90 {} ^ { circ}}

Для неотрицательной высоты ${ displaystyle h}$ , угол ${ displaystyle z}$ всегда ≥ 90 °.

Объекты над горизонтом

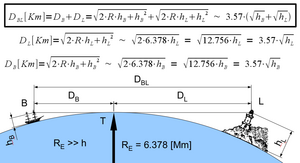
Расстояние до геометрического горизонта

Чтобы вычислить наибольшее расстояние, на котором наблюдатель может видеть верхнюю часть объекта над горизонтом, вычислите расстояние до горизонта для гипотетического наблюдателя, находящегося на вершине этого объекта, и добавьте его к расстоянию от реального наблюдателя до горизонта. Например, для наблюдателя ростом 1,70 м, стоящего на земле, горизонт находится на расстоянии 4,65 км. Для башни высотой 100 м расстояние до горизонта составляет 35,7 км. Таким образом, наблюдатель на пляже может видеть вершину башни, если она находится на расстоянии не более 40,35 км. И наоборот, если наблюдатель на лодке (час = 1,7 м) можно просто увидеть верхушки деревьев на ближайшем берегу (час = 10 м), деревья, вероятно, находятся примерно в 16 км.

Ссылаясь на рисунок справа, верхняя часть маяка будет видна наблюдателям в воронье гнездо на мачте лодки, если

{ displaystyle D _ { mathrm {BL}} <3.57 , ({ sqrt {h _ { mathrm {B}}}} + { sqrt {h _ { mathrm {L}}}}) ,,}

где D_BL находится в километрах и час_B и час_L в метрах.

Вид на залив шириной 20 км на побережье Испания. Обратите внимание кривизна Земли скрывая фундамент зданий на дальнем берегу.

В качестве другого примера предположим, что наблюдатель, чьи глаза находятся на высоте двух метров над уровнем земли, использует бинокль, чтобы посмотреть на удаленное здание, которое, как он знает, состоит из тридцати этажи высотой 3,5 метра каждая. Он считает, сколько этажей видит, и обнаруживает, что их всего десять. Так что двадцать этажей или 70 метров здания скрыты от него кривизной Земли. Отсюда он может рассчитать расстояние до здания:

{ displaystyle D приблизительно 3,57 ({ sqrt {2}} + { sqrt {70}})}

что составляет около 35 километров.

Аналогичным образом можно рассчитать, какая часть удаленного объекта видна над горизонтом. Предположим, что глаз наблюдателя находится на высоте 10 метров над уровнем моря, и он наблюдает за кораблем, находящимся на расстоянии 20 км. Его кругозор:

{ displaystyle 3.57 { sqrt {10}}}

километров от него, что составляет около 11,3 километров. Корабль находится еще в 8,7 км. Высота точки на корабле, которая видна наблюдателю, определяется как:

{ Displaystyle ч приблизительно влево ({ гидроразрыва {8.7} {3.57}} вправо) ^ {2}}

что составляет почти ровно шесть метров. Таким образом, наблюдатель может видеть ту часть корабля, которая находится более чем на шесть метров над уровнем воды. Та часть корабля, которая находится ниже этой высоты, скрыта от него кривизной Земли. В этой ситуации корабль считается разборка.

Эффект атмосферной рефракции

Из-за атмосферного преломление расстояние до видимого горизонта больше, чем расстояние, основанное на простом геометрическом расчете. Если поверхность земли (или воды) холоднее воздуха над ней, то близко к поверхности образуется холодный плотный слой воздуха, в результате чего свет преломляется вниз при движении и, следовательно, до некоторой степени распространяется вокруг поверхности. кривизна Земли. Обратное происходит, если земля горячее, чем воздух над ней, как это часто бывает в пустынях, производя миражи. В качестве приблизительной компенсации рефракции геодезисты, измеряющие расстояния более 100 метров, вычитают 14% из расчетной погрешности кривизны и гарантируют, что линия обзора находится на расстоянии не менее 1,5 метров от земли, чтобы уменьшить случайные ошибки, вызванные рефракцией.

Типичный пустынный горизонт

Если бы Земля была безвоздушным миром, как Луна, приведенные выше расчеты были бы точными. Однако у Земли есть атмосфера воздуха, чья плотность и показатель преломления значительно различаются в зависимости от температуры и давления. Это делает воздух преломлять свет в разной степени, влияя на внешний вид горизонта. Обычно плотность воздуха прямо над поверхностью Земли больше, чем его плотность на больших высотах. Это делает его показатель преломления больше у поверхности, чем на больших высотах, из-за чего свет, который движется примерно горизонтально, преломляется вниз.^[7] Это делает фактическое расстояние до горизонта больше, чем расстояние, рассчитанное по геометрическим формулам. При стандартных атмосферных условиях разница составляет около 8%. Это изменяет коэффициент 3,57 в метрических формулах, использованных выше, примерно до 3,86.^[2] Например, если наблюдатель стоит на берегу моря с глазами на высоте 1,70 м над уровнем моря, по приведенным простым геометрическим формулам над горизонтом должно быть 4,7 км. Фактически, атмосферная рефракция позволяет наблюдателю видеть на 300 метров дальше, перемещая истинный горизонт на 5 км от наблюдателя.

Эта поправка может применяться и часто применяется как довольно хорошее приближение, когда атмосферные условия близки к стандарт. В необычных условиях это приближение не работает. На рефракцию сильно влияют температурные градиенты, которые могут значительно меняться изо дня в день, особенно над водой. В крайних случаях, обычно весной, когда теплый воздух перекрывает холодную воду, преломление может позволить свету следовать за поверхностью Земли на сотни километров. Противоположные условия возникают, например, в пустынях, где поверхность очень горячая, поэтому горячий воздух с низкой плотностью находится ниже более холодного. Это заставляет свет преломляться вверх, вызывая мираж эффекты, которые делают концепцию горизонта несколько бессмысленной. Поэтому расчетные значения эффектов рефракции в необычных условиях являются приблизительными.^[2] Тем не менее были предприняты попытки вычислить их более точно, чем описанное выше простое приближение.

За пределами видимого диапазона длин волн преломление будет другим. Для радар (например, для длин волн от 300 до 3 мм, то есть частот от 1 до 100 ГГц) радиус Земли можно умножить на 4/3, чтобы получить эффективный радиус, что дает коэффициент 4,12 в метрической формуле, т.е. горизонт радара будет 15% за геометрический горизонт или на 7% за пределами визуального. Коэффициент 4/3 не является точным, поскольку в визуальном случае рефракция зависит от атмосферных условий.

Метод интеграции - Sweer

Если известен профиль плотности атмосферы, расстояние d до горизонта дается^[8]

{ displaystyle d = {{R} _ { text {E}}} left ( psi + delta right) ,,}

где р_E это радиус Земли, ψ это наклон горизонта и δ преломление горизонта. Падение определяется довольно просто из

{ displaystyle cos psi = { frac {{R} _ { text {E}} { mu} _ {0}} { left ({{R} _ { text {E}}} + h right) mu}} ,,}

где час высота наблюдателя над Землей, μ - показатель преломления воздуха на высоте наблюдателя, а μ₀ - показатель преломления воздуха у поверхности Земли.

Рефракция должна быть найдена интегрированием

{ displaystyle delta = - int _ {0} ^ {h} { tan phi { frac {{ text {d}} mu} { mu}}} ,,}

где ${ displaystyle phi , !}$ угол между лучом и линией, проходящей через центр Земли. Углы ψ и ${ displaystyle phi , !}$ связаны

{ displaystyle phi = 90 {} ^ { circ} - psi ,.}

Простой метод - Янг

Гораздо более простой подход, который дает по существу те же результаты, что и описанное выше приближение первого порядка, использует геометрическую модель, но использует радиус Р' = 7/6 р_E. Расстояние до горизонта тогда^[2]

{ displaystyle d = { sqrt {2R ^ { prime} h}} ,.}

Принимая радиус Земли равным 6371 км, с d в км и час в м,

{ displaystyle d приблизительно 3,86 { sqrt {h}} ,;}

с участием d в ми и час в футах,

{ displaystyle d приблизительно 1,32 { sqrt {h}} ,.}

Результаты метода Янга довольно близки к результатам метода Суэра и достаточно точны для многих целей.

Кривизна горизонта

Кривизну горизонта легко увидеть на этой фотографии 2008 г., сделанной с Космический шатл на высоте 226 км (140 миль).

С точки над поверхностью Земли горизонт слегка виднеется. выпуклый; это дуга окружности. Следующее формула выражает основные геометрические отношения между этой визуальной кривизной ${ displaystyle kappa}$ , высота ${ displaystyle h}$ , и радиус Земли ${ displaystyle R}$ :

{ displaystyle kappa = { sqrt { left (1 + { frac {h} {R}} right) ^ {2} -1}} }

Кривизна обратна кривизне угловой радиус в радианы. Кривизна 1,0 выглядит как круг с угловым радиусом 57,3 °, что соответствует высоте около 2640 км (1640 миль) над поверхностью Земли. На высоте 10 км (6,2 миль; 33000 футов) крейсерский высота типичного авиалайнера, математическая кривизна горизонта составляет около 0,056, такая же кривизна обода круга с радиусом 10 м, если смотреть с 56 см прямо над центром круга. Однако видимая кривизна меньше, чем из-за преломление света атмосферой и затемнение горизонта высокими слоями облаков, которые уменьшают высоту над видимой поверхностью.

Точки схода

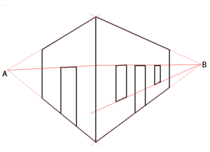
Две точки на горизонте находятся на пересечении линий, продолжающих сегменты, представляющие края здания на переднем плане. Линия горизонта здесь совпадает с линией наверху дверей и окон.

Горизонт - ключевая особенность картина самолет в науке о графическая перспектива. Предполагая, что плоскость изображения стоит вертикально к земле, и п перпендикулярная проекция точки глаза О на картинной плоскости горизонт определяется как горизонтальная линия, проходящая через п. Смысл п - точка схода перпендикулярных рисунку прямых. Если S это еще одна точка на горизонте, то это точка схода для всех линий параллельно к Операционные системы. Но Брук Тейлор (1719) указал, что плоскость горизонта определяется О и горизонт был как любой другой самолет:

Термин горизонтальная линия, например, склонен ограничивать представления учащегося до плоскости горизонта и заставлять его вообразить, что этот план пользуется некоторыми особыми привилегиями, которые делают фигуры в нем более легкими и удобными. быть описанным посредством этой Горизонтальной Линии, чем Фигуры в любой другой плоскости; ... Но в этой Книге я не делаю никакой разницы между Плоскостью Горизонта и любой другой Плоскостью вообще ...^[9]^[10]

Своеобразная геометрия перспективы, в которой параллельные линии сходятся на расстоянии, стимулировала развитие проективная геометрия который устанавливает точка в бесконечности где сходятся параллельные линии. В ее книге Геометрия искусства (2007), Кирсти Андерсен описал эволюцию перспективного рисования и науки до 1800 года, отметив, что точки схода не обязательно должны быть на горизонте. В главе "Горизонт" Джон Стиллвелл рассказал, как проективная геометрия привела к геометрия падения, современное абстрактное исследование пересечения линий. Стиллвелл также рискнул основы математики в разделе «Каковы законы алгебры?» «Алгебра точек», первоначально заданная Карл фон Штаудт вывод аксиом поле был деконструирован в двадцатом веке, открыв широкий спектр математических возможностей. Стиллвелл заявляет

Это открытие, сделанное 100 лет назад, кажется способным перевернуть математику с ног на голову, хотя математическое сообщество еще не полностью восприняло его. Это не только бросает вызов тенденции превращения геометрии в алгебру, но и предполагает, что и геометрия, и алгебра имеют более простую основу, чем считалось ранее.^[11]

Смотрите также

использованная литература

^ "Offing". Третий новый международный словарь Вебстера (Несокращенное ред.). Произносится «Хор-И-зон».
^ ^а ^б ^c ^d ^е ^ж Янг, Эндрю Т. «Расстояние до горизонта». Сайт Green Flash (разделы: Astronomical Refraction, Horizon Grouping). Факультет астрономии Государственного университета Сан-Диего. В архиве с оригинала 18 октября 2003 г.. Получено 16 апреля, 2011.
^ Лидделл, Генри Джордж и Скотт, Роберт. "ὁρίζων". Греко-английский лексикон. Цифровая библиотека Персея. В архиве из оригинала 5 июня 2011 г.. Получено 19 апреля, 2011.CS1 maint: использует параметр авторов (ссылка на сайт)
^ Лидделл, Генри Джордж и Скотт, Роберт. "ὁρίζω". Греко-английский лексикон. Цифровая библиотека Персея. В архиве из оригинала 5 июня 2011 г.. Получено 19 апреля, 2011.CS1 maint: использует параметр авторов (ссылка на сайт)
^ Лидделл, Генри Джордж и Скотт, Роберт. "ὅρος". Греко-английский лексикон. Цифровая библиотека Персея. В архиве из оригинала 5 июня 2011 г.. Получено 19 апреля, 2011.CS1 maint: использует параметр авторов (ссылка на сайт)
^ Плэйт, Фил (15 января 2009 г.). "Как далеко горизонт?". Обнаружить. Плохая астрономия. Kalmbach Publishing Co. В архиве из оригинала 29 марта 2017 г.. Получено 2017-03-28.
^ Проктор, Ричард Энтони; Раньярд, Артур Каупер (1892). Старая и новая астрономия. Longmans, Green and Company. стр.73.
^ Свир, Джон (1938). «Путь луча света, касающегося поверхности Земли». Журнал Оптического общества Америки. 28: 327–329. Bibcode:1938JOSA ... 28..327S. Дои:10.1364 / JOSA.28.000327.
^ Тейлор, Брук. Новые принципы перспективы. п. 1719.CS1 maint: использует параметр авторов (ссылка на сайт)
^ Андерсон, Кирсти (1991). "Работа Брука Тейлора о линейной перспективе". Springer. п. 151. ISBN 0-387-97486-5.
^ Стиллвелл, Джон (2006). «Тоска по невозможному». Горизонт. А. К. Петерс, ООО стр.47 –76. ISBN 1-56881-254-X.

дальнейшее чтение

Янг, Эндрю Т. "Падение горизонта". Сайт Green Flash (разделы: Astronomical Refraction, Horizon Grouping). Государственный университет Сан-Диего, факультет астрономии. Получено 16 апреля, 2011.

внешние ссылки

[WebstersThird-1] "Offing". Третий новый международный словарь Вебстера (Несокращенное ред.). Произносится «Хор-И-зон».

[ATYoungDistToHoriz-2] а ^б ^c ^d ^е ^ж Янг, Эндрю Т. «Расстояние до горизонта». Сайт Green Flash (разделы: Astronomical Refraction, Horizon Grouping). Факультет астрономии Государственного университета Сан-Диего. В архиве с оригинала 18 октября 2003 г.. Получено 16 апреля, 2011.

[3] Лидделл, Генри Джордж и Скотт, Роберт. "ὁρίζων". Греко-английский лексикон. Цифровая библиотека Персея. В архиве из оригинала 5 июня 2011 г.. Получено 19 апреля, 2011.CS1 maint: использует параметр авторов (ссылка на сайт)

[4] Лидделл, Генри Джордж и Скотт, Роберт. "ὁρίζω". Греко-английский лексикон. Цифровая библиотека Персея. В архиве из оригинала 5 июня 2011 г.. Получено 19 апреля, 2011.CS1 maint: использует параметр авторов (ссылка на сайт)

[5] Лидделл, Генри Джордж и Скотт, Роберт. "ὅρος". Греко-английский лексикон. Цифровая библиотека Персея. В архиве из оригинала 5 июня 2011 г.. Получено 19 апреля, 2011.CS1 maint: использует параметр авторов (ссылка на сайт)

[6] Плэйт, Фил (15 января 2009 г.). "Как далеко горизонт?". Обнаружить. Плохая астрономия. Kalmbach Publishing Co. В архиве из оригинала 29 марта 2017 г.. Получено 2017-03-28.

[ProctorRanyard1892-7] Проктор, Ричард Энтони; Раньярд, Артур Каупер (1892). Старая и новая астрономия. Longmans, Green and Company. стр.73.

[Sweer1938-8] Свир, Джон (1938). «Путь луча света, касающегося поверхности Земли». Журнал Оптического общества Америки. 28: 327–329. Bibcode:1938JOSA ... 28..327S. Дои:10.1364 / JOSA.28.000327.

[9] Тейлор, Брук. Новые принципы перспективы. п. 1719.CS1 maint: использует параметр авторов (ссылка на сайт)

[10] Андерсон, Кирсти (1991). "Работа Брука Тейлора о линейной перспективе". Springer. п. 151. ISBN 0-387-97486-5.

[11] Стиллвелл, Джон (2006). «Тоска по невозможному». Горизонт. А. К. Петерс, ООО стр.47 –76. ISBN 1-56881-254-X.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]