Монада (теория категорий) - Monad (category theory)
В теория категорий, филиал математика, а монада (также тройной, триада, стандартная конструкция и фундаментальная конструкция)[1] является эндофунктор (а функтор отображение категория себе) вместе с двумя естественные преобразования требуется для выполнения определенных условия согласованности. Монады используются в теории пар присоединенные функторы, и они обобщают операторы закрытия на частично упорядоченные наборы в произвольные категории.
Введение и определение
Монада - это определенный тип эндофунктор. Например, если и пара присоединенные функторы, с участием слева примыкает к , то композиция это монада. Если и являются обратными функторами, соответствующая монада функтор идентичности. В общем, добавок не эквивалентности - они связывают категории разной природы. Теория монад важна как часть попытки уловить то, что «сохраняют» присоединения. Другая половина теории, о том, что можно узнать также из рассмотрения , обсуждается в рамках дуальной теории комонады.
Формальное определение
В этой статье обозначает категория. А монада на состоит из эндофунктора вместе с двумя естественные преобразования: (где обозначает тождественный функтор на ) и (где это функтор от к ). Они необходимы для выполнения следующих условий (иногда называемых условия согласованности ):
- (как естественные преобразования );
- (как естественные преобразования ; Вот обозначает тождественное преобразование из к ).
Мы можем переписать эти условия, используя следующие коммутативные диаграммы:
 |  |
См. Статью о естественные преобразования для пояснения обозначений и , или посмотрите ниже коммутативные диаграммы, не использующие эти понятия:
 |  |
Первая аксиома сродни ассоциативность в моноиды если мы подумаем о как бинарную операцию моноида, а вторая аксиома сродни существованию элемент идентичности (который мы считаем заданным ). Действительно, монада на в качестве альтернативы можно определить как моноид в категории чьи объекты являются эндофункторами и чьи морфизмы являются естественными преобразованиями между ними, с моноидальная структура индуцируется составом эндофункторов.
Монада набора мощности
В мощность монада это монада по категории : Для набора позволять быть набор мощности из а для функции позволять - функция между наборами мощности, индуцированная взятием прямые изображения под . Для каждого набора , у нас есть карта , который присваивает каждому то одиночка . Функция
берет набор наборов в свой союз. Эти данные описывают монаду.
Замечания
Аксиомы монады формально аналогичны аксиомам моноид аксиомы. Фактически, монады являются частными случаями моноидов, а именно моноидами среди эндофункторы , который снабжен умножением на состав эндофункторов.
Состав монад - это вообще не монада. Например, монада двойного набора мощности не допускает монадной структуры. [2]
Комонады
В категоричный дуальный определение - это формальное определение комонада (или семейный); это можно быстро сказать в терминах, что комонада для категории это монада для противоположная категория . Следовательно, это функтор от себе, с набором аксиом для графство и коумножение которые возникают в результате переворота стрелок повсюду в только что данном определении.
Монады относятся к моноидам, как комонады для комоноиды. Каждый набор является комоноидом уникальным образом, поэтому комоноиды менее известны в абстрактная алгебра чем моноиды; однако комоноиды в категории векторных пространств с их обычным тензорным произведением важны и широко изучаются под названием коалгебры.
Терминологическая история
Понятие монады было изобретено Роджер Годеман в 1958 году под названием «Типовая конструкция». В 1960-х и 1970-х годах многие люди использовали название «тройка». Теперь стандартный термин «монада» возник из-за Saunders Mac Lane.
Примеры
Монады, возникающие из присоединений
Любые примыкание
рождает монаду на C. Эта очень распространенная конструкция работает следующим образом: эндофунктор - это композит.
Этот эндофунктор быстро рассматривается как монада, где карта юнитов происходит от карты юнитов. присоединения, а карта умножения строится с использованием карты конъюнкции присоединения:
Двойная дуализация
В монада двойной дуализации, для фиксированного поле k возникает из примыкания
где оба функтора задаются отправкой векторное пространство V к его двойное векторное пространство . Соответствующая монада отправляет векторное пространство V к его двойной двойной . Эта монада обсуждается в гораздо большей степени Кок (1970).
Операторы замыкания на частично упорядоченных множествах
Для категорий, возникающих из частично упорядоченные наборы (с единым морфизмом от к если только ), то формализм значительно упрощается: присоединенные пары Связи Галуа и монады операторы закрытия.
Свободно-забывчивые дополнения
Например, пусть быть забывчивый функтор от категория Grp из группы к категория Набор наборов, и пусть быть свободная группа функтор из категории множеств в категорию групп. потом примыкает к . В этом случае ассоциированная монада берет набор и возвращает базовый набор свободной группы Единичное отображение этой монады задается отображениями
включая любой набор в набор естественным образом, как строки длины 1. Далее, умножение этой монады есть отображение
сделан из натурального конкатенация или «сплющивание» «цепочек струн». Это составляет два естественные преобразования Предыдущий пример о свободных группах можно обобщить на любой тип алгебры в смысле разнообразие алгебр в универсальная алгебра. Таким образом, каждый такой тип алгебры порождает монаду в категории множеств. Важно отметить, что тип алгебры может быть восстановлен из монады (как категория алгебр Эйленберга – Мура), поэтому монады также можно рассматривать как обобщающие многообразия универсальных алгебр.
Другая монада, возникающая из присоединения, - это когда - эндофунктор в категории векторных пространств, отображающий векторное пространство к его тензорная алгебра , и который отображает линейные отображения в их тензорное произведение. Тогда у нас есть естественное преобразование, соответствующее вложению в его тензорная алгебра, и естественное преобразование, соответствующее отображению из к получается простым разложением всех тензорных произведений.
Монады кодовой плотности
В мягких условиях функторы, не допускающие левого сопряженного, также порождают монаду, так называемую монада кодовой плотности. Например, включение
не допускает левого сопряженного. Его монада кодовой плотности - это монада на наборах, отправляющих любой набор Икс к набору ультрафильтры на Икс. Этот и подобные примеры обсуждаются в Ленстер (2013).
Алгебры для монады
Учитывая монаду по категории , естественно считать -алгебры, т.е. объекты C действовал на Т способом, совместимым с единицей и умножением монады. Более формально Т-алгебра это объект из вместе со стрелкой из называется структурная карта алгебры такая, что диаграммы
 | и | 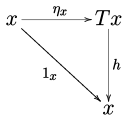 |
ездить.
Морфизм из -алгебры - это стрела из так что диаграмма

ездит на работу. Т-алгебры образуют категорию, называемую Категория Эйленберга – Мура и обозначается . Например, для свободной групповой монады, рассмотренной выше, a Т-алгебра - это набор Икс вместе с картой из свободной группы, сгенерированной Икс в направлении Икс при соблюдении условий ассоциативности и унитарности. Такая структура эквивалентна утверждению, что Икс это сама группа.
Другой пример - монада распределения по категории множеств. Определяется отправкой набора Икс к набору функций с конечной опорой и такой, что . Просматривая определения, можно показать, что алгебры над монадой распределения эквивалентны выпуклые множества, т.е. множества, снабженные операциями для подчиняется аксиомам, напоминающим поведение выпуклых линейных комбинаций в евклидовом пространстве.[3]
Монады и присоединения
Как было сказано выше, любое присоединение порождает монаду. И наоборот, каждая монада возникает из некоторого присоединения, а именно присоединения свободно-забывчивого
чей левый сопряженный посылает объект Икс бесплатно Т-алгебра Т(Икс). Тем не менее, обычно есть несколько различных добавлений, дающих начало монаде: let быть категорией, объекты которой являются дополнениями такой, что а стрелки - морфизмы присоединений, тождественных на . Тогда указанное выше присоединение свободно-забывчивости с использованием категории Эйленберга – Мура является конечным объектом в . Исходным объектом является Категория Клейсли, которая по определению является полной подкатегорией состоящий только из бесплатных Т-алгебры, т.е. Т-алгебры вида для какого-то объекта Икс из C.
Монадические присоединения
Учитывая любое присоединение с ассоциированной монадой Т, функтор г можно разложить на множители как
т.е. г(Y) естественно наделить Т-алгебра для любого Y в D. Примыкание называется монадическое присоединение если первый функтор дает эквивалентность категорий между D и категория Эйленберга – Мура .[4] По расширению, функтор как говорят монадический если у него есть сопряженный слева образуя монадическое присоединение. Например, соединение между группами и множествами со свободным забыванием является монадическим, поскольку алгебры над ассоциированной монадой являются группами, как упоминалось выше. В общем, знание того, что присоединение является монадическим, позволяет реконструировать объекты в D из предметов в C и Т-действие.
Теорема Бека монадичности
Теорема Бека монадичности дает необходимое и достаточное условие монадичности присоединения. Упрощенная версия этой теоремы утверждает, что г является монадическим, если это консервативный (или г отражает изоморфизмы, т.е. морфизм в D является изоморфизмом тогда и только тогда, когда его образ при г является изоморфизмом в C) и C имеет и г сохраняет соэквалайзеры.
Например, забывчивый функтор из категории компактный Хаусдорфовы пространства множествам монадичен. Однако функтор забывчивости из всех топологических пространств в множества не является консервативным, поскольку существуют непрерывные биективные отображения (между некомпактными или нехаусдорфовыми пространствами), которые не могут быть гомеоморфизмы. Таким образом, этот забывчивый функтор не монадический.[5]Двойственная версия теоремы Бека, характеризующая комонадические присоединения, актуальна в различных областях, таких как теория топоса и темы в алгебраическая геометрия относится к спуск. Первым примером комонадического присоединения является присоединение
для гомоморфизма колец между коммутативными кольцами. Это присоединение комонадично по теореме Бека тогда и только тогда, когда B является точно плоский как А-модуль. Таким образом, позволяет спускаться B-модули, снабженные нисходящим элементом данных (т.е. действием комонады, заданным присоединением) к А-модули. В результате теория точно ровный спуск широко применяется в алгебраической геометрии.
Использует
Монады используются в функциональное программирование для выражения типов последовательных вычислений (иногда с побочными эффектами). Увидеть монады в функциональном программировании, и более математически ориентированный модуль Wikibook б: Haskell / Теория категорий.
В категориальной логике проводится аналогия между теорией монад-комонад и модальная логика через операторы закрытия, внутренние алгебры, и их отношение к модели из S4 и интуиционистская логика.
Обобщение
Можно определить монады в 2 категории . Описанные выше монады - это монады для .
Смотрите также
- Распределительный закон между монадами
- Теория Ловера
- Монада (функциональное программирование)
- Поляда
- Сильная монада
использованная литература
- ^ Барр, Майкл; Уэллс, Чарльз (1985), «Топосы, тройки и теории» (PDF), Grundlehren der Mathematischen Wissenschaften, Springer-Verlag, 278, стр. 82 и 120, ISBN 0-387-96115-1.
- ^ Клин; Саламанка, Итерированный ковариантный набор степеней - это не монада, Дои:10.1016 / j.entcs.2018.11.013
- ^ Wirszcz, T. (1974), "Монадические функторы и выпуклость", Бык. Акад. Полон. Sci. Сэр. Sci. Математика. Астроном. Phys., 22: 39–42, Г-Н 0390019,Джейкобс, Барт (2010), «Выпуклость, двойственность и эффекты», Теоретическая информатика, Достижения ИФИП в области информационных и коммуникационных технологий, 323, стр. 1–19, Дои:10.1007/978-3-642-15240-5_1, ISBN 978-3-642-15239-9
- ^ Маклейн (1978) использует более сильное определение, в котором две категории изоморфны, а не эквивалентны.
- ^ Маклейн (1978, §§VI.3, VI.9)
дальнейшее чтение
- Барр, Майкл; Уэллс, Чарльз (1999), Теория категорий для вычислительной науки (PDF)
- Годеман, Роджер (1958), Topologie Algébrique et Théorie des Faisceaux., Actualités Sci. Ind., Publ. Математика. Univ. Страсбург, 1252, Paris: Hermann, стр. Viii + 283 с.
- Кок, Андерс (1970), "О монадах двойной дуализации", Mathematica Scandinavica, 27: 151, Дои:10.7146 / math.scand.a-10995
- Ленстер, Том (2013), "Плотность кодирования и монада ультрафильтров", Теория и приложения категорий, 28: 332–370, arXiv:1209.3606, Bibcode:2012arXiv1209.3606L
- Маклейн, Сондерс (1978), Категории для рабочего математика, Тексты для выпускников по математике, 5, Дои:10.1007/978-1-4757-4721-8, ISBN 978-1-4419-3123-8
- Педиккио, Мария Кристина; Толен, Уолтер, ред. (2004). Категориальные основания. Специальные разделы теории порядка, топологии, алгебры и пучков. Энциклопедия математики и ее приложений. 97. Кембридж: Издательство Кембриджского университета. ISBN 0-521-83414-7. Zbl 1034.18001.
- Риль, Эмили (2017), Теория категорий в контексте, ISBN 9780486820804
- Тури, Даниэле (1996–2001), Категория Теория Лекционные заметки (PDF)
внешние ссылки
- Монады, пять коротких лекций (с одним приложением).
- Джона Баэза Результаты этой недели по математической физике (неделя 89) охватывает монады в 2-х категориях.
































































![{ displaystyle f: X до [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbce99d737c06662e393d2d3dba7505a1e6c6eb6)


![{ Displaystyle г в [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d4a8acea9f5c4e59d8f5fd0ea3c695efa7252fe)












