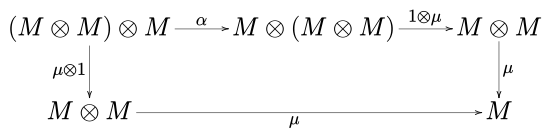Моноид (теория категорий) - Википедия - Monoid (category theory)
В теория категорий, филиал математика, а моноид (или же моноидный объект, или же внутренний моноид, или же алгебра) (M, μ, η) в моноидальная категория (C, ⊗, я) является объект M вместе с двумя морфизмы
- μ: M ⊗ M → M называется умножение,
- η: я → M называется единица измерения,
такой, что пятиугольник диаграмма
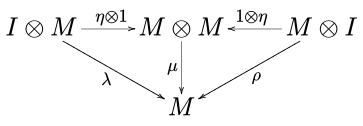
и диаграмма юнитора
ездить. В приведенных выше обозначениях я - единичный элемент, а α, λ и ρ - соответственно ассоциативность, левая и правая единицы моноидальной категории. C.
Вдвойне комоноид в моноидальной категории C моноид в двойная категория Cop.
Предположим, что моноидальная категория C имеет симметрия γ. Моноид M в C является коммутативный когда μ о γ = μ.
Примеры
- Моноидный объект в Набор, то категория наборов (с моноидальной структурой, индуцированной Декартово произведение ), это моноид в обычном понимании.
- Моноидный объект в Вершина, то категория топологических пространств (с моноидальной структурой, индуцированной топология продукта ), это топологический моноид.
- Моноидный объект в категории моноидов (с прямой продукт моноидов) это просто коммутативный моноид. Это легко следует из Аргумент Экмана – Хилтона.
- Моноидный объект в категории полные джойн-полурешетки Как дела (с моноидальной структурой, индуцированной декартовым произведением) является унитальным квант.
- Моноидный объект в (Ab, ⊗Z, Z ), категория абелевых групп, это звенеть.
- Для коммутативное кольцо р, моноидный объект в
- (р-Мод, ⊗р, р), категория модулей над р, является р-алгебра.
- категория градуированные модули это оцененный р-алгебра.
- то категория сетевых комплексов из р-modules - это дифференциальная градуированная алгебра.
- Моноидный объект в K-Vect, то категория K-векторные пространства (опять же с тензорным произведением), является K-алгебра, а комоноидный объект - это K-коалгебра.
- Для любой категории C, категория [C,C] своего эндофункторы имеет моноидальную структуру, индуцированную композицией и тождеством функтор яC. Моноидный объект в [C,C] это монада на C.
- Для любой категории с конечные продукты, каждый объект становится комоноидным объектом через диагональный морфизм . Дважды в категории с конечные копроизведения каждый объект становится моноидным объектом через .
Категории моноидов
Учитывая два моноида (M, μ, η) и (М ', μ ', η ') в моноидальной категории C, морфизм ж : M → M ' это морфизм моноидов когда
- ж о μ = μ ' о (ж ⊗ ж),
- ж о η = η '.
Другими словами, следующие диаграммы
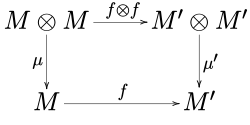 ,
, 
ездить.
Категория моноидов в C а их моноидные морфизмы записываются ПнC.[1]
Смотрите также
- Акт-S, категория моноидов, действующих на множествах
Рекомендации
- ^ Раздел VII.3 в Мак-Лейн, Сондерс (1988). Категории для работающего математика (4-й кор. Печат. Ред.). Нью-Йорк: Springer-Verlag. ISBN 0-387-90035-7.
- Мати Кильп, Ульрих Кнауэр, Александр В. Михалов, Моноиды, Акты и Категории (2000), Вальтер де Грюйтер, Берлин ISBN 3-11-015248-7