Полуэмпирическая формула массы - Semi-empirical mass formula

Ядерная физика
Ядро  · Нуклоны  (п, п ) · Ядерное дело  · Ядерная сила  · Ядерная структура  · Ядерная реакция
Модели ядра Жидкая капля  · Модель ядерной оболочки  · Модель взаимодействующих бозонов  · Ab initio
Нуклиды классификация Изотопы - равный Z Изобары - равный А Изотоны - равный N Исодиаферы - равный N − Z      Изомеры - равно всем вышеперечисленным Зеркальные ядра  – Z ↔ N Стабильный  · Магия  · Даже странно  · Гало  (Борромео )
Ядерная стабильность Связующая энергия  · соотношение p – n  · Капельная линия  · Остров стабильности  · Долина стабильности
Радиоактивный распад Альфа α  · Бета β  (2β, β+ ) · К / л захват  · Изомерный  (Гамма γ  · Внутреннее преобразование ) · Самопроизвольное деление  · Распад кластера  · Эмиссия нейтронов  · Испускание протонов Энергия распада  · Цепочка распада  · Продукт распада  · Радиогенный нуклид
Ядерное деление Спонтанный  · Товары  (разрыв пары ) · Фотоделение
Процессы захвата электрон (2× ) · нейтрон  (s  · р ) · протон  (п  · rp )
Высокоэнергетические процессы Скалывание (космическим лучом ) · Фотодезинтеграция
Нуклеосинтез и ядерная астрофизика Термоядерная реакция Процессы: Звездный  · Большой взрыв  · Сверхновая звезда Нуклиды: Изначальный  · Космогенный  · Искусственный
Ядерная физика высоких энергий Кварк-глюонная плазма  · RHIC  · LHC
Ученые Альварес  · Беккерель  · Быть  · А. Бор  · Н. Бор  · Чедвик  · Кокрофт  · Ir. Кюри  · Пт. Кюри  · Число Пи. Кюри  · Склодовская-Кюри  · Дэвиссон  · Ферми  · Хан  · Дженсен  · Лоуренс  · Mayer  · Meitner  · Олифант  · Оппенгеймер  · Proca  · Перселл  · Раби  · Резерфорд  · Soddy  · Strassmann  · Ąwitecki  · Сцилард  · Кассир  · Томсон  · Уолтон  · Вигнер

В ядерная физика, то полуэмпирическая формула массы (SEMF) (иногда также называемый Формула Вайцзеккера, Формула Бете – Вайцзеккера, или же Формула массы Бете – Вайцзеккера отличить его от Процесс Бете – Вайцзеккера ) используется для аппроксимации масса и различные другие свойства атомное ядро из числа протоны и нейтроны. Как следует из названия, он частично основан на теории, а частично на эмпирических измерениях. Формула представляет модель капли жидкости предложено Георгий Гамов,^[1] который может учитывать большинство членов формулы и дает приблизительные оценки значений коэффициентов. Впервые он был сформулирован в 1935 году немецким физиком. Карл Фридрих фон Вайцзеккер^[2] и хотя на протяжении многих лет в коэффициенты вносились уточнения, структура формулы остается той же сегодня.

Формула дает хорошее приближение для атомных масс и, следовательно, других эффектов. Однако он не может объяснить существование линий с большей энергией связи при определенном количестве протонов и нейтронов. Эти числа, известные как магические числа, являются основой модель ядерной оболочки.

Модель жидкой капли

Иллюстрация членов полуэмпирической формулы массы в капельной модели атомного ядра.

Модель жидкой капли была впервые предложена Георгий Гамов и далее развито Нильс Бор и Джон Арчибальд Уиллер. Он лечит ядро как капля несжимаемой жидкости очень высокой плотности, удерживаемая вместе ядерная сила (остаточный эффект сильная сила ) наблюдается сходство со структурой сферической капли жидкости. В то время как модель жидкой капли является грубой, она учитывает сферическую форму большинства ядер и дает грубый прогноз энергии связи.

Соответствующая массовая формула определяется исключительно количеством протонов и нейтронов, которые она содержит. Исходная формула Вайцзеккера определяет пять терминов:

• Объемная энергия, когда совокупность нуклонов одинакового размера упаковывается в наименьший объем, каждый внутренний нуклон имеет определенное количество других нуклонов, контактирующих с ним. Итак, эта ядерная энергия пропорциональна объему.
• Поверхностная энергия исправляет предыдущее предположение, что каждый нуклон взаимодействует с таким же числом других нуклонов. Этот термин отрицательный и пропорционален площади поверхности, поэтому примерно эквивалентен жидкости. поверхностное натяжение.
• Кулон энергия, потенциальная энергия от каждой пары протонов. Поскольку это сила отталкивания, энергия связи снижается.
• Асимметрия энергии (также называемый Паули Энергия), что составляет Принцип исключения Паули. Неравное количество нейтронов и протонов подразумевает заполнение более высоких уровней энергии для одного типа частиц, в то время как более низкие уровни энергии остаются вакантными для другого типа.
• Парная энергия, что объясняет тенденцию пары протонов и пары нейтронов происходить. Четное число частиц более стабильно, чем нечетное из-за спиновая связь.

Формула

Энергия связи на нуклон (в МэВ ) показано как функция числа нейтронов N и атомного номера Z, заданных полуэмпирической формулой массы. Пунктирная линия показывает нуклиды, обнаруженные экспериментально.

Разница между прогнозируемыми энергиями и известными энергиями связи, выраженная в килоэлектронвольтах. Присутствующие явления можно объяснить другими тонкими терминами, но формула массы не может объяснить наличие линий, которые четко идентифицируются по острым пикам на контурах.

Масса атомного ядра, при ${ displaystyle N}$ нейтроны, ${ displaystyle Z}$ протоны, и поэтому ${ displaystyle A = N + Z}$ нуклоны, дан кем-то

${ displaystyle m = Zm_ {p} + Nm_ {n} - { frac {E_ {B} (N, Z)} {c ^ {2}}}}$

куда ${ displaystyle m_ {p}}$ и ${ displaystyle m_ {n}}$ - масса покоя протона и нейтрона соответственно, а ${ displaystyle E_ {B}}$ это энергия связи ядра. Полуэмпирическая формула массы утверждает, что энергия связи равна:

${ displaystyle E_ {B} = a_ {V} A-a_ {S} A ^ {2/3} -a_ {C} { frac {Z (Z-1)} {A ^ {1/3}} } -a_ {A} { frac {(A-2Z) ^ {2}} {A}} + delta (N, Z)}$^[3]

В ${ displaystyle delta (N, Z)}$ член либо равен нулю, либо ${ displaystyle pm delta _ {0}}$, в зависимости от паритет из ${ displaystyle N}$ и ${ displaystyle Z}$, куда ${ displaystyle delta _ {0} = {a_ {P}} {A ^ {k_ {P}}}}$ для некоторой степени ${ displaystyle k_ {P}}$.

Каждый из членов этой формулы имеет теоретическую основу. Коэффициенты ${ displaystyle a_ {V}}$, ${ displaystyle a_ {S}}$, ${ displaystyle a_ {C}}$, ${ displaystyle a_ {A}}$, и ${ displaystyle a_ {P}}$ определяются эмпирически; хотя они могут быть получены из эксперимента, они обычно выводятся из наименьших квадратов соответствуют современным данным. Хотя обычно он выражается пятью основными терминами, существуют дополнительные термины для объяснения дополнительных явлений. Подобно тому, как изменение полиномиального соответствия изменит его коэффициенты, взаимодействие между этими коэффициентами по мере появления новых явлений является сложным; некоторые термины влияют друг на друга, тогда как ${ displaystyle a_ {P}}$ термин в значительной степени независим.^[4]

Срок действия

Период, термин ${ displaystyle a_ {V} A}$ известен как срок объема. Объем ядра пропорционален А, поэтому этот член пропорционален объему, отсюда и название.

Основанием для этого термина является сильная ядерная сила. Сильное взаимодействие влияет как на протоны, так и на нейтроны, и, как и ожидалось, этот член не зависит от Z. Потому что количество пар, которое можно взять из А частицы ${ Displaystyle { frac {А (А-1)} {2}}}$, можно было бы ожидать члена, пропорционального ${ displaystyle A ^ {2}}$. Однако сильное взаимодействие имеет очень ограниченный диапазон, и данный нуклон может сильно взаимодействовать только со своими ближайшими соседями и следующими ближайшими соседями. Следовательно, количество реально взаимодействующих пар частиц примерно пропорционально А, придавая объемному термину его форму.

Коэффициент ${ displaystyle a_ {V}}$ меньше энергии связи, которой обладают нуклоны по отношению к своим соседям (${ displaystyle E_ {b}}$), что составляет порядка 40 МэВ. Это потому, что чем больше количество нуклоны в ядре, тем больше их кинетическая энергия из-за Принцип исключения Паули. Если рассматривать ядро ​​как Мяч Ферми из ${ displaystyle A}$ нуклоны, с равным числом протонов и нейтронов, то полная кинетическая энергия равна ${ displaystyle {3 over 5} A varepsilon _ {F}}$, с ${ displaystyle varepsilon _ {F}}$ в Энергия Ферми который по оценкам как 28 МэВ. Таким образом, ожидаемое значение ${ displaystyle a_ {V}}$ в этой модели ${ displaystyle E_ {b} - {3 over 5} varepsilon _ {F} sim 17 ; mathrm {МэВ}}$, недалеко от измеренного значения.

Термин поверхности

Период, термин ${ displaystyle a_ {S} A ^ {2/3}}$ известен как поверхностный срок. Этот член, также основанный на сильной силе, является поправкой к члену объема.

Термин объема предполагает, что каждый нуклон взаимодействует с постоянным числом нуклонов, независимо от А. Хотя это почти верно для нуклонов глубоко внутри ядра, эти нуклоны на поверхности ядра имеют меньше ближайших соседей, что оправдывает эту поправку. Это также можно рассматривать как поверхностное натяжение срок, и действительно подобный механизм создает поверхностное натяжение в жидкостях.

Если объем ядра пропорционален А, то радиус должен быть пропорционален ${ displaystyle A ^ {1/3}}$ и площадь поверхности ${ displaystyle A ^ {2/3}}$. Это объясняет, почему поверхностный член пропорционален ${ displaystyle A ^ {2/3}}$. Также можно сделать вывод, что ${ displaystyle a_ {S}}$ должен иметь такой же порядок величины, как ${ displaystyle a_ {V}}$.

Кулоновский член

Период, термин ${ displaystyle a_ {C} { frac {Z (Z-1)} {A ^ {1/3}}}}$ или же ${ displaystyle a_ {C} { frac {Z ^ {2}} {A ^ {1/3}}}}$ известен как Кулон или же электростатический термин.

Основанием для этого термина является электростатическое отталкивание между протонами. В очень грубом приближении ядро ​​можно рассматривать как сферу однородной обвинять плотность. В потенциальная энергия такого распределения заряда можно показать как

${ displaystyle E = { frac {3} {5}} left ({ frac {1} {4 pi varepsilon _ {0}}} right) { frac {Q ^ {2}} { Р}}}$

куда Q это общий заряд и р - радиус сферы. Идентификация Q с ${ displaystyle Ze}$, и отмечая, как выше, что радиус пропорционален ${ displaystyle A ^ {1/3}}$, мы приближаемся к форме кулоновского члена. Однако, поскольку электростатическое отталкивание будет существовать только для более чем одного протона, ${ displaystyle Z ^ {2}}$ становится ${ Displaystyle Z (Z-1)}$. Значение ${ displaystyle a_ {C}}$ можно приблизительно рассчитать, используя приведенное выше уравнение:

Эмпирический ядерный радиус:

${ displaystyle R приблизительно r_ {0} A ^ { frac {1} {3}}.}$

Целые числа квантового заряда:

${ displaystyle Q = Ze }$

${ Displaystyle Z ^ {2} приблизительно Z (Z-1) .}$

Решение заменой:

${ displaystyle E = { frac {3} {5}} left ({ frac {1} {4 pi varepsilon _ {0}}} right) { frac {Q ^ {2}} { R}} = { frac {3} {5}} left ({ frac {1} {4 pi varepsilon _ {0}}} right) { frac {(Ze) ^ {2}} {(r_ {0} A ^ { frac {1} {3}})}} = { frac {3e ^ {2} Z ^ {2}} {20 pi varepsilon _ {0} r_ {0 } A ^ { frac {1} {3}}}} приблизительно { frac {3e ^ {2} Z (Z-1)} {20 pi varepsilon _ {0} r_ {0} A ^ { frac {1} {3}}}} = a_ {C} { frac {Z (Z-1)} {A ^ {1/3}}}}$

Потенциальная энергия распределения заряда:

${ displaystyle E = { frac {3e ^ {2} Z (Z-1)} {20 pi varepsilon _ {0} r_ {0} A ^ { frac {1} {3}}}}}$

Электростатическая кулоновская постоянная:

${ displaystyle a_ {C} = { frac {3e ^ {2}} {20 pi varepsilon _ {0} r_ {0}}}}$

Значение ${ displaystyle a_ {C}}$ с использованием постоянная тонкой структуры:

${ displaystyle a_ {C} = { frac {3} {5}} left ({ frac { hbar c alpha} {r_ {0}}} right) = { frac {3} {5 }} left ({ frac {R_ {P}} {r_ {0}}} right) alpha m_ {p} c ^ {2}}$

куда ${ displaystyle alpha}$ это постоянная тонкой структуры и ${ displaystyle r_ {0} A ^ {1/3}}$ это радиус ядра, давая ${ displaystyle r_ {0}}$ быть приблизительно 1,25 фемтометры. ${ displaystyle R_ {P}}$ - комптоновский радиус протона и ${ displaystyle m_ {p}}$ масса протона. Это дает ${ displaystyle a_ {C}}$ приблизительное теоретическое значение 0,691 МэВ, недалеко от измеренного значения.

${ displaystyle a_ {C} = 0,691 { text {МэВ}}}$

Срок асимметрии

Период, термин ${ displaystyle a_ {A} { frac {(A-2Z) ^ {2}} {A}}}$ известен как член асимметрии (или же Термин Паули). Обратите внимание, что как ${ displaystyle A = N + Z}$, выражение в скобках можно переписать как ${ displaystyle (N-Z)}$. Форма ${ displaystyle (A-2Z)}$ используется для сохранения зависимости от А явный, так как это будет важно для ряда применений формулы.

Теоретическое обоснование этого термина более сложное. В Принцип исключения Паули заявляет, что нет двух идентичный фермионы может занимать точно такое же квантовое состояние в атоме. На данном уровне энергии для частиц доступно лишь конечное число квантовых состояний. В ядре это означает, что по мере "добавления" большего количества частиц эти частицы должны занимать более высокие энергетические уровни, увеличивая общую энергию ядра (и уменьшая энергию связи). Обратите внимание, что этот эффект не основан ни на одной из фундаментальных сил (гравитационный, электромагнитный и др.), только принцип исключения Паули.

Протоны и нейтроны, будучи разными типами частиц, находятся в разных квантовых состояниях. Можно представить себе два разных «пула» состояний, один для протонов, а другой для нейтронов. Теперь, например, если в ядре значительно больше нейтронов, чем протонов, некоторые из нейтронов будут иметь более высокую энергию, чем доступные состояния в протонном пуле. Если бы мы могли переместить некоторые частицы из нейтронного пула в протонный пул, другими словами, преобразовать часть нейтронов в протоны, мы бы значительно уменьшили энергию. Несбалансированность между числом протонов и нейтронов приводит к тому, что энергия оказывается выше, чем она должна быть, для данного количества нуклонов. Это основа для термина асимметрии.

Фактическая форма члена асимметрии может быть снова получена путем моделирования ядра как шара Ферми протонов и нейтронов. Его полная кинетическая энергия составляет

${ displaystyle E_ {k} = {3 over 5} (N_ {p} { varepsilon _ {F}} _ {p} + N_ {n} { varepsilon _ {F}} _ {n})}$

куда ${ displaystyle N_ {p}}$, ${ displaystyle N_ {n}}$ - числа протонов и нейтронов и ${ displaystyle { varepsilon _ {F}} _ {p}}$, ${ displaystyle { varepsilon _ {F}} _ {n}}$ их Энергии Ферми. Поскольку последние пропорциональны ${ displaystyle {N_ {p}} ^ {2/3}}$ и ${ displaystyle {N_ {n}} ^ {2/3}}$соответственно получается

${ displaystyle E_ {k} = C (N_ {p} ^ {5/3} + N_ {n} ^ {5/3})}$ для некоторой постоянной C.

Ведущее расширение в разнице ${ displaystyle N_ {n} -N_ {p}}$ затем

${ displaystyle E_ {k} = {C over 2 ^ {2/3}} left ((N_ {p} + N_ {n}) ^ {5/3} + {5 over 9} {(N_ {n} -N_ {p}) ^ {2} over (N_ {p} + N_ {n}) ^ {1/3}} right) + O ((N_ {n} -N_ {p}) ^ {2}).}$

В разложении нулевого порядка кинетическая энергия равна Энергия Ферми ${ Displaystyle varepsilon _ {F} Equiv { varepsilon _ {F}} _ {p} = { varepsilon _ {F}} _ {n}}$ умножается на ${ Displaystyle {3 более 5} (N_ {p} + N_ {n}) ^ {2/3}}$. Таким образом мы получаем

${ displaystyle E_ {k} = {3 over 5} varepsilon _ {F} (N_ {p} + N_ {n}) + {1 over 3} varepsilon _ {F} {(N_ {n} -N_ {p}) ^ {2} over (N_ {p} + N_ {n})} + O ((N_ {n} -N_ {p}) ^ {4}) = {3 over 5} varepsilon _ {F} A + {1 over 3} varepsilon _ {F} {(A-2Z) ^ {2} over A} + O ((A-2Z) ^ {4}).}$

Первый член вносит вклад в объемный член в полуэмпирической формуле массы, а второй член минус член асимметрии (помните, что кинетическая энергия вносит вклад в общую энергию связи с отрицательный знак).

${ displaystyle varepsilon _ {F}}$ 38 лет МэВ, поэтому расчет ${ displaystyle a_ {A}}$ из приведенного выше уравнения мы получаем только половину измеренного значения. Расхождение объясняется тем, что наша модель не точна: нуклоны фактически взаимодействуют друг с другом, а не равномерно распределены по ядру. Например, в модель оболочки, протон и нейтрон с перекрытием волновые функции будет больше сильное взаимодействие между ними и более сильная энергия связи. Это делает энергетически выгодным (т.е. имеющим более низкую энергию), чтобы протоны и нейтроны имели одинаковые квантовые числа (кроме изоспин ), и, таким образом, увеличивают затраты энергии на асимметрию между ними.

Термин асимметрии можно также понять интуитивно следующим образом. Это должно зависеть от абсолютная разница ${ displaystyle | N – Z |}$, а форма ${ displaystyle (A-2Z) ^ {2}}$ просто и дифференцируемый, что важно для некоторых приложений формулы. Кроме того, небольшие различия между Z и N не имеют высоких затрат энергии. В А в знаменателе отражает тот факт, что данная разница ${ displaystyle | N – Z |}$ менее значимо для больших значений А.

Срок сопряжения

Величина члена спаривания в полной энергии связи для четно-четных и нечетно-нечетных ядер как функция массового числа. Показаны две посадки (синяя и красная линия). Термин спаривания (положительный для четно-четных и отрицательный для нечетно-нечетных ядер) был получен из данных об энергии связи в: G. Audi et al., «Оценка атомной массы AME2012», в Chinese Physics C 36 (2012/12 ) С. 1287–1602.

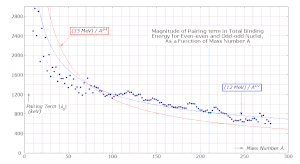
Период, термин ${ displaystyle delta (A, Z)}$ известен как срок сопряжения (возможно также известное как попарное взаимодействие). Этот термин отражает эффект вращение -связь. Выдается:^[5]

${ displaystyle delta (A, Z) = { begin {case} + delta _ {0} & Z, N { text {even}} (A { text {even}}) 0 & A { text {odd}} - delta _ {0} & Z, N { text {odd}} (A { text {even}}) end {case}}}$

куда ${ displaystyle delta _ {0}}$ эмпирически установлено, что его значение составляет около 1000 кэВ, которое медленно уменьшается с массовым числомА. Зависимость от массового числа обычно параметризуется как

${ displaystyle delta _ {0} = {a_ {P}} {A ^ {k_ {P}}}.}$

Значение показателя степени k_п определяется из экспериментальных данных об энергии связи. В прошлом его значение часто принималось равным −3/4, но современные экспериментальные данные показывают, что значение −1/2 ближе к отметке:

${ displaystyle delta _ {0} = {a_ {P}} {A ^ {- 1/2}}}$ или же ${ displaystyle delta _ {0} = {a_ {P} prime} {A ^ {- 3/4}}}$.

Из-за Принцип исключения Паули ядро имело бы меньшую энергию, если бы количество протонов со спином вверх было равно количеству протонов со спином вниз. Это верно и для нейтронов. Только если оба Z и N Даже протоны и нейтроны могут иметь одинаковое количество частиц со спином вверх и вниз. Это эффект, аналогичный члену асимметрии.

Фактор ${ displaystyle A ^ {k_ {P}}}$ трудно объяснить теоретически. Расчет шара Ферми, который мы использовали выше, основанный на модели жидкой капли, но без учета взаимодействий, даст ${ displaystyle A ^ {- 1}}$ зависимость, как в члене асимметрии. Это означает, что реальный эффект для больших ядер будет больше, чем ожидалось по этой модели. Это следует объяснить взаимодействиями между нуклонами; Например, в модель оболочки, два протона с одинаковыми квантовыми числами (кроме вращение ) будет полностью перекрываться волновые функции и таким образом будет иметь больше сильное взаимодействие между ними и более сильная энергия связи. Это делает энергетически выгодным (т.е. имеющим более низкую энергию), чтобы протоны образовывали пары противоположного спина. То же самое и с нейтронами.

Расчет коэффициентов

Коэффициенты рассчитываются путем подгонки к экспериментально измеренным массам ядер. Их значения могут варьироваться в зависимости от того, как они соответствуют данным и какая единица измерения используется для выражения массы. Ниже приведены несколько примеров.

	Айсберг и Резник[6]	По методу наименьших квадратов (1)	По методу наименьших квадратов (2)[7]	Рольф[8]	Wapstra[9]
единица измерения	ты	МэВ	МэВ	МэВ	МэВ
${ displaystyle a_ {V}}$	0.01691	15.8	15.76	15.75	14.1
${ displaystyle a_ {S}}$	0.01911	18.3	17.81	17.8	13
${ displaystyle a_ {C}}$	0.000673[α]	0.714	0.711	0.711	0.595
${ displaystyle a_ {A}}$	0.10175	23.2	23.702	23.7	19
${ displaystyle a_ {P}}$	0.012	12	34	11.18	33.5
${ displaystyle k_ {P}}$	−1/2	−1/2	−3/4	−1/2	−3/4
${ displaystyle delta _ {0}}$ (даже-даже)	${ displaystyle -0,012 над A ^ {1/2}}$	${ displaystyle +12 над A ^ {1/2}}$	${ displaystyle +34 over A ^ {3/4}}$	${ displaystyle +11,18 над A ^ {1/2}}$	${ displaystyle +33,5 over A ^ {3/4}}$
${ displaystyle delta _ {0}}$ (нечетное-нечетное)	${ displaystyle +0,012 над A ^ {1/2}}$	${ displaystyle -12 над A ^ {1/2}}$	${ displaystyle -34 over A ^ {3/4}}$	${ displaystyle -11.18 over A ^ {1/2}}$	${ displaystyle -33,5 over A ^ {3/4}}$
${ displaystyle delta _ {0}}$ (четно-нечетное, нечетное-четное)	0	0	0	0	0
^ Эта модель использует ${ displaystyle Z ^ {2}}$ в числителе кулоновского члена.

Формула не учитывает внутренние структура оболочки ядра.

Таким образом, полуэмпирическая формула массы хорошо подходит для более тяжелых ядер и плохо подходит для очень легких ядер, особенно ⁴Он. Для легких ядер обычно лучше использовать модель, учитывающую эту структуру оболочки.

Примеры следствий формулы

Максимизируя E_б(А,Z) относительно Z, можно было бы найти лучшее нейтронно-протонное отношение N / Z для заданного атомного веса А.^[8] Мы получили

${ displaystyle N / Z приблизительно 1 + { frac {a_ {C}} {2a_ {A}}} A ^ {2/3}.}$

Это примерно 1 для легких ядер, но для тяжелых это отношение растет в хорошем соответствии с эксперимент.

Подставляя указанное выше значение Z обратно в E_б, можно получить энергию связи как функцию атомного веса, E_б(А). E_б(А)/А относительно А дает ядро, которое наиболее сильно связано, т.е. наиболее стабильно.Мы получаем значение А = 63 (медь ), близко к измеренные значения из А = 62 (никель ) и А = 58 (утюг ).

Модель жидкой капли также позволяет вычислить барьеры деления для ядер, которые определяют устойчивость ядра к спонтанное деление. Первоначально предполагалось, что элементы за пределами атомного номера 104 не могут существовать, поскольку они будут подвергаться делению с очень коротким периодом полураспада,^[10] хотя эта формула не учитывала стабилизирующие эффекты замкнутых ядерные снаряды. Модифицированная формула, учитывающая оболочечные эффекты, воспроизводит известные данные и предсказанные остров стабильности (в котором барьеры деления и периоды полураспада, как ожидается, увеличиваются, достигая максимума при закрытии оболочки), хотя также предполагает возможный предел существования сверхтяжелых ядер за пределами Z = 120 и N = 184.^[10]

Рекомендации

Источники

• Freedman, R .; Янг, Х. (2004). Физика Университета Сирса и Земанского с современной физикой (11-е изд.). С. 1633–1634. ISBN  978-0-8053-8768-1.
• Ливерхант, С. Э. (1960). Элементарное введение в физику ядерных реакторов. Джон Уайли и сыновья. стр.58–62. LCCN  60011725.
• Choppin, G .; Liljenzin, J.-O .; Ридберг, Дж. (2002). «Ядерная масса и стабильность» (PDF). Радиохимия и ядерная химия (3-е изд.). Баттерворт-Хайнеманн. С. 41–57. ISBN  978-0-7506-7463-8.

внешняя ссылка

• Модель ядерной жидкой капли в гиперфизика онлайн-ссылка на Государственный университет Джорджии.
• Модель жидкой капли с подгонкой параметров из Первые наблюдения возбужденных состояний в нейтронно-дефицитных ядрах ^160,161W и ¹⁵⁹Та, Алекс Кинан, кандидатская диссертация, Ливерпульский университет, 1999 (HTML версия ).