Звездный параллакс - Stellar parallax

Звездный параллакс является основой для парсек, которое является расстоянием от солнце для астрономический объект что есть параллакс угол одного угловая секунда. (1 Австралия и 1 парсек не в масштабе, 1 парсек = ~ 206265 AU)

Звездный параллакс это видимое смещение положения любой ближайшей звезды (или другого объекта) на фоне далеких объектов. Создано разными орбитальные позиции Земли, чрезвычайно малое наблюдаемое смещение является наибольшим в интервалы времени примерно в шесть месяцев, когда Земля приближается к противоположным сторонам Солнца по своей орбите, что дает базовое расстояние около двух астрономические единицы между наблюдениями. В параллакс сам считается равным половине этого максимума, что примерно эквивалентно наблюдаемому сдвигу, который произошел бы из-за различного положения Земли и Солнца, базовой линии в один астрономическая единица (Австралия).

Звездный параллакс настолько трудно обнаружить, что его существование было предметом многочисленных споров в астрономии на протяжении сотен лет. Фридрих Бессель провел первое успешное измерение параллакса в 1838 г. для звезды 61 Лебедь, используя Fraunhofer гелиометр в Кенигсбергская обсерватория.

Параллакс метод

В течение года отмечается положение звезды S относительно других звезд в ее видимом окружении:

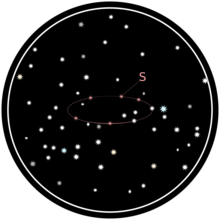
Stellar Parallax Moment.png

Звезды, которые, казалось, не двигались относительно друг друга, используются как ориентиры для определения пути S.

Наблюдаемый путь представляет собой эллипс: проекцию орбиты Земли вокруг Солнца через точку S на удаленный фон неподвижных звезд. Чем дальше S удаляется от оси орбиты Земли, тем больше эксцентриситет траектории S. Центр эллипса соответствует точке, в которой S будет видна с Солнца:

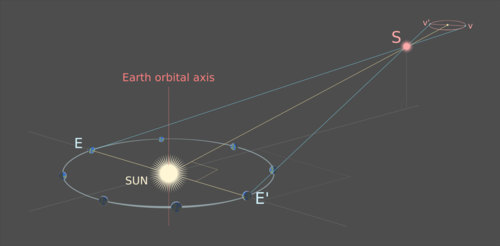
Звездный параллакс, прямой угол наблюдения.png

Плоскость орбиты Земли расположена под углом к ​​линии, идущей от Солнца через S. Вершины v и v 'эллиптической проекции пути S являются проекциями положений Земли E и E', так что линия E-E 'пересекает линию Sun-S под прямым углом; треугольник, образованный точками E, E ’и S, является равнобедренным треугольником с линией Солнце-S в качестве оси симметрии.

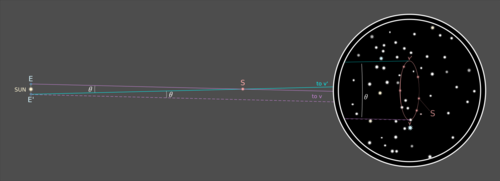
Любые звезды, которые не двигались между наблюдениями, для точности измерения находятся бесконечно далеко. Это означает, что расстояние движения Земли по сравнению с расстоянием до этих бесконечно далеких звезд в пределах точности измерения равно 0. Таким образом, луч зрения от первого положения Земли E до вершины v будет практически таким же. как луч обзора от второй позиции Земли E 'к той же вершине v и, следовательно, будет проходить параллельно ей, что невозможно убедительно изобразить на изображении ограниченного размера:

Поскольку прямая E'-v 'является трансверсалью в той же (приблизительно евклидовой) плоскости, что и параллельные прямые Ev и E'-v, из этого следует, что соответствующие углы пересечения этих параллельных прямых с этой трансверсалью совпадают: угол θ между линии зрения Ev и E'-v 'равны углу θ между E'-v и E'-v', который представляет собой угол θ между наблюдаемыми положениями S по отношению к его явно неподвижному звездному окружению.

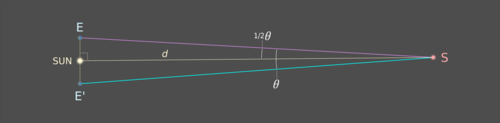
Расстояние d от Солнца к S теперь следует из простой тригонометрии:

загар (½θ) = E-Sun / d,

так что d = E-Sun / tan (½θ), где E-Sun равно 1 AU.

Чем дальше объект находится, тем меньше его параллакс.

Меры звездного параллакса даны в крошечных единицах угловые секунды, или даже в тысячных долях дуги (миллисекунды дуги). Единица измерения расстояния парсек определяется как длина нога из прямоугольный треугольник рядом с угол в одну угловую секунду за один вершина, где длина другой ноги составляет 1 АЕ. Поскольку звездные параллаксы и расстояния включают в себя такие тощие прямоугольные треугольники, можно использовать удобное тригонометрическое приближение для преобразования параллаксов (в угловых секундах) в расстояние (в парсеках). Приблизительное расстояние - это просто взаимный параллакса: Например, Проксима Центавра (ближайшая к Земле звезда, кроме Солнца), параллакс которой составляет 0,7685, находится на расстоянии 1 / 0,7685 парсека = 1,301 парсека (4,24 св. лет).[1]

Ранняя теория и попытки

Гелиометр Доллонда конца 1700-х годов

Звездный параллакс настолько мал, что его нельзя было наблюдать до XIX века, и его очевидное отсутствие использовалось в качестве научного аргумента против гелиоцентризм вовремя ранний современный век. Это ясно из Евклид с геометрия что эффект был бы необнаружимым, если бы звезды находились достаточно далеко, но по разным причинам такие гигантские расстояния казались совершенно неправдоподобными: это был один из Тихо Браге принципиальные возражения против Коперниканский гелиоцентризм что для совместимости с отсутствием наблюдаемого звездного параллакса между орбитой Сатурна и восьмой сферой (неподвижными звездами) должна быть огромная и маловероятная пустота.[2]

Джеймс Брэдли впервые попытался измерить звездные параллаксы в 1729 году. Движение звезды оказалось слишком незначительным для его телескоп, но вместо этого он обнаружил аберрация света[3] и нутация оси Земли и занесены в каталог 3222 звезды.

19 и 20 века

Гелиометр Бесселя
Разделенная линза гелиометра Бамберга (конец 19 века)

Звездный параллакс чаще всего измеряется с помощью годовой параллакс, определяемый как разница в положении звезды при взгляде с Земли и Солнца, то есть угол между звездой и средним радиусом орбиты Земли вокруг Солнца. В парсек (3.26 световых лет ) определяется как расстояние, для которого годовой параллакс равен 1угловая секунда. Годовой параллакс обычно измеряется путем наблюдения за положением звезды в разное время года, когда Земля движется по своей орбите. Измерение годового параллакса было первым надежным способом определения расстояний до ближайших звезд. Первые успешные измерения звездного параллакса были выполнены Фридрих Бессель в 1838 году для звезды 61 Лебедь используя гелиометр.[4][5]

Поскольку к концу XIX века было очень трудно измерить звездные параллаксы, было получено всего около 60 звездных параллаксов, в основном с помощью ниточный микрометр. Астрографы используя астрономические фотопластинки ускорили этот процесс в начале 20 века. Автоматизированные листоизмерительные машины[6] и более сложные компьютерные технологии 1960-х годов позволили более эффективно собирать звездные каталоги. В 1980-х годах устройства с зарядовой связью (ПЗС) заменили фотографические пластины и снизили оптическую погрешность до одной миллисекунды.[нужна цитата ]

Звездный параллакс остается стандартом для калибровки других методов измерения (см. Лестница космических расстояний ). Для точных расчетов расстояния на основе звездного параллакса требуется измерение расстояния от Земли до Солнца, что теперь известно с высокой точностью, основанной на радар отражение от поверхностей планет.[7]

Углы, используемые в этих расчетах, очень малы, и поэтому их трудно измерить. Ближайшая к Солнцу звезда (а также звезда с наибольшим параллаксом), Проксима Центавра, имеет параллакс 0,7685 ± 0,0002 угловой секунды.[1] Этот угол примерно равен поданный объектом диаметром 2 сантиметра, находящимся на расстоянии 5,3 км.

Большой гелиометр был установлен в г. Обсерватория Каффнера (В Вене) в 1896 году и использовался для измерения расстояния до других звезд по тригонометрическому параллаксу.[8] К 1910 году он вычислил 16 параллаксных расстояний до других звезд из всего 108, известных науке в то время.[8]

Схема гелиометра 1911 г. Британская энциклопедия, который был бы видом на разделенную линзу гелиометра

Космическая астрометрия по параллаксу

Точное измерение звездных расстояний Хаббла было расширено в 10 раз на Млечный Путь.[9]

В 1989 году спутник Hipparcos был запущен в первую очередь для получения параллаксов и правильные движения близких звезд, увеличивая количество звездных параллаксов, измеренных с точностью до миллисекунды, в тысячу раз. Тем не менее, Hipparcos может измерять углы параллакса только для звезд размером до 1600 световых лет на расстоянии чуть более одного процента диаметра Млечный путь.

Телескоп Хаббла WFC3 теперь имеет точность от 20 до 40 микросекунд, что позволяет надежно измерять расстояние до 3066 парсек (10 000 световых лет) для небольшого числа звезд.[10] Это дает большую точность Лестница космических расстояний и улучшает знания о расстояниях во Вселенной, основываясь на размерах орбиты Земли.

В Европейское космическое агентство с Миссия Gaia, запущенная 19 декабря 2013 года, как ожидается, будет измерять углы параллакса с точностью до 10 микрон.угловые секунды для всех умеренно ярких звезд, таким образом нанося на карту близлежащие звезды (и потенциально планеты) на расстоянии до десятков тысяч световых лет от Земли.[11] В выпуске данных 2 за 2018 год утверждается, что средние ошибки для параллаксов 15-й звездной величины и более ярких звезд составляют 20-40 микросекунд.[12]

Радиоастрометрия для параллакса

Интерферометрия с очень длинной базой в радиодиапазоне может давать изображения с угловым разрешением около 1 миллисекунды, и, следовательно, для ярких радиоисточников точность измерений параллакса, сделанных в радио, может легко превзойти точность оптических телескопов, таких как Gaia. Эти измерения имеют тенденцию быть ограниченными по чувствительности и должны выполняться по одному, поэтому работа обычно выполняется только для таких источников, как пульсары и рентгеновские двойные системы, где радиоизлучение является сильным по сравнению с оптическим излучением.[нужна цитата ]

Другие исходные данные

Статистический параллакс

Два связанных метода позволяют определять средние расстояния до звезд путем моделирования движения звезд. Оба называются статистическими параллаксами, или отдельные, называемые вековыми параллаксами и классическими статистическими параллаксами.

Движение Солнца в космосе обеспечивает более длинную базовую линию, которая увеличит точность измерений параллакса, известного как вековой параллакс. Для звезд в диске Млечного Пути это соответствует средней базе 4 а.е. в год, тогда как для гало звезды базовый уровень - 40 AU в год. Через несколько десятилетий базовая линия может быть на несколько порядков больше, чем базовая линия Земля – Солнце, используемая для традиционного параллакса. Однако вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость других звезд является дополнительной неизвестной. Применительно к выборкам из нескольких звезд неопределенность может быть уменьшена; точность обратно пропорциональна квадратный корень размера выборки.[13]

Средние параллаксы и расстояния до большой группы звезд можно оценить по их лучевые скорости и правильные движения. Это известно как классический статистический параллакс. Движение звезд моделируется для статистического воспроизведения дисперсии скоростей на основе их расстояния.[13][14]

Другой параллакс в астрономии

Другие варианты использования термина параллакс в астрономии, ни в одном из которых фактически не используется параллакс, являются фотометрический метод параллакса, спектроскопический параллакс, и динамический параллакс.

Смотрите также

Рекомендации

  1. ^ а б Brown, A.G.A .; и другие. (Коллаборация Gaia) (август 2018 г.). "Гайя Выпуск данных 2: сводка содержания и свойств опроса ". Астрономия и астрофизика. 616. A1. arXiv:1804.09365. Bibcode:2018A & A ... 616A ... 1G. Дои:10.1051/0004-6361/201833051.
  2. ^ См. Стр.51 в Прием гелиоцентрической теории Коперника: материалы симпозиума, организованного Комитетом Николая Коперника Международного союза истории и философии науки, Торунь, Польша, 1973, изд. Ежи Добжицки, Международный союз истории и философии науки. Комитет Николая Коперника; ISBN  90-277-0311-6, ISBN  978-90-277-0311-8
  3. ^ Буххайм, Роберт (4 октября 2007 г.). Небо - твоя лаборатория. ISBN  978-0-387-73995-3. Стр.184.
  4. ^ Зейлик и Грегори 1998, п. 44.
  5. ^ Бессель, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans В архиве 2007-06-24 на Wayback Machine " (1838) Astronomische Nachrichten, т. 16. С. 65–96.
  6. ^ ЦЕРН машина для измерения бумаги на пластинах USNO StarScan
  7. ^ Зейлик и Грегори 1998, § 22-3.
  8. ^ а б Хабисон, Питер (1998). «Астрометрия и ранняя астрофизика в обсерватории Каффнера в конце 19 века». Acta Historica Astronomiae. 3: 93–94. Bibcode:1998AcHA .... 3 ... 93H. ISSN  0003-2670.
  9. ^ «Хаббл растягивает звездную рулетку в десять раз дальше». ESA / Hubble Images. Получено 12 апреля 2014.
  10. ^ Harrington, J.D .; Вильярд, Рэй (10 апреля 2014 г.). «Хаббл НАСА продлевает звездную ленту в 10 раз дальше в космос». НАСА. Получено 17 октября 2014.Рисс, Адам Г.; Казертано, Стефано; Андерсон, Джей; Макенти, Джон; Филиппенко, Алексей В. (2014). "Параллакс за пределами килопарсека от пространственного сканирования широкоугольной камерой 3 на космическом телескопе Хаббла". Астрофизический журнал. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ ... 785..161R. Дои:10.1088 / 0004-637X / 785/2/161.
  11. ^ Хенни, Пол Дж. «Миссия ESA Gaia по изучению звезд». Астрономия сегодня. Получено 8 марта 2008.
  12. ^ Brown, A.G.A .; и другие. (Коллаборация Gaia) (август 2018 г.). "Гайя Выпуск данных 2: сводка содержания и свойств опроса ". Астрономия и астрофизика. 616. A1. arXiv:1804.09365. Bibcode:2018A & A ... 616A ... 1G. Дои:10.1051/0004-6361/201833051.
  13. ^ а б Поповский, Петр; Гулд, Эндрю (29 января 1998 г.). «Математика статистического параллакса и локальной шкалы расстояний». arXiv:Astro-ph / 9703140. Bibcode:1997astro.ph..3140P. Цитировать журнал требует | журнал = (помощь)
  14. ^ Layden, Andrew C; Хэнсон, Роберт Б; Хоули, Сюзанна Л; Клемола, Арнольд Р.; Хэнли, Кристофер Дж (1996). "Абсолютная величина и кинематика звезд RR Лиры через статистический параллакс". Астрономический журнал. 112: 2110. arXiv:Astro-ph / 9608108. Bibcode:1996AJ .... 112.2110L. Дои:10.1086/118167.

дальнейшее чтение

  • Дайсон, Ф. В. (1915). «Измерение расстояний до звезд». Обсерватория. 38: 292. Bibcode:1915Обс .... 38..292Д.