Звездная структура - Stellar structure

Сечение Солнца

Звездная структура модели описывают внутреннюю структуру звезда подробно и делать прогнозы о яркость, то цвет и будущая эволюция звезды. Звезды разных классов и возрастов имеют разную внутреннюю структуру, отражающую их элементаль механизмы подпитки и переноса энергии.

Энергетический транспорт

Различные механизмы переноса звезд малой, средней и большой массы

Различные слои звезд по-разному переносят тепло и наружу, в первую очередь конвекция и перенос излучения, но теплопроводность важно в белые карлики.

Конвекция является доминирующим способом переноса энергии, когда градиент температуры достаточно крутой, так что данный газовый пакет внутри звезды будет продолжать расти, если он немного поднимется через адиабатический процесс. В этом случае восходящая посылка жизнерадостный и продолжает расти, если он теплее окружающего газа; если поднимающаяся частица холоднее окружающего газа, она упадет до своей исходной высоты.^[1] В регионах с низким температурным градиентом и достаточно низким непрозрачность чтобы обеспечить перенос энергии посредством излучения, излучение является доминирующим способом передачи энергии.

Внутреннее устройство главная последовательность звезда зависит от массы звезды.

В звездах массой 0,3–1,5 солнечные массы (M_☉ ), включая Солнце, синтез водорода с гелием происходит в основном за счет протон-протонные цепи, которые не создают резкого температурного градиента. Таким образом, во внутренней части звезд солнечной массы преобладает излучение. Внешняя часть звезд солнечной массы достаточно холодна, чтобы водород был нейтральным и, следовательно, непрозрачным для ультрафиолетовых фотонов, поэтому конвекция преобладает. Следовательно, у звезд солнечной массы есть радиационные ядра с конвективными оболочками во внешней части звезды.

У массивных звезд (больше примерно 1,5 M_☉ ), температура ядра выше примерно 1,8 × 10⁷ K, так водород -к-гелий слияние происходит в основном через Цикл CNO. В цикле CNO скорость генерации энергии масштабируется как температура в 15-й степени, тогда как скорость масштабируется как температура в 4-й степени в протон-протонных цепочках.^[2] Из-за сильной температурной чувствительности цикла CNO градиент температуры во внутренней части звезды достаточно крутой, чтобы сделать ядро конвективный. Во внешней части звезды градиент температуры меньше, но температура достаточно высока, чтобы водород почти полностью ионизировался, поэтому звезда остается прозрачной для ультрафиолетового излучения. Таким образом, массивные звезды имеют радиационный конверт.

Звезды главной последовательности с наименьшей массой не имеют зоны излучения; доминирующим механизмом переноса энергии по всей звезде является конвекция.^[3]

Уравнения звездного строения

Профиль температуры на Солнце

Масса внутри заданного радиуса на Солнце

Профиль плотности на Солнце

Профиль давления на Солнце

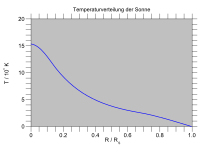
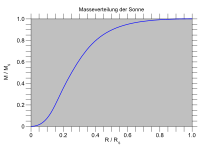
Самый простой обычно используемый модель звездной структуры является сферически-симметричной квазистатической моделью, которая предполагает, что звезда находится в устойчивое состояние и что это сферически симметричный. Он содержит четыре основных дифференциальные уравнения первого порядка: два представляют, как иметь значение и давление варьироваться в зависимости от радиуса; два представляют, как температура и яркость варьируются в зависимости от радиуса.^[4]

При формировании уравнения структуры звезды (используя предполагаемую сферическую симметрию), рассматривается вопрос плотность ${ displaystyle rho (r)}$, температура ${ Displaystyle Т (г)}$, полное давление (вещество плюс излучение) ${ Displaystyle P (r)}$, светимость ${ displaystyle l (r)}$, и скорость генерации энергии на единицу массы ${ displaystyle epsilon (r)}$ в сферической оболочке толщиной ${ displaystyle { mbox {d}} r}$ На расстоянии ${ displaystyle r}$ от центра звезды. Предполагается, что звезда находится в локальное термодинамическое равновесие (LTE), поэтому температура для вещества и фотоны. Хотя LTE строго не соблюдается, потому что температура, которую данная оболочка "видит" под собой, всегда выше, чем температура выше, это приближение обычно превосходно, потому что фотон длина свободного пробега, ${ displaystyle lambda}$, намного меньше длины, на которой температура значительно меняется, т.е. е. ${ displaystyle lambda ll T / | nabla T |}$.

Во-первых, это заявление гидростатическое равновесие: внешняя сила из-за градиент давления внутри звезды точно уравновешивается внутренней силой из-за сила тяжести. Иногда это называют звездным равновесием.

${ displaystyle {{ mbox {d}} P over { mbox {d}} r} = - {Gm rho over r ^ {2}}}$,

где ${ Displaystyle м (г)}$ - кумулятивная масса внутри оболочки при ${ displaystyle r}$ и г это гравитационная постоянная. Суммарная масса увеличивается с радиусом в соответствии с уравнение неразрывности:

${ displaystyle {{ mbox {d}} m over { mbox {d}} r} = 4 pi r ^ {2} rho.}$

Интеграция уравнение неразрывности массы от центра звезды (${ displaystyle r = 0}$) до радиуса звезды (${ displaystyle r = R}$) дает полную массу звезды.

Учет энергии, покидающей сферическую оболочку, дает уравнение энергии:

${ displaystyle {{ mbox {d}} l over { mbox {d}} r} = 4 pi r ^ {2} rho ( epsilon - epsilon _ { nu})}$,

где ${ displaystyle epsilon _ { nu}}$ светимость, создаваемая в виде нейтрино (которые обычно покидают звезду, не взаимодействуя с обычным веществом) на единицу массы. За пределами ядра звезды, где происходят ядерные реакции, энергия не генерируется, поэтому светимость постоянна.

Уравнение переноса энергии принимает разные формы в зависимости от вида транспорта энергии. Для проводящего переноса энергии (подходит для белый Гном ) уравнение энергии имеет вид

${ displaystyle {{ mbox {d}} T over { mbox {d}} r} = - {1 over k} {l over 4 pi r ^ {2}},}$

где k это теплопроводность.

В случае радиационного переноса энергии, подходящего для внутренней части солнечной массы главная последовательность звезда и внешняя оболочка массивной звезды главной последовательности,

${ displaystyle {{ mbox {d}} T over { mbox {d}} r} = - {3 kappa rho l over 64 pi r ^ {2} sigma T ^ {3}} ,}$

где ${ displaystyle kappa}$ это непрозрачность по делу, ${ displaystyle sigma}$ это Постоянная Стефана – Больцмана, а Постоянная Больцмана установлен на единицу.

Случай конвективного переноса энергии не имеет известной строгой математической формулировки и включает турбулентность в газе. Конвективный перенос энергии обычно моделируется с использованием теория длины смешения. Это рассматривает газ в звезде как содержащий дискретные элементы, которые примерно сохраняют температуру, плотность и давление своего окружения, но проходят через звезду до характерной длины, называемой длина смешивания.^[5] Для одноатомный идеальный газ, когда конвекция адиабатический, что означает, что пузырьки конвективного газа не обмениваются теплом с окружающей средой, теория длины смешения дает

${ displaystyle {{ mbox {d}} T over { mbox {d}} r} = left (1- {1 over gamma} right) {T over P} {{ mbox { d}} P over { mbox {d}} r},}$

где ${ displaystyle gamma = c_ {p} / c_ {v}}$ это индекс адиабаты, соотношение удельные плавки в газе. (Для полностью ионизированного идеальный газ, ${ displaystyle gamma = 5/3}$.) Когда конвекция не адиабатическая, истинный градиент температуры не определяется этим уравнением. Например, на Солнце конвекция в основании зоны конвекции, около ядра, является адиабатической, а у поверхности - нет. Теория длины смешения содержит два свободных параметра, которые должны быть установлены, чтобы модель соответствовала наблюдениям, так что это феноменологический теория, а не строгая математическая формулировка.^[6]

Также необходимы уравнения состояния, связывающий давление, непрозрачность и скорость генерации энергии с другими локальными переменными, подходящими для материала, такими как температура, плотность, химический состав и т. д. Соответствующие уравнения состояния для давления могут включать закон идеального газа, давление излучения, давление к вырожденным электронам и т. д. Непрозрачность не может быть точно выражена одной формулой. Он рассчитан для различных составов при определенных плотностях и температурах и представлен в виде таблицы.^[7] Звездная структура коды (имеется в виду компьютерные программы, вычисляющие переменные модели) либо интерполируют в сетке плотности-температуры для получения необходимой непрозрачности, либо используют функция подгонки на основе табличных значений. Аналогичная ситуация возникает при точных расчетах уравнения состояния давления. Наконец, скорость производства ядерной энергии рассчитывается из ядерная физика эксперименты с использованием сети реакции для расчета скоростей реакции для каждой отдельной стадии реакции и равновесных содержаний для каждого изотопа в газе.^[6][8]

В сочетании с набором граничные условия, решение этих уравнений полностью описывает поведение звезды. Типичные граничные условия устанавливают значения наблюдаемых параметров соответствующим образом на поверхности (${ displaystyle r = R}$) и центр (${ displaystyle r = 0}$) звезды: ${ Displaystyle P (R) = 0}$, что означает, что давление на поверхности звезды равно нулю; ${ displaystyle m (0) = 0}$, внутри центра звезды нет массы, как это требуется, если бы плотность массы оставалась конечный; ${ Displaystyle m (R) = M}$, полная масса звезды есть масса звезды; и ${ displaystyle T (R) = T_ {eff}}$, температура на поверхности равна эффективная температура звезды.

Хотя современные модели звездной эволюции описывают основные особенности диаграммы цвет – величина необходимо внести важные улучшения, чтобы устранить неопределенности, связанные с ограниченными знаниями о явлениях переноса. Самой сложной задачей остается численное рассмотрение турбулентности.^{[нужна цитата ]} Некоторые исследовательские группы разрабатывают упрощенное моделирование турбулентности в трехмерных расчетах.

Быстрая эволюция

Вышеупомянутая упрощенная модель не подходит без модификации в ситуациях, когда изменение состава происходит достаточно быстро. Уравнение гидростатического равновесия, возможно, потребуется изменить, добавив член радиального ускорения, если радиус звезды изменяется очень быстро, например, если звезда пульсирует в радиальном направлении.^[9] Кроме того, если ядерное горение нестабильно или ядро ​​звезды быстро коллапсирует, к уравнению энергии необходимо добавить член энтропии.^[10]

Смотрите также

• Высота шкалы
• Стандартная солнечная модель

Рекомендации

Источники

• Kippenhahn, R .; Вейгерт, А. (1990), Звездная структура и эволюция, Springer-Verlag
• Хансен, Карл Дж .; Кавалер, Стивен Д .; Тримбл, Вирджиния (2004), Звездные Интерьеры (2-е изд.), Springer, ISBN  0-387-20089-4
• Kennedy, Dallas C .; Блудман, Сидни А. (1997), "Вариационные принципы для звездной структуры", Астрофизический журнал, 484 (1): 329, arXiv:астро-ph / 9610099, Bibcode:1997ApJ ... 484..329K, Дои:10.1086/304333
• Вайс, Ахим; Хиллебрандт, Вольфганг; Томас, Ганс-Кристоф; Риттер, Х. (2004), Принципы звездной структуры Кокса и Джули, Cambridge Scientific Publishers
• Zeilik, Michael A .; Грегори, Стефан А. (1998), Вводная астрономия и астрофизика (4-е изд.), Издательство Saunders College Publishing, ISBN  0-03-006228-4

внешняя ссылка

• код непрозрачности получено ноябрь 2009 г.
• В Желтый код CESAM, звездная эволюция и структура исходный код Fortran
• EZ для развития звезд ZAMS программное обеспечение FORTRAN 90, полученное на основе кода Stellar Evolution Эгглтона, веб-интерфейс можно найти здесь [1].
• Женевские сетки моделей звездной эволюции (некоторые из них включают перемешивание, вызванное вращением)
• В БАСТИ база данных треков звездной эволюции