Тенсегрити - Tensegrity

Простейшая конструкция тенсегрити (призма Т3). Каждый из трех элементов сжатия (зеленый) симметричен двум другим и симметричен от конца до конца. Каждый конец подключен к трем кабелям (красный), которые обеспечивают натяжение и точно определяют положение этого конца так же, как три кабеля в Skylon определите нижний конец его конической стойки.

Стерео изображение

Правая рамка

Левая рамка

Перекрестный обзор( )

Параллельный вид( )

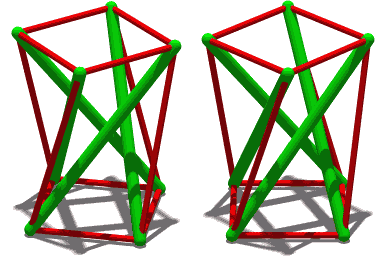
Анимация Аналогичная конструкция, но с четырьмя элементами сжатия.

Тенсегрити, целостность при растяжении или плавающее сжатие это структурный принцип, основанный на системе изолированных компонентов под сжатие внутри сети непрерывных напряжение, и расположены таким образом, что сжатые элементы (обычно стержни или распорки) не касаются друг друга, пока предварительно напряженный натянутые элементы (обычно тросы или связки) очерчивают систему в пространстве.^[1]

Термин был придуман Бакминстер Фуллер в 1960-х как чемодан «натяжной целостности».^[2] Другое название тенсегрити, плавающее сжатие, использовался в основном художником-конструктивистом Кеннет Снельсон.

Концепция

Структуры тенсегрити основаны на сочетании нескольких простых шаблонов проектирования:

• элементы нагружены либо чистым сжатием, либо чистым растяжением, что означает, что конструкция выйдет из строя только в том случае, если кабели деформируются или стержни изгибаются. Это позволяет оптимизировать свойства материала и геометрию поперечного сечения каждого элемента с учетом конкретной нагрузки, которую он несет.
• предварительная нагрузка или напряженный предварительное напряжение позволяет кабелям всегда находиться в напряжении, сохраняя конструктивную целостность.
• механическая стабильность, которая позволяет элементам оставаться в состоянии растяжения / сжатия при увеличении нагрузки на конструкцию. Конструкция также становится более жесткой по мере увеличения натяжения кабеля.

Из-за этих шаблонов ни один структурный элемент не испытывает изгибающий момент и в системе отсутствуют касательные напряжения. Это позволяет создавать исключительно прочные и жесткие конструкции с учетом их массы и поперечного сечения компонентов. Нагрузка хотя бы на некоторые структуры тенсегрити вызывает ауксетический ответ и отрицательный коэффициент Пуассона, например Т3-призма и 6-опорный тенсегрити икосаэдр.

В Skylon на Фестиваль Британии, 1951

Концептуальный строительный блок тенсегрити можно увидеть в 1951 г. Skylon. Шесть кабели, по три на каждом конце, удерживайте башню на месте. Три кабеля, подключенные к дну, «определяют» его местоположение. Остальные три кабеля просто держат его вертикально.

Структура тенсегрити с тремя стержнями (показанная справа) построена на этой более простой структуре: концы каждого зеленого стержня выглядят как верх и низ Skylon. Пока угол между любыми двумя тросами меньше 180 °, положение стержня четко определено. В то время как три кабеля - это минимум, необходимый для устойчивости, дополнительные кабели могут быть прикреплены к каждому узлу в эстетических целях или для обеспечения дополнительной устойчивости. Например, у Снельсона Игольная башня использует повторяющийся шаблон, построенный с использованием узлов, каждый из которых подключен к 5 кабелям.

Элеонора Хартни отмечает, что визуальная прозрачность является важным эстетическим качеством этих структур.^[3] Коркмаз и другие.^[4][5] утверждал, что легкие структуры тенсегрити подходят для адаптивная архитектура.

Приложения

Tensegrities стал широко применяться в архитектуре с 1960-х годов, когда Мацей Гинтовт и Мацей Красиньски разработан Сподек ареновый комплекс (в Катовице, Польша ), как одна из первых основных структур, использующих принцип тенсегрити. Крыша имеет наклонную поверхность, удерживаемую системой тросов, удерживающих ее периметр. Принципы тенсегрити также использовались в Дэвид Гейгер Сеул Олимпийская арена гимнастики (для Летние Олимпийские игры 1988 года ), а Джорджия Доум (для 1996 летние Олимпийские игры ). Поле Тропикана, дом бейсбольной команды высшей лиги Tampa Bay Rays, также имеет купольную крышу, поддерживаемую большой структурой тенсегрити.

Самый большой мост тенсегрити в мире, Курилпинский мост – Брисбен

4 октября 2009 г. Курилпинский мост открыт через Река Брисбен в Квинсленд, Австралия. Вантовый мост с несколькими мачтами, основанный на принципах тенсегрити, в настоящее время является крупнейшим в мире мостом тенсегрити.

12-метровая структура тенсегрити на выставке Наукоград, Калькутта.

С начала 2000-х годов Tensegrities также привлекает внимание робототехников из-за их потенциала в разработке легких и устойчивых роботов. Многочисленные исследователи изучали тенсегрити-вездеходы, био-имитирующие роботы и модульные мягкие роботы. Самый известный робот Тенсегрити - Super Ball^[6], марсоход для исследования космоса, который в настоящее время разрабатывается на НАСА Эймс.

Биология

Биотенсегрити - термин, придуманный доктором Стивеном Левиным, - это применение принципов тенсегрити к биологическим структурам.^[7] Биологические структуры, такие как мышцы, кости, фасция, связки и сухожилия, или жесткий и эластичный клеточные мембраны, сделаны прочными благодаря унисону напряженных и сжатых частей. В скелетно-мышечная система поддерживает напряжение в непрерывной сети мышц и соединительных тканей^[8], в то время как кости обеспечивают прерывистую поддержку сжатия. Даже человеческий позвоночник, который на первый взгляд кажется стопкой позвонки опираясь друг на друга, на самом деле представляет собой структуру тенсегрити.^[9]

Дональд Э. Ингбер разработал теорию тенсегрити для описания многочисленных явлений, наблюдаемых в молекулярная биология.^[10] Например, выраженные формы клеток, будь то их реакции на приложенное давление, взаимодействия с субстратами и т. Д., Все можно математически смоделировать, представляя клетки цитоскелет как тенсегрити. Кроме того, в природе встречаются геометрические узоры (спираль ДНК, геодезический купол вольвокс, Бакминстерфуллерен и др.) также можно понять на основе применения принципов тенсегрити к спонтанной самосборке соединений, белков,^[11] и даже органы. Эта точка зрения подтверждается тем, что взаимодействие натяжения-сжатия тенсегрити минимизирует материал, необходимый для поддержания стабильности и достижения структурной упругости.^[12] Следовательно, естественный отбор давление, вероятно, будет благоприятствовать биологическим системам, организованным тенсегрити.

Как объясняет Ингбер:

Несущие элементы в этих конструкциях - будь то купола Фуллера или скульптуры Снельсона - указывают кратчайшие пути между соседними элементами (и поэтому по определению расположены геодезически). Силы натяжения естественным образом передаются на кратчайшее расстояние между двумя точками, поэтому элементы структуры тенсегрити расположены точно так, чтобы лучше всего выдерживать нагрузку. По этой причине структуры тенсегрити предлагают максимальную силу.^[10]

В эмбриологии Ричард Гордон предложил, чтобы Волны эмбриональной дифференциации размножаются "органеллой дифференциации"^[13] где цитоскелет собрана в бистабильную структуру тенсегрити на апикальном конце клеток, называемую «расщепителем состояний клетки».^[14]

История

Дизайн X-модуля Кеннета Снельсона 1948 года, воплощенный в двухмодульной колонне^[15]

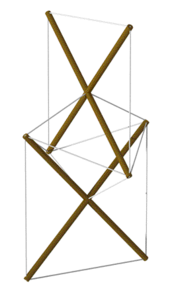
Истоки тенсегрити спорны.^[16] Многие традиционные конструкции, такие как байдарки скин-на-раме и сёдзи аналогичным образом используйте элементы растяжения и сжатия.

В 1948 г. художник Кеннет Снельсон создал свою новаторскую "X-Piece" после художественных изысканий в Black Mountain College (где Бакминстер Фуллер читал лекции) и в других местах. Несколько лет спустя термин «тенсегрити» был придуман Фуллером, наиболее известным благодаря геодезические купола. На протяжении всей своей карьеры Фуллер экспериментировал с включением компонентов растяжения в свою работу, например, при оформлении своего димаксия дома.^[17]

Нововведение Снельсона в 1948 году побудило Фуллера немедленно заказать мачту у Снельсона. В 1949 году Фуллер разработал тенсегрити -икосаэдр на основе этой технологии, и он и его ученики быстро разработали другие конструкции и применили эту технологию для строительства куполов. После перерыва Снельсон также создал множество скульптур, основанных на концепциях тенсегрити. Его основная работа началась в 1959 году, когда была проведена основная выставка в музей современного искусства состоялся. На выставке MOMA Фуллер показал мачту и некоторые другие свои работы.^[18] На этой выставке Снельсон после обсуждения с Фуллером и организаторами выставки кредита на мачту также продемонстрировал некоторые работы в витрина.^[19]

Самая известная работа Снельсона - его 18-метровая высота. Игольная башня 1968 г.

Русский художник Вячеслав Колейчук утверждал, что идея тенсегрити была изобретена Карлис Йохансонс (lv ), советский авангард художник латышский язык спуска, внесший свои работы в главную выставку русских конструктивизм в 1921 г.^[20] Заявление Колейчука было поддержано Мария Гоф за одну из работ на выставке конструктивистов 1921 года.^[21] Снельсон признал, что конструктивисты оказали влияние на его работу (вопрос?).^[22] Французский инженер Давид Жорж Эммерих также отметил, что работы Карлиса Йохансона (и идеи промышленного дизайна), казалось, предвосхищали концепции тенсегрити.^[23]

Стабильность

Призмы Тенсегрити

Трехстержневая структура тенсегрити (3-сторонняя призма) имеет свойство, заключающееся в том, что для заданной (общей) длины «стержня» сжимающего элемента (всего их три) и данной (общей) длины «связки» натяжного троса ( всего шесть), соединяющих концы стержней вместе, существует определенное значение для (общей) длины сухожилия, соединяющего вершины стержней с соседними основаниями стержней, которое заставляет конструкцию сохранять стабильную форму. Для такой конструкции несложно доказать, что треугольник, образованный вершинами стержней, и треугольник, образованный основаниями стержней, повернуты друг относительно друга на угол 5π / 6 (радиан).^[24]

Устойчивость («предварительное напряжение») нескольких двухэтапных структур тенсегрити анализируется Sultan, et al.^[25]

Икосаэдры Тенсегрити

Математическая модель икосаэдра тенсегрити

Разные формы икосаэдров тенсегрити в зависимости от соотношения длин сухожилий и распорок.

Многогранник, непосредственно соответствующий геометрии икосаэдра тенсегрити, называется многогранником. Икосаэдр Джессена. Его сферическая динамика вызвала особый интерес Бакминстера Фуллера.^[26], который сослался на преобразования расширения-сжатия вокруг стабильного равновесия как дрожащее движение.^[27]

Ниже приводится математическая модель фигур, связанных с тенсегрити. икосаэдр, объясняя, почему это устойчивая конструкция, хотя и с бесконечно малой подвижностью.^[28]

Рассмотрим куб с длиной стороны 2dс центром в начале координат. Поместите распорку длины 2л в плоскости каждой грани куба так, чтобы каждая стойка была параллельна одному краю грани и центрировалась на грани. Более того, каждая стойка должна быть параллельна стойке на противоположной грани куба, но ортогональна всем остальным стойкам. Если декартовы координаты одной стойки равны ${ displaystyle (0, d, l)}$ и ${ displaystyle (0, d, -l)}$, его параллельная стойка будет соответственно ${ displaystyle (0, -d, -l)}$ и ${ displaystyle (0, -d, l)}$. Координаты других концов (вершин) стойки получаются путем перестановки координат, например, ${ Displaystyle (0, d, l) rightarrow (d, l, 0) rightarrow (l, 0, d)}$ (вращательная симметрия в главной диагонали куба).

Расстояние s между любыми двумя соседними вершинами (0, d, л) и (d, л, 0) является

$${ Displaystyle s ^ {2} = (dl) ^ {2} + d ^ {2} + l ^ {2} = 2 left (d - { frac {1} {2}} , l right ) ^ {2} + { frac {3} {2}} , l ^ {2}}$$

Представьте себе эту фигуру, построенную из распорок заданной длины. 2л и сухожилия (соединяющие соседние вершины) заданной длины s, с участием ${ displaystyle s> { sqrt { frac {3} {2}}} , l}$. Отношение говорит нам, что есть два возможных значения для d: один реализуется путем сдвига распорок вместе, другой - путем их разъединения. Например, для ${ displaystyle s = { sqrt {2}} , l}$ минимальная фигура (d = 0) это регулярный октаэдр и максимальная цифра (d = л) это квазирегулярный кубооктаэдр. В этом случае ${ displaystyle d = { frac {1} {2}} ({ sqrt {5}} - 1) l}$ у нас есть s = 2d, так что выпуклая оболочка из Золотое сечение фигура (${ displaystyle d = phi}$) это регулярный икосаэдр. Поскольку ни одна статья о кинематике многогранников не будет полной без Coxeter ссылки, здесь уместно отметить, что к 1940 г. (до Икосаэдр Джессена или открытие икосаэдра тенсегрити) Коксетер уже показал, как двенадцать вершин икосаэдра можно получить, разделив двенадцать ребер октаэдра согласно золотому сечению, как одна из непрерывных серий (обычно неправильных) икосаэдров с гранями, состоящими из восьми равносторонних треугольников и двенадцати равнобедренных треугольников, в диапазоне от кубооктаэдра до октаэдра (как предельные случаи), которые могут быть образованы таким процессом деления.^[29]

В частном случае ${ displaystyle s = { sqrt { frac {3} {2}}} , l}$ две крайности совпадают, и ${ displaystyle d = { frac {1} {2}} , l}$, поэтому фигура представляет собой устойчивый икосаэдр тенсегрити.

Поскольку икосаэдр тенсегрити представляет собой экстремальную точку вышеупомянутого соотношения, он имеет бесконечно малую подвижность: небольшое изменение длины s сухожилия (например, растягивая сухожилия) приводит к гораздо большему изменению расстояния 2d стоек.

Патенты

• Патент США 3063521 , «Конструкции с целостностью при растяжении», 13 ноября 1962 г., Бакминстер Фуллер.
• Патент Франции № 1,377,290, «Construction de Reseaux Autotendants», 28 сентября 1964 г., Давид Жорж Эммерих.
• Патент Франции № 1 377 291, «Structures Linéaires Autotendants», 28 сентября 1964 г., Давид Жорж Эммерих.
• Патент США 3139957 , «Подвесное здание» (также называемое осиной), 7 июля 1964 года, Бакминстер Фуллер.
• Патент США 3,169,611 , «Непрерывное растяжение, структура прерывистого сжатия», 16 февраля 1965 г., Кеннет Снельсон.
• Патент США 3866366 , «Несимметричные конструкции с натяжной целостностью», 18 февраля 1975 г., Бакминстер Фуллер.

Базовые структуры тенсегрити

• 

  Самая простая структура тенсегрити, 3-призма

• 

  Еще одна 3-призма

• 

  Аналогичная конструкция, но с четырьмя элементами сжатия.

• 

  Призма прото-тенсегрити Карла Иогансона, 1921 г.^{[галерея 1]}

• 

  Икосаэдр Тенсегрити, Бакминстер Фуллер, 1949^{[галерея 2]}

• 

  Тенсегрити-тетраэдр, Франческо делла Салла, 1952 г.^{[галерея 3]}

• 

  Tensegrity X-Module Tetrahedron, Кеннет Снельсон, 1959^{[галерея 4]}

• 

  Кеннет Снельсон Художественная скульптура "Игольная башня".

• 

  Рассеивать, художественная скульптура башни в виде песочных часов, включая структуру тенсегрити, построенная АфрикаБерн, 2015, а Горящий человек региональное мероприятие

• 

  Робот NASA SUPERball Tensegrity - это ранний прототип, способный приземлиться на другой планете без подушки безопасности, а затем стать мобильным для исследования. Конструкция тенсегрити обеспечивает структурную податливость, поглощая силы удара при приземлении и движение за счет изменения длины кабеля, 2014 г.

• 

  Купол тенсегрити из садовых кольев и нейлонового шпагата, построенный во дворе дома, 2009 г.

Смотрите также

• Мост - конструкция построена так, чтобы преодолевать физические препятствия
• Девятое облако, гигантские парящие в небе сферы тенсегрити, названные Бакминстером Фуллером
• Гиперболоидная структура
• Теория взаимодействий акторов
• Седельная крыша
• Космическая рамка - Жесткая трехмерная несущая ферменная конструкция
• Синергетика
• Тенсарность
• Растяжимая структура
• Тонкостенная структура

Заметки

использованная литература

Список используемой литературы

• Фуллер, Р. Бакминстер (1982) [1975]. Синергетика: исследования геометрии мышления. я. Макмиллан. ISBN  978-0-02-065320-2.
• — (1983) [1979]. Синергетика 2: Дальнейшие исследования геометрии мышления. 2. Макмиллан. ISBN  978-0-02-092640-5. онлайн
• Фуллер, Бакминстер (1961). «Тенсегрити». Ежегодное портфолио и новости искусства (4): 112–127, 144, 148.
• Фуллер, Р. Бакминстер; Маркс, Роберт В. (1973) [1960]. Мир Dymaxion Бакминстера Фуллера. Якорные книги. Рис. 261–280. ISBN  978-0385018043. Хороший обзор объема тенсегрити с точки зрения Фуллера и интересный обзор ранних структур с тщательной атрибуцией большую часть времени.
• Гомес-Хауреги, Валентин (2007). Тенсегридад. Estructuras Tensegríticas en Ciencia y Arte (на испанском). Сантандер: Университет Кантабрии. ISBN  978-84-8102-437-1.
• Гомес-Хауреги, Валентин (2010). Структуры тенсегрити и их применение в архитектуре. Сантандер: Служба публикаций Университета Кантабрии. ISBN  978-84-8102-575-0.
• Коркмаз, Синан; Бел Хадж Али, Низар; Смит, Ян Ф.С. (2011). «Конфигурация системы контроля устойчивости к повреждениям моста Тенсегрити». Передовая инженерная информатика. 26: 145. Дои:10.1016 / j.aei.2011.10.002.
• Коркмаз, Синан; Бел Хадж Али, Низар; Смит, Ян Ф.С. (Июнь 2011 г.). «Определение стратегий контроля устойчивости активной структуры тенсегрити к повреждениям» (PDF). Инженерные сооружения. 33 (6): 1930–9. CiteSeerX  10.1.1.370.6243. Дои:10.1016 / j.engstruct.2011.02.031. Архивировано из оригинал (PDF) 29 сентября 2011 г.
• Лалвани, Хареш, изд. (1996). "Истоки тенсегрити: взгляды Эммериха, Фуллера и Снельсона". Международный журнал космических структур. 11 (1–2): 27–55. Дои:10.1177/026635119601-204. S2CID  114004009.
• Juan, S.J .; Тур, Дж. М. (июль 2008 г.). «Фреймворки тенсегрити: обзор статического анализа». Механизм и теория машин. 43 (7): 859–881. CiteSeerX  10.1.1.574.7510. Дои:10.1016 / j.mechmachtheory.2007.06.010.

дальнейшее чтение

Эта статья включает в себя список общих использованная литература, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшить эта статья введение более точные цитаты. (Март 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

• Ди Карло, Бьяджо. "СТРУКТУРА ТЕНСЕГРАЛИ". Quaderni di Geometria Sinergetica, Пескара 2004. http://www.biagiodicarlo.com
• Эдмондсон, Эми. Более полное объяснение, EmergentWorld LLC, 2007. Более ранняя версия доступна на сайте https://web.archive.org/web/20031002084349/http://www.angelfire.com/mt/marksomers/40.html
• Форбс, Питер (2010) [2006]. «9. Система построения« толкай и тяни »». Нога геккона: как ученые берут отрывок из книги природы. Харпер Коллинз. С. 197–230. ISBN  978-0-00-740547-3.
• Ханаор, Ариэль (1997). «13. Тенсегрити: теория и применение». В Габриэле, Ж. Франсуа (ред.). За гранью куба: архитектура космических рамок и многогранников. Вайли. С. 385–408. ISBN  978-0-471-12261-6.
• Кеннер, Хью (1976). Геодезическая математика и как ее использовать. Калифорнийский университет Press. ISBN  978-0520029248. Репринт 2003 г. ISBN  0520239318. Это хорошая отправная точка для изучения математики тенсегрити и построения моделей.
• Масич, Миленко; Скелтон, Роберт Э .; Гилл, Филип Э. (август 2005 г.). «Формообразование алгебраического тенсегрити». Международный журнал твердых тел и структур. 42 (16–17): 4833–58. Дои:10.1016 / j.ijsolstr.2005.01.014. Они представляют замечательный результат, который линейное преобразование тенсегрити также является тенсегрити.
• Морган, Г.Дж. (2003). «Историческое обозрение: вирусы, кристаллы и геодезические купола». Тенденции в биохимических науках. 28 (2): 86–90. Дои:10.1016 / S0968-0004 (02) 00007-5. PMID  12575996.
• Мотро, Р. (1992). «Системы тенсегрити: современное состояние». Международный журнал космических структур. 7 (2): 75–84. Дои:10.1177/026635119200700201. S2CID  107820090.
• Пью, Энтони (1976). Введение в тенсегрити. Калифорнийский университет Press. ISBN  978-0-520-03055-8. Архивировано из оригинал 4 мая 2008 г.. Получено 9 мая 2008.
• Снельсон, Кеннет (ноябрь 1990 г.). "Письмо к Р. Мотро". Международный журнал космических структур.
• Souza, Thales R .; Fonseca, Sérgio T .; Gonçalves, Gabriela G .; Окарино, Юлиана М .; Манчини, Мариса К. (октябрь 2009 г.). «Престресс выявлен пассивным одновременным натяжением в голеностопном суставе». Журнал биомеханики. 42 (14): 2374–80. Дои:10.1016 / j.jbiomech.2009.06.033. PMID  19647832.
• Вильней, Орен, Кабельные сети и тенсегрические оболочки: приложения для анализа и проектирования, Нью-Йорк: Ellis Horwood Ltd., 1990.
• Ван, Бинь-Бин (1998). «Стойко-тросовые системы: Часть I - Тенсегрити». Журнал исследований конструкционной стали. 45 (3): 281–9. Дои:10.1016 / S0143-974X (97) 00075-8.
• Уилкен, Тимоти. В поисках дара Тенсегрити, TrustMark, 2001.

внешние ссылки

• Научные публикации в области тенсегрити Швейцарский федеральный технологический институт (EPFL), Лаборатория прикладных вычислений и механики (IMAC)
• Сайт Стивена Левина Биотенсегрити Несколько статей хирурга-ортопеда по механике тенсегрити биологических структур от вирусов до позвоночных.