Расчет шкалы времени - Time-scale calculus
В математика, исчисление шкалы времени это объединение теории разностные уравнения с этим из дифференциальные уравнения, объединяющий интеграл и дифференциал исчисление с исчисление конечных разностей, предлагая формализм для изучения гибридных дискретно-непрерывных динамические системы. У него есть приложения в любой области, где требуется одновременное моделирование дискретных и непрерывных данных. Он дает новое определение производной, так что если дифференцировать функцию, определенную на действительных числах, то определение эквивалентно стандартному дифференцированию, но если использовать функцию, определенную на целых числах, то это эквивалентно форвардная разница оператор.
История
Исчисление шкалы времени было введено в 1988 году немецким математиком. Стефан Хильгер.[1] Однако подобные идеи использовались раньше и восходят, по крайней мере, к введению Интеграл Римана – Стилтьеса., объединяющий суммы и интегралы.
Динамические уравнения
Многие результаты, касающиеся дифференциальных уравнений, довольно легко переносятся на соответствующие результаты для разностных уравнений, в то время как другие результаты кажутся полностью отличными от своих. непрерывный аналоги.[2] Изучение динамических уравнений на шкалах времени выявляет такие расхождения и помогает избежать доказательства результатов дважды - один раз для дифференциальных уравнений и еще раз для разностных уравнений. Общая идея состоит в том, чтобы доказать результат для динамического уравнения, в котором область неизвестных функция - это так называемая шкала времени (также известная как набор времени), которая может быть произвольным замкнутым подмножеством вещественных чисел. Таким образом, результаты относятся не только к набор из действительные числа или набор целые числа но к более общим временным шкалам, таким как Кантор набор.
Три самых популярных примера исчисление по шкале времени дифференциальное исчисление, разностное исчисление, и квантовое исчисление. Динамические уравнения в масштабе времени имеют потенциал для приложений, таких как динамика населения. Например, они могут моделировать популяции насекомых, которые непрерывно развиваются в течение сезона, вымирают зимой, пока их яйца инкубируются или находятся в состоянии покоя, а затем вылупляются в новом сезоне, создавая неперекрывающуюся популяцию.
Формальные определения
А шкала времени (или же цепь измерения) это закрытое подмножество из реальная линия . Обычное обозначение для общей шкалы времени: .
Двумя наиболее часто встречающимися примерами шкал времени являются действительные числа и дискретное время шкала .
Отдельная точка на шкале времени определяется как:
Операции на шкалах времени
В прыжок вперед и прыжок назад операторы представляют собой ближайшую точку на шкале времени справа и слева от данной точки , соответственно. Формально:
- (оператор прямого сдвига / перехода)
- (оператор обратного сдвига / перехода)
В зернистость - это расстояние от точки до ближайшей точки справа и определяется как:
Для правильной плотной , и .
Для левого плотного ,
Классификация очков
Для любого , является:
- левый плотный если
- право плотный если
- оставил разбросанным если
- разбросан вправо если
- плотный если обе плотные слева и справа плотные
- изолированные если и слева, и справа, и справа
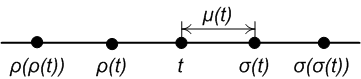
Как показано на рисунке справа:
- Точка является плотный
- Точка является левый плотный и разбросан вправо
- Точка является изолированные
- Точка является оставил разбросанным и право плотный
Непрерывность
Непрерывность шкалы времени переопределяется как эквивалент плотности. Шкала времени называется непрерывный вправо в точке если он плотный в точке . Точно так же масштаб времени называется непрерывный слева в точке если он остается плотным в точке .
Производная
Возьмите функцию:
- ,
(где ℝ может быть любым Банахово пространство, но для простоты установлена реальная линия).
Определение: дельта-производная (также производная Хильгера) существует тогда и только тогда, когда:
Для каждого существует район из такой, что:
для всех в .
Брать потом , , ; производная, используемая в стандарте исчисление. Если (в целые числа ), , , это оператор прямой разницы используется в разностных уравнениях.
Интеграция
В дельта-интеграл определяется как первообразная по отношению к дельта-производной. Если имеет непрерывную производную один набор
Преобразование Лапласа и z-преобразование
А Преобразование Лапласа может быть определен для функций на шкалах времени, которые используют одну и ту же таблицу преобразований для любой произвольной шкалы времени. Это преобразование можно использовать для решения динамических уравнений в масштабах времени. Если шкала времени - неотрицательные целые числа, тогда преобразование равно[2] к измененному Z-преобразование:
Частичная дифференциация
Уравнения с частными производными и уравнения в частных разностях унифицированы как частные динамические уравнения на временных масштабах.[3][4][5]
Множественная интеграция
Множественная интеграция о временных масштабах рассматривается в Bohner (2005).[6]
Стохастические динамические уравнения на временных масштабах
Стохастические дифференциальные уравнения а стохастические разностные уравнения могут быть обобщены на стохастические динамические уравнения во временных масштабах.[7]
Теория меры на шкалах времени
С каждой шкалой времени связана естественная мера[8][9] определяется через
куда обозначает Мера Лебега и - оператор обратного сдвига, определенный на . Дельта-интеграл оказывается обычным Интеграл Лебега – Стилтьеса. по этой мере
и дельта-производная оказывается Производная Радона – Никодима по этой мере[10]
Распределения по шкалам времени
В Дельта Дирака и Дельта Кронекера унифицированы по шкале времени как Дельта Хильгера:[11][12]
Интегральные уравнения на временных масштабах
Интегральные уравнения и уравнения суммирования унифицированы в виде интегральных уравнений на временных масштабах.[нужна цитата ]
Дробное исчисление на шкалах времени
Дробное исчисление по шкале времени рассматривается в Бастосе, Мозырской и Торресе.[13]
Смотрите также
- Анализ на фракталы для динамических уравнений на Кантор набор.
Рекомендации
- ^ Хильгер, Стефан (1989). Ein Maßkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten (Кандидатская диссертация). Universität Würzburg. OCLC 246538565.
- ^ а б Мартин Бонер и Аллан Петерсон (2001). Динамические уравнения на временных шкалах. Birkhäuser. ISBN 978-0-8176-4225-9.
- ^ Ahlbrandt, Calvin D .; Мориан, Кристина (2002). «Уравнения с частными производными на временных масштабах». Журнал вычислительной и прикладной математики. 141 (1–2): 35–55. Bibcode:2002JCoAM.141 ... 35A. Дои:10.1016 / S0377-0427 (01) 00434-4.
- ^ Джексон, Б. (2006). «Частные динамические уравнения на временных масштабах». Журнал вычислительной и прикладной математики. 186 (2): 391–415. Bibcode:2006JCoAM.186..391J. Дои:10.1016 / j.cam.2005.02.011.
- ^ Bohner, M .; Гусейнов, Г. С. (2004). «Частичная дифференциация по шкалам времени» (PDF). Динамические системы и приложения. 13: 351–379.
- ^ Bohner, M; Гусейнов, Г.С. (2005). «Множественная интеграция по временным шкалам». Динамические системы и приложения. CiteSeerX 10.1.1.79.8824.
- ^ Саньял, Суман (2008). Стохастические динамические уравнения (Кандидатская диссертация). Миссурийский университет науки и технологий. ProQuest 304364901.
- ^ Гусейнов, Г. С. (2003). «Интеграция по шкалам времени». J. Math. Анальный. Приложение. 285: 107–127. Дои:10.1016 / S0022-247X (03) 00361-5.
- ^ Дениз, А. (2007). Теория меры на шкалах времени (PDF) (Дипломная работа). Измирский технологический институт.
- ^ Eckhardt, J .; Тешль, Г. (2012). «О связи производных Хильгера и Радона – Никодима». J. Math. Анальный. Приложение. 385 (2): 1184–1189. arXiv:1102.2511. Дои:10.1016 / j.jmaa.2011.07.041.
- ^ Дэвис, Джон М .; Gravagne, Ian A .; Джексон, Билли Дж .; Маркс, Роберт Дж. II; Рамос, Алиса А. (2007). «Снова о преобразовании Лапласа во временных масштабах». J. Math. Анальный. Приложение. 332 (2): 1291–1307. Bibcode:2007JMAA..332.1291D. Дои:10.1016 / j.jmaa.2006.10.089.
- ^ Дэвис, Джон М .; Gravagne, Ian A .; Маркс, Роберт Дж. II (2010). «Двусторонние преобразования Лапласа на шкалах времени: сходимость, свертка и характеристика стационарных стохастических временных рядов». Схемы, системы и обработка сигналов. 29 (6): 1141–1165. Дои:10.1007 / s00034-010-9196-2.
- ^ Bastos, Nuno R.O .; Мозырская, Дорота; Торрес, Дельфим Ф. М. (2011). «Дробные производные и интегралы на шкале времени с помощью обратного обобщенного преобразования Лапласа». Международный журнал математики и вычислений. 11 (J11): 1–9. arXiv:1012.1555. Bibcode:2010arXiv1012.1555B.
дальнейшее чтение
- Агарвал, Рави; Бонер, Мартин; О’Реган, Донал; Петерсон, Аллан (2002). «Динамические уравнения на временных шкалах: обзор». Журнал вычислительной и прикладной математики. 141 (1–2): 1–26. Bibcode:2002JCoAM.141 .... 1A. Дои:10.1016 / S0377-0427 (01) 00432-0.
- Динамические уравнения на временных шкалах Специальный выпуск Журнал вычислительной и прикладной математики (2002)
- Динамические уравнения и приложения Специальный выпуск Успехи в разностных уравнениях (2006)
- Динамические уравнения на шкалах времени: качественный анализ и приложения Специальный выпуск Нелинейная динамика и теория систем (2009)




































![{ mathcal {Z}} ' {x [z] } = { frac {{ mathcal {Z}} {x [z + 1] }} {z + 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0eff16581e442c4142fd193357778ff342911e5)





