Закон Видемана – Франца - Википедия - Wiedemann–Franz law

В физика, то Закон Видемана – Франца утверждает, что отношение электронного вклада теплопроводность (κ) к электрическая проводимость (σ) из металл пропорционально температура (Т).^[1]

${ displaystyle { frac { kappa} { sigma}} = LT}$

Теоретически константа пропорциональности L, известный как Число Лоренца, равно

${ displaystyle L = { frac { kappa} { sigma T}} = { frac { pi ^ {2}} {3}} left ({ frac {k _ { rm {B}}} {e}} right) ^ {2} = 2,44 times 10 ^ {- 8} , mathrm {W , Omega , K ^ {- 2}}.}.$

Этот эмпирический закон назван в честь Густав Видеманн и Рудольф Франц, который в 1853 г. сообщил, что κ/σ имеет примерно одинаковое значение для разных металлов при одинаковой температуре.^[2] Соразмерность κ/σ с температурой был открыт Людвиг Лоренц в 1872 г.

Вывод

Качественно это соотношение основано на том факте, что перенос тепла и электричества включает свободные электроны в металле.

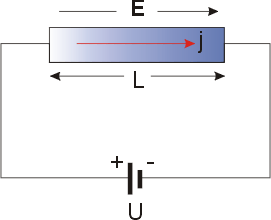
Математическое выражение закона можно получить следующим образом. Электропроводность металлов - хорошо известное явление, связанное с наличием свободных электронов проводимости, которые можно измерить, как показано на рисунке. В плотность тока j наблюдается пропорционально применяемому электрическое поле и следует Закон Ома где префактор - это конкретный электрическая проводимость. Поскольку электрическое поле и плотность тока равны векторов Закон Ома здесь выделен жирным шрифтом. В общем, проводимость можно выразить как тензор второго ранга (3 × 3 матрица ). Здесь мы ограничиваем обсуждение изотропный, т.е. скаляр проводимость. Конкретные удельное сопротивление - величина, обратная проводимости. Оба параметра будут использоваться в дальнейшем.

Друде (ок. 1900 г.) осознал, что феноменологическое описание проводимости можно сформулировать в весьма общем виде (электронная, ионная, теплопроводность и т. д.). Хотя феноменологическое описание для электронов проводимости неверно, оно может служить предварительной обработкой.

Предполагается, что электроны свободно движутся в твердом теле, как в идеальный газ. Сила, приложенная к электрону электрическим полем, приводит к ускорение в соответствии с

${ displaystyle mathbf {F} = -e mathbf {E} = m { frac {; d mathbf {v}} {dt}}}$

${ displaystyle ; d mathbf {v} = - { frac {e mathbf {E}} {m}} dt}$

Однако это привело бы к постоянному ускорению и, в конечном итоге, к бесконечной скорости. Таким образом, дальнейшее предположение состоит в том, что электроны сталкиваются с препятствиями (например, дефекты или же фононы ) время от времени, что ограничивает их свободный полет. Это устанавливает среднее или скорость дрейфа V_d. Скорость дрейфа связана с среднее время рассеяния что видно из следующих соотношений.

${ displaystyle { frac {d mathbf {v}} {dt}} = - { frac {e mathbf {E}} {m}} = { frac {1} { tau}} mathbf { v}}$

Из кинетическая теория газов, ${ displaystyle kappa = { frac {1} {3}} c_ {V} mn , ell , langle v rangle}$, куда ${ displaystyle c_ {V} = 3 { frac {k _ { rm {B}}} {m}}}$ это удельная теплоемкость согласно Закон Дюлонга – Пети, ${ displaystyle ell}$ это длина свободного пробега и ${ displaystyle langle v rangle = { sqrt { frac {8k _ { rm {B}} T} { pi m}}} ​​= { sqrt { frac {8} {3 pi}}} v _ { rm {rms}}}$ это Средняя скорость электронов; Из Модель Друде, ${ displaystyle sigma = { frac {ne ^ {2} tau} {m}} = { frac {ne ^ {2} ell} {m langle v rangle}}}$.

Следовательно, ${ displaystyle { frac { kappa} { sigma}} = { frac {c_ {V} m ^ {2} , langle {v} rangle ^ {2}} {3e ^ {2}} } = { frac {8} { pi}} { frac {k _ { rm {B}} ^ {2} T} {e ^ {2}}}}$, который является законом Видемана – Франца с ошибочным константа пропорциональности ${ displaystyle { frac {8} { pi}} приблизительно 2,55}$; После учета квантовых эффектов (как в Модель Зоммерфельда ), тогда коэффициент пропорциональности корректируется до ${ displaystyle { frac { pi ^ {2}} {3}} приблизительно 3,29}$, что согласуется с экспериментальными значениями.

Температурная зависимость

Значение L₀ = 2.44×10⁻⁸ Вт Ом К⁻² возникает из-за того, что при низких температурах (${ displaystyle T rightarrow 0}$ К) тепловые и зарядовые токи переносятся одними и теми же квазичастицами: электронами или дырками. При конечных температурах два механизма приводят к отклонению отношения ${ Displaystyle L = каппа / ( sigma T)}$ от теоретического значения Лоренца L₀: (i) другие носители тепла, такие как фонон или магноны, (ii) Неупругое рассеяние При приближении температуры к 0 К неупругое рассеяние становится слабым и способствует большему q значения рассеяния (траектория а на рисунке). Для каждого переносимого электрона также переносится тепловое возбуждение, и достигается число Лоренца. L = L₀. Отметим, что в идеальном металле неупругое рассеяние полностью отсутствовало бы в пределе ${ displaystyle T rightarrow 0}$ K и теплопроводность исчезнет ${ displaystyle kappa rightarrow 0; L rightarrow 0}$.При конечной температуре малая q возможны значения рассеяния (траектория b на рисунке) и электрон может перемещаться без переноса теплового возбуждения L(Т) < L₀При более высоких температурах становится важным вклад фононов в теплоперенос в системе. Это может привести к L(Т) > L₀. Выше Температура Дебая фононный вклад в теплоперенос постоянен и отношение L(Т) снова оказывается постоянным.

Набросок различных процессов рассеяния, важных для закона Видемана – Франца.

^[3][4]

Ограничения теории

Эксперименты показали, что ценность L, хотя и является примерно постоянным, не является одинаковым для всех материалов. Киттель^[5] дает некоторые значения L начиная с L = 2.23×10⁻⁸ Вт Ом К⁻² для меди при температуре от 0 ° C до L = 3.2×10⁻⁸ Вт Ом К⁻² для вольфрама при 100 ° C. Розенберг^[6] отмечает, что закон Видемана – Франца обычно справедлив для высоких температур и для низких (т.е. несколько градусов Кельвина) температур, но может не выполняться при промежуточных температурах.

У многих металлов высокой чистоты и электрическая, и теплопроводность повышаются при понижении температуры. В некоторых материалах (например, серебро или же алюминий ), однако значение L также может уменьшаться с повышением температуры. В чистейших образцах серебра и при очень низких температурах L может упасть в 10 раз.^[7]

В вырожденные полупроводники число Лоренца L сильно зависит от некоторых параметров системы: размерности, силы межатомных взаимодействий и уровня Ферми. Этот закон не действует или значение числа Лоренца можно уменьшить, по крайней мере, в следующих случаях: манипулирование плотностью электронных состояний, изменение плотности легирования и толщины слоя в сверхрешетках и материалах с коррелированными носителями. В термоэлектрических материалах также есть поправки из-за граничных условий, в частности, разомкнутая цепь против замкнутой цепи. ^[8][9][10]

Нарушения

В 2011 г. N. Wakeham et al. установили, что соотношение теплопроводности и электрической холловской проводимости в металлической фазе квазиодномерного литий-молибденовый фиолетовый бронзовый Ли_0.9Пн₆О₁₇ расходится с понижением температуры, достигая значения на пять порядков больше, чем в обычных металлах, подчиняющихся закону Видемана – Франца.^[11][12] Это из-за спин-зарядовое разделение и ведет себя как Жидкость Латтинжера.^[11]

Исследование Ли, проведенное под руководством Беркли в 2016 году. и другие. также обнаружил большое нарушение закона Видемана – Франца вблизи перехода диэлектрик-металл в VO₂ нанопучки. В металлической фазе электронный вклад в теплопроводность был намного меньше, чем можно было бы ожидать из закона Видемана – Франца. Результаты можно объяснить с точки зрения независимого распространения заряда и тепла в сильно коррелированной системе.^[13][14]

Закон Видемана-Франца для молекул

В 2020 году Гален Крейвен и Авраам Ницан вывел закон Видемана-Франца для молекулярных систем, в которых в электронной проводимости доминирует не движение свободных электронов, как в металлах, а вместо этого перенос электронов между молекулярными сайтами.^[15] Молекулярный закон Видемана-Франца дается формулой

${ displaystyle { frac { kappa} { sigma}} = L _ { text {M}} { frac { lambda} {k _ { rm {B}}}}}$

куда

${ displaystyle L _ { text {M}} = { frac {1} {2}} left ({ frac {k _ { rm {B}}} {e}} right) ^ {2}}$

- число Лоренца для молекул и ${ displaystyle lambda}$ это реорганизационная энергия для электронного переноса.

Смотрите также

• Модель Друде

Рекомендации