Аддитивный белый гауссовский шум - Additive white Gaussian noise
Аддитивный белый гауссовский шум (AWGN) - базовая модель шума, используемая в теория информации имитировать влияние множества случайных процессов, происходящих в природе. Модификаторы обозначают конкретные характеристики:
- Добавка потому что он добавляется к любому шуму, который может быть присущ информационной системе.
- белый относится к идее, что он имеет равномерную мощность в полосе частот для информационной системы. Это аналогия белого цвета, который имеет однородное излучение на всех частотах в видимый спектр.
- Гауссовский потому что у него есть нормальное распределение во временной области со средним нулевым значением временной области.
Широкополосный шум возникает из многих естественных источников шума, таких как тепловые колебания атомов в проводниках (называемые тепловым шумом или Шум Джонсона – Найквиста ), дробовой шум, излучение черного тела от земли и других теплых предметов, а также от небесных источников, таких как Солнце. В Центральная предельная теорема из теория вероятности указывает на то, что суммирование многих случайных процессов будет иметь распределение, называемое гауссовым или нормальным.
AWGN часто используется как модель канала в котором единственным нарушением коммуникации является линейное добавление широкополосный или белый шум с постоянным спектральная плотность (выражается как Вт на герц из пропускная способность ) и Гауссово распределение амплитуды. Модель не учитывает угасание, частота избирательность, вмешательство, нелинейность или разброс. Тем не менее, он создает простые и понятные математические модели, которые полезны для понимания основного поведения системы до рассмотрения этих других явлений.
Канал AWGN - хорошая модель для многих спутниковое и каналы связи в дальнем космосе. Это не лучшая модель для большинства наземных линий связи из-за многолучевого распространения, блокировки местности, помех и т. Д. Однако для моделирования наземного пути AWGN обычно используется для моделирования фонового шума исследуемого канала в дополнение к многолучевости, блокировке местности и т. Д. помехи, помехи от земли и собственные помехи, с которыми современные радиосистемы сталкиваются при наземной эксплуатации.
Емкость канала
Канал AWGN представлен серией выходов в дискретном времени индекс события . это сумма ввода и шум, , куда является независимые и одинаково распределенные и взят из нулевого среднего нормальное распределение с отклонение (шум). В далее предполагается, что они не коррелируют с .
Пропускная способность канала бесконечна, если только шум отличен от нуля, а достаточно ограничены. Наиболее распространенным ограничением ввода является так называемое ограничение «мощности», требующее для кодового слова передаваемые по каналу, имеем:
куда представляет собой максимальную мощность канала. пропускная способность канала для канала с ограниченной мощностью определяется выражением:
Где это распределение . Развернуть , написав это в терминах дифференциальная энтропия:
Но и независимы, поэтому:
Оценка дифференциальная энтропия гауссиана дает:
Потому что и независимы и их сумма дает :
Из этой оценки мы получаем из свойства дифференциальной энтропии, что
Следовательно, пропускная способность канала определяется максимально достижимой границей взаимная информация:
Где максимизируется, когда:
Таким образом, пропускная способность канала для канала AWGN определяется как:
Пропускная способность канала и упаковка сфер
Предположим, что мы отправляем сообщения через канал с индексом от к , количество различных возможных сообщений. Если мы закодируем сообщения для бит, то определяем скорость в качестве:
Скорость называется достижимой, если существует последовательность кодов, так что максимальная вероятность ошибки стремится к нулю при приближается к бесконечности. Емкость это наивысшая достижимая скорость.
Рассмотрим кодовое слово длины отправлено по каналу AWGN с уровнем шума . При получении отклонение вектора кодового слова теперь равно , а его среднее значение - это отправленное кодовое слово. С большой вероятностью вектор содержится в сфере радиуса вокруг отправленного кодового слова. Если мы декодируем, отображая каждое полученное сообщение на кодовое слово в центре этой сферы, то ошибка возникает только тогда, когда полученный вектор находится за пределами этой сферы, что очень маловероятно.
С каждым вектором кодового слова связана сфера принятых векторов кодовых слов, которые декодируются в него, и каждая такая сфера должна однозначно отображаться на кодовое слово. Поскольку эти сферы не должны пересекаться, мы сталкиваемся с проблемой упаковка сфер. Сколько различных кодовых слов мы можем поместить в наш -битный вектор кодового слова? Полученные векторы имеют максимальную энергию и поэтому должен занимать сферу радиуса . Каждая сфера кодового слова имеет радиус . Объем п-мерная сфера прямо пропорциональна , поэтому максимальное количество однозначно декодируемых сфер, которые могут быть упакованы в нашу сферу с мощностью передачи P, равно:
Согласно этому аргументу, коэффициент R не может быть больше, чем .
Достижимость
В этом разделе мы показываем достижимость верхней границы ставки из последнего раздела.
Кодовая книга, известная как кодировщику, так и декодеру, генерируется путем выбора кодовых слов длины n, i.i.d. Гауссовский с дисперсией и означает ноль. Для большого n эмпирическая дисперсия кодовой книги будет очень близка к дисперсии ее распределения, тем самым избегая вероятностного нарушения ограничения мощности.
Принятые сообщения декодируются в сообщение в кодовой книге, которое является уникальным совместно типичным. Если такого сообщения нет или если ограничение мощности нарушено, объявляется ошибка декодирования.
Позволять обозначить кодовое слово для сообщения , в то время как есть, как и прежде полученный вектор. Определите следующие три события:
- Мероприятие : мощность полученного сообщения больше, чем .
- Мероприятие : переданные и принятые кодовые слова не являются типичными вместе.
- Мероприятие : в , то типовой набор куда , что означает, что неверное кодовое слово является типичным вместе с полученным вектором.
Поэтому возникает ошибка, если , или любой из происходят. По закону больших чисел стремится к нулю, когда n приближается к бесконечности, и по стыку Асимптотическая равнораспределенность то же самое относится к . Следовательно, при достаточно большом , обе и каждый меньше чем . С и независимы для у нас есть это и также независимы. Следовательно, совместным АЭП, . Это позволяет рассчитать , вероятность ошибки следующая:
Следовательно, как п приближается к бесконечности, идет к нулю и . Следовательно, существует код скорости R, произвольно близкий к мощности, полученной ранее.
Теорема кодирования обратная
Здесь мы показываем, что ставки выше пропускной способности недостижимы.
Предположим, что ограничение мощности удовлетворено для кодовой книги, и дополнительно предположим, что сообщения следуют равномерному распределению. Позволять быть входными сообщениями и выходные сообщения. Таким образом, информация течет как:
Используя Неравенство Фано дает:
куда так как
Позволять быть закодированным сообщением индекса кодового слова i. Потом:
Позволять - средняя мощность кодового слова индекса i:
Где сумма по всем входным сообщениям . и независимы, поэтому ожидание силы есть, для уровня шума :
И если нормально распространяется, мы имеем
Следовательно,
Мы можем применить равенство Дженсена к , вогнутая (нисходящая) функция Икс, получить:
Поскольку каждое кодовое слово индивидуально удовлетворяет ограничению мощности, среднее значение также удовлетворяет ограничению мощности. Следовательно,
Мы можем применить это, чтобы упростить неравенство выше и получить:
Следовательно, должно быть, что . Следовательно, R должно быть меньше значения, произвольно близкого к мощности, полученной ранее, поскольку .
Эффекты во временной области
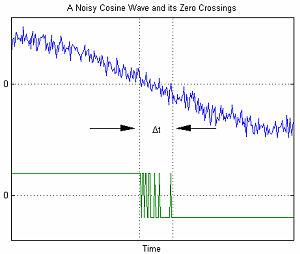
При последовательной передаче данных математическая модель AWGN используется для моделирования ошибки синхронизации, вызванной случайным дрожь (RJ).
На графике справа показан пример временных ошибок, связанных с AWGN. Переменная Δt представляет собой неопределенность перехода через нуль. По мере увеличения амплитуды AWGN соотношение сигнал шум уменьшается. Это приводит к увеличению неопределенности Δt.[1]
Под воздействием AWGN среднее количество переходов через нуль в положительную или отрицательную сторону в секунду на выходе узкополосного фильтра, когда на входе является синусоидальная волна, составляет:
Где
- ж0 = центральная частота фильтра
- B = ширина полосы фильтра
- SNR = отношение мощности сигнал / шум в линейном выражении
Эффекты в векторной области

В современных системах связи нельзя игнорировать AWGN с ограниченным диапазоном частот. При моделировании полосы пропускания AWGN в фазор области статистический анализ показывает, что амплитуды действительного и мнимого вкладов являются независимыми переменными, которые следуют Гауссово распределение модель. При объединении величина результирующего фазора равна Распределенный Рэлея случайная величина, а фаза равномерно распределена от 0 до 2π.
График справа показывает пример того, как AWGN с ограниченной полосой частот может влиять на сигнал когерентной несущей. Мгновенный отклик вектора шума невозможно точно предсказать, однако его усредненный по времени отклик можно предсказать статистически. Как показано на графике, мы уверенно прогнозируем, что вектор шума будет находиться внутри круга 1σ примерно 38% времени; вектор шума будет находиться внутри круга 2σ примерно 86% времени; а вектор шума будет находиться внутри круга 3σ около 98% времени.[1]












































































