Арифметическая иерархия - Arithmetical hierarchy

Иллюстрация того, как взаимодействуют уровни иерархии и где в ней находятся некоторые основные категории.

В математическая логика, то арифметическая иерархия, арифметическая иерархия или Клини –Мостовский иерархия классифицирует определенные наборы на основе сложность формул, которые их определяют. Любой набор, получивший классификацию, называется арифметический.

Арифметическая иерархия важна в теория рекурсии, эффективная дескриптивная теория множеств, а также изучение формальных теорий, таких как Арифметика Пеано.

В Алгоритм Тарского – Куратовского предоставляет простой способ получить верхнюю границу классификаций, присвоенных формуле и определенному набору.

В гиперарифметическая иерархия и аналитическая иерархия расширить арифметическую иерархию для классификации дополнительных формул и наборов.

Арифметическая иерархия формул

Арифметическая иерархия классифицирует формулы на языке арифметика первого порядка. Классификации обозначены ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ для натуральных чисел п (в том числе 0). Греческие буквы здесь Lightface символы, указывающие на то, что формулы не содержат заданных параметров.

Если формула ${ displaystyle phi}$ логически эквивалентна формуле только с ограниченные кванторы тогда ${ displaystyle phi}$ присвоена классификация ${ displaystyle Sigma _ {0} ^ {0}}$ и ${ displaystyle Pi _ {0} ^ {0}}$ .

Классификации ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ определяются индуктивно для каждого натурального числа п используя следующие правила:

Если ${ displaystyle phi}$ логически эквивалентно формуле вида ${ Displaystyle существует м_ {1} существует м_ {2} cdots существует м_ {к} psi}$ , где ${ displaystyle psi}$ является ${ Displaystyle Пи _ {п} ^ {0}}$ , тогда ${ displaystyle phi}$ присвоена классификация ${ Displaystyle Sigma _ {п + 1} ^ {0}}$ .
Если ${ displaystyle phi}$ логически эквивалентно формуле вида ${ Displaystyle forall m_ {1} forall m_ {2} cdots forall m_ {k} psi}$ , где ${ displaystyle psi}$ является ${ displaystyle Sigma _ {n} ^ {0}}$ , тогда ${ displaystyle phi}$ присвоена классификация ${ Displaystyle Пи _ {п + 1} ^ {0}}$ .

Также ${ displaystyle Sigma _ {n} ^ {0}}$ формула эквивалентна формуле, которая начинается с некоторого экзистенциальные кванторы и чередует ${ displaystyle n-1}$ раз между сериями экзистенциальных и универсальные кванторы; в то время как ${ Displaystyle Пи _ {п} ^ {0}}$ формула эквивалентна формуле, которая начинается с некоторых универсальных кванторов и чередуется аналогичным образом.

Поскольку каждая формула эквивалентна формуле в пренекс нормальная форма каждой формуле без заданных кванторов присваивается хотя бы одна классификация. Поскольку избыточные квантификаторы могут быть добавлены к любой формуле, как только формуле присвоена классификация ${ displaystyle Sigma _ {n} ^ {0}}$ или ${ Displaystyle Пи _ {п} ^ {0}}$ ему будут присвоены классификации ${ displaystyle Sigma _ {r} ^ {0}}$ и ${ displaystyle Pi _ {r} ^ {0}}$ для каждого р лучше чем п. Таким образом, наиболее важной классификацией формулы является класс с наименьшим п, потому что этого достаточно для определения всех остальных классификаций.

Арифметическая иерархия множеств натуральных чисел

Множество Икс натуральных чисел определяется формулой φ на языке Арифметика Пеано (язык первого порядка с символами «0» для нуля, «S» для функции-преемника, «+» для сложения, «×» для умножения и «=» для равенства), если элементы Икс - это в точности числа, удовлетворяющие φ. То есть для всех натуральных чисел п,

{ displaystyle n in X Leftrightarrow mathbb {N} models varphi ({ underline {n}}),}

где ${ displaystyle { underline {n}}}$ это число на языке арифметики, соответствующее ${ displaystyle n}$ . Множество определимо в арифметике первого порядка, если оно определено некоторой формулой на языке арифметики Пеано.

Каждый набор Икс натуральных чисел, которая определима в арифметике первого порядка, получает классификацию вида ${ displaystyle Sigma _ {n} ^ {0}}$ , ${ Displaystyle Пи _ {п} ^ {0}}$ , и ${ displaystyle Delta _ {n} ^ {0}}$ , где ${ displaystyle n}$ является натуральным числом следующим образом. Если Икс определяется ${ displaystyle Sigma _ {n} ^ {0}}$ формула тогда Икс присвоена классификация ${ displaystyle Sigma _ {n} ^ {0}}$ . Если Икс определяется ${ Displaystyle Пи _ {п} ^ {0}}$ формула тогда Икс присвоена классификация ${ Displaystyle Пи _ {п} ^ {0}}$ . Если Икс оба ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ тогда ${ displaystyle X}$ присвоена дополнительная классификация ${ displaystyle Delta _ {n} ^ {0}}$ .

Обратите внимание, что редко имеет смысл говорить о ${ displaystyle Delta _ {n} ^ {0}}$ формулы; первый квантор формулы либо экзистенциальный, либо универсальный. Так что ${ displaystyle Delta _ {n} ^ {0}}$ набор не определяется ${ displaystyle Delta _ {n} ^ {0}}$ формула; скорее, есть оба ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ формулы, определяющие множество.

Параллельное определение используется для определения арифметической иерархии на конечных Декартовы степени множества натуральных чисел. Вместо формул с одной свободной переменной, формулы с k свободные числовые переменные используются для определения арифметической иерархии на наборах k-кортежи натуральных чисел. На самом деле они связаны с использованием функция сопряжения.

Релятивизированные арифметические иерархии

Так же, как мы можем определить, что это значит для набора Икс быть рекурсивный относительно другого набора Y позволяя вычислению определять Икс консультироваться Y как оракул мы можем расширить это понятие на всю арифметическую иерархию и определить, что оно означает для Икс быть ${ displaystyle Sigma _ {n} ^ {0}}$ , ${ displaystyle Delta _ {n} ^ {0}}$ или ${ Displaystyle Пи _ {п} ^ {0}}$ в Y, обозначаемые соответственно ${ displaystyle Sigma _ {n} ^ {0, Y}}$ ${ displaystyle Delta _ {n} ^ {0, Y}}$ и ${ displaystyle Pi _ {n} ^ {0, Y}}$ . Для этого зафиксируйте набор целых чисел Y и добавить предикат для членства в Y на язык арифметики Пеано. Затем мы говорим, что Икс в ${ displaystyle Sigma _ {n} ^ {0, Y}}$ если он определяется ${ displaystyle Sigma _ {n} ^ {0}}$ формула на этом расширенном языке. Другими словами, Икс является ${ displaystyle Sigma _ {n} ^ {0, Y}}$ если он определяется ${ displaystyle Sigma _ {n} ^ {0}}$ формула позволяла задавать вопросы о членстве в Y. В качестве альтернативы можно просмотреть ${ displaystyle Sigma _ {n} ^ {0, Y}}$ наборы как те наборы, которые могут быть построены, начиная с наборов, рекурсивных в Y и поочередно принимая союзы и перекрестки из этих наборов до п раз.

Например, пусть Y быть набором целых чисел. Позволять Икс - множество чисел, делящихся на элемент Y. Тогда Икс определяется формулой ${ Displaystyle фи (п) = существует м существует т (Y (м) земля м раз т = п)}$ так Икс в ${ displaystyle Sigma _ {1} ^ {0, Y}}$ (на самом деле это в ${ displaystyle Delta _ {0} ^ {0, Y}}$ также, поскольку мы могли связать оба квантора числом n).

Арифметическая сводимость и степени

Арифметическая сводимость - промежуточное понятие между Сводимость по Тьюрингу и гиперарифметическая сводимость.

Набор есть арифметический (также арифметика и арифметически определяемый), если он определен некоторой формулой на языке арифметики Пеано. Эквивалентно Икс является арифметическим, если Икс является ${ displaystyle Sigma _ {n} ^ {0}}$ или ${ Displaystyle Пи _ {п} ^ {0}}$ для некоторого целого числа п. Множество Икс является арифметическим в множество Y, обозначенный ${ Displaystyle X leq _ {A} Y}$ , если Икс определима как некоторая формула на языке арифметики Пеано, расширенная предикатом для принадлежности к Y. Эквивалентно, Икс является арифметическим в Y если Икс в ${ displaystyle Sigma _ {n} ^ {0, Y}}$ или ${ displaystyle Pi _ {n} ^ {0, Y}}$ для некоторого целого числа п. Синоним для ${ Displaystyle X leq _ {A} Y}$ является: Икс является арифметически сводимый к Y.

Соотношение ${ Displaystyle X leq _ {A} Y}$ рефлексивно и транзитивно, поэтому отношение ${ Displaystyle Equiv _ {A}}$ определяется правилом

{ Displaystyle X Equiv _ {A} Y Leftrightarrow X leq _ {A} Y land Y leq _ {A} X}

является отношением эквивалентности. Классы эквивалентности этого отношения называются арифметические степени; они частично заказаны под ${ displaystyle leq _ {A}}$ .

Арифметическая иерархия подмножеств пространства Кантора и Бэра

В Канторовское пространство, обозначенный ${ displaystyle 2 ^ { omega}}$ , - множество всех бесконечных последовательностей нулей и единиц; то Пространство Бэра, обозначенный ${ displaystyle omega ^ { omega}}$ или ${ Displaystyle { mathcal {N}}}$ , - множество всех бесконечных последовательностей натуральных чисел. Обратите внимание, что элементы пространства Кантора можно отождествить с наборами целых чисел, а элементы пространства Бэра - с функциями от целых чисел до целых.

Обычная аксиоматизация арифметика второго порядка использует язык, основанный на множествах, в котором квантификаторы множеств, естественно, могут рассматриваться как количественные в пространстве Кантора. Подмножеству пространства Кантора присваивается классификация ${ displaystyle Sigma _ {n} ^ {0}}$ если это определяется ${ displaystyle Sigma _ {n} ^ {0}}$ формула. Набору присвоена классификация ${ Displaystyle Пи _ {п} ^ {0}}$ если это определяется ${ Displaystyle Пи _ {п} ^ {0}}$ формула. Если набор оба ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ затем дается дополнительная классификация ${ displaystyle Delta _ {n} ^ {0}}$ . Например, пусть ${ displaystyle O subset 2 ^ { omega}}$ быть набором всех бесконечных двоичных строк, которые не все 0 (или, что эквивалентно, набор всех непустых наборов целых чисел). В качестве ${ Displaystyle O = {X in 2 ^ { omega} | существует n (X (n) = 1) }}$ Мы видим, что ${ displaystyle O}$ определяется ${ displaystyle Sigma _ {1} ^ {0}}$ формула и, следовательно, является ${ displaystyle Sigma _ {1} ^ {0}}$ набор.

Обратите внимание, что хотя элементы пространства Кантора (рассматриваемые как наборы целых чисел) и подмножества пространства Кантора классифицируются в арифметических иерархиях, это не одна и та же иерархия. На самом деле отношения между двумя иерархиями интересны и нетривиальны. Например, ${ Displaystyle Пи _ {п} ^ {0}}$ элементы пространства Кантора (в общем случае) не совпадают с элементами ${ displaystyle X}$ пространства Кантора так, чтобы ${ displaystyle {X }}$ это ${ Displaystyle Пи _ {п} ^ {0}}$ подмножество пространства Кантора. Однако есть много интересных результатов, касающихся двух иерархий.

Существует два способа классификации подмножества пространства Бэра в арифметической иерархии.

Подмножество пространства Бэра имеет соответствующее подмножество пространства Кантора под картой, которая принимает каждую функцию из ${ displaystyle omega}$ к ${ displaystyle omega}$ к характеристическая функция его графика. Подмножеству пространства Бэра дается классификация ${ Displaystyle Sigma _ {п} ^ {1}}$ , ${ Displaystyle Пи _ {п} ^ {1}}$ , или же ${ displaystyle Delta _ {n} ^ {1}}$ тогда и только тогда, когда соответствующее подмножество канторовского пространства имеет ту же классификацию.
Эквивалентное определение аналитической иерархии в пространстве Бэра дается путем определения аналитической иерархии формул с использованием функциональной версии арифметики второго порядка; тогда аналитическая иерархия на подмножествах пространства Кантора может быть определена из иерархии на пространстве Бэра. Это альтернативное определение дает точно такие же классификации, как и первое определение.

Параллельное определение используется для определения арифметической иерархии конечных декартовых степеней пространства Бэра или пространства Кантора с использованием формул с несколькими свободными переменными. Арифметическая иерархия может быть определена на любом эффективное польское пространство; определение особенно просто для пространств Кантора и Бэра, потому что они соответствуют языку обычной арифметики второго порядка.

Обратите внимание, что мы также можем определить арифметическую иерархию подмножеств пространств Кантора и Бэра относительно некоторого набора целых чисел. На самом деле жирный шрифт ${ Displaystyle mathbf { Sigma} _ {п} ^ {0}}$ это просто союз ${ displaystyle Sigma _ {n} ^ {0, Y}}$ для всех наборов целых чисел Y. Обратите внимание, что иерархия жирным шрифтом - это просто стандартная иерархия Наборы Бореля.

Расширения и вариации

Можно определить арифметическую иерархию формул, используя язык, расширенный функциональным символом для каждого примитивная рекурсивная функция. Этот вариант немного меняет классификацию ${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0}}$ , поскольку использование примитивных рекурсивных функций в арифметике Пеано первого порядка требует, в общем, неограниченного экзистенциального квантора, и, следовательно, некоторых наборов, которые находятся в ${ displaystyle Sigma _ {0} ^ {0}}$ по этому определению находятся в ${ displaystyle Sigma _ {1} ^ {0}}$ по определению, данному в начале статьи. ${ displaystyle Sigma _ {1} ^ {0}}$ и, таким образом, все более высокие классы в иерархии остаются неизменными.

Более семантическая вариация иерархии может быть определена для всех конечных отношений натуральных чисел; используется следующее определение. Каждое вычислимое отношение определяется как ${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0}}$ . Классификации ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ определяются индуктивно по следующим правилам.

Если отношение ${ Displaystyle R (п_ {1}, ldots, n_ {l}, m_ {1}, ldots, m_ {k}) ,}$ является ${ displaystyle Sigma _ {n} ^ {0}}$ тогда отношение ${ Displaystyle S (n_ {1}, ldots, n_ {l}) = forall m_ {1} cdots forall m_ {k} R (n_ {1}, ldots, n_ {l}, m_ { 1}, ldots, m_ {k})}$ определяется как ${ Displaystyle Пи _ {п + 1} ^ {0}}$
Если отношение ${ Displaystyle R (п_ {1}, ldots, n_ {l}, m_ {1}, ldots, m_ {k}) ,}$ является ${ Displaystyle Пи _ {п} ^ {0}}$ тогда отношение ${ Displaystyle S (п_ {1}, ldots, n_ {l}) = существует m_ {1} cdots exists m_ {k} R (n_ {1}, ldots, n_ {l}, m_ { 1}, ldots, m_ {k})}$ определяется как ${ Displaystyle Sigma _ {п + 1} ^ {0}}$

Этот вариант немного меняет классификацию некоторых наборов. Особенно, ${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0}}$ , как класс множеств (определяемых отношениями в классе), идентичен ${ displaystyle Delta _ {1} ^ {0}}$ как последний был ранее определен. Его можно расширить, чтобы охватить финитарные отношения в натуральных числах, пространстве Бэра и пространстве Кантора.

Значение обозначений

Обозначению арифметической иерархии в формулах можно придать следующие значения.

Нижний индекс ${ displaystyle n}$ в символах ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ указывает количество чередований блоков кванторов универсальных и экзистенциальных чисел, используемых в формуле. Более того, самый внешний блок экзистенциальный в ${ displaystyle Sigma _ {n} ^ {0}}$ формулы и универсальные в ${ Displaystyle Пи _ {п} ^ {0}}$ формулы.

Верхний индекс ${ displaystyle 0}$ в символах ${ displaystyle Sigma _ {n} ^ {0}}$ , ${ Displaystyle Пи _ {п} ^ {0}}$ , и ${ displaystyle Delta _ {n} ^ {0}}$ указывает тип объектов, по которым проводится количественная оценка. Объекты типа 0 - это натуральные числа, а объекты типа ${ displaystyle i + 1}$ - это функции, отображающие набор объектов типа ${ displaystyle i}$ к натуральным числам. Количественная оценка объектов более высокого типа, таких как функции от натуральных чисел к натуральным числам, описывается надстрочным индексом больше 0, как в аналитическая иерархия. Верхний индекс 0 указывает кванторы над числами, верхний индекс 1 будет указывать количественную оценку функций от чисел к числам (объекты типа 1), верхний индекс 2 будет соответствовать количественной оценке функций, которые принимают объект типа 1 и возвращают число, и так далее.

Примеры

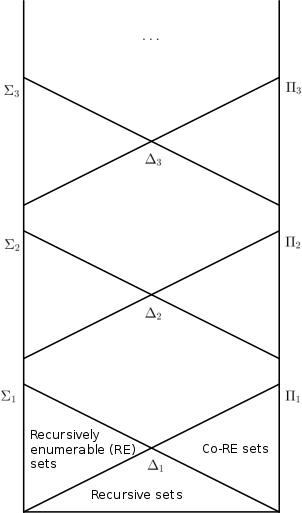
В ${ displaystyle Sigma _ {1} ^ {0}}$ наборы чисел - те, которые могут быть определены формулой вида ${ Displaystyle существует n_ {1} cdots exists n_ {k} psi (n_ {1}, ldots, n_ {k}, m)}$ где ${ displaystyle psi}$ имеет только ограниченные кванторы. Это именно те рекурсивно перечислимые множества.
Набор натуральных чисел, являющихся индексами машин Тьюринга, вычисляющих общие функции, равен ${ displaystyle Pi _ {2} ^ {0}}$ . Интуитивно понятно, что индекс ${ displaystyle e}$ попадает в это множество тогда и только тогда, когда для каждого ${ displaystyle m}$ "существует ${ displaystyle s}$ так что машина Тьюринга с индексом ${ displaystyle e}$ останавливается при вводе ${ displaystyle m}$ после ${ displaystyle s}$ шаги ». Полное доказательство показало бы, что свойство, указанное в кавычках в предыдущем предложении, может быть определено на языке арифметики Пеано с помощью ${ displaystyle Sigma _ {1} ^ {0}}$ формула.
Каждые ${ displaystyle Sigma _ {1} ^ {0}}$ подмножество пространства Бэра или пространства Кантора является открытым множеством в обычной топологии на пространстве. Более того, для любого такого множества существует вычислимая нумерация гёделевских чисел основных открытых множеств, объединение которых является исходным множеством. Именно по этой причине, ${ displaystyle Sigma _ {1} ^ {0}}$ наборы иногда называют эффективно открыть. Точно так же каждый ${ displaystyle Pi _ {1} ^ {0}}$ набор закрыт и ${ displaystyle Pi _ {1} ^ {0}}$ наборы иногда называют эффективно закрыто.
Каждое арифметическое подмножество пространства Кантора или пространства Бэра является Набор Бореля. Иерархия Lightface Borel расширяет арифметическую иерархию, включая дополнительные наборы Borel. Например, каждый ${ displaystyle Pi _ {2} ^ {0}}$ подмножеством пространства Кантора или Бэра является ${ displaystyle G _ { delta}}$ набор (то есть набор, который равен пересечению счетного числа открытых множеств). Более того, каждое из этих открытых множеств ${ displaystyle Sigma _ {1} ^ {0}}$ и список гёделевских чисел этих открытых множеств имеет вычислимое перечисление. Если ${ Displaystyle фи (Х, п, м)}$ это ${ displaystyle Sigma _ {0} ^ {0}}$ формула со свободным набором переменной Икс и свободные числовые переменные ${ displaystyle n, m}$ затем ${ displaystyle Pi _ {2} ^ {0}}$ набор ${ displaystyle {X mid forall n существует m phi (X, n, m) }}$ это пересечение ${ displaystyle Sigma _ {1} ^ {0}}$ наборы формы ${ Displaystyle {Икс середина существует м фи (Х, п, м) }}$ так как п колеблется в наборе натуральных чисел.
В ${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0}}$ формулы можно проверить, просматривая все случаи один за другим, что возможно, потому что все их кванторы ограничены. Время для этого полиномиально по их аргументам (например, полиномиально от п за ${ Displaystyle varphi (п)}$ ); таким образом их соответствующие проблемы решения включены в E (так как п экспоненциально по количеству битов). Это больше не выполняется при альтернативных определениях ${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0}}$ , которые позволяют использовать примитивные рекурсивные функции, поскольку теперь кванторы могут быть связаны любой примитивно рекурсивной функцией аргументов.
В ${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0}}$ формулы с альтернативным определением, которое позволяет использовать примитивно рекурсивные функции с ограниченными кванторами, соответствуют наборам целых чисел вида ${ Displaystyle {п: е (п) = 0 }}$ для примитивной рекурсивной функции ж. Это потому, что разрешение ограниченного квантора ничего не добавляет к определению: для примитивно рекурсивного ж, ${ displaystyle forall k$ такой же как ${ Displaystyle f (0) + f (1) + ... f (n) = 0}$ , и ${ Displaystyle существует к$ такой же как ${ Displaystyle f (0) * f (1) * ... f (n) = 0}$ ; с рекурсия курса ценностей каждый из них может быть определен одной простой функцией рекурсии.

Характеристики

Следующие свойства имеют место для арифметической иерархии множеств натуральных чисел и арифметической иерархии подмножеств пространства Кантора или Бэра.

Коллекции ${ Displaystyle Пи _ {п} ^ {0}}$ и ${ displaystyle Sigma _ {n} ^ {0}}$ замкнуты относительно конечных союзы и конечный перекрестки соответствующих элементов.
Набор есть ${ displaystyle Sigma _ {n} ^ {0}}$ тогда и только тогда, когда его дополнение ${ Displaystyle Пи _ {п} ^ {0}}$ . Набор есть ${ displaystyle Delta _ {n} ^ {0}}$ тогда и только тогда, когда набор одновременно ${ displaystyle Sigma _ {n} ^ {0}}$ и ${ Displaystyle Пи _ {п} ^ {0}}$ , в этом случае его дополнение также будет ${ displaystyle Delta _ {n} ^ {0}}$ .
Включения ${ Displaystyle Пи _ {п} ^ {0} subsetneq Пи _ {п + 1} ^ {0}}$ и ${ Displaystyle Sigma _ {п} ^ {0} subsetneq Sigma _ {п + 1} ^ {0}}$ держать для всех ${ displaystyle n}$ . Таким образом иерархия не разрушается. Это прямое следствие Теорема Поста.
Включения ${ displaystyle Delta _ {n} ^ {0} subsetneq Pi _ {n} ^ {0}}$ , ${ Displaystyle Delta _ {n} ^ {0} subsetneq Sigma _ {n} ^ {0}}$ и ${ displaystyle Sigma _ {n} ^ {0} cup Pi _ {n} ^ {0} subsetneq Delta _ {n + 1} ^ {0}}$ держаться за ${ Displaystyle п geq 1}$ .

Например, для универсальной машины Тьюринга T набор пар (n, m) таких, что T останавливается на n, но не на m, находится в ${ displaystyle Delta _ {2} ^ {0}}$ (вычисляемый с помощью оракула для решения проблемы остановки), но не в ${ displaystyle Sigma _ {1} ^ {0} cup Pi _ {1} ^ {0}}$ , .
${ Displaystyle Sigma _ {0} ^ {0} = Pi _ {0} ^ {0} = Delta _ {0} ^ {0} = Sigma _ {0} ^ {0} cup Pi _ {0} ^ {0} subset Delta _ {1} ^ {0}}$ . Включение строго по определению, данному в этой статье, но тождество с ${ displaystyle Delta _ {1} ^ {0}}$ выполняется при одном из вариантов определения приведено выше.

Отношение к машинам Тьюринга

Вычислимые множества

Если S является Вычислимое множество Тьюринга, то и S, и его дополнять рекурсивно перечислимы (если T - машина Тьюринга, дающая 1 для входных данных в S и 0, в противном случае мы можем построить машину Тьюринга, останавливающуюся только на первом, а другую - только на втором).

К Теорема Поста, и S, и его дополнение лежат в ${ displaystyle Sigma _ {1} ^ {0}}$ . Это означает, что S находится как в ${ displaystyle Sigma _ {1} ^ {0}}$ И в ${ displaystyle Pi _ {1} ^ {0}}$ , а значит, и в ${ displaystyle Delta _ {1} ^ {0}}$ .

Аналогично для любого множества S из ${ displaystyle Delta _ {1} ^ {0}}$ , и S, и его дополнение лежат в ${ displaystyle Sigma _ {1} ^ {0}}$ и поэтому (по Теорема Поста ), рекурсивно перечислимые некоторыми машинами Тьюринга T₁ и т₂, соответственно. Для каждого числа n ровно одна из этих остановок. Следовательно, мы можем построить машину Тьюринга T, которая чередуется между T₁ и т₂, останавливая и возвращая 1, когда первый останавливается, или останавливается и возвращает 0, когда последний останавливается. Таким образом, T останавливается на каждом n и возвращает, находится ли он в S, поэтому S вычислим.

Резюме основных результатов

Вычислимые по Тьюрингу множества натуральных чисел - это в точности множества на уровне ${ displaystyle Delta _ {1} ^ {0}}$ арифметической иерархии. Рекурсивно перечислимые множества - это в точности множества на уровне ${ displaystyle Sigma _ {1} ^ {0}}$ .

Нет машина оракула способна решать свои собственные проблема остановки (применяется вариант доказательства Тьюринга). Проблема остановки для ${ displaystyle Delta _ {n} ^ {0, Y}}$ оракул фактически сидит в ${ displaystyle Sigma _ {n + 1} ^ {0, Y}}$ .

Теорема Поста устанавливает тесную связь между арифметической иерархией множеств натуральных чисел и Степени Тьюринга. В частности, он устанавливает следующие факты для всех п ≥ 1:

Набор ${ Displaystyle emptyset ^ {(п)}}$ (в пth Прыжок Тьюринга пустого множества) много-один полный в ${ displaystyle Sigma _ {n} ^ {0}}$ .
Набор ${ Displaystyle mathbb {N} setminus emptyset ^ {(п)}}$ много-одно полное в ${ Displaystyle Пи _ {п} ^ {0}}$ .
Набор ${ Displaystyle emptyset ^ {(п-1)}}$ является Тьюринг завершен в ${ displaystyle Delta _ {n} ^ {0}}$ .

В полиномиальная иерархия представляет собой «допустимую с ограниченными ресурсами» версию арифметической иерархии, в которой для задействованных чисел ставятся границы полиномиальной длины (или, что то же самое, границы полиномиального времени устанавливаются на задействованных машинах Тьюринга). Он дает более точную классификацию некоторых наборов натуральных чисел, находящихся на уровне ${ displaystyle Delta _ {1} ^ {0}}$ арифметической иерархии.

Отношение к другим иерархиям

Lightface		Жирный шрифт
Σ⁰ ₀ = Π⁰ ₀ = Δ⁰ ₀ (иногда то же самое, что Δ⁰ ₁)		Σ⁰ ₀ = Π⁰ ₀ = Δ⁰ ₀ (если определено)
Δ⁰ ₁ = рекурсивный		Δ⁰ ₁ = прищемить
Σ⁰ ₁ = рекурсивно перечислимый	Π⁰ ₁ = ко-рекурсивно перечислимый	Σ⁰ ₁ = г = открыто	Π⁰ ₁ = F = закрыто
Δ⁰ ₂		Δ⁰ ₂
Σ⁰ ₂	Π⁰ ₂	Σ⁰ ₂ = F_σ	Π⁰ ₂ = г_δ
Δ⁰ ₃		Δ⁰ ₃
Σ⁰ ₃	Π⁰ ₃	Σ⁰ ₃ = г_δσ	Π⁰ ₃ = F_σδ
⋮		⋮
Σ⁰ _<ω = Π⁰ _<ω = Δ⁰ _<ω = Σ¹ ₀ = Π¹ ₀ = Δ¹ ₀ = арифметический		Σ⁰ _<ω = Π⁰ _<ω = Δ⁰ _<ω = Σ¹ ₀ = Π¹ ₀ = Δ¹ ₀ = жирный арифметический
⋮		⋮
Δ⁰ _α (α рекурсивный )		Δ⁰ _α (α счетный )
Σ⁰ _α	Π⁰ _α	Σ⁰ _α	Π⁰ _α
⋮		⋮
Σ⁰ _ω^СК ₁ = Π⁰ _ω^СК ₁ = Δ⁰ _ω^СК ₁ = Δ¹ ₁ = гиперарифметический		Σ⁰ _ω₁ = Π⁰ _ω₁ = Δ⁰ _ω₁ = Δ¹ ₁ = B = Борель
Σ¹ ₁ = лайтфейс аналитический	Π¹ ₁ = световой коаналитический	Σ¹ ₁ = А = аналитический	Π¹ ₁ = CA = коаналитический
Δ¹ ₂		Δ¹ ₂
Σ¹ ₂	Π¹ ₂	Σ¹ ₂ = PCA	Π¹ ₂ = CPCA
Δ¹ ₃		Δ¹ ₃
Σ¹ ₃	Π¹ ₃	Σ¹ ₃ = PCPCA	Π¹ ₃ = CPCPCA
⋮		⋮
Σ¹ _<ω = Π¹ _<ω = Δ¹ _<ω = Σ² ₀ = Π² ₀ = Δ² ₀ = аналитический		Σ¹ _<ω = Π¹ _<ω = Δ¹ _<ω = Σ² ₀ = Π² ₀ = Δ² ₀ = п = проективный
⋮		⋮

Важный классы сложности (более )
Считается выполнимым	DLOGTIME AC⁰ АКК⁰ TC⁰ L SL RL NL NC SC CC п P-полный ЗПП RP BPP BQP APX
Подозревается в невозможности	ВВЕРХ НП НП-полный NP-жесткий со-НП совместно NP-полный AM QMA PH ⊕P PP #П # P-complete IP PSPACE PSPACE-полный
Считается невозможным	EXPTIME NEXPTIME EXPSPACE 2-EXPTIME НАЧАЛЬНЫЙ PR р RE ВСЕ
Иерархии классов	Полиномиальная иерархия Экспоненциальная иерархия Иерархия Гжегорчика Арифметическая иерархия Логическая иерархия
Семьи классов	DTIME NTIME DSPACE NSPACE Вероятностно проверяемое доказательство Интерактивная система доказательств