Координатный спуск - Coordinate descent

Координатный спуск является алгоритм оптимизации который последовательно минимизирует по координатным направлениям, чтобы найти минимум функции. На каждой итерации алгоритм определяет координировать или координатный блок с помощью правила выбора координат, затем точно или неточно минимизирует по соответствующей координатной гиперплоскости, фиксируя все другие координаты или координатные блоки. А линейный поиск вдоль координировать Направление может выполняться на текущей итерации, чтобы определить соответствующий размер шага. Координатный спуск применим как в дифференцируемом, так и в свободном от производных контекстах.

Описание

Координатный спуск основан на идее, что минимизация функции многих переменных может быть достигнута путем минимизации его в одном направлении за раз, то есть путем решения одномерных (или, по крайней мере, гораздо более простых) задач оптимизации в цикле.[1] В простейшем случае циклический координатный спуск, один циклически перебирает направления по одному, минимизируя целевую функцию по каждому направлению координат за раз. То есть начиная с начальных значений переменных

,

круглый определяет из путем итеративного решения задач оптимизации с одной переменной

[2]

для каждой переменной из , за от 1 до .

Таким образом, мы начинаем с первоначального предположения. за местный минимум , и получает последовательность итеративно.

При выполнении линейный поиск на каждой итерации автоматически

Можно показать, что эта последовательность имеет те же свойства сходимости, что и наискорейший спуск. Нет улучшения после одного цикла линейный поиск вдоль координатных направлений подразумевает достижение стационарной точки.

Этот процесс проиллюстрирован ниже.

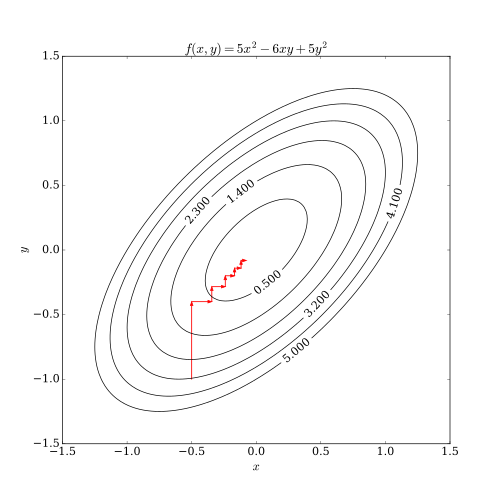
Координатный descent.svg

Отличительный случай

В случае непрерывно дифференцируемый функция F, алгоритм координатного спуска может быть набросал в качестве:[1]

  • Выберите начальный вектор параметров Икс.
  • Пока не будет достигнута сходимость или для некоторого фиксированного количества итераций:
    • Выберите индекс я из 1 к п.
    • Выберите размер шага α.
    • Обновлять Икся к Икся − α∂F/∂Икся(Икс).

Размер шага можно выбирать разными способами, например, решая точный минимизатор ж(Икся) = F(Икс) (т.е. F со всеми переменными, кроме Икся фиксировано) или по традиционным критериям поиска по строкам.[1]

Ограничения

Координатный спуск имеет две проблемы. Один из них не-гладкий многопараметрическая функция. На следующем рисунке показано, что итерация спуска координат может застрять на не-стационарный пункт если кривые уровня функции не гладкие. Предположим, что алгоритм находится в точке (-2, -2); тогда есть два выровненных по оси направления, которые он может рассмотреть для шага, обозначенных красными стрелками. Однако каждый шаг в этих двух направлениях будет увеличивать значение целевой функции (предполагая задачу минимизации), поэтому алгоритм не будет предпринимать никаких шагов, даже если оба шага вместе приблизят алгоритм к оптимальному. Хотя этот пример показывает, что спуск координат не обязательно сходится к оптимуму, можно показать формальную сходимость при разумных условиях.[3]

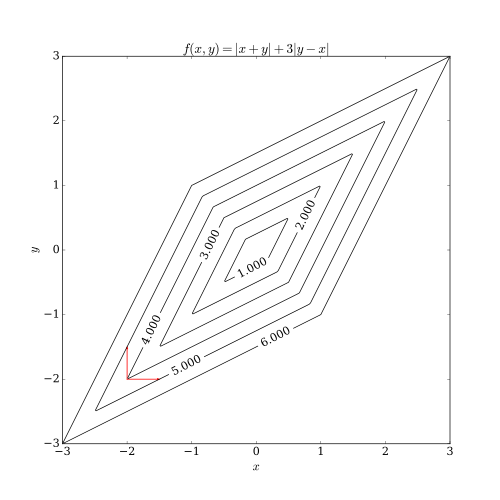
Негладкий координатный descent.svg

Другая проблема - сложность параллелизма. Поскольку природа спуска координат заключается в циклическом перемещении по направлениям и минимизации целевой функции по каждому направлению координат, спуск координат не является очевидным кандидатом на массовый параллелизм. Недавние исследования показали, что массивный параллелизм применим к координатному спуску, ослабляя изменение целевой функции по каждому направлению координат.[4][5][6]

Приложения

Алгоритмы координатного спуска популярны среди практиков благодаря своей простоте, но это же свойство привело к тому, что исследователи оптимизации в значительной степени игнорировали их в пользу более интересных (сложных) методов.[1] Одно из первых применений оптимизации спуска координат было в области компьютерной томографии.[7] где была обнаружена быстрая сходимость[8] и впоследствии был использован для клинической реконструкции КТ с несколькими срезами.[9] Более того, интерес к использованию координатного спуска возрос с появлением крупномасштабных задач в машинное обучение, где координатный спуск оказался конкурентоспособным по сравнению с другими методами при применении к таким задачам, как обучение линейных опорные векторные машины[10] (видеть LIBLINEAR ) и неотрицательная матричная факторизация.[11] Они привлекательны для задач, где вычисление градиентов невозможно, возможно, потому, что данные, необходимые для этого, распределены по компьютерным сетям.[12]

Смотрите также

Рекомендации

  1. ^ а б c d Райт, Стивен Дж. (2015). «Алгоритмы координатного спуска». Математическое программирование. 151 (1): 3–34. arXiv:1502.04759. Дои:10.1007 / s10107-015-0892-3.
  2. ^ https://www.cs.cmu.edu/~ggordon/10725-F12/slides/25-coord-desc.pdf
  3. ^ Сполл, Дж. К. (2012). «Циклический процесс качелей для оптимизации и идентификации». Журнал теории оптимизации и приложений. 154 (1): 187–208. Дои:10.1007 / s10957-012-0001-1.
  4. ^ Zheng, J .; Saquib, S. S .; Sauer, K .; Боуман, К. А. (2000-10-01). «Параллелизуемые байесовские алгоритмы томографии с быстрой гарантированной сходимостью». IEEE Transactions по обработке изображений. 9 (10): 1745–1759. Bibcode:2000ITIP .... 9.1745Z. CiteSeerX  10.1.1.34.4282. Дои:10.1109/83.869186. ISSN  1057-7149. PMID  18262913.
  5. ^ Фесслер, Дж. А .; Ficaro, E.P .; Clinthorne, N.H .; Ланге, К. (1997-04-01). "Алгоритмы восхождения сгруппированных координат для восстановления изображения передачи с штрафной вероятностью". IEEE Transactions on Medical Imaging. 16 (2): 166–175. Дои:10.1109/42.563662. HDL:2027.42/86021. ISSN  0278-0062. PMID  9101326.
  6. ^ Ван, Сяо; Сабне, Амит; Киснер, Шерман; Рагхунатан, Ананд; Боуман, Шарль; Мидкифф, Сэмюэл (01.01.2016). Высокопроизводительная реконструкция изображения на основе модели. Материалы 21-го симпозиума ACM SIGPLAN по принципам и практике параллельного программирования. ППоПП '16. Нью-Йорк, Нью-Йорк, США: ACM. С. 2: 1–2: 12. Дои:10.1145/2851141.2851163. ISBN  9781450340922.
  7. ^ Зауэр, Кен; Боуман, Чарльз (февраль 1993 г.). «Стратегия локального обновления для итеративной реконструкции из прогнозов» (PDF). Транзакции IEEE при обработке сигналов. 41 (2): 534–548. Bibcode:1993ITSP ... 41..534S. CiteSeerX  10.1.1.135.6045. Дои:10.1109/78.193196.
  8. ^ Ю, Чжоу; Тибо, Жан-Батист; Боуман, Шарль; Зауэр, Кен; Се, Цзян (январь 2011 г.). «Быстрая реконструкция рентгеновской компьютерной томографии на основе модели с использованием пространственно неоднородной оптимизации ИКД» (PDF). IEEE Transactions по обработке изображений. 20 (1): 161–175. Bibcode:2011ITIP ... 20..161л. Дои:10.1109 / TIP.2010.2058811. PMID  20643609.
  9. ^ Тибо, Жан-Батист; Зауэр, Кен; Боуман, Шарль; Се, Цзян (ноябрь 2007 г.). «Трехмерный статистический подход к улучшению качества изображения для многосрезовой спиральной компьютерной томографии» (PDF). Медицинская физика. 34 (11): 4526–4544. Bibcode:2007МедФ..34.4526Т. Дои:10.1118/1.2789499. PMID  18072519.
  10. ^ Hsieh, C.J .; Chang, K. W .; Lin, C.J .; Keerthi, S. S .; Сундарараджан, С. (2008). «Метод двойного координатного спуска для крупномасштабной линейной SVM» (PDF). Материалы 25-й международной конференции по машинному обучению - ICML '08. п. 408. Дои:10.1145/1390156.1390208. ISBN  9781605582054.
  11. ^ Hsieh, C.J .; Диллон, И. С. (2011). Методы быстрого координатного спуска с выбором переменных для факторизации неотрицательной матрицы (PDF). Материалы 17-й международной конференции ACM SIGKDD по открытию знаний и интеллектуальному анализу данных - KDD '11. п. 1064. Дои:10.1145/2020408.2020577. ISBN  9781450308137.
  12. ^ Нестеров Юрий (2012). «Эффективность методов координатного спуска в задачах оптимизации большого масштаба» (PDF). СИАМ Дж. Оптим. 22 (2): 341–362. CiteSeerX  10.1.1.332.3336. Дои:10.1137/100802001.
  • Bezdek, J.C .; Hathaway, R.J .; Howard, R.E .; Wilson, C.A .; Виндхэм, М. П. (1987), "Анализ локальной сходимости версии сгруппированных переменных координатного спуска", Журнал теории оптимизации и приложений, Kluwer Academic / Plenum Publishers, 54 (3), стр. 471–477, Дои:10.1007 / BF00940196
  • Бертсекас, Дмитрий П. (1999). Нелинейное программирование, второе издание Athena Scientific, Белмонт, Массачусетс. ISBN  1-886529-00-0.
  • Канутеску, AA; Данбрак, Р.Л. (2003), «Циклический координатный спуск: робототехнический алгоритм для замыкания белковой петли», Белковая наука, 12 (5), стр. 963–72, Дои:10.1110 / пс.0242703, ЧВК  2323867, PMID  12717019.
  • Ло, Чжицюань; Ценг, П. (1992), "О сходимости метода координатного спуска для выпуклой дифференцируемой минимизации", Журнал теории оптимизации и приложений, Kluwer Academic / Plenum Publishers, 72 (1), стр. 7–35, Дои:10.1007 / BF00939948, HDL:1721.1/3164.
  • Ву, Тонгтонг; Ланге, Кеннет (2008), «Алгоритмы координатного спуска для регрессии со штрафом Лассо», Летопись прикладной статистики, Институт математической статистики, 2 (1), стр. 224–244, arXiv:0803.3876, Дои:10.1214 / 07-AOAS147.
  • Ричтарик, Питер; Такач, Мартин (апрель 2011 г.), «Итерационная сложность рандомизированных методов блочно-координатного спуска для минимизации составной функции», Математическое программирование, Спрингер, 144 (1–2), стр. 1–38, arXiv:1107.2848, Дои:10.1007 / s10107-012-0614-z.
  • Ричтарик, Питер; Такач, Мартин (декабрь 2012 г.), «Методы параллельного координатного спуска для оптимизации больших данных», ArXiv: 1212.0873, arXiv:1212.0873.