Тотиентная функция Эйлера - Википедия - Eulers totient function

Первая тысяча значений φ(п). Точки в верхней строке представляют φ(п) когда п простое число, которое п − 1.^[1]

В теория чисел, Функция Эйлера считает положительные целые числа до заданного целого числа п которые относительно простой к п. Написано греческой буквой фи в качестве φ(п) или же ϕ(п), а также может называться Функция фи Эйлера. Другими словами, это количество целых чисел k В диапазоне 1 ≤ k ≤ п для чего наибольший общий делитель gcd (п, k) равно 1.^[2][3] Целые числа k этой формы иногда называют итоги из п.

Например, всего п = 9 - шесть чисел 1, 2, 4, 5, 7 и 8. Все они взаимно просты с 9, но три других числа в этом диапазоне, 3, 6 и 9, нет, поскольку gcd (9, 3) = gcd (9, 6) = 3 и gcd (9, 9) = 9. Следовательно, φ(9) = 6. Другой пример: φ(1) = 1 поскольку для п = 1 единственное целое число в диапазоне от 1 до п есть 1, и gcd (1, 1) = 1.

Тотальная функция Эйлера - это мультипликативная функция, что означает, что если два числа м и п относительно простые, то φ(мин) = φ(м)φ(п).^[4][5]Эта функция дает порядок из мультипликативная группа целых чисел по модулю п (в группа из единицы из звенеть ℤ/пℤ).^[6] Он также используется для определения Система шифрования RSA.

История, терминология и обозначения

Леонард Эйлер ввел функцию в 1763 году.^[7][8][9] Однако в то время он не выбрал какой-либо конкретный символ для его обозначения. В публикации 1784 года Эйлер дополнительно изучил функцию, выбрав греческую букву π чтобы обозначить это: он написал πD для "множества чисел меньше, чем D, и которые не имеют с ним общего делителя ".^[10] Это определение отличается от текущего определения функции totient в D = 1 но в остальном то же самое. Ныне стандартные обозначения^[8][11] φ(А) происходит от Гаусс трактат 1801 года Disquisitiones Arithmeticae,^[12] хотя Гаусс не использовал скобки вокруг аргумента и написал φA. Таким образом, его часто называют Функция фи Эйлера или просто функция фи.

В 1879 г. Дж. Дж. Сильвестр ввел термин тотент для этой функции^[13][14] поэтому его также называют Функция Эйлера, то Эйлер тотиент, или же Тотентиент Эйлера. Тотент Джордана является обобщением Эйлера.

В cototient из п определяется как п − φ(п). Он подсчитывает количество положительных целых чисел, меньших или равных п у которых есть хотя бы один главный фактор вместе с п.

Вычисление тотентифицирующей функции Эйлера

Есть несколько формул для вычисления φ(п).

Формула произведения Эйлера

Говорится

${ displaystyle varphi (n) = n prod _ {p mid n} left (1 - { frac {1} {p}} right),}$

где произведение находится над отличным простые числа разделение п. (Обозначения см. Арифметическая функция.)

Эквивалентная формулировка для ${ displaystyle n = p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} cdots p_ {r} ^ {k_ {r}}}$, куда ${ displaystyle p_ {1}, p_ {2}, ldots, p_ {r}}$ различные простые числа, делящие п, является:

${ displaystyle varphi (n) = p_ {1} ^ {k_ {1} -1} (p_ {1} {-} 1) , p_ {2} ^ {k_ {2} -1} (p_ { 2} {-} 1) cdots p_ {r} ^ {k_ {r} -1} (p_ {r} {-} 1).}$

Доказательство этих формул зависит от двух важных фактов.

Phi - мультипликативная функция

Это означает, что если gcd (м, п) = 1, тогда φ(м) φ(п) = φ(мин). Схема доказательства: Позволять А, B, C - множества натуральных чисел, которые совмещать до и меньше м, п, минсоответственно, так что |А| = φ(м)и т. д. Тогда есть биекция между А × B и C посредством Китайская теорема об остатках.

Значение фи для аргумента первичной мощности

Если п прост и k ≥ 1, тогда

${ displaystyle varphi left (p ^ {k} right) = p ^ {k} -p ^ {k-1} = p ^ {k-1} (p-1) = p ^ {k} left (1 - { tfrac {1} {p}} right).}$

Доказательство: С п - простое число, единственные возможные значения gcd (п^k, м) находятся 1, п, п², ..., п^k, и единственный способ иметь gcd (п^k, м) > 1 если м кратно п, т.е. м = п, 2п, 3п, ..., п^{k − 1}п = п^k, и здесь п^{k − 1} такие кратные меньше чем п^k. Следовательно, другой п^k − п^{k − 1} числа все взаимно просты с п^k.

Доказательство формулы произведения Эйлера

В основная теорема арифметики заявляет, что если п > 1 есть уникальное выражение ${ displaystyle n = p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} cdots p_ {r} ^ {k_ {r}},}$ куда п₁ < п₂ < ... < п_р находятся простые числа и каждый k_я ≥ 1. (Дело п = 1 соответствует пустому произведению.) Неоднократно используя мультипликативное свойство φ и формула для φ(п^k) дает

${ displaystyle { begin {array} {rcl} varphi (n) & = & varphi (p_ {1} ^ {k_ {1}}) , varphi (p_ {2} ^ {k_ {2}) }) cdots varphi (p_ {r} ^ {k_ {r}}) [. 1em] & = & p_ {1} ^ {k_ {1} -1} (p_ {1} -1) , p_ {2} ^ {k_ {2} -1} (p_ {2} -1) cdots p_ {r} ^ {k_ {r} -1} (p_ {r} -1) [. 1em] & = & p_ {1} ^ {k_ {1}} left (1 - { frac {1} {p_ {1}}} right) p_ {2} ^ {k_ {2}} left (1- { frac {1} {p_ {2}}} right) cdots p_ {r} ^ {k_ {r}} left (1 - { frac {1} {p_ {r}}} right) [. 1em] & = & p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} cdots p_ {r} ^ {k_ {r}} left (1 - { frac {1} {p_ {1}}} right) left (1 - { frac {1} {p_ {2}}} right) cdots left (1 - { frac {1} {p_ {r}}} right) [. 1em] & = & n left (1 - { frac {1} {p_ {1}}} right) left (1 - { frac {1} { p_ {2}}} right) cdots left (1 - { frac {1} {p_ {r}}} right). end {array}}}$

Это дает обе версии формулы произведения Эйлера.

Альтернативное доказательство, которое не требует мультипликативного свойства, вместо этого использует принцип включения-исключения применяется к набору ${ Displaystyle {1,2, ldots, п }}$, исключая наборы целых чисел, делящихся на простые делители.

Пример

${ Displaystyle varphi (20) = varphi (2 ^ {2} 5) = 20 , (1 - { tfrac {1} {2}}) , (1 - { tfrac {1} {5 }}) = 20 cdot { tfrac {1} {2}} cdot { tfrac {4} {5}} = 8.}$

На словах: различные простые делители числа 20 равны 2 и 5; половина из двадцати целых чисел от 1 до 20 делятся на 2, остается десять; пятая часть из них делится на 5, в результате чего восемь чисел взаимно просты с 20; это: 1, 3, 7, 9, 11, 13, 17, 19.

Альтернативная формула использует только целые числа:

${ displaystyle phi (20) = phi (2 ^ {2} 5 ^ {1}) = 2 ^ {2-1} (2 {-} 1) , 5 ^ {1-1} (5 { -} 1) = 2 cdot 1 cdot 1 cdot 4 = 8.}$

преобразование Фурье

Totient - это дискретное преобразование Фурье из gcd, оценивается в 1.^[15] Позволять

${ Displaystyle { mathcal {F}} { mathbf {x} } [m] = sum limits _ {k = 1} ^ {n} x_ {k} cdot e ^ {{- 2 пи i} { frac {mk} {n}}}}$

куда Икс_k = gcd (k,п) за k ∈ {1, …, п}. потом

${ displaystyle varphi (n) = { mathcal {F}} { mathbf {x} } [1] = sum limits _ {k = 1} ^ {n} gcd (k, n) e ^ {- 2 pi i { frac {k} {n}}}.}$

Действительная часть этой формулы:

${ displaystyle varphi (n) = sum limits _ {k = 1} ^ {n} gcd (k, n) cos { tfrac {2 pi k} {n}}.}$

Например, используя ${ displaystyle cos { tfrac { pi} {5}} = { tfrac {{ sqrt {5}} + 1} {4}}}$ и ${ displaystyle cos { tfrac {2 pi} {5}} = { tfrac {{ sqrt {5}} - 1} {4}}}$:

${ Displaystyle { begin {array} {rcl} phi (10) & = & gcd (1,10) cos { tfrac {2 pi} {10}} + gcd (2,10) cos { tfrac {4 pi} {10}} + gcd (3,10) cos { tfrac {6 pi} {10}} + cdots + gcd (10,10) cos { tfrac {20 pi} {10}} & = & 1 cdot ({ tfrac {{ sqrt {5}} + 1} {4}}) + 2 cdot ({ tfrac {{ sqrt { 5}} - 1} {4}}) + 1 cdot (- { tfrac {{ sqrt {5}} - 1} {4}}) + 2 cdot (- { tfrac {{ sqrt { 5}} + 1} {4}}) + 5 cdot (-1) && + 2 cdot (- { tfrac {{ sqrt {5}} + 1} {4}}) + 1 cdot (- { tfrac {{ sqrt {5}} - 1} {4}}) + 2 cdot ({ tfrac {{ sqrt {5}} - 1} {4}}) + 1 cdot ({ tfrac {{ sqrt {5}} + 1} {4}}) + 10 cdot (1) & = & 4. end {array}}}$

В отличие от произведения Эйлера и формулы суммы делителей, эта не требует знания множителей при п. Однако это включает в себя вычисление наибольшего общего делителя п и каждое положительное целое число меньше п, что в любом случае достаточно для факторизации.

Сумма делителя

Собственность, установленная Гауссом,^[16] который

${ displaystyle sum _ {d mid n} varphi (d) = n,}$

где сумма берется по всем положительным делителям d из п, можно доказать несколькими способами. (Видеть Арифметическая функция для условных обозначений.)

Одно из доказательств - отметить, что φ(d) также равно количеству возможных образующих циклическая группа C_d ; в частности, если C_d = ⟨грамм⟩ с грамм^d = 1, тогда грамм^k генератор для каждого k взаимно простой с d. Поскольку каждый элемент C_п генерирует циклический подгруппа, и все подгруппы C_d ⊆ C_п порождаются некоторым элементом C_п, формула следует.^[17] Эквивалентно, формула может быть получена с помощью того же аргумента, примененного к мультипликативной группе пth корни единства и примитивный dкорни единства.

Формулу можно также вывести из элементарной арифметики.^[18] Например, пусть п = 20 и рассмотрим положительные дроби до 1 со знаминателем 20:

${ displaystyle { tfrac {1} {20}}, , { tfrac {2} {20}}, , { tfrac {3} {20}}, , { tfrac {4} {20 }}, , { tfrac {5} {20}}, , { tfrac {6} {20}}, , { tfrac {7} {20}}, , { tfrac {8} {20}}, , { tfrac {9} {20}}, , { tfrac {10} {20}}, , { tfrac {11} {20}}, , { tfrac { 12} {20}}, , { tfrac {13} {20}}, , { tfrac {14} {20}}, , { tfrac {15} {20}}, , { tfrac {16} {20}}, , { tfrac {17} {20}}, , { tfrac {18} {20}}, , { tfrac {19} {20}}, , { tfrac {20} {20}}.}$

Поместите их в самые низкие сроки:

${ displaystyle { tfrac {1} {20}}, , { tfrac {1} {10}}, , { tfrac {3} {20}}, , { tfrac {1} {5 }}, , { tfrac {1} {4}}, , { tfrac {3} {10}}, , { tfrac {7} {20}}, , { tfrac {2} {5}}, , { tfrac {9} {20}}, , { tfrac {1} {2}}, , { tfrac {11} {20}}, , { tfrac { 3} {5}}, , { tfrac {13} {20}}, , { tfrac {7} {10}}, , { tfrac {3} {4}}, , { tfrac {4} {5}}, , { tfrac {17} {20}}, , { tfrac {9} {10}}, , { tfrac {19} {20}}, , { tfrac {1} {1}}}$

Эти двадцать фракций все положительные k/d ≤ 1, знаменателями которых являются делители d = 1, 2, 4, 5, 10, 20. Дроби со знаменателем 20 - это дроби, числители которых взаимно просты с 20, а именно 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20; по определению это φ(20) фракции. Точно так же есть φ(10) дроби со знаминателем 10, и φ(5) дроби со знаминателем 5 и т. д. Таким образом, набор из двадцати дробей разбивается на подмножества размера φ(d) для каждого d деление 20. Аналогичный аргумент применим к любому п.

Инверсия Мёбиуса примененная к формуле суммы делителей дает

${ displaystyle varphi (n) = sum _ {d mid n} mu left (d right) cdot { frac {n} {d}} = n sum _ {d mid n} { frac { mu (d)} {d}},}$

куда μ это Функция Мёбиуса, то мультипликативная функция определяется ${ displaystyle mu (p) = - 1}$ и ${ Displaystyle му (п ^ {к}) = 0}$ для каждого прайма п и k ≥ 1. Эта формула также может быть получена из формулы произведения путем умножения ${ displaystyle textstyle prod _ {p mid n} (1 - { frac {1} {p}})}$ получить ${ displaystyle textstyle sum _ {d mid n} { frac { mu (d)} {d}}.}$

Пример:

${ Displaystyle { begin {выровнено} phi (20) & = mu (1) cdot 20+ mu (2) cdot 10+ mu (4) cdot 5+ mu (5) cdot 4+ mu (10) cdot 2+ mu (20) cdot 1 [. 5em] & = 1 cdot 20-1 cdot 10 + 0 cdot 5-1 cdot 4 + 1 cdot 2 + 0 cdot 1 = 8. End {align}}}$

Некоторые ценности

Первые 100 значений (последовательность A000010 в OEIS ) показаны в таблице и на графике ниже:

График первых 100 значений

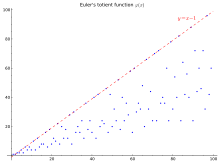
φ(п) за 1 ≤ п ≤ 100

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

На графике справа в верхней строке у = п − 1 является верхняя граница действительно для всех п кроме одного, и достигается тогда и только тогда, когда п простое число. Простая нижняя оценка ${ Displaystyle varphi (п) geq { sqrt {п / 2}}}$, который довольно рыхлый: на самом деле Нижний предел графика пропорциональна п/журнал журнал п.^[19]

Теорема Эйлера

Это гласит, что если а и п находятся относительно простой тогда

${ displaystyle a ^ { varphi (n)} Equiv 1 mod n.}$

Частный случай, когда п простой известен как Маленькая теорема Ферма.

Это следует из Теорема Лагранжа и тот факт, что φ(п) это порядок из мультипликативная группа целых чисел по модулю п.

В Криптосистема RSA основана на этой теореме: из нее следует, что обратный функции а ↦ а^е мод п, куда е - показатель степени шифрования (публичный), - функция б ↦ б^d мод п, куда d, (частный) показатель расшифровки, является мультипликативный обратный из е по модулю φ(п). Сложность вычислений φ(п) не зная факторизации п таким образом, сложность вычисления d: это известно как Проблема RSA что может быть решено факторингом п. Владелец закрытого ключа знает факторизацию, поскольку закрытый ключ RSA создается путем выбора п как произведение двух (случайно выбранных) больших простых чисел п и q. Только п публично раскрывается, и с учетом сложность разложения больших чисел у нас есть гарантия, что никто другой не знает факторизацию.

Другие формулы

• ${ displaystyle a mid b подразумевает varphi (a) mid varphi (b)}$
• ${ displaystyle n mid varphi (a ^ {n} -1) quad { text {for}} a, n> 1}$
• ${ displaystyle varphi (mn) = varphi (m) varphi (n) cdot { frac {d} { varphi (d)}} quad { text {where}} d = operatorname {gcd } (m, n)}$

Обратите внимание на особые случаи

• ${ displaystyle varphi (2m) = { begin {case} 2 varphi (m) & { text {if}} m { text {четно}} varphi (m) & { text { if}} m { text {нечетное}} end {case}}}$
• ${ displaystyle varphi left (п ^ {m} right) = n ^ {m-1} varphi (n)}$

• ${ displaystyle varphi ( operatorname {lcm} (m, n)) cdot varphi ( operatorname {gcd} (m, n)) = varphi (m) cdot varphi (n)}$

Сравните это с формулой

• ${ displaystyle operatorname {lcm} (m, n) cdot operatorname {gcd} (m, n) = m cdot n}$

(Видеть наименьший общий множитель.)

• φ(п) даже для п ≥ 3. Более того, если п имеет р различные нечетные простые множители, 2^р | φ(п)
• Для любого а > 1 и п > 6 такой, что 4 ∤ п существует л ≥ 2п такой, что л | φ(а^п − 1).
• ${ displaystyle { frac { varphi (n)} {n}} = { frac { varphi ( operatorname {rad} (n))} { operatorname {rad} (n)}}}$

куда рад (п) это радикал п (произведение всех различных простых чисел, делящих п ).

• ${ displaystyle sum _ {d mid n} { frac { mu ^ {2} (d)} { varphi (d)}} = { frac {n} { varphi (n)}}}$ ^[20]
• ${ Displaystyle сумма _ {1 Leq к Leq п на вершине (к, п) = 1} ! ! к = { tfrac {1} {2}} п varphi (п) квад { текст {for}} n> 1}$
• ${ displaystyle sum _ {k = 1} ^ {n} varphi (k) = { tfrac {1} {2}} left (1+ sum _ {k = 1} ^ {n} mu (k) left lfloor { frac {n} {k}} right rfloor ^ {2} right) = { frac {3} { pi ^ {2}}} n ^ {2} + O left (n ( log n) ^ { frac {2} {3}} ( log log n) ^ { frac {4} {3}} right)}$ (^[21] цитируется в^[22])

• ${ displaystyle sum _ {k = 1} ^ {n} { frac { varphi (k)} {k}} = sum _ {k = 1} ^ {n} { frac { mu (k )} {k}} left lfloor { frac {n} {k}} right rfloor = { frac {6} { pi ^ {2}}} n + O left (( log n ) ^ { frac {2} {3}} ( log log n) ^ { frac {4} {3}} right)}$ ^[21]
• ${ displaystyle sum _ {k = 1} ^ {n} { frac {k} { varphi (k)}} = { frac {315 , zeta (3)} {2 pi ^ {4 }}} n - { frac { log n} {2}} + O left (( log n) ^ { frac {2} {3}} right)}$ ^[23]
• ${ displaystyle sum _ {k = 1} ^ {n} { frac {1} { varphi (k)}} = { frac {315 , zeta (3)} {2 pi ^ {4 }}} left ( log n + gamma - sum _ {p { text {prime}}} { frac { log p} {p ^ {2} -p + 1}} right) + O left ({ frac {( log n) ^ { frac {2} {3}}} {n}} right)}$ ^[23]

(куда γ это Константа Эйлера – Маскерони ).

• ${ displaystyle sum _ { stackrel {1 leq k leq n} { operatorname {gcd} (k, m) = 1}} ! ! ! ! 1 = n { frac { varphi (m)} {m}} + O left (2 ^ { omega (m)} right)}$

куда м > 1 положительное целое число и ω(м) количество различных простых делителей м.^[24]

Личность Менона

В 1965 г. П. Кесава Менон доказал

${ Displaystyle сумма _ { stackrel {1 leq k leq n} { gcd (k, n) = 1}} ! ! ! ! gcd (k-1, n) = varphi (n) d (n),}$

куда d(п) = σ₀(п) это количество делителей п.

Формулы с золотым сечением

Шнайдер^[25] нашли пару тождеств, соединяющих общую функцию, Золотое сечение и Функция Мёбиуса μ(п). В этой секции φ(п) - общая функция, а ϕ = 1 + √5/2 = 1.618… это золотое сечение.

Они есть:

${ displaystyle phi = - sum _ {k = 1} ^ { infty} { frac { varphi (k)} {k}} log left (1 - { frac {1} { phi ^ {k}}} right)}$

и

${ displaystyle { frac {1} { phi}} = - sum _ {k = 1} ^ { infty} { frac { mu (k)} {k}} log left (1- { frac {1} { phi ^ {k}}} right).}$

Их вычитание дает

${ displaystyle sum _ {k = 1} ^ { infty} { frac { mu (k) - varphi (k)} {k}} log left (1 - { frac {1} { phi ^ {k}}} right) = 1.}$

Применение экспоненциальной функции к обеим частям предыдущего тождества дает формулу бесконечного произведения для е:

${ displaystyle e = prod _ {k = 1} ^ { infty} left (1 - { frac {1} { phi ^ {k}}} right) ! ! ^ { frac { mu (k) - varphi (k)} {k}}.}$

Доказательство основано на двух формулах

${ displaystyle { begin {align} sum _ {k = 1} ^ { infty} { frac { varphi (k)} {k}} left (- log left (1-x ^ { k} right) right) & = { frac {x} {1-x}} { text {and}} ; sum _ {k = 1} ^ { infty} { frac { mu (k)} {k}} left (- log left (1-x ^ {k} right) right) & = x, qquad quad { text {for}} 0$

Производящие функции

В Серия Дирихле за φ(п) можно записать в терминах Дзета-функция Римана в качестве:^[26]

${ displaystyle sum _ {n = 1} ^ { infty} { frac { varphi (n)} {n ^ {s}}} = { frac { zeta (s-1)} { zeta (s)}}.}$

В Серия Ламберта производящая функция^[27]

${ displaystyle sum _ {n = 1} ^ { infty} { frac { varphi (n) q ^ {n}} {1-q ^ {n}}} = { frac {q} {( 1-q) ^ {2}}}}$

который сходится для |q| < 1.

Оба эти утверждения доказываются манипуляциями с элементарными рядами и формулами для φ(п).

Скорость роста

По словам Харди и Райта, порядок φ(п) "всегда" почти п’.”^[28]

Первый^[29]

${ displaystyle lim sup { frac { varphi (n)} {n}} = 1,}$

но, как п уходит в бесконечность,^[30] для всех δ > 0

${ displaystyle { frac { varphi (n)} {n ^ {1- delta}}} rightarrow infty.}$

Эти две формулы можно доказать, используя немногим больше, чем формулы для φ(п) и функция суммы делителей σ(п).

На самом деле, при доказательстве второй формулы неравенство

${ displaystyle { frac {6} { pi ^ {2}}} <{ frac { varphi (n) sigma (n)} {n ^ {2}}} <1,}$

верно для п > 1, доказано.

У нас также есть^[19]

${ displaystyle lim inf { frac { varphi (n)} {n}} log log n = e ^ {- gamma}.}$

Здесь γ является Постоянная Эйлера, γ = 0.577215665..., так е^γ = 1.7810724... и е^−γ = 0.56145948....

Доказательство этого не совсем требует теорема о простых числах.^[31][32] С журнал журнал п уходит в бесконечность, эта формула показывает, что

${ displaystyle lim inf { frac { varphi (n)} {n}} = 0.}$

На самом деле, правда больше.^[33][34][35]

${ displaystyle varphi (n)> { frac {n} {e ^ { gamma} ; log log n + { frac {3} { log log n}}}} quad { text {for}} n> 2}$

и

${ displaystyle varphi (n) <{ frac {n} {e ^ { gamma} log log n}} quad { text {для бесконечного числа}} n.}$

Второе неравенство было показано Жан-Луи Николя. Рибенбойм говорит: «Метод доказательства интересен тем, что неравенство сначала показано в предположении, что Гипотеза Римана верно, во-вторых, при обратном предположении ".^[35]

Для среднего заказа имеем^[21][36]

${ displaystyle varphi (1) + varphi (2) + cdots + varphi (n) = { frac {3n ^ {2}} { pi ^ {2}}} + O left (n ( log n) ^ { frac {2} {3}} ( log log n) ^ { frac {4} {3}} right) quad { text {as}} n rightarrow infty ,}$

из-за Арнольд Вальфис, в его доказательстве используются оценки экспоненциальных сумм Виноградов И. М. и Коробов Н. М. (в настоящее время это наиболее известная оценка такого типа). В "Большой О" обозначает величину, которая ограничена постоянным умножением на функцию п внутри скобок (что мало по сравнению с п²).

Этот результат можно использовать для доказательства^[37] что вероятность того, что два случайно выбранных числа будут относительно простыми, равна 6/π².

Соотношение последовательных значений

В 1950 году Сомаяджулу доказал, что^[38][39]

${ displaystyle { begin {align} lim inf { frac { varphi (n + 1)} { varphi (n)}} & = 0 quad { text {and}} [5px] lim sup { frac { varphi (n + 1)} { varphi (n)}} & = infty. end {align}}}$

В 1954 г. Шинцель и Серпинский укрепили это, доказав^[38][39] что набор

${ displaystyle left {{ frac { varphi (n + 1)} { varphi (n)}}, ; ; n = 1,2, ldots right }}$

является плотный в положительных вещественных числах. Они также доказали^[38] что набор

${ displaystyle left {{ frac { varphi (n)} {n}}, ; ; n = 1,2, ldots right }}$

плотно в интервале (0,1).

Totient числа

А номер телефона является значением тотентифицирующей функции Эйлера: то есть м для которых есть хотя бы один п для которого φ(п) = м. В валентность или же множественность общего числа м - количество решений этого уравнения.^[40] А неуловимый натуральное число, не являющееся общим числом. Каждое нечетное целое число, превышающее 1, тривиально неточность. Также существует бесконечно много даже не-сущностей,^[41] и действительно, каждое положительное целое число имеет кратное, которое не является четным.^[42]

Количество общих чисел до заданного предела Икс является

${ displaystyle { frac {x} { log x}} e ^ { big (} C + o (1) { big)} ( log log log x) ^ {2}}}$

для постоянного C = 0.8178146....^[43]

Если считать по множественности, количество общих чисел до заданного предела Икс является

${ displaystyle { Big vert} {n: phi (n) leq x } { Big vert} = { frac { zeta (2) zeta (3)} { zeta (6 )}} cdot x + R (x)}$

где термин ошибки р в порядке самое большее Икс/(бревно Икс)^k для любого положительного k.^[44]

Известно, что кратность м превышает м^δ бесконечно часто для любого δ < 0.55655.^[45][46]

Теорема Форда

Форд (1999) доказал, что для каждого целого k ≥ 2 есть общий номер м множественности k: то есть, для которого уравнение φ(п) = м точно k решения; этот результат ранее был предположен Вацлав Серпинский,^[47] и он был получен в результате Гипотеза Шинцеля H.^[43] В самом деле, каждая встречающаяся множественность происходит бесконечно часто.^[43][46]

Однако нет числа м известен во множестве k = 1. Гипотеза кармайкла о функции тотализатора это утверждение, что нет такого м.^[48]

Идеальные общие числа

Приложения

Циклотомия

В последнем разделе Disquisitiones^[49][50] Гаусс доказывает^[51] что регулярный п-угольник может быть построен с помощью линейки и циркуля, если φ(п) является степенью 2. Если п является степенью нечетного простого числа, формула для totient говорит, что его totient может быть степенью двойки, только если п это первая сила и п − 1 является степенью 2. Простые числа, которые на единицу больше степени двойки, называются Простые числа Ферма, а известно только пять: 3, 5, 17, 257 и 65537. Ферма и Гаусс знали об этом. Никто не смог доказать, есть ли еще.

Таким образом, регулярный п-gon имеет конструкцию линейки и циркуля, если п является произведением различных простых чисел Ферма и любой степени двойки. Первые несколько таких п находятся^[52]

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, ... (последовательность A003401 в OEIS ).

Криптосистема RSA

Настройка системы RSA включает выбор больших простых чисел п и q, вычисление п = pq и k = φ(п), и найдя два числа е и d такой, что ред ≡ 1 (мод k). Цифры п и е («ключ шифрования») публикуются, и d («ключ дешифрования») хранится в секрете.

Сообщение, представленное целым числом м, куда 0 < м < п, зашифровано вычислением S = м^е (мод п).

Он расшифровывается с помощью вычислений т = S^d (мод п). Теорема Эйлера может быть использована, чтобы показать, что если 0 < т < п, тогда т = м.

Безопасность системы RSA будет поставлена ​​под угрозу, если номер п могут быть учтены или если φ(п) можно вычислить без факторинга п.

Нерешенные проблемы

Гипотеза Лемера

Если п простое, то φ(п) = п − 1. В 1932 г. Д. Х. Лемер спросил, есть ли составные числа п такой, что φ(п) разделяет п − 1. Никто не известен.^[53]

В 1933 году он доказал, что если такие п существует, он должен быть нечетным, не содержать квадратов и делиться не менее чем на семь простых чисел (т.е. ω(п) ≥ 7). В 1980 году Коэн и Хагис доказали, что п > 10²⁰ и это ω(п) ≥ 14.^[54] Далее Хагис показал, что если 3 делит п тогда п > 10^1937042 и ω(п) ≥ 298848.^[55][56]

Гипотеза Кармайкла

Это говорит о том, что нет числа п с тем свойством, что для всех остальных номеров м, м ≠ п, φ(м) ≠ φ(п). Видеть Теорема Форда над.

Как указано в основной статье, если существует единственный контрпример к этой гипотезе, должно быть бесконечно много контрпримеров, а самый маленький из них содержит не менее десяти миллиардов цифр в базе 10.^[40]

Смотрите также

• Функция Кармайкла
• Гипотеза Даффина – Шеффера
• Обобщения малой теоремы Ферма
• Сильно составное число
• Мультипликативная группа целых чисел по модулю п
• Рамануджанская сумма
• Тотент-сумматорная функция

Примечания

Рекомендации

внешняя ссылка

• "Totient функция", Энциклопедия математики, EMS Press, 2001 [1994]
• Фи-функция Эйлера и китайская теорема об остатках - доказательство того, что φ(п) мультипликативный
• Калькулятор функции Эйлера в JavaScript - до 20 цифр
• Динева, Росица, Функции Эйлера, Мёбиуса и делителя.
• Плитадж, Лумис, Полхилл Подведение итогов по функции Эйлера-Фи