Синтаксис и символы APL - APL syntax and symbols
Эта статья может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: В статье нестандартная верстка и форматирование. (Октябрь 2015) (Узнайте, как и когда удалить этот шаблон сообщения) |
Язык программирования APL отличается тем, что символический скорее, чем лексический: его примитивы обозначаются символыа не слова. Эти символы изначально задумывались как математическая запись для описания алгоритмов.[1] Программисты APL часто назначают неформальные имена при обсуждении функций и операторов (например, продукт для × /), но основные функции и операторы, предоставляемые языком, обозначаются нетекстовыми символами.
Монадические и диадические функции
Большинство символов обозначают функции или же операторы. А монадический функция принимает в качестве аргумента результат оценки всего, что находится справа. (Обычно модерируется скобками.) A диадический функция имеет еще один аргумент, первый элемент данных слева. Многие символы обозначают как монадические, так и диадические функции, интерпретируемые в зависимости от использования. Например, ⌊3,2 дает 3, наибольшее целое число, не превышающее аргумент, а 3⌊2 дает 2, меньшее из двух аргументов.
Функции и операторы
APL использует термин оператор в Хевисайд Смысл модератора функции в отличие от использования какого-либо другого языка программирования того же термина как что-то, что работает с данными, исх. реляционный оператор и операторы в целом. В других языках программирования этот термин также иногда используется как синоним функция, однако оба термина используются в APL более точно.[2][3][4][5][6] Ранние определения символов APL были очень конкретными в отношении того, как символы классифицируются.[7] Например, оператор уменьшать обозначается косой чертой и уменьшает массив вдоль одной оси, вставляя его функцию операнд. Пример уменьшать:
×/2 3 424 | << Эквивалент результаты в APL >> << Уменьшать оператор / используется слева | 2×3×424 |
В приведенном выше случае уменьшать или же слэш оператор модерирует в умножать функция. Выражение ×/2 3 4 вычисляет скалярный результат (только 1 элемент) через сокращение массив умножением. Приведенный выше случай упрощен: представьте себе умножение (сложение, вычитание или деление) большего, чем просто нескольких чисел вместе. (Из вектора, ×/ возвращает произведение всех своих элементов.)
1 0 1\45 6745 0 67 | << Противоположный результаты в APL >> << Развернуть диадическая функция \ используется слева Тиражировать диадическая функция / используется справа >> | 1 0 1/45 0 6745 67 |
Вышесказанное диадические функции примеры [левый и правый примеры] (с использованием того же / символ, пример справа) демонстрируют, как логический значения (0 и 1) могут использоваться в качестве левых аргументов для расширять и / реплицировать функции для получения прямо противоположных результатов. С левой стороны 2-элементный вектор {45 67} есть расширенный где логические 0 приводят к 3-элементный vector {45 0 67} - обратите внимание, как APL вставил 0 в вектор. И наоборот, с правой стороны происходит прямо противоположное - где 3-элементный вектор становится 2-элементным; логические 0 Удалить предметы, использующие диадические / слэш функция. Символы APL также действуют на списки (вектор) элементов, использующих типы данных, отличные от числовых, например, двухэлементный вектор символьных строк {"Яблоки" "Апельсины"} может быть заменен числовым вектором {45 67} выше.
Правила синтаксиса
В APL нет иерархия приоритета для функций или операторов. APL не следует обычным приоритет оператора других языков программирования; Например, × не связывает свои операнды более "жестко", чем +. Вместо приоритета операторов APL определяет понятие объем.
В объем из функция определяет его аргументы. Функции имеют длинный правый прицел: то есть они принимают за правильные аргументы все, что им положено. Диадическая функция имеет короткий левый прицел: он принимает в качестве левого аргумента первую часть данных слева от него. Например, (крайний левый столбец ниже актуален программный код из APL пользовательская сессия, отступ = фактический пользовательский ввод, без отступа = результат, возвращенный Интерпретатор APL ):
1 ÷ 2 ⌊ 3 × 4 - 5¯0.3333333333 1 ÷ 2 ⌊ 3 × ¯1¯0.3333333333 1 ÷ 2 ⌊ ¯3¯0.3333333333 1 ÷ ¯3¯0.3333333333
| << Первое примечание: скобок и Шаг 2) 3 раза -1 = -3. |
Оператор может иметь функцию или данные операнды и вычислить диадическую или монадическую функцию. Операторы давно покинули сферу деятельности. Оператор принимает в качестве левого операнда самую длинную функцию слева от него. Например:
∘.=/⍳¨3 3 1 0 0 0 1 0 0 0 1
| APL атомный или частичный субанализ (полное объяснение): В диэрезис ¨ или мини-двойная точка означает повторение или же по каждому или же выполнять каждую отдельно так йота повторяется (на человеческом языке, то есть в обратном порядке, интерпретатор APL читает 3 3 на каждую йоту использования), кратко: йота за каждые 3. |
Левый операнд для сверх каждого оператор ¨ это индекс ⍳ функция. В производная функция ⍳¨ используется монадически и принимает в качестве правого операнда вектор 3 3. Левый прицел каждый прекращается уменьшать оператор, обозначаемый форвардом слэш. Его левый операнд - это выражение функции слева от него: внешний продукт из равно функция. Результат ∘. = / Является монадической функцией. При обычной длинной правой области видимости функции она принимает в качестве своего правого аргумента результат ⍳¨3 3. Таким образом,
(⍳3)(⍳3)1 2 3 1 2 3 (⍳3)∘.=⍳31 0 00 1 00 0 1 ⍳¨3 31 2 3 1 2 3 ∘.=/⍳¨3 3 1 0 0 0 1 0 0 0 1
|
Матрица единиц и нулей, полученная аналогично ∘.=/⍳¨3 3 и (⍳3)∘.=⍳3 называется единичная матрица. Матрицы идентичности полезны при решении детерминанты матрицы, группы линейные уравнения и множественная регрессия. |
я ← ∘.=⍨∘⍳ я 3 1 0 0 0 1 0 0 0 1
| Некоторые интерпретаторы APL поддерживают сочинять оператор ∘ и ездить оператор ⍨. Бывший ∘ клеи функционирует вместе, так что foo∘bar, например, может быть гипотетическая функция, которая применяет определенную функцию фу к результату определенной функции бар; foo и bar могут представлять любой существующая функция. В случаях, когда диадическая функция модерируется ездить а затем используется монадически, его правый аргумент также принимается как его левый аргумент. Таким образом, полученный или же составлен функция (названная я слева) используется в пользовательском сеансе APL для возврата 9-элемент единичная матрица, использующая свое право аргумент, параметр или операнд = 3. |
Буквы←"ABCDE" БуквыABCDE ⍴Буквы5 Найди это←"КАБИНЫ" Найди этоКАБИНЫ ⍴Найди это4 Буквы ⍳ Найди это3 1 2 6
| Пример использования APL для индекс ⍳ или же найти (или не найти) элементы в векторе символов: Во-первых, переменная Буквы задается вектор из 5 элементов, в данном случае - букв алфавита. В форма ⍴ или длина вектора символов Буквы 5. Переменная Найди это назначено, что ищи в Буквы и его длина составляет 4 символа. 1 2 3 4 5 << векторные позиции или номера индекса в Буквы Слева диадическая функция йота поиски через его левый аргумент (Letters) для строки поиска (правый аргумент iota, FindIt). Йота находит букву «C» в позиции 3 в буквах, она находит «A» в позиции 1 и «B» в позиции 2. Йота делает не найти буквы" в любом месте переменной Letters, поэтому он возвращает число 6, которое 1 больше длины писем. Йота найденные письма «КАБИНА» (3 1 2). Йота правильно сделал не найти «S» (6). |
Монадические функции
| Имя (а) | Обозначение | Смысл | Кодовая точка Unicode |
|---|---|---|---|
| Рулон | ? B | Одно целое число, выбранное случайным образом из первого B целые числа | U + 003F ? |
| Потолок | ⌈B | Наименьшее целое число больше или равно B | U + 2308 ⌈ |
| Этаж | ⌊B | Наибольшее целое число меньше или равно B | U + 230A ⌊ |
| Форма, Ро | ⍴B | Количество компонентов в каждом измерении B | U + 2374 ⍴ |
| Нет, Тильда | ∼B | Логично: ∼1 равно 0, ∼0 равно 1 | U + 223C ∼ |
| Абсолютная величина | ∣B | Величина B | U + 2223 ∣ |
| Генератор индекса, Йота | ⍳B | Вектор первого B целые числа | U + 2373 ⍳ |
| Экспоненциальный | ⋆B | е в B мощность | U + 22C6 ⋆ |
| Отрицание | −B | Меняет знак B | U + 2212 − |
| Конъюгировать | + B | Комплексное сопряжение B (действительные числа возвращаются без изменений) | U + 002B + |
| Signum | × B | ¯1, если B<0; 0 если B= 0; 1 если B>0 | U + 00D7 × |
| Взаимный | ÷ B | 1 делится на B | U + 00F7 ÷ |
| Равель, Катенат, Ламинат | , B | Перекраивает B в вектор | U + 002C , |
| Матрица обратная, Монадическое разделение на квадраты | ⌹B | Обратная матрица B | U + 2339 ⌹ |
| число Пи раз | ○ B | Умножить на π | U + 25CB ○ |
| Логарифм | ⍟B | Натуральный логарифм B | U + 235F ⍟ |
| Разворот | ⌽B | Обратные элементы B по последней оси | U + 233D ⌽ |
| Разворот | ⊖B | Обратные элементы B по первой оси | U + 2296 ⊖ |
| Оценка выше | ⍋B | Индексы B который устроит B в порядке возрастания | U + 234B ⍋ |
| Вниз | ⍒B | Индексы B который устроит B в порядке убывания | U + 2352 ⍒ |
| Выполнять | ⍎B | Выполнить APL выражение | U + 234E ⍎ |
| Монадический формат | ⍕B | Символьное представление B | U + 2355 ⍕ |
| Монадический транспонировать | ⍉B | Поменять оси B | U + 2349 ⍉ |
| Факториал | ! B | Произведение целых чисел от 1 до B | U + 0021 ! |
Диадические функции
| Имя (а) | Обозначение | Смысл | Unicode кодовая точка |
|---|---|---|---|
| Добавлять | А + В | Сумма А и B | U + 002B + |
| Вычесть | А-Б | А минус B | U + 2212 − |
| Умножить | A × B | А умножается на B | U + 00D7 × |
| Разделять | A ÷ B | А деленное на B | U + 00F7 ÷ |
| Возведение в степень | A⋆B | А поднял до B мощность | U + 22C6 ⋆ |
| Круг | А ○ Б | Тригонометрические функции B выбран АА= 1: грех (B) А= 5: sinh (B)А= 2: cos (B) А= 6: ch (B)А= 3: загар (B) А= 7: tanh (B) Отрицательные числа производят обратные соответствующие функции | U + 25CB ○ |
| Иметь дело | А? Б | А различные целые числа, выбранные случайным образом из первого B целые числа | U + 003F ? |
| Членство, Эпсилон | A∈B | 1 для элементов А присутствует в B; 0 где нет. | U + 2208 ∈ |
| Максимум, Потолок | A⌈B | Большее значение А или же B | U + 2308 ⌈ |
| Минимум, Этаж | A⌊B | Меньшее значение А или же B | U + 230A ⌊ |
| Изменить форму, диадический Ро | A⍴B | Массив формы А с данными B | U + 2374 ⍴ |
| Брать | А ↑ Б | Выберите первый (или последний) А элементы B согласно ×А | U + 2191 ↑ |
| Уронить | А ↓ Б | Удалите первый (или последний) А элементы B согласно ×А | U + 2193 ↓ |
| Декодировать | A⊥B | Значение полинома, коэффициенты которого равны B в А | U + 22A5 ⊥ |
| Кодировать | A⊤B | Основание-А представление ценности B | U + 22A4 ⊤ |
| Остаток | A∣B | B по модулю А | U + 2223 ∣ |
| Цепочка | А, Б | Элементы B добавлен к элементам А | U + 002C , |
| Расширение, диадическая обратная косая черта | А Б | Вставьте нули (или пробелы) в B соответствующие нули в А | U + 005C \ |
| Сжатие, Диадический слэш | А / Б | Выбрать элементы в B соответствующие тем в А | U + 002F / |
| Индекс, диадический Йота | A⍳B | Расположение (индекс) B в А; 1+⍴А если не найден | U + 2373 ⍳ |
| Разделение матрицы, разделение на два квадрата | A⌹B | Решение для система линейных уравнений, множественная регрессия Ах = B | U + 2339 ⌹ |
| Вращение | A⌽B | Элементы B вращаются А позиции | U + 233D ⌽ |
| Вращение | A⊖B | Элементы B вращаются А позиции по первой оси | U + 2296 ⊖ |
| Логарифм | A⍟B | Логарифм B основать А | U + 235F ⍟ |
| Диадический формат | A⍕B | Формат B в матрицу символов согласно А | U + 2355 ⍕ |
| Общее транспонирование | A⍉B | Оси B заказаны А | U + 2349 ⍉ |
| Комбинации | А! Б | Количество комбинаций B взятый А вовремя | U + 0021 ! |
| Диэрезис, Дерезис, Двойная точка | A¨B | Над каждым, или выполнять каждое отдельно; B = на них; А = операция для выполнения или использования (например, йота) | U + 00A8 ¨ |
| Меньше, чем | А <В | Сравнение: 1, если правда, 0, если ложь | U + 003C < |
| Меньше или равно | A≤B | Сравнение: 1, если правда, 0, если ложь | U + 2264 ≤ |
| Равный | А = В | Сравнение: 1, если правда, 0, если ложь | U + 003D = |
| Больше или равно | A≥B | Сравнение: 1, если правда, 0, если ложь | U + 2265 ≥ |
| Лучше чем | А> В | Сравнение: 1, если правда, 0, если ложь | U + 003E > |
| Не равный | А ≠ Б | Сравнение: 1, если правда, 0, если ложь | U + 2260 ≠ |
| Или же | A∨B | Логическая логика: 0 (Ложь) если обе А и B = 0, 1 иначе. Alt: 1 (Верно) если А или же B = 1 (Истинный) | U + 2228 ∨ |
| И | A∧B | Логическая логика: 1 (Верно) если обе А и B = 1, 0 (Ложь) в противном случае | U + 2227 ∧ |
| Ни | A⍱B | Логическая логика: 1, если оба А и B равны 0, иначе 0. Alt: ~ ∨ = not Или | U + 2371 ⍱ |
| Nand | A⍲B | Логическая логика: 0, если оба А и B равны 1, иначе 1. Alt: ~ ∧ = not And | U + 2372 ⍲ |
| Оставили | A⊣B | А | U + 22A3 ⊣ |
| Правильно | A⊢B | B | U + 22A2 ⊢ |
Операторы и индикатор оси
| Имя (а) | Символ | Пример | Значение (примера) | Последовательность кодовой точки Unicode |
|---|---|---|---|---|
| Уменьшить (последняя ось), косая черта | / | + / B | Сумма по B | U + 002F / |
| Уменьшить (первая ось) | ⌿ | + ⌿B | Суммировать B | U + 233F ⌿ |
| Сканирование (последняя ось), обратная косая черта | \ | + B | Текущая сумма по B | U + 005C \ |
| Сканирование (первая ось) | ⍀ | + ⍀B | Подводя итоги B | U + 2340 ⍀ |
| Внутренний продукт | . | А +. × В | Матричный продукт из А и B | U + 002E . |
| Внешний продукт | ∘. | A∘. × B | Внешний продукт из А и B | U + 2218 ∘ , U + 002E . |
Примечания: Операторы сокращения и сканирования ожидают, что слева от них будет двоичная функция, образуя монадическую составную функцию, применяемую к вектору справа.
Оператор продукта "." ожидает диадическую функцию как слева, так и справа, образуя диадическую составную функцию, применяемую к векторам слева и справа. Если функция слева от точки - «∘» (обозначающая ноль), то составная функция является внешним продуктом, в противном случае - внутренним продуктом. Внутренний продукт, предназначенный для обычного умножения матриц, использует функции + и ×, замена их другими двоичными функциями может привести к полезным альтернативным операциям.
За некоторыми функциями может следовать индикатор оси в (квадратных) скобках, т.е. он появляется между функцией и массивом, и его не следует путать с индексами массива, написанными после массива. Например, учитывая функцию ⌽ (разворота) и двумерный массив, функция по умолчанию работает вдоль последней оси, но это можно изменить с помощью индикатора оси:
А←4 3⍴⍳12 А 1 2 3 4 5 6 7 8 910 11 12 ⌽А 3 2 1 6 5 4 9 8 712 11 10 ⌽[1]А10 11 12 7 8 9 4 5 6 1 2 3 ⊖⌽А12 11 10 9 8 7 6 5 4 3 2 1 ⍉А1 4 7 102 5 8 113 6 9 12
|
А теперь отражается или переворачивается по вертикальной оси как символ ⌽ визуально указывает. А теперь отражается с помощью [1] индикатор оси или же модификатор первого измерения. В результате переменная A была отражена по горизонтальной оси, а не по вертикали. А теперь отражается как вертикально ⊖ и по горизонтали ⌽. А является ⍉ транспонированный в матрицу размером 3 строки на 4 столбца, так что строки-столбцы меняются местами, как символ ⍉ визуально изображает. Сравните результат здесь с исходной матрицей, хранящейся в самой верхней матрице A. Эти типы преобразований данных полезны в Временные ряды анализ и пространственные координаты, всего два примера, больше существует. |
Как частный случай, если диадическая родственный "," за функцией следует индикатор оси (или же модификатор оси к символу / функции), его можно использовать для ламинирования (вставки) двух массивов в зависимости от того, является ли индикатор оси меньше или больше, чем происхождение индекса[8] (начало индекса = 1 на иллюстрации ниже):
B←1 2 3 4 C←5 6 7 8 B,C1 2 3 4 5 6 7 8 B,[0.5]C1 2 3 45 6 7 8 B,[1.5]C1 52 63 74 8
| Слева переменной 'B' сначала присваивается вектор из 4 последовательных целых чисел (например, ⍳4). |
Вложенные массивы
Массивы структуры, элементы которых сгруппированы линейно как векторов или в виде таблицы как матрицы - и более высокие измерения (3D или куб, 4D или куб с течением времени, так далее.). Массивы, содержащие как символы, так и числа, называются смешанные массивы.[9] Структуры массивов, содержащие элементы, которые также являются массивами, называются вложенные массивы.[10]
| Пользовательская сессия с интерпретатором APL | Объяснение |
|---|---|
Икс←4 5⍴⍳20 Икс 1 2 3 4 5 6 7 8 9 1011 12 13 14 1516 17 18 19 20 Икс[2;2]7 ⎕IO1 Икс[1;1]1 |
Элемент X [2; 2] в строке 2 - столбец 2 в настоящее время является целым числом = 7. Исходный происхождение индекса ⎕IO значение = 1. Таким образом, первый элемент в матрице X или X [1; 1] = 1. |
Икс[2;2]←⊂"Текст" Икс[3;4]←⊂(2 2⍴⍳4) Икс 1 2 3 4 5 6 Текст 8 9 10 11 12 13 1 2 15 3 4 16 17 18 19 20 | Элемент в X [строка 2; col 2] заменяется (с 7) на вложенный вектор «Текст» с помощью заключить ⊂ функция. Элемент в X [строка 3; col 4], ранее целое число 14, теперь становится мини закрытые или ⊂ вложенные Матрица 2x2 из 4 последовательных целых чисел. С Икс содержит числа, текст и вложенные элементы, это одновременно смешанный и вложенный множество. 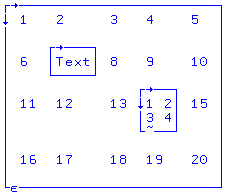 Визуальное представление вложенный массив |
Управление потоком
А Пользователь может определять индивидуальный функции которые, как и переменные, обозначаются имя а не нетекстовым символом. В заголовок функции определяет, является ли настраиваемая функция ниладической (без аргументов), монадической (один правый аргумент) или диадической (левый и правый аргументы), локальное имя результат (слева от ← назначить стрелка), и есть ли в нем какие-либо локальные переменные (каждая из которых разделена точкой с запятой ';').
| Ниладский функция PI или π (pi) | Монадический функция CIRCLEAREA | Диадический функция SEGMENTAREA, с локальными переменными |
|---|---|---|
∇ РЕЗУЛЬТАТ←ЧИСЛО ПИ РЕЗУЛЬТАТ←○1 ∇ | ∇ ПЛОЩАДЬ←CIRCLEAREA РАДИУС ПЛОЩАДЬ←ЧИСЛО ПИ×РАДИУС⋆2 ∇ | ∇ ПЛОЩАДЬ←ГРАДУСЫ СЕГМЕНТАЛЬНАЯ ЗОНА РАДИУС ; ДРОБНАЯ ЧАСТЬ ; CA ДРОБНАЯ ЧАСТЬ←ГРАДУСЫ÷360 CA←CIRCLEAREA РАДИУС ПЛОЩАДЬ←ДРОБНАЯ ЧАСТЬ×CA ∇ |
Функции с одинаковым идентификатором, но разными привязанность различны, определяется реализацией. Если разрешено, то функция CURVEAREA может быть определена дважды, чтобы заменить как монадическую CIRCLEAREA, так и диадическую SEGMENTAREA, указанную выше, при этом монадическая или диадическая функция выбирается контекстом, в котором на нее ссылаются.
Пользовательские диадические функции обычно могут применяться к параметрам с теми же соглашениями, что и встроенные функции, т.е. массивы должны либо иметь одинаковое количество элементов, либо один из них должен иметь один расширенный элемент. Есть исключения из этого, например, функция для преобразования недесятичной валюты Великобритании в доллары должна будет принимать параметр с ровно тремя элементами, представляющими фунты, шиллинги и пенсы.[11]
Внутри программы или пользовательской функции управление может быть условно передано оператору, идентифицированному номером строки или явной меткой; если целью является 0 (ноль), это завершает программу или возвращается к вызывающей функции. Наиболее распространенная форма использует функцию сжатия APL, как в шаблоне (условие) / цель, который имеет эффект оценки условия до 0 (ложь) или 1 (истина), а затем использования этого для маскировки цели (если условие false игнорируется, если true, остается в покое, поэтому управление передается).
Следовательно, функция SEGMENTAREA может быть изменена на прерывание (чуть ниже), возвращая ноль, если параметры (ГРАДУСЫ и РАДИУС ниже) равны разные знак:
∇ ПЛОЩАДЬ←ГРАДУСЫ СЕГМЕНТАЛЬНАЯ ЗОНА РАДИУС ; ДРОБНАЯ ЧАСТЬ ; CA ; ЗНАК ⍝ локальные переменные, обозначаемые точкой с запятой (;) ДРОБНАЯ ЧАСТЬ←ГРАДУСЫ÷360 CA←CIRCLEAREA РАДИУС ⍝ этот оператор кода APL вызывает пользовательскую функцию CIRCLEAREA, определенную выше. ЗНАК←(×ГРАДУСЫ)≠×РАДИУС ⍝ << ПРОВЕРКА логики APL / определение, имеют ли ГРАДУСЫ и РАДИУС НЕ (используется ≠) один и тот же ЗНАК 1-да разные (≠), 0-нет (одинаковый знак) ПЛОЩАДЬ←0 ⍝ значение по умолчанию для AREA установлено = ноль →ЗНАК/0 ⍝ разветвление (здесь выход) происходит, когда SIGN = 1, а SIGN = 0 НЕ ведет к 0. Переход к 0 завершает функцию. ПЛОЩАДЬ←ДРОБНАЯ ЧАСТЬ×CA∇Вышеупомянутая функция SEGMENTAREA работает как ожидалось, если параметры скаляры или одноэлементные массивы, но нет если они многоэлементные массивы поскольку условие в конечном итоге основывается на одном элементе массива SIGN - с другой стороны, пользовательская функция может быть изменена для правильной обработки векторизованных аргументов. Иногда работа может быть непредсказуемой, поскольку APL определяет, что компьютеры с возможностями векторной обработки должен распараллеливать и май по возможности переупорядочить операции с массивами - таким образом, тест и отладка функции пользователя особенно если они будут использоваться с векторными или даже матричными аргументами. Это влияет не только на явное применение настраиваемой функции к массивам, но и на ее использование везде, где можно разумно использовать двоичную функцию, например, при создании таблицы результатов:
90 180 270 ¯90 ∘.СЕГМЕНТАЛЬНАЯ ЗОНА 1 ¯2 40 0 00 0 00 0 00 0 0Более краткий, а иногда и лучший способ - сформулировать функцию - это избегать явной передачи управления, вместо этого использовать выражения, которые правильно оцениваются во всех или ожидаемых условиях. Иногда правильно допустить сбой функции, когда один или оба Вход аргументы неверный - именно для того, чтобы дать пользователю понять, что один или оба аргумента неверны. Следующее является более кратким, чем приведенная выше функция SEGMENTAREA. Ниже важно правильно обрабатывает векторизованные аргументы:
∇ ПЛОЩАДЬ←ГРАДУСЫ СЕГМЕНТАЛЬНАЯ ЗОНА РАДИУС ; ДРОБНАЯ ЧАСТЬ ; CA ; ЗНАК ДРОБНАЯ ЧАСТЬ←ГРАДУСЫ÷360 CA←CIRCLEAREA РАДИУС ЗНАК←(×ГРАДУСЫ)≠×РАДИУС ПЛОЩАДЬ←ДРОБНАЯ ЧАСТЬ×CA×~ЗНАК ⍝ этот оператор APL более сложен, поскольку он однострочный, но он решает векторизованные аргументы: компромисс - сложность или ветвление ∇ 90 180 270 ¯90 ∘.СЕГМЕНТАЛЬНАЯ ЗОНА 1 ¯2 40.785398163 0 12.56637061.57079633 0 25.13274122.35619449 0 37.69911180 ¯3.14159265 0Избегание явной передачи управления, также называемой ветвлением, если оно не проверено или тщательно контролируется, может способствовать использованию чрезмерно сложных один лайнер, поистине «неправильно понятые и сложные идиомы» и стиль «только для записи», который мало что сделал для того, чтобы полюбить APL влиятельным комментаторам, таким как Эдсгер Дейкстра.[12] Однако наоборот Идиомы APL могут быть интересными, образовательными и полезными, если их использовать с полезными комментарии ⍝, например, включая источник, предполагаемое значение и функцию идиомы (й). Вот Список идиом APL, Список идиом IBM APL2 здесь[13] и Библиотека финских идиом APL здесь.
Разное
| Имя (а) | Символ | Пример | Значение (примера) | Кодовая точка Unicode |
|---|---|---|---|---|
| Высокий минус[14] | ¯ | ¯3 | Обозначает отрицательное число | U + 00AF ¯ |
| Лампа, Комментарий | ⍝ | ⍝Это комментарий | Все справа от ⍝ обозначает комментарий. | U + 235D ⍝ |
| RightArrow, Branch, GoTo | → | → This_Label | → This_Label отправляет выполнение APL в This_Label: | U + 2192 → |
| Назначить, Стрелка влево, Установить в | ← | B ← A | B ← A устанавливает значения и форму B для соответствия A | U + 2190 ← |
Большинство реализаций APL поддерживают ряд системных переменных и функций, которым обычно предшествует ⎕ (четырехъядерный) и или ")" (крюк= закрывающая скобка) символ. Особенно важным и широко применяемым является ⎕IO (Происхождение индекса ), поскольку в то время как исходный IBM APL основывал свои массивы на 1, некоторые новые варианты основывают их на нуле:
| Пользовательская сессия с интерпретатором APL | Описание |
|---|---|
Икс←⍳12 Икс1 2 3 4 5 6 7 8 9 10 11 12 ⎕IO1 Икс[1]1 | Икс установить = в вектор из 12 последовательных целых чисел. Исходный происхождение индекса ⎕IO значение = 1. Таким образом, первая позиция в векторе X или X [1] = 1 на вектор значений йоты {1 2 3 4 5 ...}. |
⎕IO←0 Икс[1]2 Икс[0]1 | Происхождение индекса ⎕IO теперь изменяется на 0. Таким образом, «первая позиция индекса» в векторе X изменяется с 1 на 0. Следовательно, X [1] затем ссылается или указывает на 2 с 1 2 3 4 5 ...} и X [0] теперь ссылки 1. |
⎕WA41226371072 | Quad WA или же ⎕WA, другая динамика системная переменная, показывает, сколько осталось рабочей области неиспользованный или 41226 мегабайты или около 41 гигабайты неиспользованных имеется дополнительная общая свободная рабочая зона для рабочего пространства APL и программы для обработки с помощью. Если это число становится низким или приближается к нулю - компьютеру может потребоваться больше оперативная память (БАРАН), привод жесткого диска пробел или их комбинация для увеличения виртуальная память. |
)VARSИкс | ) VARS системная функция в APL,[15] ) VARS показывает имена пользовательских переменных, существующие в текущей рабочей области. |
Также пользователям доступны системные функции для сохранения текущего рабочего пространства, например, )СПАСТИ и завершение среды APL, например, )ВЫКЛЮЧЕННЫЙ - иногда называют крюк команды или функции из-за использования ведущей правой круглой скобки или крючка.[16] Существует некоторая стандартизация этих функций квадроцикла и крюка.
Шрифты
Юникод Базовая многоязычная плоскость включает символы APL в Разное Техническое блокировать,[17] которые, таким образом, обычно точно отображаются из более крупных шрифтов Unicode, установленных в большинстве современных операционных систем. Эти шрифты редко разрабатываются типографами, знакомыми с глифами APL. Таким образом, несмотря на точность, глифы могут показаться незнакомыми программистам APL или их трудно отличить друг от друга.
Некоторые шрифты Unicode разработаны для правильного отображения APL: APLX Upright, APL385 Unicode и SimPL.
До Unicode интерпретаторы APL поставлялись со шрифтами, в которых символы APL отображались в менее часто используемые позиции в наборах символов ASCII, обычно в верхних 128 кодовых точках. Эти сопоставления (и их национальные варианты) иногда были уникальными для интерпретатора каждого поставщика APL, что делало отображение программ APL в Интернете, в текстовых файлах и руководствах - часто проблематичным.
Функция клавиатуры APL2 для отображения символов

Обратите внимание на кнопку включения / выключения APL - крайнюю правую верхнюю клавишу, чуть ниже. Также обратите внимание, что на клавиатуре было около 55 уникальных (68 перечисленных в таблицах выше, включая сравнительные символы, но несколько символов появляются в обе монадические и диадические таблицы) Символьные клавиши APL (55 функций (операторов) APL перечислены в Справочном руководстве IBM 5110 APL), таким образом, с использованием клавиш alt, shift и ctrl - теоретически можно было бы допустить максимум некоторых 59 (ключи) *4 (при нажатии 2-х клавиш) *3 (при нажатии трех клавиш, например, ctrl-alt-del) или около 472 различных максимальных комбинаций клавиш, приближающихся к 512 EBCDIC максимум символов (256 символов умноженное на 2 кода для каждой комбинации клавиш). Опять же, теоретически клавиатура, изображенная ниже, позволяла бы активно использовать около 472 различных символов / функций APL для ввода с клавиатуры. На практике в ранних версиях использовалось только что-то грубо эквивалентен 55 специальным символам APL (без букв, цифр, знаков препинания и т. д.). Таким образом, ранний APL тогда использовал только около 11% (55/472) потенциала использования символьного языка на тот момент, исходя из ограничений на количество клавиш на клавиатуре, снова исключая числа, буквы, знаки препинания и т. Д. В другом смысле символы клавиатуры использование было близко к 100%, высокоэффективно, поскольку EBCDIC допускал только 256 различных символов и ASCII только 128.
Решение головоломок
APL оказался чрезвычайно полезным при решении математических задач, некоторые из которых описаны ниже.
Треугольник Паскаля
Брать Треугольник Паскаля, который представляет собой треугольный массив чисел, в котором числа на концах строк равны 1, а каждое из других чисел представляет собой сумму ближайших двух чисел в строке чуть выше него (вершина, 1, находится наверху) . Ниже приведена однострочная функция APL для визуального изображения треугольника Паскаля:
Паскаль←{0~¨⍨а⌽⊃⌽∊¨0,¨¨а∘!¨а←⌽⍳⍵} ⍝ Создайте однострочную пользовательскую функцию под названием Pascal Паскаль 7 ⍝ Запустите функцию Pascal для семи строк и покажите результаты ниже: 1 1 2 1 3 3 1 4 6 4 1 5 10 10 5 1 6 15 20 15 6 1 7 21 35 35 21 7Простые числа, доказательство противоречия через факторы
Определите количество простые числа (простое # - натуральное число больше 1 который не имеет положительных делителей, кроме 1 и самого себя) до некоторого числа N. Кен Айверсон приписывают следующее однострочное решение APL проблемы:
⎕CR 'Простые числа' ⍝ Показать простые числа пользовательской функции APLПростые числа←Простые числа N ⍝ Функция принимает один правый аргумент N (например, показывает простые числа для 1 ... int N)Простые числа←(2=+⌿0=(⍳N)∘.|⍳N)/⍳N ⍝ Однострочный текст Кена Айверсона Простые числа 100 ⍝ Показать все простые числа от 1 до 1002 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 ⍴Простые числа 10025 ⍝ Всего двадцать пять простых чисел в диапазоне до 100.Часто бывает необходимо изучить обратное или противоположное математическому решению (целые множители числа ): Докажите для подмножества целых чисел от 1 до 15, что они неосновной перечислив их факторы разложения. Каковы их множители, отличные от единицы (# делится на, кроме 1)?
⎕CR 'ProveNonPrime'Z←ProveNonPrime р⍝Показать все множители целого числа R, кроме 1 и самого числа,⍝ т.е. доказать непростое. Строка 'prime' возвращается для простого целого числа.Z←(0=(⍳р)|р)/⍳р ⍝ Определите все множители для целого числа R, сохраните в ZZ←(~(Z∊1,р))/Z ⍝ Удалите 1 и число как множители числа из Z.→(0=⍴Z)/ProveNonPrimeIsPrime ⍝ Если результат имеет нулевую форму, он не имеет других множителей и поэтому является простым.Z←р,(⊂«факторы (кроме 1)»),(⊂Z),⎕TCNL ⍝ Покажите число R, его множители (кроме самого 1) и символ новой строки→0 ⍝ Выполнено с функцией, если не простое числоProveNonPrimeIsPrime: Z←р,(⊂" основной"),⎕TCNL ⍝ функция переходит сюда, если число было простым ProveNonPrime ¨⍳15 ⍝ Докажите, что для каждого (¨) целых чисел от 1 до 15 (йота 15) не простые числа 1 основной 2 основной 3 основной 4 факторы(Кроме 1) 2 5 основной 6 факторы(Кроме 1) 2 3 7 основной 8 факторы(Кроме 1) 2 4 9 факторы(Кроме 1) 3 10 факторы(Кроме 1) 2 5 11 основной 12 факторы(Кроме 1) 2 3 4 6 13 основной 14 факторы(Кроме 1) 2 7 15 факторы(Кроме 1) 3 5Последовательность Фибоначчи
Создать Число Фибоначчи последовательность, где каждое последующее число в последовательности является суммой двух предыдущих:
⎕CR "Фибоначчи" ⍝ Функция отображения ФибоначчиFibonacciNum←Фибоначчи Nth;IOwas ⍝ Заголовок функции, имя функции = Фибоначчи, монадическая функция с 1 правым аргументом Nth; локальная переменная IOwas и возвращаемое число.⍝Создайте упорядоченное число Фибоначчи, где N-й - номер позиции числа Фибоначчи в последовательности. << описание функцииIOwas←⎕IO ⋄ ⎕IO←0 ⋄ FibonacciNum←↑0 1↓↑+.×/Nth/⊂2 2⍴1 1 1 0 ⋄ ⎕IO←IOwas ⍝ Чтобы эта функция работала правильно, ⎕IO необходимо установить на ноль. Фибоначчи¨⍳14 ⍝ В этом заявлении APL говорится: Создайте последовательность Фибоначчи по каждому (¨) целому числу (йота или ⍳) для целых чисел 1..14.0 1 1 2 3 5 8 13 21 34 55 89 144 233 ⍝ Сгенерированная последовательность, т.е. последовательность чисел Фибоначчи, сгенерированная интерпретатором APL.дальнейшее чтение
- Поливка, Раймонд П .; Пакин, Сандра (1975). APL: язык и его использование. Прентис-Холл. ISBN 978-0-13-038885-8.
- Reiter, Clifford A .; Джонс, Уильям Р. (1990). APL с математическим акцентом (1-е изд.). Тейлор и Фрэнсис. ISBN 978-0534128647.
- Томпсон, Норман Д.; Поливка, Раймонд П. (2013). APL2 в подробностях (серия Springer в статистике) (Мягкая обложка) (Перепечатка оригинала 1-го изд.). Springer. ISBN 978-0387942131.
- Гилман, Леонард; Роуз, Аллен Дж. (1976). А. П. Л .: Интерактивный подход (Мягкая обложка) (3-е изд.). ISBN 978-0471093046.
Смотрите также
- Разное Техническое - Блок Unicode, включая ключи APL
- APL (кодовая страница) § Раскладка клавиатуры - Более современная информация о раскладке клавиатуры APL
Рекомендации
- ^ Айверсон, Кеннет Э. (1962-01-01). «Язык программирования». Материалы весенней совместной компьютерной конференции 1–3 мая 1962 г.. AIEE-IRE '62 (весна). Нью-Йорк, Нью-Йорк, США: ACM: 345–351. Дои:10.1145/1460833.1460872.
- ^ Баронет, Дан. «Операторы Sharp APL». archive.vector.org.uk. Фото со стока - Журнал Британской ассоциации APL. Получено 13 января 2015.
- ^ MicroAPL. «Примитивные операторы». www.microapl.co.uk. MicroAPL. Получено 13 января 2015.
- ^ MicroAPL. «Операторы». www.microapl.co.uk. MicroAPL. Получено 13 января 2015.
- ^ Прогопедия. «АПЛ». progopedia.com. Прогопедия. Получено 13 января 2015.
- ^ Дьялог. «D-функции и операторы, свободно сгруппированные по категориям». dfns.dyalog.com. Дьялог. Получено 13 января 2015.
- ^ IBM. "Справочное руководство IBM 5100 APL" (PDF). bitsavers.trailing-edge.com. IBM. Архивировано из оригинал (PDF) 14 января 2015 г.. Получено 14 января 2015.
- ^ Браун, Джим (1978). «В защиту происхождения индекса 0». ACM SIGAPL APL Quote Quad. 9 (2): 7. Дои:10.1145/586050.586053.
- ^ MicroAPL. "Руководство по языку APLX" (PDF). www.microapl.co.uk. MicroAPL - версия 5. 0 июня 2009 г. с. 22. Получено 31 января 2015.
- ^ Бенкард, Дж. Филип (1992). «Вложенные массивы и операторы: некоторые проблемы в глубине». ACM SIGAPL APL Quote Quad. 23 (1): 7–21. Дои:10.1145/144045.144065. ISBN 978-0897914772.
- ^ Берри, Пол "APL 360 Primer Student Text", IBM Research, Исследовательский центр Томаса Дж. Ватсона, 1969.
- ^ "Научный труд" (PDF). www.cs.utexas.edu. Получено 2019-09-10.
- ^ Кейсон, Стэн. "Библиотека идиом APL2". www-01.ibm.com. IBM. Получено 1 февраля 2015.
- ^ «Высокий минус» APL применяется к единственному последующему числу, в то время как монадическая функция «минус» изменяет знак всего массива справа от него.
- ^ «Рабочее пространство - Системные функции». Microapl.co.uk. п. (в нижней части веб-страницы). Получено 2018-11-05.
- ^ "Справочник по языку APL" (PDF). Получено 2018-11-05.
- ^ Диаграмма Unicode «Разное техническое (включая APL)» (PDF).
внешняя ссылка
- Ссылка на символ APL: Страница 1, Страница 2, Стр. 3, Стр. 4
- Страница шрифтов Британской ассоциации APL
- Кодовая страница IBM 293 иначе кодовая страница APL на мэйнфреймы
- Общая информация о APL-символах в APL wiki
- расширение APL и его символы-операторы клавиатуры.
- Ли, Ха. "Как создать раскладку клавиатуры APL или математических символов". Получено 13 января 2015.
Общие онлайн-руководства
- Практическое введение в APL 1 и APL 2 Грэм Дональд Робертсон
- APL для ПК, серверов и планшетов - NARS полнофункциональный, без ограничений, бесплатно загружаемый APL / 2 с вложенными массивами от Sudley Place Software
- GNU APL бесплатно скачиваемый интерпретатор для APL Юргена Зауэрмана
- Руководства по YouTube APL загружено Чимином Паком, 8 вводных / обучающих видео для начинающих.
- Список скомпилированных руководств SIGAPL
- Learn APL: Учебник APL от MicroAPL
Правила синтаксиса
- Игра Конвея в жизни в APL, на YouTube
- Айверсон, Кеннет Э. (1983). «Синтаксис и семантика APL». ACM SIGAPL APL Quote Quad. 13 (3): 223–231. Дои:10.1145/800062.801221. ISBN 978-0897910958.
- Гффер, М. (1989). «Будущий APL: примеры и проблемы». ACM SIGAPL APL Quote Quad. 19 (4): 158–163. Дои:10.1145/75144.75166. ISBN 978-0897913270.
