Цветовое пространство CIE 1931 - CIE 1931 color space

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Цветовое пространство CIE 1931»  – Новости  · газеты  · книги  · ученый  · JSTOR (Май 2019) (Узнайте, как и когда удалить этот шаблон сообщения)

В Цветовые пространства CIE 1931 являются первыми определенными количественными связями между распределениями длин волн в электромагнитном видимый спектр, и физиологически воспринимаемые цвета у человека цветовое зрение. Математические отношения, которые определяют эти цветовые пространства являются важными инструментами для Управление цветом, что важно при работе с цветными чернилами, дисплеями с подсветкой и записывающими устройствами, такими как цифровые камеры. Система была разработана в 1931 г. "Международная комиссия по освещению", известный на английском языке как Международная комиссия по освещению.

В Цветовое пространство CIE 1931 RGB и Цветовое пространство CIE 1931 XYZ были созданы Международная комиссия по освещению (CIE) в 1931 году.^[1][2] Они явились результатом серии экспериментов, проведенных в конце 1920-х годов Уильямом Дэвидом Райтом с участием десяти наблюдателей.^[3] и Джон Гилд с семью наблюдателями.^[4] Экспериментальные результаты были объединены в спецификацию цветового пространства CIE RGB, из которого было получено цветовое пространство CIE XYZ.

Цветовые пространства CIE 1931 года все еще широко используются, как и цветовые пространства 1976 года. CIELUV цветовое пространство.

Трехцветные значения

Нормализованный спектральная чувствительность человека конические клетки коротковолнового, средне- и длинноволнового типов.

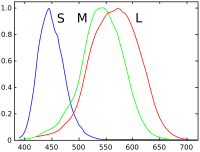
В человеческий глаз с нормальным зрением имеет три вида конические клетки этот чувственный свет, имеющий пики спектральная чувствительность короче ("S", 420 нм – 440 нм), средний ("М", 530 нм – 540 нм) и длинное ("L", 560 нм – 580 нм) длины волн. Эти клетки колбочек лежат в основе восприятия цвета человеком в условиях средней и высокой яркости; в очень тусклом свете цветовое зрение уменьшает, и монохроматические рецепторы "ночного видения" низкой яркости, обозначенные как "стержневые клетки ", становятся эффективными. Таким образом, три параметра, соответствующие уровням стимула трех видов колбочек, в принципе описывают любое цветовое ощущение человека. Взвешивание общего спектра мощности света по индивидуальной спектральной чувствительности трех видов колбочек дает три эффективные значения стимул; эти три значения составляют трехцветную характеристику объективного цвета светового спектра. Три параметра, обозначенные «S», «M» и «L», обозначены с помощью 3-х мерный пространство под названием "Цветовое пространство LMS ", которое является одним из многих цветовых пространств, разработанных для количественной оценки человеческого цветовое зрение.

Цветовое пространство отображает диапазон цветов, физически созданных из смешанного света, пигменты и т. д. к объективному описанию цветовых ощущений, регистрируемых человеческим глазом, обычно в терминах трехцветных значений, но не обычно в Цветовое пространство LMS определяется спектральной чувствительностью конические клетки. В трехцветные значения связанных с цветовым пространством, можно представить как количество трех основные цвета в трихроматическом, добавка цветовая модель. В некоторых цветовых пространствах, включая пространства LMS и XYZ, используемые основные цвета не являются настоящими цветами в том смысле, что они не могут быть созданы ни в каком световом спектре.

Цветовое пространство CIE XYZ охватывает все цветовые ощущения, видимые человеку со средним зрением. Вот почему CIE XYZ (трехцветные значения) представляет собой аппаратно-инвариантное представление цвета.^[5] Он служит стандартным справочником, по которому определяются многие другие цветовые пространства. Набор функций согласования цветов, таких как кривые спектральной чувствительности Цветовое пространство LMS, но не ограничиваясь неотрицательной чувствительностью, связывает физически создаваемые световые спектры с определенными трехцветными значениями.

Рассмотрим два источника света, состоящих из разных смесей с разными длинами волн. Такие источники света могут быть одного цвета; этот эффект именуется "метамерия ". Такие источники света имеют одинаковый видимый цвет для наблюдателя, когда они производят одинаковые трехцветные значения, независимо от спектральные распределения мощности источников.

Большинство длин волн стимулируют два или все три вида конусная ячейка потому что кривые спектральной чувствительности трех типов перекрываются. Таким образом, определенные трехцветные значения физически невозможны, например, трехцветные значения LMS, которые не равны нулю для компонента M и равны нулю для компонентов L и S. Кроме того, трехцветные значения LMS для чистых спектральных цветов будут в любом нормальном трехцветном аддитивном цветовом пространстве, например. грамм. в Цветовые пространства RGB, подразумевают отрицательные значения хотя бы для одного из трех праймериз поскольку цветность будет за пределами цветной треугольник определяется основными цветами. Чтобы избежать этих отрицательных значений RGB и иметь один компонент, описывающий воспринимаемое яркость сформулированы «мнимые» основные цвета и соответствующие функции согласования цветов. Цветовое пространство CIE 1931 определяет результирующие трехцветные значения, в которых они обозначаются буквами «X», «Y» и «Z».^[6] В пространстве XYZ все комбинации неотрицательных координат имеют смысл, но многие из них, такие как основные местоположения [1, 0, 0], [0, 1, 0] и [0, 0, 1], соответствуют воображаемые цвета вне пространства возможных координат LMS; воображаемые цвета не соответствуют какому-либо спектральному распределению длин волн и, следовательно, не имеют физической реальности.

Значение Икс, Y и Z

Сравнение типичной нормализованной спектральной чувствительности M-конуса и CIE 1931 функция светимости для стандартного наблюдателя в фотопическое зрение.

При оценке родственника яркость (яркость) разных цветов в хорошо освещенных ситуациях люди склонны воспринимать свет в зеленой части спектра как более яркий, чем красный или синий свет равной мощности. В функция светимости который описывает воспринимаемую яркость различных длин волн, таким образом, примерно аналогичен спектральной чувствительности M колбочек.

Модель CIE использует этот факт, устанавливая Y как яркость. Z квазиравно синему или S-конусу, и Икс представляет собой смесь кривых отклика, выбранных как неотрицательные. Значения тристимула XYZ, таким образом, аналогичны ответам конуса LMS человеческого глаза, но отличаются от них. Параметр Y поскольку яркость дает полезный результат, который для любого заданного Y значение, плоскость XZ будет содержать все возможные цветности при такой яркости.

Единица трехцветных значений Икс, Y, и Z часто выбирается произвольно, так что Y = 1 или же Y = 100 самый яркий белый цвет, поддерживаемый цветным дисплеем. В этом случае значение Y известно как относительная яркость. Соответствующие значения белой точки для Икс и Z затем можно вывести, используя стандартные источники света.

Стандартный наблюдатель CIE

Из-за распределения колбочек в глазу значения цветового стимула зависят от наблюдателя. поле зрения. Чтобы исключить эту переменную, CIE определил функцию сопоставления цветов, называемую стандартный (колориметрический) наблюдатель, чтобы представить средний хроматический отклик человека в пределах дуги 2 ° внутри ямка. Этот угол был выбран из-за того, что чувствительные к цвету колбочки располагались в пределах дуги 2 ° от ямки. Таким образом Стандартный наблюдатель CIE 1931 функция также известна как CIE 1931 2 ° Стандартный наблюдатель. Более современная, но менее используемая альтернатива - это CIE 1964 10 ° Стандартный наблюдатель, который заимствован из работ Стайлза и Берча,^[7] и Сперанская.^[8]

Для экспериментов с углом 10 ° наблюдателям было дано указание игнорировать центральное пятно 2 °. Функция дополнительного стандартного наблюдателя 1964 года рекомендуется при работе с полем зрения более 4 °. Обе стандартные функции наблюдателя дискретизируются на 5 нм интервалы длин волн от 380 нм к 780 нм и распространяется CIE.^[9] А 1 нм-интервальный набор данных, очевидно, часть публикации CIE 1986 г., также доступен.^{[нужна цитата ]} Все соответствующие значения были рассчитаны из экспериментально полученных данных с использованием интерполяция. Стандартный наблюдатель характеризуется тремя функции согласования цветов.

Приводится вывод стандартного наблюдателя CIE из экспериментов по подбору цветов. ниже, после описания пространства CIE RGB.

Функции согласования цветов

Стандартные функции согласования цвета наблюдателя CIE XYZ

Функции согласования цветов CIE RGB

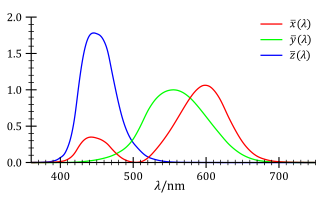
CIE функции согласования цветов ${ displaystyle { overline {x}} ( lambda)}$, ${ displaystyle { overline {y}} ( lambda)}$ и ${ displaystyle { overline {z}} ( lambda)}$ являются численным описанием хроматической характеристики наблюдатель (описано выше). Их можно рассматривать как кривые спектральной чувствительности трех линейных детекторов света, дающие трехцветные значения CIE. Икс, Y и Z. В совокупности эти три функции описывают стандартный наблюдатель CIE.^[10]

Аналитическое приближение

Поиск в таблице может стать непрактичным для некоторых вычислительных задач. Вместо ссылки на опубликованную таблицу функции согласования цветов CIE XYZ могут быть аппроксимированы суммой Гауссовы функции,^[11] следующее:

Позволять грамм(Икс) обозначают кусочно-гауссову функцию, определяемую формулой

${ Displaystyle г (х; альфа, му, сигма _ {1}, сигма _ {2}) = альфа ехр влево ({ гидроразрыва {(х- му) ^ {2}} {-2 sigma ^ {2}}} right), { text {where}} sigma = { begin {cases} sigma _ {1}, & x < mu, sigma _ {2 }, & x geq mu. end {case}}}$

То есть, грамм(Икс) напоминает колоколообразную кривую с пиком на Икс = μ, спред / стандартное отклонение σ₁ слева от среднего, разброс σ₂ справа от среднего, а параметр масштабирования α. С длиной волны λ измеряется в ангстремы, мы затем аппроксимируем функции согласования цветов 1931 года следующим образом:

${ displaystyle { begin {align} { overline {x}} ( lambda) & = g ( lambda; 1.056,5998,379,310) + g ( lambda; 0,362,4420,160,267) + g ( lambda ; -0,065,5011,204,262), { overline {y}} ( lambda) & = g ( lambda; 0,821,5688,469,405) + g ( lambda; 0,286,5309,163,311), { overline {z}} ( lambda) & = g ( lambda; 1.217,4370,118,360) + g ( lambda; 0,681,4590,260,138). end {выравнивается}}}$

Это приближение может быть легко использовано в языке программирования в функциональном стиле. Например, вот такой Haskell выполнение:

xyzOfWavelength λ = карта (сумма . карта грамм)  [ [ (1056,5998,379,310), (362,4420,160,267), (-65,5011,204,262) ]  , [ ( 821,5688,469,405), (286,5309,163,311) ]  , [ (1217,4370,118,360), (681,4590,260,138) ]  ]  куда грамм(α,μ,σ1,σ2) = α/1000 * exp(-((λ-μ)/(если λ<μ тогда σ1 еще σ2))^2 / 2)

Вот реализация полуфункционального стиля в C:

двойной гауссовский(двойной Икс, двойной альфа, двойной му, двойной сигма1, двойной сигма2) {  двойной квадратный корень = (Икс - му)/(Икс < му ? сигма1 : сигма2);  возвращаться альфа * exp( -(квадратный корень * квадратный корень)/2 );}пустота xyzFromWavelength(двойной* xyz, двойной длина волны) {  xyz[0] = гауссовский(длина волны,  1.056, 5998, 379, 310)         + гауссовский(длина волны,  0.362, 4420, 160, 267)         + гауссовский(длина волны, -0.065, 5011, 204, 262);  xyz[1] = гауссовский(длина волны,  0.821, 5688, 469, 405)         + гауссовский(длина волны,  0.286, 5309, 163, 311);  xyz[2] = гауссовский(длина волны,  1.217, 4370, 118, 360)         + гауссовский(длина волны,  0.681, 4590, 260, 138);}

Существуют и другие аналитические подходы, но ни один из них не работает так хорошо, как здесь (по состоянию на июль 2013 г.). Также можно использовать меньшее количество гауссовских функций, с одним гауссовым значением для каждой «доли». CIE 1964 хорошо сочетается с однополюсной функцией.^[11]

Функции согласования цветов CIE XYZ неотрицательны и приводят к неотрицательным координатам XYZ для всех реальных цветов (то есть для неотрицательных световых спектров). Другие наблюдатели, например, для пространства CIE RGB или других Цветовые пространства RGB, определяются другими наборами из трех функций сопоставления цветов, обычно не неотрицательными, и приводят к значениям трехцветных цветов в этих других пространствах, которые могут включать отрицательные координаты для некоторых реальных цветов.

Вычисление XYZ из спектральных данных

Эмиссионный футляр

Значения трехцветного цвета для цвета с спектральное сияние L_{е, Ω, λ} даны в терминах стандартного наблюдателя:

${ displaystyle X = int _ { lambda} L _ { mathrm {e}, Omega, lambda} ( lambda) , { overline {x}} ( lambda) , d lambda,}$

${ displaystyle Y = int _ { lambda} L _ { mathrm {e}, Omega, lambda} ( lambda) , { overline {y}} ( lambda) , d lambda,}$

${ displaystyle Z = int _ { lambda} L _ { mathrm {e}, Omega, lambda} ( lambda) , { overline {z}} ( lambda) , d lambda.}$

куда ${ displaystyle lambda}$ длина волны эквивалентного монохромный свет (измеряется в нанометры ), а обычные пределы интеграла равны ${ displaystyle lambda in [380 780]}$.

Ценности Икс, Y, и Z ограничены, если спектр яркости L_{е, Ω, λ} ограничено.

Светоотражающие и пропускающие футляры

Отражающий и пропускающий футляры очень похожи на эмиссионный, с некоторыми отличиями. Спектральное сияние L_{е, Ω, λ} заменяется спектральным отражательная способность (или же коэффициент пропускания ) S (λ) измеряемого объекта, умноженное на спектральное распределение мощности источника света I (λ).

${ Displaystyle X = { гидроразрыва {K} {N}} int _ { lambda} S ( lambda) , I ( lambda) , { overline {x}} ( lambda) , d lambda,}$

${ displaystyle Y = { frac {K} {N}} int _ { lambda} S ( lambda) , I ( lambda) , { overline {y}} ( lambda) , d lambda,}$

${ displaystyle Z = { frac {K} {N}} int _ { lambda} S ( lambda) , I ( lambda) , { overline {z}} ( lambda) , d lambda,}$

куда

${ displaystyle N = int _ { lambda} I ( lambda) , { overline {y}} ( lambda) , d lambda,}$

K - коэффициент масштабирования (обычно 1 или 100), и ${ displaystyle lambda}$ длина волны эквивалентного монохромный свет (измеряется в нанометры ), а стандартные пределы интеграла равны ${ displaystyle lambda in [380 780]}$.

Диаграмма цветности CIE xy и цветовое пространство CIE xyY

Диаграмма цветности цветового пространства CIE 1931. Внешняя криволинейная граница - это спектральный (или монохроматический) локус с длинами волн, показанными в нанометрах. Обратите внимание, что цвета, отображаемые на экране на этом изображении, указаны с помощью sRGB, поэтому цвета за пределами sRGB гамма не отображаются должным образом. В зависимости от цветовое пространство и калибровка устройства отображения, цвета sRGB также могут отображаться неправильно. На этой диаграмме показаны максимально насыщенные яркие цвета, которые может дать компьютерный монитор или же телевизор.

Диаграмма цветности цветового пространства CIE 1931, отображаемая в терминах цветов с более низкой насыщенностью и значением, чем те, которые показаны на диаграмме выше, которые могут быть получены с помощью пигменты, например, используемые в печать. Названия цветов взяты из Цветовая система Манселла. Сплошная кривая с точками посередине - это Планковский локус, с точками, соответствующими нескольким выбранным черное тело температуры, которые указаны чуть выше оси абсцисс.

Поскольку человеческий глаз имеет три типа датчиков цвета, которые реагируют на разные диапазоны длины волн, полный график всех видимых цветов представляет собой трехмерную фигуру. Однако понятие цвета можно разделить на две части: яркость и цветность. Например, белый цвет - это яркий цвет, а серый цвет считается менее яркой версией того же белого цвета. Другими словами, цветность белого и серого одинакова, а их яркость различается.

Цветовое пространство CIE XYZ было специально разработано таким образом, чтобы Y параметр является мерой яркость цвета. Затем цветность определяется двумя производными параметрами. Икс и у, два из трех нормированных значений являются функциями всех трех трехцветные значения Икс, Y, и Z: ^[12]

${ Displaystyle х = { гидроразрыва {X} {X + Y + Z}}}$

${ displaystyle y = { frac {Y} {X + Y + Z}}}$

${ displaystyle z = { frac {Z} {X + Y + Z}} = 1-x-y}$

Производное цветовое пространство, указанное Икс, у, и Y называется цветовым пространством CIE xyY и широко используется для определения цветов на практике.

В Икс и Z значения цветности могут быть рассчитаны на основе значений цветности Икс и у и Y трехцветное значение: ^[13]

${ displaystyle X = { frac {Y} {y}} x,}$

${ displaystyle Z = { frac {Y} {y}} (1-x-y).}$

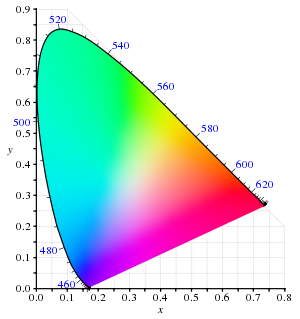
На рисунке справа показана соответствующая диаграмма цветности. Внешняя кривая граница - это спектральный локус, с длинами волн, указанными в нанометрах. Обратите внимание, что диаграмма цветности - это инструмент, позволяющий определить, как человеческий глаз будет воспринимать свет с заданным спектром. Он не может указывать цвета объектов (или печатных красок), поскольку цветность, наблюдаемая при взгляде на объект, также зависит от источника света.

Математически цвета диаграммы цветности занимают область реальная проективная плоскость.

Диаграмма цветности иллюстрирует ряд интересных свойств цветового пространства CIE XYZ:

• На диаграмме представлены все цветности, видимые среднему человеку. Они показаны цветом, и эта область называется гамма человеческого зрения. Палитра всех видимых цветностей на графике CIE представляет собой фигуру в форме языка или подковы, показанную цветом. Изогнутый край гаммы называется спектральный локус и соответствует монохроматическому свету (каждая точка представляет собой чистый оттенок одной длины волны), причем длины волн указаны в нанометрах. Прямая кромка в нижней части гаммы называется линия пурпурных. Эти цвета, хотя и находятся на границе гаммы, не имеют аналогов в монохроматическом свете. Менее насыщенные цвета появляются внутри фигуры с белым в центре.
• Видно, что все видимые цветности соответствуют неотрицательным значениям Икс, у, и z (и, следовательно, к неотрицательным значениям Икс, Y, и Z).
• Если выбрать любые две точки цвета на диаграмме цветности, тогда все цвета, которые лежат на прямой линии между двумя точками, могут быть сформированы путем смешивания этих двух цветов. Отсюда следует, что цветовая гамма должна быть выпуклый в форме. Все цвета, которые могут быть сформированы путем смешивания трех источников, находятся внутри треугольника, образованного точками источников на диаграмме цветности (и так далее для нескольких источников).
• Равная смесь двух одинаково ярких цветов, как правило, не находится в середине этого отрезок. В более общем плане расстояние на диаграмме цветности CIE xy не соответствует степени различия между двумя цветами. В начале 1940-х гг. Дэвид МакАдам изучил природу зрительной чувствительности к цветовые различия, и суммировал свои результаты в концепции Эллипс макадама. Основываясь на работе MacAdam, CIE 1960, CIE 1964, и CIE 1976 цветовые пространства были разработаны с целью достижения единообразия восприятия (одинаковые расстояния в цветовом пространстве соответствуют одинаковым различиям в цвете). Хотя они были явным улучшением по сравнению с системой CIE 1931, они не были полностью свободны от искажений.
• Можно видеть, что, учитывая три реальных источника, эти источники не могут охватывать весь спектр человеческого зрения. С геометрической точки зрения в пределах гаммы нет трех точек, которые образуют треугольник, включающий всю гамму; или, проще говоря, диапазон человеческого зрения - это не треугольник.
• Свет с плоский спектр мощности по длине волны (равная мощность в каждом 1 нм интервал) соответствует точке (Икс, у) = (1/3, 1/3).

Смешивание цветов, указанных на диаграмме цветности CIE xy

Когда два или более цвета аддитивно смешиваются, координаты цветности x и y результирующего цвета (x_{смешивание}, y_{смешивание}) может быть рассчитана по цветности компонентов смеси (x₁, y₁; Икс₂, y₂; …; Икс_п, y_п) и соответствующие им яркости (L₁, L₂,…, L_п) по следующим формулам:^[14]

$${ displaystyle x _ { mathrm {mix}} = { frac {{ dfrac {x_ {1}} {y_ {1}}} L_ {1} + { dfrac {x_ {2}} {y_ {2}} {y_ {2}) }}} L_ {2} + dots + { dfrac {x_ {n}} {y_ {n}}} L_ {n}} {{ dfrac {L_ {1}} {y_ {1}}} + { dfrac {L_ {2}} {y_ {2}}} + dots + { dfrac {L_ {n}} {y_ {n}}}}} quad, quad y _ { mathrm {mix} } = { frac {L_ {1} + L_ {2} + dots + L_ {n}} {{ dfrac {L_ {1}} {y_ {1}}} + { dfrac {L_ {2}) } {y_ {2}}} + dots + { dfrac {L_ {n}} {y_ {n}}}}}}$$

Эти формулы могут быть получены из ранее представленных определений координат цветности x и y, используя тот факт, что значения цветности X, Y и Z отдельных компонентов смеси являются непосредственно аддитивными. Вместо значений яркости (L₁, L₂и т. д.) в качестве альтернативы можно использовать любую другую фотометрическую величину, которая прямо пропорциональна трехцветному значению Y (что, естественно, означает, что сам Y также может быть использован).

Как уже упоминалось, при смешивании двух цветов полученный цвет x_{смешивание}, y_{смешивание} будет лежать на отрезке прямой линии, который соединяет эти цвета на диаграмме цветности CIE xy. Для расчета соотношения смешивания компонентов цветов x₁, y₁ и х₂, y₂ что приводит к определенному x_{смешивание}, y_{смешивание} на этом отрезке прямой можно использовать формулу

$${ displaystyle { frac {L_ {1}} {L_ {2}}} = { frac {y_ {1} left (x_ {2} -x _ { mathrm {mix}} right)} {y_ {2} left (x _ { mathrm {mix}} -x_ {1} right)}} = { frac {y_ {1} left (y_ {2} -y _ { mathrm {mix}} right)} {y_ {2} left (y _ { mathrm {mix}} -y_ {1} right)}}}$$

где L₁ это яркость цвета x₁, y₁ и я₂ яркость цвета x₂, y₂. Обратите внимание: поскольку y_{смешивание} однозначно определяется x_{смешивание} и наоборот, зная только один из них, достаточно для расчета соотношения смешивания. Также отметим, что в соответствии с замечаниями к формулам для x_{смешивание} и у_{смешивание}, соотношение смешивания L₁/ Л₂ вполне может быть выражен через другие фотометрические величины, кроме яркости.

Определение цветового пространства CIE XYZ

Цветовое пространство CIE RGB

Цветовое пространство CIE RGB - одно из многих Цветовые пространства RGB, отличающиеся особым набором монохроматических (одноволновых) основные цвета.

В 1920-х годах У. Дэвид Райт провел два независимых эксперимента по восприятию цвета людьми.^[3] с десятью наблюдателями, и Джон Гилд^[4] с семью наблюдателями. Их результаты заложили основу для спецификации трехцветного цветового пространства CIE XYZ.

Диапазон основных цветов CIE RGB и расположение основных цветов на CIE 1931 ху диаграмма цветности.

Эксперименты проводились с использованием круглого разделенного экрана (двудольного поля) диаметром 2 градуса, что соответствует угловому размеру человеческого тела. ямка. С одной стороны тест проецировался цвет, а на другой - цвет, регулируемый наблюдателем. Регулируемый цвет представлял собой смесь трех начальный цвета, каждый с фиксированным цветность, но с регулируемым яркость.

Наблюдатель будет изменять яркость каждого из трех основных лучей до тех пор, пока не будет наблюдаться совпадение с тестовым цветом. Не все тестовые цвета можно было сопоставить с помощью этой техники. В этом случае к тестируемому цвету можно было добавить переменное количество одного из основных цветов, и сопоставление с двумя оставшимися основными цветами проводилось с помощью переменного цветового пятна. В этих случаях количество первичного добавленного к тестируемому цвету считалось отрицательным. Таким образом можно было охватить весь диапазон цветового восприятия человека. Когда тестовые цвета были монохроматическими, можно было построить график количества каждого основного цвета в зависимости от длины волны тестового цвета. Эти три функции называются функции согласования цветов для этого конкретного эксперимента.

Функции согласования цветов CIE 1931 RGB. Функции согласования цветов - это количество основных цветов, необходимое для согласования с монохроматическим тестовым цветом на длине волны, показанной на горизонтальной шкале.

Хотя эксперименты Райта и Гилда проводились с использованием различных основных цветов при разной интенсивности, и хотя они использовали несколько разных наблюдателей, все их результаты были суммированы с помощью стандартных функций сопоставления цветов CIE RGB. ${ displaystyle { overline {r}} ( lambda)}$, ${ displaystyle { overline {g}} ( lambda)}$, и ${ displaystyle { overline {b}} ( lambda)}$, полученные с использованием трех монохроматических основных цветов на стандартизованных длинах волн 700 нм (красный), 546,1 нм (зеленый) и 435,8 нм (синий). Функции согласования цветов - это количество первичных цветов, необходимых для согласования первичных цветов монохроматического теста. Эти функции показаны на графике справа (CIE 1931). Обратите внимание, что ${ displaystyle { overline {r}} ( lambda)}$ и ${ displaystyle { overline {g}} ( lambda)}$ равны нулю в 435,8 нм, ${ displaystyle { overline {r}} ( lambda)}$ и ${ displaystyle { overline {b}} ( lambda)}$ равны нулю в 546,1 нм и ${ displaystyle { overline {g}} ( lambda)}$ и ${ displaystyle { overline {b}} ( lambda)}$ равны нулю в 700 нм, поскольку в этих случаях тестовый цвет является одним из основных. Основные цвета с длинами волн 546,1 нм и 435,8 нм были выбраны потому, что они представляют собой легко воспроизводимые монохроматические линии разряда паров ртути. В 700 нм Длина волны, которую в 1931 году было трудно воспроизвести в качестве монохроматического луча, была выбрана потому, что восприятие цвета глазом на этой длине волны довольно не меняется, и поэтому небольшие ошибки в длине волны этой первичной обмотки мало повлияют на результаты.

Функции согласования цветов и основные цвета были определены специальной комиссией CIE после значительных размышлений.^[15] Отсечки на коротковолновой и длинноволновой сторонах диаграммы выбраны несколько произвольно; человеческий глаз действительно может видеть свет с длинами волн примерно до 810 нм, но с чувствительностью во много тысяч раз ниже, чем для зеленого света. Эти функции согласования цветов определяют так называемый «стандартный наблюдатель 1931 CIE». Обратите внимание, что вместо того, чтобы указывать яркость каждого основного цвета, кривые нормализуются, чтобы иметь постоянную площадь под ними. Эта область фиксируется на определенном значении, указав, что

${ displaystyle int _ {0} ^ { infty} { overline {r}} ( lambda) , d lambda = int _ {0} ^ { infty} { overline {g}} ( lambda) , d lambda = int _ {0} ^ { infty} { overline {b}} ( lambda) , d lambda.}$

Полученные в результате нормализованные функции согласования цветов затем масштабируются в соотношении r: g: b 1: 4,5907: 0,0601 для источника. яркость и 72.0962: 1.3791: 1 для источника сияние для воспроизведения истинных функций согласования цветов. Предлагая стандартизировать основные цвета, CIE установил международную систему объективной цветовой нотации.

Учитывая эти масштабированные функции согласования цветов, RGB трехцветный оценивает цвет с помощью спектральное распределение мощности ${ Displaystyle S ( lambda)}$ тогда будет дано:

${ Displaystyle R = int _ {0} ^ { infty} S ( lambda) , { overline {r}} ( lambda) , d lambda,}$

${ Displaystyle G = int _ {0} ^ { infty} S ( lambda) , { overline {g}} ( lambda) , d lambda,}$

${ displaystyle B = int _ {0} ^ { infty} S ( lambda) , { overline {b}} ( lambda) , d lambda.}$

Это все внутренние продукты и может рассматриваться как проекция бесконечномерного спектра на трехмерный цвет.

Закон Грассмана

Кто-то может спросить: «Почему возможно, что результаты Райта и Гилда могут быть суммированы с использованием различных основных цветов и интенсивности, отличных от фактически используемых?» Можно также спросить: «А как насчет случая, когда сравниваемые тестовые цвета не являются монохроматическими?» Ответ на оба эти вопроса заключается в (почти) линейности человеческого восприятия цвета. Эта линейность выражается в Закон Грассмана.

Пространство CIE RGB можно использовать для определения цветности обычным способом: координаты цветности р, грамм и б куда:

${ displaystyle r = { frac {R} {R + G + B}},}$

${ displaystyle g = { frac {G} {R + G + B}},}$

${ displaystyle b = { frac {B} {R + G + B}}.}$

Построение цветового пространства CIE XYZ на основе данных Райта – Гильдии

Воспроизвести медиа

Воспроизвести медиа

В sRGB гамма (оставили) и видимой гамме при освещении D65 (верно) проецируется в цветовом пространстве CIEXYZ. Икс и Z - горизонтальные оси; Y - вертикальная ось.

Воспроизвести медиа

Воспроизвести медиа

В sRGB гамма (оставили) и видимой гамме при освещении D65 (верно) проецируется в цветовом пространстве CIExyY. Икс и у - горизонтальные оси; Y - вертикальная ось.

Разработав модель человеческого зрения RGB с использованием функций согласования CIE RGB, члены специальной комиссии хотели разработать другое цветовое пространство, которое будет иметь отношение к цветовому пространству CIE RGB. Предполагалось, что закон Грассмана выполняется, и новое пространство будет связано с пространством CIE RGB посредством линейного преобразования. Новое пространство будет определяться с помощью трех новых функций сопоставления цветов.${ displaystyle { overline {x}} ( lambda)}$, ${ displaystyle { overline {y}} ( lambda)}$, и ${ displaystyle { overline {z}} ( lambda)}$ как описано выше. Новое цветовое пространство будет выбрано так, чтобы иметь следующие желаемые свойства:

Схема в CIE rg пространство цветности, показывающее построение треугольника, определяющего цветовое пространство CIE XYZ. Треугольник C_б-C_грамм-C_р это просто ху = (0, 0), (0, 1), (1, 0) треугольник в CIE ху пространство цветности. Линия, соединяющая C_б и C_р это алычне. Обратите внимание, что спектральный локус проходит через rg = (0, 0) в 435,8 нм, через rg = (0, 1) в 546,1 нм и через rg = (1, 0) в 700 нм. Кроме того, точка равной энергии (E) находится в rg = ху = (1/3, 1/3).

1. Новые функции согласования цветов должны были быть везде больше или равны нулю. В 1931 году вычисления производились вручную или с помощью логарифмической линейки, и указание положительных значений было полезным упрощением вычислений.
2. В ${ displaystyle { overline {y}} ( lambda)}$ функция сопоставления цветов будет точно равна фотопическая функция светоотдачи V(λ) для "стандартного фотонаблюдателя CIE".^[16] Функция яркости описывает изменение воспринимаемой яркости в зависимости от длины волны. Тот факт, что функция яркости может быть построена путем линейной комбинации функций согласования цветов RGB, никоим образом не гарантировался, но можно было ожидать, что это будет почти верным из-за почти линейной природы человеческого зрения. Опять же, основной причиной этого требования было упрощение вычислений.
3. Для постоянной энергии белая точка, требовалось, чтобы Икс = у = z = 1/3.
4. В силу определения цветность и требование положительных значений Икс и у, видно, что гамма всех цветов будет лежать внутри треугольника [1, 0], [0, 0], [0, 1]. Требовалось, чтобы гамма заполняла это пространство практически полностью.
5. Было обнаружено, что ${ displaystyle { overline {z}} ( lambda)}$ функция сопоставления цветов может быть установлена ​​на ноль выше 650 нм при этом оставаясь в пределах экспериментальной ошибки. Для простоты вычислений было указано, что это будет так.

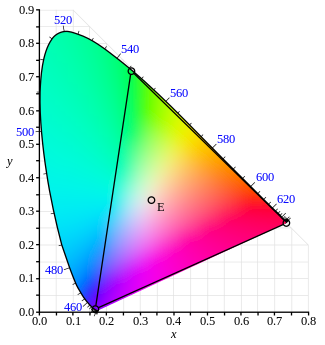
С геометрической точки зрения выбор нового цветового пространства означает выбор нового треугольника в rg пространство цветности. На рисунке вверху справа rg Координаты цветности показаны на двух осях черным цветом вместе с охватом стандартного наблюдателя 1931 года. Красным цветом показаны CIE ху оси цветности, которые определялись указанными выше требованиями. Требование неотрицательности координат XYZ означает, что треугольник, образованный C_р, С_грамм, С_б должен охватывать весь спектр стандартного наблюдателя. Линия, соединяющая C_р и C_б фиксируется требованием, чтобы ${ displaystyle { overline {y}} ( lambda)}$ функция будет равна функции яркости. Эта линия является линией нулевой яркости и называется алычне. Требование, чтобы ${ displaystyle { overline {z}} ( lambda)}$ функция быть нулевой выше 650 нм означает, что линия, соединяющая C_грамм и C_р должна касаться гаммы в области K_р. Это определяет местоположение точки C_р. Требование, чтобы точка равной энергии определялась формулой Икс = у = 1/3 накладывает ограничение на линию, соединяющую C_б и C_грамми, наконец, требование о том, что цветовая гамма заполняет пространство, накладывает второе ограничение на эту строку, чтобы она была очень близка к цветовой гамме в зеленой области, которая определяет расположение C_грамм и C_б. Вышеописанное преобразование - это линейное преобразование из пространства CIE RGB в пространство XYZ. Стандартное преобразование, принятое специальной комиссией CIE, было следующим:

Числа в приведенной ниже матрице преобразования являются точными, с количеством цифр, указанным в стандартах CIE.^[15]

${ displaystyle { begin {bmatrix} X Y Z end {bmatrix}} = { frac {1} {b_ {21}}} { begin {bmatrix} b_ {11} & b_ {12} & b_ {13} b_ {21} & b_ {22} & b_ {23} b_ {31} & b_ {32} & b_ {33} end {bmatrix}} { begin {bmatrix} R G B end {bmatrix}} = { frac {1} {0.176 , 97}} { begin {bmatrix} 0.490 , 00 & 0.310 , 00 & 0.200 , 00 0.176 , 97 & 0.812 , 40 & 0,010 , 63 0,000 , 00 & 0,010 , 00 & 0,990 , 00 end {bmatrix}} { begin {bmatrix} R G B end {bmatrix}}}$

Хотя приведенная выше матрица точно указана в стандартах, в другом направлении используется обратная матрица, которая точно не указана, но приблизительно равна:

${ displaystyle { begin {bmatrix} R G B end {bmatrix}} = { begin {bmatrix} 0,418 , 47 & -0,158 , 66 & -0,082 , 835 - 0,091 , 169 & 0 .252 , 43 & 0,015 , 708 0,000 , 920 , 90 & -0,002 , 549 , 8 & 0,178 , 60 end {bmatrix}} cdot { begin {bmatrix} X Y Z end {bmatrix}}}$

Интегралы функций согласования цвета XYZ должны быть равны согласно требованию 3 выше, и это устанавливается интегралом функции световой эффективности фотопического изображения согласно требованию 2 выше. Табличные кривые чувствительности имеют определенную произвольность. Формы личности Икс, Y и Z Кривые чувствительности можно измерить с разумной точностью. Однако общая кривая яркости (которая на самом деле представляет собой взвешенную сумму этих трех кривых) является субъективной, поскольку она включает в себя вопрос испытуемого, имеют ли два источника света одинаковую яркость, даже если они совершенно разных цветов. Аналогичным образом, относительные величины Икс, Y, и Z кривые произвольные. Кроме того, можно определить допустимое цветовое пространство с помощью Икс кривая чувствительности с удвоенной амплитудой. Это новое цветовое пространство будет иметь другую форму. Кривые чувствительности в цветовых пространствах CIE 1931 и 1964 XYZ масштабируются, чтобы иметь равные площади под кривыми.

Смотрите также

• Трихроматия
• Невозможный цвет
• Цветовое пространство CIELAB
• Стандартный источник света, определение точки белого, используемое CIE и обычно показываемое на диаграммах цветового пространства как E, D50 или D65

Рекомендации

дальнейшее чтение

• Бродбент, Артур Д. (август 2004 г.). «Критический обзор развития функций согласования цветов CIE1931 RGB». Исследование и применение цвета. 29 (4): 267–272. Дои:10.1002 / col.20020. В данной статье описывается разработка координат цветности CIE1931 и функций согласования цветов, исходя из исходных экспериментальных данных W. D. Wright и J. Guild. Дается достаточно информации, чтобы позволить читателю воспроизвести и проверить результаты, полученные на каждом этапе вычислений, и критически проанализировать используемые процедуры. К сожалению, некоторая информация, необходимая для преобразования координат, так и не была опубликована, и в прилагаемых таблицах представлены вероятные версии этих недостающих данных.
• Трезона, Пэт В. (2001). «Вывод 1964 CIE 10 ° XYZ функций согласования цветов и их применимость в фотометрии». Исследование и применение цвета. 26 (1): 67–75. Дои:10.1002 / 1520-6378 (200102) 26: 1 <67 :: AID-COL7> 3.0.CO; 2-4.
• Райт, Уильям Дэвид (2007). «Золотой юбилей цвета в CIE - Историческая и экспериментальная подоплека системы колориметрии CIE 1931 года». В Шанда, Янош (ред.). Колориметрия. Wiley Interscience. С. 9–24. Дои:10.1002 / 9780470175637.ch2. ISBN  978-0-470-04904-4. (первоначально опубликовано Общество красильщиков и колористов, Брэдфорд, 1981.)

внешняя ссылка

• Введение в цветоведение, Уильям Эндрю Стир.
• Отчет лаборатории по диаграммам цветности efg и Исходный код Delphi
• Цветовое пространство CIE, Гернот Хоффманн
• Аннотированные загружаемые таблицы данных, Эндрю Стокман и Линдси Т. Шарп.
• Расчет на основе исходных экспериментальных данных координат спектральной цветности стандартного наблюдателя CIE 1931 RGB и функций согласования цветов
• Колориметрические данные, полезные для расчетов, в различных форматах файлов
• Colorlab Набор инструментов MATLAB для вычисления науки о цвете и точной цветопередачи (от Хесуса Мало и Марии Хосе Луке, Университет Валенсии). Он включает в себя стандартную трехцветную колориметрию CIE и преобразования ряда нелинейных моделей внешнего вида цвета (CIE Lab, CIE CAM и т. Д.).
• Точная передача цвета Konica Minolta Sensing
• CIE 1931 и объяснение светодиодного биннинга, База эдафических научных знаний
• Измерение цвета в мире света Адмеси, передовые системы измерения