Эффект Яна – Теллера - Википедия - Jahn–Teller effect
В Эффект Яна – Теллера (Эффект JT или JTE) - важный механизм спонтанное нарушение симметрии в молекулярных и твердотельных системах, что имеет далеко идущие последствия в различных областях и является причиной множества явлений в спектроскопия, стереохимия, кристаллохимия, молекулярные и физика твердого тела, и материаловедение. Эффект назван в честь Герман Артур Ян и Эдвард Теллер, который впервые сообщил об этом в 1937 году. Эффект Яна-Теллера и связанный с ним Эффект Реннера-Теллера, обсуждаются в разделе 13.4 учебника по спектроскопии Банкера и Йенсена.[1]
Упрощенный обзор
В Эффект Яна – Теллера, иногда также называемый Искажение Яна – Теллера, описывает геометрическое искажение молекулы и ионы которые являются результатом определенных электронных конфигураций. В Теорема Яна – Теллера по существу утверждает, что любая нелинейная молекула с пространственно выродиться основное электронное состояние претерпевает геометрическое искажение, которое устраняет это вырождение, потому что искажение снижает общую энергию частиц. Описание другого типа геометрического искажения, возникающего в кристаллах с примесями замещения, см. В статье нецентральные ионы.
Химия переходных металлов

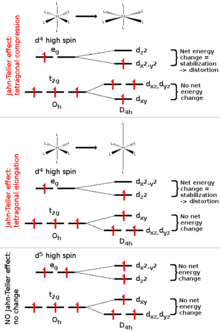
Эффект Яна – Теллера чаще всего встречается в октаэдрические комплексы переходных металлов.[3] Явление очень распространено в шести координатах медь (II) комплексы.[4] В d9 электронная конфигурация этого ион дает три электрона в двух вырожденных еграмм орбитали, приводящие к двукратно вырожденному электронному основному состоянию. Такие комплексы искажаются вдоль одной из осей четвертого порядка молекул (всегда обозначены z ось), что приводит к устранению орбитального и электронного вырождения и снижению общей энергии. Искажение обычно принимает форму удлинения связей с лигандами, лежащими вдоль z оси, но иногда вместо этого происходит сокращение этих связей (теорема Яна – Теллера не предсказывает направление искажения, только наличие нестабильной геометрии). Когда происходит такое удлинение, эффект заключается в снижении электростатического отталкивания между электронной парой на Льюис Бэйсик лиганд и любые электроны на орбиталях с z компонент, тем самым снижая энергию комплекса. Центр инверсии сохраняется после искажения.
В октаэдрических комплексах эффект Яна – Теллера наиболее выражен, когда нечетное число электронов занимает еграмм орбитали. Эта ситуация возникает в комплексе с конфигурациями d9, низкоскоростной d7 или же крутой d4 комплексы, все из которых имеют дважды вырожденные основные состояния. В таких соединениях еграмм орбитали, участвующие в вырождении, указывают непосредственно на лиганды, поэтому искажение может привести к большой энергетической стабилизации. Строго говоря, эффект возникает и при вырождении за счет электронов в т2 г орбитали (т.е. конфигурации, такие как d1 или же d2, оба из которых трехкратно вырождены). В таких случаях, однако, эффект гораздо менее заметен, потому что наблюдается гораздо меньшее снижение отталкивания при удалении лигандов от поверхности. т2 г орбитали, которые не указывают напрямую у лигандов (см. таблицу ниже). То же самое верно и в тетраэдрических комплексах (например, манганат: искажение очень тонкое, потому что требуется меньшая стабилизация, потому что лиганды не указывают прямо на орбитали.
Ожидаемые эффекты для октаэдрической координации приведены в следующей таблице:
| Количество d-электронов | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Высокий / Низкий спин | HS | LS | HS | LS | HS | LS | HS | LS | ||||||
| Сила J-T эффекта | ш | ш | s | ш | ш | ш | ш | s | s | |||||
w: слабый эффект Яна – Теллера (т2 г орбитали заняты неравномерно)
s: ожидается сильный эффект Яна – Теллера (еграмм орбитали заняты неравномерно)
пусто: эффекта Яна – Теллера не ожидается.
Эффект Яна – Теллера проявляется в УФ-ВИД спектры поглощения некоторых соединений, где это часто вызывает расщепление полос. Это хорошо видно в структуре многих комплексов меди (II).[5] Однако дополнительную подробную информацию об анизотропии таких комплексов и природе связывания лиганда можно получить из тонкой структуры низкотемпературного электронный спиновой резонанс спектры.

Связанные эффекты
Основная причина эффекта Яна – Теллера - наличие молекулярные орбитали это оба выродиться и открытая оболочка (т. е. не полностью заняты). Эта ситуация характерна не только для координационных комплексов, но и в других областях химии. В органической химии явление антиароматичность имеет ту же причину и часто видит искажение молекул; как в случае с циклобутадиен[6] и циклооктатетраен (СОТ).[7]
Расширенное лечение
Теорема Яна – Теллера.
Теорема JT может быть сформулирована в различных формах, две из которых приведены здесь:
- «Нелинейная многоатомная система в пространственно вырожденном электронном состоянии самопроизвольно искажается таким образом, что вырождение снимается и достигается новая равновесная структура более низкой симметрии».
Альтернативно и значительно короче:
- «... стабильность и вырождение невозможны одновременно, если молекула не является линейной ...».[8]
Спиновая дегенерация была исключением из первоначального лечения и позже рассматривалась отдельно.[9]
Формальное математическое доказательство теоремы Яна – Теллера в значительной степени опирается на аргументы симметрии, в частности на теории молекулярных точечные группы. Аргумент Ян и Кассир не предполагает никаких подробностей о электронная структура системы. Ян и Теллер не заявили о силе эффекта, который может быть настолько незначительным, что неизмеримо. Действительно, для электронов в несвязывающих или слабо связанных молекулярные орбитали, ожидается, что эффект будет слабым. Однако во многих ситуациях эффект JT важен.
Исторические события
Интерес к JTE возрос после его первой экспериментальной проверки. Были разработаны различные модельные системы, исследующие степень вырождение и тип симметрии.[10] Они были решены частично аналитически и частично численно, чтобы получить форму соответствующего поверхности потенциальной энергии (ППЭ) и уровни энергии для движения ядер на ППЭ с JT-расщеплением. Эти уровни энергии не колебательный уровни энергии в традиционном смысле из-за сложной связи с происходящим электронным движением, и их лучше назвать вибронный уровни энергии. Новое поле "вибронная муфта »Или« теория вибронной связи ».
Дальнейший прорыв произошел с появлением современных ("ab initio ") электронная структура расчеты, посредством которых соответствующие параметры, характеризующие системы JT, могут быть надежно определены из первых принципов. Таким образом, можно выйти за рамки исследований модельных систем, которые исследуют влияние вариаций параметров на PES и вибронный уровни энергии; можно было бы выйти за рамки подгонки этих параметров к экспериментальным данным, не зная четкого значения подгонки. Вместо этого стали возможны хорошо обоснованные теоретические исследования, которые значительно улучшили понимание рассматриваемых явлений и деталей лежащих в основе механизмов.

Признавая искажение JTE как конкретный пример общего спонтанное нарушение симметрии механизма, точное вырождение вовлеченного электронного состояния было идентифицировано как несущественный ингредиент для этого нарушение симметрии в многоатомных системах. Даже системы, которые в неискаженной симметричной конфигурации представляют электронные состояния, близкие по энергии, но не точно вырожденные, могут проявлять аналогичную тенденцию к искажению. Искажения этих систем можно рассматривать в рамках связанной теории псевдо эффект Яна – Теллера (в литературе часто именуется «JTE второго порядка»). Этот механизм связан с вибронными связями между адиабатическими ППЭ, разделенными ненулевыми энергетическими зазорами в конфигурационном пространстве: его включение расширяет применимость связанных с ЯТ моделей к нарушению симметрии в гораздо более широком диапазоне молекулярных и твердотельных систем.
Хронология:
- 1934: Лев Ландау, обсуждая с Эдвард Теллер, предположил, что электронные состояния некоторых вырожденных ядерных конфигураций нестабильны по отношению к ядерным смещениям, которые понижают симметрию (см. «Историческую заметку» Энглмана [11]).
- 1937: Герман Артур Ян и Эдвард Теллер сформулировал то, что теперь известно как теорема Яна – Теллера.[8]
- 1939: Джон Хасбрук Ван Флек распространил теорему Яна – Теллера на ионы в кристаллах. Поскольку попытки наблюдать эффект Яна – Теллера экспериментально были неубедительными, он отметил, что «большое достоинство эффекта Яна – Теллера заключается в том, что он исчезает, когда в нем нет необходимости».[12][13]
- 1950-2: Brebis Bleaney и сотрудники впервые получили недвусмысленное экспериментальное доказательство эффекта Яна – Теллера, выполнив электронный парамагнитный резонанс исследования парамагнитных ионов в кристаллах [14][15]
- 1957-8: Эпик и Прайс показали, что спин-орбитальная связь может стабилизировать симметричные конфигурации от искажений из-за слабого JTE.[16] Moffitt et al.[17][18] и Longuet-Higgins et al.[19] утверждали, что состояния JT-систем имеют неразрывно смешанные электронные и колебательные компоненты, которые они назвали вибронный состояния, энергия которых сильно отличается от электронных состояний.
- 1962-4: Исаак Берсукер [20] и Мэри О’Брайен [21] исследовали туннелирование в низкоэнергетических вибронный состояний, так называемого туннельного расщепления и динамической природы ЯТ-эффекта. В статье О'Брайена показано влияние геометрического фазового фактора (позже названного фазой Берри) на упорядочение вибронных состояний.
- 1965: Фрэнк Хэм осознал влияние когерентной динамики на измерение наблюдаемых. Это влияние можно описать с помощью понижающих коэффициентов, умножающих орбитальные операторы. [22] предложены конкретные формулы для магнетизма ионов ЯТ.
- 1984: Обобщение концепции геометрическая фаза к ягода[23] (или фаза Берри, как ее также называют) обеспечила общий фон, чтобы помочь понять фазу, зависящую от вращения, связанную с электронной и колебательной волновой функцией JT-систем, как обнаружил Лонге-Хиггинс,[19] и далее обсуждались Герцбергом и Лонге-Хиггинсом,[24] Лонге-Хиггинс,[25] О'Брайен,[21] и Мид и Трухлар.[26]
- 1990-е годы: достижения в области вычислительной мощности означали, что ab initio методы, в том числе основанные на Функциональная теория плотности начали использоваться для решения проблем JT.
Отношение к важным открытиям
- В 1985 г. Гарри Крото и сотрудники открыли класс молекул углерода с замкнутой клеткой, известный как фуллерены.[27] Бакминстерфуллерен (C60), у которого есть икосаэдрическая симметрия, становится JT-активным при добавлении или удалении одного электрона.[28] Порядок уровней энергии может отличаться от того, который предсказал Правило Хунда.
- Открытие в 1986 году Беднорцем и Мюллер из сверхпроводимость в купратах с температурой перехода 35 К,[29] который был выше верхнего предела, разрешенного согласно стандартной теории БКШ, был мотивирован более ранней работой Мюллера по ионам JT в кристаллах.
- Колоссальное магнитосопротивление, собственность марганец -основан перовскиты и других материалов, было объяснено с точки зрения конкуренции между динамическими эффектами Яна – Теллера и двойным обменом.[30]
- Теорема Пайерлса, который утверждает, что одномерная равноотстоящая цепочка ионов с одним электроном на ион нестабильна, имеет общие корни с эффектом JT.
Теория
Симметрия JT-систем и категоризация с использованием теории групп
У данной проблемы JT будет определенная точечная групповая симметрия, Такие как Тd симметрия для магнитных примесных ионов в полупроводники или же ячас симметрия для фуллерен C60. Проблемы JT обычно классифицируются с использованием меток для неприводимые представления (Reps), которые относятся к симметрии электронного и колебательного состояний. Например, E ⊗ e будет относиться к состоянию электронного дублета, преобразующемуся как E, связанному с преобразованием состояния колебательного дублета как e.
В общем, колебательная мода, преобразующаяся как Λ, будет соединяться с электронным состоянием, трансформирующимся как Γ, если симметричная часть Кронекер продукт [Γ ⊗ Γ]S содержит Λ, если Γ не является двойная группа представление, когда антисимметричная часть {Γ ⊗ Γ}А рассматривается вместо этого. Режимы, которые делают пару, считаются JT-активными.
В качестве примера рассмотрим дублетное электронное состояние E с кубической симметрией. Симметричная часть E ⊗ E - это A1 + E. Следовательно, состояние E будет соединяться с колебательными модами трансформируется как1 и е. Однако1 моды приведут к одинаковому сдвигу энергии для всех состояний и, следовательно, не будут способствовать какому-либо JT-расщеплению. Поэтому ими можно пренебречь. Результат - эффект E ⊗ e JT. Этот эффект JT испытывают треугольные молекулы X3, тетраэдрические молекулы ML4, и октаэдрические молекулы ML6 когда их электронное состояние имеет E-симметрию.
Компоненты данной колебательной моды также маркируются в соответствии с их свойствами преобразования. Например, два компонента режима e обычно обозначаются и , который в октаэдрическая симметрия преобразовать как и соответственно.
Гамильтониан JT
Собственные значения Гамильтониан многоатомной системы определяют ПЭС как функции нормальных режимов системы (т.е. линейные комбинации ядерных смещений с определенными свойствами симметрии). В реперной точке высокой симметрии, где возникает вырождение, индуцированное симметрией, несколько собственных значений совпадают. Путем подробного и кропотливого анализа Ян и Кассир показал, что - за исключением линейных молекул - всегда есть члены первого порядка в разложении матричных элементов гамильтониана по понижающим симметрию (на языке теория групп: неполностью симметричный) нормальные моды. Эти линейные члены представляют силы, которые искажают систему по этим координатам и снимают вырождение. Таким образом, точка вырождения не может быть стационарной, и система искажается в направлении стационарной точки более низкой симметрии, где может быть достигнута стабильность.
Доказательство теоремы JT следует из теории симметрии молекул (точечная группа теория). Менее строгое, но более интуитивное объяснение дается в разделе .
Чтобы получить количественное описание эффекта ЯТ, силы, возникающие между компонентами волновые функции описываются разложением гамильтониана в ряд по степеням . В силу самой природы вырождения гамильтониан принимает форму матрицы, относящейся к вырожденному волновая функция составные части. А матричный элемент между штатами и обычно читается как:
Разложение можно усечь после членов, линейных по , или расширен, чтобы включить термины, квадратичные (или более высокие) в .
В адиабатический поверхности потенциальной энергии (APES) тогда получаются как собственные значения этой матрицы. В оригинальной статье доказано, что в разложении всегда есть линейные члены. Отсюда следует, что вырождение волновая функция не может соответствовать стабильной конструкции.
Поверхности потенциальной энергии
Потенциал мексиканской шляпы
С математической точки зрения, APES, характеризующие искажение JT, возникают как собственные значения матрицы потенциальной энергии. Как правило, APES имеют характерный вид двойного конуса, круглого или эллиптического, где точка контакта, то есть вырождение, обозначает конфигурацию с высокой симметрией, для которой применима теорема JT. Для указанного выше случая линейного E E e JT-эффекта ситуация иллюстрируется APES
изображенный на рисунке, с вырезанной частью, чтобы показать его форму, которая известна как потенциал мексиканской шляпы. Здесь, - частота колебательной е-моды, это его масса и является мерой прочности соединения JT.

Коническая форма вблизи вырождения в начале координат сразу дает понять, что эту точку нельзя стационарный, то есть система неустойчива по отношению к асимметричным искажениям, что приводит к понижению симметрии. В этом частном случае изоэнергетических искажений ЯТ бесконечно много. В дающие эти искажения расположены по кругу, как показано красной кривой на рисунке. Квадратичная связь или кубические упругие члены приводят к искривлению вдоль этого «пути минимальной энергии», заменяя это бесконечное многообразие тремя эквивалентными минимумами потенциала и тремя эквивалентными седловыми точками. В других системах JT линейная связь приводит к дискретным минимумам.
Конические пересечения
Высокая симметрия топологии двойного конуса линейной системы E ⊗ e JT напрямую отражает высокую симметрию, лежащую в основе. Это один из самых ранних (если не самый ранний) примеров в литературе коническое пересечение поверхностей потенциальной энергии. Конические пересечения получили широкое внимание в литературе, начиная с 1990-х годов, и теперь считаются парадигмами неадиабатической динамики возбужденного состояния, что имеет далеко идущие последствия в молекулярной спектроскопии. фотохимия и фотофизика. Некоторые из них будут прокомментированы ниже. В целом, конические пересечения гораздо менее симметричны, чем изображено на рисунке. Они могут быть наклонными, эллиптическими по форме и т. Д., А также в литературе выделяются остроконечные и наклонные пересечения. Кроме того, для более чем двух степеней свободы они не являются точечными структурами, а представляют собой швы и сложные изогнутые гиперповерхности, также известные как пространство пересечений. Подпространство координат, показанное на рисунке, также известно как плоскость ветвления.
Последствия для динамики
Характерная форма JT-расщепленных APES имеет определенные последствия для ядерной динамики, рассматриваемой здесь в полностью квантовом смысле. При достаточно сильной JT-связи точки минимума находятся достаточно далеко (по крайней мере, на несколько квантов колебательной энергии) ниже JT-пересечения. Таким образом, следует различать два различных энергетических режима: низкоэнергетический и высокоэнергетический.
- В низкоэнергетическом режиме движение ядра ограничено областями вблизи «точек минимума энергии». Отобранные искаженные конфигурации передают свои геометрические параметры, например, вращательной тонкой структуре в спектре. Из-за существования барьеров между различными минимумами в APES, подобных тем, которые возникают из-за деформации , движение в низкоэнергетическом режиме обычно классифицируется как статический JTE, динамический JTE или некогерентный прыжок. Каждый режим показывает определенные отпечатки пальцев при экспериментальных измерениях.
- Статический JTE: В этом случае система оказывается в ловушке в одном из минимумов с наименьшей энергией APES (обычно определяется небольшими возмущениями, создаваемыми окружающей средой JT-системы) и не имеет достаточной энергии, чтобы пересечь барьер к другому минимуму во время типичное время, связанное с измерением. Квантовыми динамическими эффектами, такими как туннелирование, можно пренебречь, и молекула или твердое тело эффективно демонстрируют низкую симметрию, связанную с одним минимумом.
- Динамический JTE:[31] В этом случае, барьеры достаточно малы по сравнению с, например, энергией нулевой точки, связанная с минимумами, так что колебательные волновые функции (и все наблюдаемые) отобразить симметрию ссылки (искаженной) систему. В линейной задаче E ⊗ e движение, связанное с этим режимом, будет происходить по круговой траектории на рисунке. Когда барьер достаточно мал, это называется (свободным) псевдовращением (не путать с вращением твердого тела в пространстве, см. Проиллюстрированную разницу между реальным и псевдовращением. здесь для молекула фуллерена C60). Когда барьер между минимумами и седловыми точками на искривленном пути превышает вибрационный квант, псевдовращательное движение замедляется и происходит за счет туннелирования. Это называется затрудненным псевдовращением. Как при свободном, так и при затрудненном псевдовращении важное явление геометрической (Берри) фазы изменяет порядок уровней.
- Некогерентный скачок: Еще один способ преодоления барьера - получение тепловой энергии. В этом случае, пока система движется по минимумам системы, состояние не является квантово-когерентным, а является статистической смесью. Это различие можно наблюдать экспериментально.
- Динамика совершенно иная для высоких энергий, например, при оптическом переходе из невырожденного начального состояния с высокосимметричной (неискаженной JT) геометрией равновесия в искаженное состояние JT. Это приводит систему к области около конического пересечения JT-расщепленных APES в центре рисунка. Здесь неадиабатические связи становятся очень большими, и поведение системы не может быть описано в рамках знакомого Борн-Оппенгеймер (BO) разделение электронного и ядерного движения. Ядерное движение перестает ограничиваться одним четко определенным APES, и переходы между адиабатическими поверхностями происходят, приводя к эффектам, подобным резонансам Слонжевского. В молекулах это обычно фемтосекундная шкала времени, что соответствует сверхбыстрым (фемтосекундным) процессам внутреннего преобразования, сопровождающимся широкими спектральными полосами также в условиях изолированной молекулы и очень сложными спектральными характеристиками. Примеры этих явлений будут рассмотрены в разделе .
Как уже указывалось выше, различие режимов низкой и высокой энергии справедливо только для достаточно сильных JT-взаимодействий, то есть когда несколько или много квантов колебательной энергии помещаются в энергетическое окно между коническим пересечением и минимумом нижнего JT-расщепления. ОБЕЗЬЯНЫ. Для многих случаев малых и промежуточных JT-взаимодействий это энергетическое окно и соответствующий адиабатический низкоэнергетический режим не существует. Скорее, уровни на обоих JT-расщепленных APES замысловато перемешаны для всех энергий, и ядерное движение всегда происходит на обоих JT-расщепленных APES одновременно.
Факторы ветчины
В 1965 году Фрэнк Хэм [22] предположил, что динамический JTE может уменьшить ожидаемые значения наблюдаемых, связанных с орбитальными волновыми функциями из-за суперпозиции нескольких электронных состояний в полной вибронной волновой функции. Этот эффект приводит, например, к частичному тушению спин-орбитального взаимодействия[22][32] и позволил результаты предыдущих Электронный парамагнитный резонанс (ЭПР) эксперименты, требующие пояснения.
В общем случае результат орбитального оператора, действующего на вибронные состояния, может быть заменен эффективным орбитальным оператором, действующим на чисто электронные состояния.В первом порядке эффективный орбитальный оператор равен фактическому орбитальному оператору, умноженному на константу, значение которой меньше единицы, известное как понижающий коэффициент первого порядка (Ham). Например, в тройке T1 электронное состояние, оператор спин-орбитальной связи можно заменить на , куда является функцией силы JT-связи, которая изменяется от 1 при нулевой связи до 0 при очень сильной связи. Кроме того, когда включаются поправки на возмущение второго порядка, вводятся дополнительные члены, включающие дополнительные числовые коэффициенты, известные как понижающие коэффициенты второго порядка (Ham). Эти факторы равны нулю, когда нет JT-связи, но могут преобладать над членами первого порядка при сильной связи, когда эффекты первого порядка значительно уменьшены.[10]
Коэффициенты уменьшения особенно полезны для описания экспериментальных результатов, таких как EPR и оптические спектры парамагнитный примеси в полупроводник, диэлектрик, диамагнитный и ферримагнитный хосты.
Современные разработки
В течение долгого времени приложения теории JT заключались в основном в исследованиях параметров (исследования моделей), где APES и динамические свойства JT-систем изучались как функции от параметров системы, таких как константы связи и т. Д. Соответствие этих параметров экспериментальным данным было часто сомнительный и безрезультатный. Ситуация изменилась в 1980-х годах, когда были разработаны эффективные ab initio методы, а вычислительные ресурсы стали достаточно мощными, чтобы обеспечить надежное определение этих параметров из первых принципов.[33] Помимо волновая функция -основанные методы (которые иногда считаются подлинно ab initio в литературе) появление теория функционала плотности (DFT) открыла новые возможности для обработки более крупных систем, включая твердые тела. Это позволило охарактеризовать детали систем JT и надежно интерпретировать экспериментальные данные. Он лежит в основе большинства разработок, рассматриваемых в разделе .
Возможны две разные стратегии, которые использовались в литературе. Можно
- считать применимость определенной схемы связи само собой разумеющимся и ограничиться определением параметров модели, например, исходя из выигрыша в энергии, достигнутого за счет искажения JT, также называемого энергией стабилизации JT.
- отображать части APES в целом или в уменьшенной размерности и, таким образом, получить представление о применимости модели, возможно, также получить идеи о том, как ее расширить.
Естественно, более точный подход (2) может быть ограничен меньшими системами, в то время как более простой подход (1) поддается изучению более крупных систем.
Приложения
Воздействие на структуру
Маленькие молекулы и ионы
JT-искажение малых молекул (или молекулярных ионов) непосредственно выводится из расчетов электронной структуры их APES (через DFT и / или вычисления ab initio). Эти молекулы / ионы часто являются радикалами, такими как тримеры щелочных атомов (Li3 и Na3), которые имеют неспаренные спины и, в частности, находятся (но не ограничиваются ими) в дублетных состояниях. Помимо JTE в 2E 'и 2E », а также между состоянием E и ближайшим состоянием A может играть роль. JT-искажение снижает симметрию от D3ч в C2v (см. рисунок), и от деталей взаимодействий зависит, имеет ли равнобедренный треугольник острый или тупой угол (например, Na3) минимальная энергетическая структура. Естественные расширения - это такие системы, как NO3 и NH3+ где в литературе описано JT-искажение для основного или возбужденного электронных состояний.

Несколько особую роль играют тетраэдрические системы типа CH4+ и P4+. Здесь играют роль трехкратно вырожденные электронные состояния и колебательные моды. Тем не менее, двойное вырождение продолжает иметь значение.
Среди более крупных систем в литературе основное внимание уделяется бензолу и его катион-радикалам, а также их галогенпроизводным (особенно фтор). Уже в начале 80-х годов прошлого века из детального анализа экспериментальных спектров излучения катион-радикалов 1,3,5-трифтор- и гексафтор (и хлор) бензола был получен большой объем информации. Эффект Яна-Теллера в катионе-радикале 1,3,5-трифторбензола обсуждается в разделе 13.4.2 учебника Банкера и Йенсена.[1] Для родительского катиона бензола следует полагаться на фотоэлектронные спектры со сравнительно более низким разрешением, поскольку этот вид не флуоресцирует (см. Также раздел о ). Были выполнены довольно подробные расчеты ab initio, которые документируют энергии стабилизации JT для различных (четырех) активных мод JT, а также количественно определяют умеренные барьеры для псевдовращения JT.
Наконец, несколько особую роль играют системы с осью симметрии пятого порядка, подобные циклопентадиенильному радикалу. Тщательные лазерные спектроскопические исследования пролили свет на ЯТ-взаимодействия. В частности, они показывают, что барьер для псевдовращения почти исчезает (система сильно «текучая»), что можно объяснить тем фактом, что члены связи 2-го порядка исчезают по симметрии, а главные члены более высокого порядка имеют 4-й порядок.
Координационная химия
JTE обычно сильнее там, где электронная плотность, связанная с вырожденными орбиталями, более сконцентрирована. Таким образом, этот эффект играет большую роль в определении структуры комплексов переходных металлов с активными внутренними 3d-орбиталями.


Наиболее знаковой и заметной из систем JT в координационной химии, вероятно, являются октаэдрические комплексы Cu (II). Хотя в совершенно эквивалентной координации, как CuF6 комплекс, связанный с примесью Cu (II) в кубическом кристалле типа KMgF3, совершенный октаэдр (Oчас) симметрия ожидается. Фактически, более низкая тетрагональная симметрия обычно обнаруживается экспериментально. Происхождение этого искажения JTE было выяснено путем изучения электронной конфигурации неискаженного комплекса. Для октаэдрической геометрии пять трехмерных орбиталей разбиваются на t2 г и еграмм орбитали (см. диаграмму). Эти орбитали заняты девятью электронами, соответствующими электронная конфигурация Cu (II). Таким образом, t2 г оболочка заполнена, а буква еграмм оболочка содержит 3 электрона. В целом неспаренный электрон производит 2Eграмм состояние, которое является активным по Ян-Теллеру. Третий электрон может занимать любую из орбиталей, составляющих eграмм оболочка: в основном орбитальный или в основном орбитальный. Если электрон занимает в основном Уровень, на котором разрыхляющая орбиталь окончательная геометрия комплекса будет удлинена, так как аксиальные лиганды будут отталкиваться, чтобы уменьшить общую энергию системы. С другой стороны, если электрон попадет в основной орбитальный антибонд, комплекс исказил бы в сжатую геометрию. Экспериментально вытянутые геометрические формы наблюдаются в подавляющем большинстве случаев, и этот факт приписывают как ангармоническим взаимодействиям металл-лиганд. [16] и гибридизации 3d-4s.[34] Учитывая, что все направления, содержащие ось четвертого порядка, эквивалентны, искажение с одинаковой вероятностью произойдет в любой из этих ориентаций. С электронной точки зрения это означает, что и орбитали, которые вырождены и могут гибридизоваться в октаэдрической геометрии, будут смешиваться, чтобы произвести соответствующие эквивалентные орбитали в каждом направлении, например или же .
JTE не ограничивается только октаэдрическими комплексами Cu (II). Есть много других конфигураций, включающих изменения как исходной структуры, так и электронной конфигурации металла, которые приводят к вырожденным состояниям и, таким образом, JTE. Однако величина искажения и энергия стабилизации эффекта сильно зависит от конкретного случая. В октаэдрической Cu (II) JTE особенно сильно, потому что
- вырожденные орбитали демонстрируют сильно разрыхляющий σ-характер
- Cu - переходный металл с относительно прочным электроотрицательность дает больше ковалентных связей, чем другие металлы, что позволяет увеличить константу линейной связи JT.
В других конфигурациях, включающих π- или δ-связывание, например, когда вырожденное состояние связано с t2 г орбиталей октаэдрической конфигурации, энергии искажения и стабилизации обычно намного меньше, и возможность не наблюдать искажение из-за динамических эффектов JT намного выше. Точно так же для редкоземельных ионов, где ковалентность очень мала, искажения, связанные с JTE, обычно очень слабые.
Важно отметить, что JTE ассоциируется со строгим вырождением в электронной подсистеме и поэтому не может появиться в системах без этого свойства. Например, JTE часто ассоциируется с квазиоктаэдрическими CuX2Y4 комплексы, где расстояния до X и Y лиганды явно разные. Однако внутренняя симметрия этих комплексов уже тетрагональна и не имеет вырожденных eграмм орбиталь существует, разделившись на1 г (в основном ) и b1 г (в основном ) орбитали из-за различных электронных взаимодействий с осевым X лиганды и экваториальный Y лиганды. В этом и других подобных случаях некоторые оставшиеся вибронные эффекты, связанные с JTE, все еще присутствуют, но гасятся по сравнению со случаем вырождения из-за расщепления орбиталей.
Спектроскопия и реакционная способность
Из спектров с вращательным разрешением моменты инерции и, следовательно, длины связей и углы могут быть определены «напрямую» (по крайней мере, в принципе). Из менее хорошо разрешенных спектров все же можно определить важные величины, такие как энергии стабилизации JT и энергетические барьеры (например, для псевдовращения). Однако во всем спектральном распределении интенсивности электронного перехода закодировано больше информации. Он использовался для принятия решения о наличии (или отсутствии) геометрической фазы, которая накапливается во время псевдовращательного движения вокруг JT (или другого типа) конического пересечения. Яркими примерами любого типа являются основное (X) или возбужденное (B) состояние Na3. Преобразование Фурье , так называемая автокорреляционная функция отражает движение волнового пакета после оптического (= вертикального) перехода к APES конечного электронного состояния. Обычно он перемещается по временной шкале периода колебаний, который (для небольших молекул) составляет порядка 5-50 фс, то есть сверхбыстрый. Помимо почти периодического движения, могут также возникать модовые взаимодействия с очень нерегулярным (также хаотическим) поведением и расширением волнового пакета. Вблизи конического пересечения это будет сопровождаться / дополняться безызлучательными переходами (так называемая внутренняя конверсия) в другие APES, происходящие в том же сверхбыстром временном масштабе.
Для случая JT ситуация несколько особенная по сравнению с общим коническим пересечением, потому что различные потенциальные слои JT симметрично связаны друг с другом и имеют (точно или почти) тот же минимум энергии. Таким образом, «переход» между ними более колебательный, чем можно было бы ожидать, а их усредненная по времени популяция близка к 1/2. Для более типичного сценария «требуется» более общее коническое пересечение.
Эффект ЯТ по-прежнему играет роль, а именно в сочетании с другим близким, в общем невырожденным электронным состоянием. В результате псевдо эффект Яна – Теллера, например, состояния E, взаимодействующего с состоянием A. Эта ситуация обычна для JT-систем, так же как взаимодействия между двумя невырожденными электронными состояниями являются обычными для не-JT-систем. Примеры - возбужденные электронные состояния NH3+ и катион-радикал бензола. Здесь пересечения APES в состояниях E и A представляют собой тройные пересечения, которые связаны с очень сложными спектральными характеристиками (плотные линейные структуры и диффузные спектральные огибающие при низком разрешении). Перенос населения между состояниями также сверхбыстрый, настолько быстрый, что флуоресценция (протекающая в наносекундном масштабе времени) не может конкурировать. Это помогает понять, почему катион бензола, как и многие другие катион-радикалы органических соединений, не флуоресцирует.
Безусловно, фотохимическая реакционная способность возникает, когда внутреннее преобразование заставляет систему исследовать пространство ядерной конфигурации, так что образуются новые химические частицы. Существует множество методов фемтосекундной спектроскопии с накачкой и зондом, позволяющих выявить детали этих процессов, происходящих, например, в процессе зрения.
Проблемы с твердым телом
По первоначальному предложению Ландау [35]свободные электроны в твердом теле, введенные, например, путем легирования или облучения, могут взаимодействовать с колебаниями решетки с образованием локализованной квазичастицы, известной как полярон. Сильно локализованные поляроны (также называемые поляронами Холстейна) могут конденсироваться вокруг высокосимметричных узлов решетки с электронами или дырками, занимающими локальные вырожденные орбитали, которые испытывают JTE. Эти поляроны Яна-Теллера нарушают как трансляционную, так и точечную симметрию группы решетки, в которой они находятся, и им приписывают важную роль в таких эффектах, как колоссальное магнитосопротивление и сверхпроводимость.
Парамагнитный примеси в полупроводник, диэлектрик, диамагнитный и ферримагнитный все хосты можно описать с помощью модели JT. Например, эти модели широко использовались в 1980-х и 1990-х годах для описания ионов Cr, V и Ti, замещающих Ga в GaAs и GaP.
В фуллерен C60 может образовывать твердые соединения с щелочными металлами, известными как фуллериды. CS3C60 может быть сверхпроводящим при температурах до 38K под приложенным давлением,[36] тогда как соединения формы A4C60 являются изоляционными (по мнению Гуннарссона [37]). JT эффекты как в пределах C60 молекулы (внутримолекулярные) и между C60 Молекулы (межмолекулярные) играют роль в механизмах, лежащих в основе различных наблюдаемых свойств в этих системах. Например, они могут означать, что Трактовка Мигдала-Элиашберга сверхпроводимости ломается. Кроме того, фуллериды могут образовывать так называемое новое состояние вещества, известное как металл Яна-Теллера, где локализованные электроны сосуществуют с металличность и JT искажения на C60 молекулы сохраняются [38]
Кооперативный эффект JT в кристаллах
JTE обычно ассоциируется с вырождением, которое хорошо локализовано в пространстве, например, с вырождением в небольшой молекуле или с изолированным комплексом переходного металла. Однако во многих периодических высокосимметричных твердотельных системах, таких как перовскиты, некоторые кристаллические узлы допускают электронное вырождение, приводящее при адекватном составе к решеткам JT-активных центров. Это может привести к кооперативному JTE, в котором глобальные искажения кристалла происходят из-за локальных вырождений.
Чтобы определить окончательную электронную и геометрическую структуру кооперативной JT-системы, необходимо учитывать как локальные искажения, так и взаимодействие между различными узлами, которые будут принимать такую форму, которая необходима для минимизации глобальной энергии кристалла.
Пока работы над кооперативом JTE начались в конце пятидесятых годов. [39],[40] это было в 1960 году, когда Канамори [41] опубликовал первую работу по кооперативному JTE, в которой были введены многие важные элементы современной теории этого эффекта. Это включало использование обозначения псевдоспина для обсуждения орбитального упорядочения и обсуждение важности JTE для обсуждения магнетизма, конкуренции этого эффекта со спин-орбитальной связью и связи искажений с деформацией решетки. Этот момент был позже подчеркнут в обзоре Геринга и Геринга. [42] как ключевой элемент для установления дальнего порядка между искажениями в решетке. Важная часть современной теории кооперативного JTE,[43] может привести к структурным фазовые переходы.
Важно отметить, что многие кооперативные системы JT, как ожидается, будут металлами из зонной теории, так как для их создания вырожденная орбиталь должна быть частично заполнена, а связанная с ней зона будет металлической. Однако под воздействием искажения нарушения симметрии, связанного с кооперативным JTE, вырождения в электронной структуре разрушаются, и основное состояние этих систем часто оказывается изолирующим (см., Например,[44]). Во многих важных случаях, таких как исходное соединение для колоссальное магнитосопротивление перовскиты, LaMnO3, повышение температуры приводит к беспорядку в искажениях, что снижает расщепление зон из-за кооперативного JTE, тем самым вызывая переход металл-изолятор.
В современной физике твердого тела принято классифицировать системы в соответствии с имеющимися у них степенями свободы, например электрон (металлы) или спин (магнетизм). В кристаллах, которые могут отображать JTE, и до того, как этот эффект будет реализован посредством искажений, нарушающих симметрию, обнаружено, что существует орбитальная степень свободы, состоящая в том, как электроны занимают локальные вырожденные орбитали. Как первоначально обсуждали Кугель и Хомский,[45] не все конфигурации эквивалентны. Ключевым моментом является относительная ориентация этих занятых орбиталей, так же как ориентация спина важна в магнитных системах, а основное состояние может быть реализовано только для некоторой конкретной орбитальной схемы. И этот паттерн, и эффект, вызывающий это явление, обычно называют орбитальным упорядочением.
Чтобы предсказать паттерн орбитального упорядочения, Кугель и Хомский использовали конкретизацию Модель Хаббарда. В частности, они установили, как суперобмен взаимодействия, обычно описываемые правилами Андерсона – Канамори – Гуденафа, изменяются при наличии вырожденных орбиталей. Их модель, использующая представление псевдоспина для локальных орбиталей, приводит к Гейзенберг-подобная модель в котором основное состояние представляет собой комбинацию орбитальных и спиновых паттернов. Используя эту модель, можно показать, например, что происхождение необычной изоляции заземления ферромагнитный состояние твердого тела типа K2CuF4 можно проследить его орбитальное упорядочение.
Даже если исходить из относительно высокосимметричной структуры, комбинированный эффект обменных взаимодействий, спин-орбитального взаимодействия, орбитального упорядочения и деформаций кристаллов, активируемых JTE, может привести к магнитным структурам очень низкой симметрии с определенными свойствами. Например, в CsCuCl3 появляется несоизмеримая геликоидальная картина как для орбиталей, так и для искажений вдоль -ось. Более того, многие из этих соединений демонстрируют сложные фазовые диаграммы при изменении температуры или давления.
Рекомендации
- ^ а б Бункер, Филип Р .; Дженсен, Пер (1998) Молекулярная симметрия и спектроскопия (2-е изд.). NRC Research Press, Оттава [1]ISBN 9780660196282
- ^ Перссон, Ингмар (2010). «Гидратированные ионы металлов в водном растворе: насколько регулярны их структуры?». Чистая и прикладная химия. 82 (10): 1901–1917. Дои:10.1351 / PAC-CON-09-10-22.
- ^ Шрайвер, Д. Ф .; Аткинс, П. В. (1999). Неорганическая химия (3-е изд.). Издательство Оксфордского университета. С. 235–236. ISBN 978-0-19-850330-9.
- ^ Джейнс, Роб; Мур, Элейн А. (2004). Связывание металл-лиганд. Королевское химическое общество. ISBN 978-0-85404-979-0.
- ^ Фрэнк, Патрик; Бенфатто, Маурицио; Szilagyi, Роберт К .; Д'Анджело, Паола; Делла Лонга, Стефано; Ходжсон, Кейт О. (2005). "Структура раствора [Cu (водн.)]2+ и его значение для индуцированного стойкой связывания в активных сайтах с синим медным белком ». Неорганическая химия. 44 (6): 1922–1933. Дои:10.1021 / ic0400639. PMID 15762718.
- ^ Сенн, Питер (октябрь 1992 г.). «Простая квантово-механическая модель, иллюстрирующая эффект Яна – Теллера». Журнал химического образования. 69 (10): 819. Bibcode:1992JChEd..69..819S. Дои:10.1021 / ed069p819.
- ^ Кларнер, Франк-Геррит (2001). «Об антиароматичности планарного циклооктатетраена». Angewandte Chemie International Edition на английском языке. 40 (21): 3977–3981. Дои:10.1002 / 1521-3773 (20011105) 40:21 <3977 :: AID-ANIE3977> 3.0.CO; 2-N.
- ^ а б Jahn, H.A .; Теллер, Э. (1937). «Стабильность многоатомных молекул в вырожденных электронных состояниях. I. Орбитальное вырождение». Proc. R. Soc. А. 161 (A905): 220–235. Bibcode:1937RSPSA.161..220J. Дои:10.1098 / rspa.1937.0142.
- ^ Берсукер, И. Б. (2006). Эффект Яна – Теллера. Кембридж: Издательство Кембриджского университета. ISBN 9780521822121.
- ^ а б Бейтс, К. А. (1978). «Эффекты Яна – Теллера в парамагнитных кристаллах». Отчеты по физике. 35 (3): 187–304. Bibcode:1978ФР .... 35..187Б. Дои:10.1016/0370-1573(78)90122-9.
- ^ Энглман Р. (1972). Эффект Яна – Теллера в молекулах и кристаллах.. Wiley-Interscience. ISBN 9780471241683.
- ^ Ван Флек, Дж. Х. (1939). «О магнитном поведении ванадия, титана и хромовых квасцов». J. Chem. Phys. 7 (1): 61–71. Bibcode:1939ЖЧФ ... 7 ... 61В. Дои:10.1063/1.1750326.
- ^ Ван Флек, Дж. Х. (1939). «Эффект Яна – Теллера и кристаллическое штарковое расщепление для кластеров вида XY6». J. Chem. Phys. 7 (1): 72–84. Bibcode:1939ЖЧФ ... 7 ... 72В. Дои:10.1063/1.1750327.
- ^ Bleaney, B .; Инграм, Д. Дж. Э. (1950). «Парамагнитный резонанс во фторосиликате меди». Proc. R. Soc. А. 63 (364): 408–409. Bibcode:1950PPSA ... 63..408B. Дои:10.1088/0370-1298/63/4/112.
- ^ Bleaney, B .; Бауэрс, К. Д. (1952). «Ион меди в тригонально-кристаллическом электрическом поле». Proc. R. Soc. А. 65 (392): 667–668. Bibcode:1952PPSA ... 65..667B. Дои:10.1088/0370-1298/65/8/111.
- ^ а б Öpik, U .; Прайс, М. Х. Л. (1957). "Исследования эффекта Яна Теллера. 1. Обзор статической проблемы". Proc. R. Soc. А. 238 (1215): 425–447. Bibcode:1957RSPSA.238..425O. Дои:10.1098 / RSPA.1957.0010.
- ^ Moffitt, W .; Торсон, В. (1957). «Вибронные состояния октаэдрических комплексов». Физический обзор. 108 (5): 1251–1255. Bibcode:1957ПхРв..108.1251М. Дои:10.1103 / PhysRev.108.1251.
- ^ Moffitt, W .; Лир, А. Д. (1957). «Конфигурационная неустойчивость вырожденных электронных состояний». Физический обзор. 106 (6): 1195–1200. Bibcode:1957ПхРв..106.1195М. Дои:10.1103 / PhysRev.106.1195.
- ^ а б Longuet-Higgins, H.C .; Öpik, U .; Pryce, M.H.L .; Сак, Р. А. (1958). «Исследования эффекта Яна – Теллера. 2. Динамическая проблема». Proc. R. Soc. А. 244 (1236): 1–16. Bibcode:1958RSPSA.244 .... 1л. Дои:10.1098 / rspa.1958.0022.
- ^ Берсукер, И. Б. (1963). «Инверсионное расщепление уровней в свободных комплексах переходных металлов». Сов. Phys. ЖЭТФ. 16 (4): 933–938. Bibcode:1963JETP ... 16..933B.
- ^ а б О'Брайен, М.С.М. (1964). "Динамический эффект Яна – Теллера в октаэдрически согласованных d9 Ионы ». Proc. R. Soc. А. 281 (1384): 323–339. Bibcode:1964RSPSA.281..323O. Дои:10.1098 / rspa.1964.0185.
- ^ а б c Хэм, Ф. С. (1965). «Динамический эффект Яна – Теллера в спектрах парамагнитного резонанса - орбитальные коэффициенты редукции и частичное тушение спин-орбитального взаимодействия». Физический обзор. 138 (6A): A1727 – A1740. Bibcode:1965ПхРв..138.1727Г. Дои:10.1103 / Physrev.138.a1727.
- ^ Берри, М. В. (1984). «Квантовые фазовые факторы, сопровождающие адиабатические изменения». Proc. R. Soc. А. 392 (1802): 45–57. Bibcode:1984RSPSA.392 ... 45B. Дои:10.1098 / rspa.1984.0023.
- ^ Herzberg, G .; Лонге-Хиггинс, Х.С. (1963). «Пересечение поверхностей потенциальной энергии в многоатомных молекулах». Обсуждения общества Фарадея. 35: 77. Дои:10.1039 / df9633500077.
- ^ Лонге-Хиггинс, Х.С. (1975). «Пересечение поверхностей потенциальной энергии в многоатомных молекулах». Proc. R. Soc. А. 344 (1637): 147–156. Bibcode:1975RSPSA.344..147L. Дои:10.1098 / RSPA.1975.0095.
- ^ Mead, C.A .; Трухлар, Д. Г. (1979). "Определение волновых функций движения ядер Борна-Оппенгеймера, включая осложнения из-за конических пересечений и одинаковых ядер". J. Chem. Phys. 70 (5): 2284–2296. Bibcode:1979ЖЧФ..70.2284М. Дои:10.1063/1.437734.
- ^ Kroto, H.W .; Heath, J. R .; O'Brien, S.C .; Curl, R. F .; Смолли Р. Э. (1985). "C60 - Бакминстерфуллерен ». Природа. 318 (6042): 162–163. Bibcode:1985Натура.318..162K. Дои:10.1038 / 318162a0.
- ^ Chancey, C.C .; О'Брайен, М. С. М (1997). Эффект Яна – Теллера в C60 и другие икосаэдрические комплексы. Принстон: Издательство Принстонского университета. ISBN 9780691044453.
- ^ Bednorz, J. G .; Мюллер, К. А. (1986). "Возможна высокая температура"c Сверхпроводимость в системе BaLaCuO ». Z. Phys. B. 64 (2): 189–193. Bibcode:1986ZPhyB..64..189B. Дои:10.1007 / bf01303701.
- ^ Миллис, А. Дж .; Shraiman, B.I .; Мюллер, Р. (1996). «Динамический эффект Яна – Теллера и колоссальное магнитосопротивление в Ла1-хSrИксMnO3". Phys. Rev. Lett. 77 (1): 175–178. arXiv:cond-mat / 9507084. Bibcode:1996ПхРвЛ..77..175М. Дои:10.1103 / PhysRevLett.77.175. PMID 10061800.
- ^ Лир, А. Д. (1963). «Топологические аспекты проблемы конформационной устойчивости .1. Вырожденные электронные состояния». J. Phys. Chem. 67 (2): 389–+. Дои:10.1021 / j100796a043.
- ^ Хэм, Ф. С. (1968). «Влияние линейной связи Яна – Теллера на парамагнитный резонанс в 2Имущество". Физический обзор. 166 (2): 307–321. Bibcode:1968ПхРв..166..307Х. Дои:10.1103 / PhysRev.166.307.
- ^ Йейтс, JH; Питцер, RM (1979). «Молекулярные и электронные структуры трифторидов переходных металлов». J. Chem. Phys. 70 (9): 4049–4055. Bibcode:1979ЖЧФ..70.4049Г. Дои:10.1063/1.438027.
- ^ Deeth, R.J .; Хитчман, М.А. (1985). «Факторы, влияющие на ян-теллеровские искажения в шестикоординатных комплексах меди (II) и низкоспинового никеля (II)». Неорг. Chem. 25 (8): 1225–1233. Дои:10.1021 / ic00228a031.
- ^ Ландау, Л. Д. (1933). "Über die Bewegung der Elektronen в Kristallgitter". Phys. Z. Sowjetunion. 3: 644–645.
- ^ Ганин, А. Я; Takabayashi, Y .; Химяк, Ю.З .; Маргадонна, S .; Tamai, A .; Россейнский, М. Дж; Прасидес, К. (2008). «Объемная сверхпроводимость при 38 К в молекулярной системе». Nat. Матер. 7 (5): 367–71. Bibcode:2008НатМа ... 7..367Г. Дои:10.1038 / nmat2179. PMID 18425134.
- ^ Гуннарссон, О. (1997). «Сверхпроводимость в фуллеридах». Ред. Мод. Phys. 69 (2): 575–606. arXiv:cond-mat / 9611150. Bibcode:1997РвМП ... 69..575Г. Дои:10.1103 / RevModPhys.69.575.
- ^ Zadik, Ruth H .; Такабаяси, Ясухиро; Клупп, Дьёнджи; Colman, Ross H .; Ганин, Алексей Юрьевич .; Поточник, Антон; Йеглич, Петр; Арчон, Денис; Матус, Петер; Камарас, Каталин; Касахара, Юичи; Иваса, Йошихиро; Fitch, Andrew N .; Охиси, Ясуо; Гарбарино, Гастон; Като, Кеничи; Россейнский, Мэтью Дж .; Prassides, Kosmas (2015). «Оптимизированная нетрадиционная сверхпроводимость в молекулярном ян-теллеровском металле». Sci. Adv. 1 (3): 500059. Bibcode:2015SciA .... 1E0059Z. Дои:10.1126 / sciadv.1500059. ЧВК 4640631. PMID 26601168.
- ^ Dunitz, J. D .; Оргель, Л. Э. (1957). «Электронные свойства оксидов переходных металлов - I: Нарушения кубической симметрии». J. Phys. Chem. Твердые тела. 3 (1): 20–29. Bibcode:1957JPCS .... 3 ... 20D. Дои:10.1016/0022-3697(57)90043-4.
- ^ МакКлюр, Д. С. (1957). «Распределение катионов переходных металлов в шпинелях». J. Phys. Chem. Твердые тела. 3 (3): 311–317. Bibcode:1957JPCS .... 3..311M. Дои:10.1016/0022-3697(57)90034-3.
- ^ Канамори Дж. (1960). «Кристаллическое искажение в магнитных соединениях». J. Appl. Phys. 31 (5): S14 – S23. Bibcode:1960JAP .... 31S..14K. Дои:10.1063/1.1984590.
- ^ Геринг, Г. А .; Геринг, К. А. (1975). «Кооперативные эффекты Яна – Теллера». Rep. Prog. Phys. 38 (1): 1. Bibcode:1975РПФ ... 38 .... 1Г. Дои:10.1088/0034-4885/38/1/001.
- ^ Kaplan, M.D .; Вехтер, Б.Г. (1995). Кооперативные явления в ян-теллеровских кристаллах. Нью-Йорк: Пленум Пресс. ISBN 978-1-4615-1859-4.
- ^ Lee, J. H .; Delaney, K. T .; Bousquet, E .; Spaldin, N.A .; Рабе, К. М. (2013). "Сильная связь искажения Яна – Теллера с вращением кислородного октаэдра и функциональными свойствами в эпитаксиально деформированном орторомбическом LaMnO.3". Phys. Ред. B. 88 (17): 174426. arXiv:1307.3347. Bibcode:2013PhRvB..88q4426L. Дои:10.1103 / PhysRevB.88.174426.
- ^ Kugel, K. I .; Хомский, Д. И. (1982). «Эффект Яна – Теллера и магнетизм - соединения переходных металлов». Сов. Phys. УСП. 25 (4): 231–256. Дои:10.3367 / UFNr.0136.198204c.0621.
внешняя ссылка
- Серия международных симпозиумов (в основном проводимых раз в два года) посвящена актуальным проблемам и современным разработкам в этой области, самые последние из которых
- Конференции проходят под наблюдением и под руководством международный руководящий комитет JT.
- Проиллюстрирована разница между реальным вращением и псевдовращением молекулы фуллерена. здесь.





















