Логическая форма (лингвистика) - Logical form (linguistics)

Эта статья о концепции в порождающая грамматика. Для более широкой концепции см. логическая форма.
Часть набор на
Лингвистика
Подполя
Грамматические теории
Темы
Портал Портал

В порождающая грамматика и связанных подходов, логическая форма (LF,) языкового выражения - это вариант его синтаксической структуры, который подвергается семантическая интерпретация. Он отличается от фонетическая форма структура, соответствующая произношению предложения. Эти отдельные представления постулируются для объяснения способов, которыми значение выражения может быть частично независимым от его произношения, например двусмысленность. LF - один из краеугольных камней классического генеративного подхода к интерфейсу синтаксис-семантика. Однако он не используется в Лексическая функциональная грамматика и Грамматика структуры фраз, управляемой головой, а также некоторые современные варианты генеративного подхода.

Синтаксический интерфейс с семантикой

Понятие логической формы было первоначально изобретено с целью определения квантификатор объем. По мере развития теории минималистской программы все выходные условия, такие как тета-критерий, фильтр наблюдений, подчиненность и теория связывания, рассматриваются на уровне НЧ. Изучение LF шире, чем изучение синтаксис.[1]

Понятие объема

Определение объема было введено в начале развития науки о логических формах. Область действия оператора - это область, в которой он может влиять на интерпретацию других выражений. Другими словами, оператор имеет область действия или влияет на интерпретацию других фраз только в пределах своей собственной области. Три неоспоримых примера области, влияющей на некоторые аспекты интерпретации: квантор-квантор, квантор-местоимение, квантификатор-элемент с отрицательной полярностью.

В случаях, когда отрицание имеет неопределенный артикль в своем объеме, это влияет на интерпретацию читателя. Читатель не может сделать вывод о существовании соответствующей сущности. Если отрицание (или фраза отрицания) находится в пределах области квантификатора субъекта, отрицание не зависит от квантификатора.[2]Если количественное выражение1 (QE1) находится в области QE2, но не наоборот, QE1 должно иметь узкую область действия; если оба находятся в сфере владения другого, структура потенциально неоднозначна. Если ни одно из QE не находится в сфере владения другого, они должны интерпретироваться независимо.[3] Эти предположения объясняют случаи, когда прямой объект основного предложения не находится в области встроенного субъекта. Например, что каждый мальчик расстроил учителя, его нельзя интерпретировать как на каждого мальчика, возможно, найдется другой учитель, которого расстроило то, что мальчик ушел. Единственная доступная интерпретация состоит в том, что один единственный учитель был расстроен.[2]

Все любят одного и того же
У всех есть кто-то, кого они любят, не обязательно один и тот же человек

Мотивация неоднозначности

В синтаксисе LF существует для структурного описания некоторых видов семантических неоднозначностей.

пример

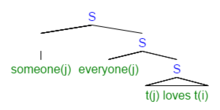
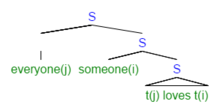
Все кого-то любят.

Это предложение семантически неоднозначно. В частности, он содержит объем двусмысленность. Эта неоднозначность не может быть разрешена в структуре поверхности, поскольку кто то, находясь в фразовый глагол, должен быть ниже в структуре, чем каждый. Этот случай иллюстрирует тот общий факт, что естественный язык недостаточно указано для строгого логического смысла. Роберт Мэй приводил доводы в пользу постулирования LF отчасти для того, чтобы объяснить такую ​​двусмысленность (среди других мотивов). В LF предложение выше будет иметь два возможных структурных представления, по одному для каждого возможного чтения объема, чтобы учесть неоднозначность посредством структурной дифференциации. В этом смысле он похож на, но не такой, как, логическая форма в логика.[4]

Количественная оценка

Ключевые исторические события

Дискуссия о количественной оценке ведется с 1970-х годов. В 1974 г. Ричард Монтегю утверждал, что грамматика для небольшого фрагмента английского языка содержит логико-синтаксические и семантические устройства для обработки практически любого явления масштаба.[5] Инструмент, на который он в основном полагался, - это категориальный синтаксис с функциональным применением; с точки зрения последних формулировок его можно считать минималистским синтаксисом с Объединить только. Однако этот подход не позволяет делать прогнозов для некоторых примеров с обратной областью видимости (широкий диапазон в объект позиция).

Например, все кого-то любят.

Если в соответствующей части предложения нет взаимодействия с областью видимости, выбор любого из них не показывает никакой разницы в семантике.

Спустя некоторое время Мэй предложил другую идею.[6] В отличие от Монтегю, Мэй не предлагал никакого синтаксиса, генерирующего поверхностную строку. Он предложил правило под названием Quantifier Raising (QR), которое объясняет, что операции движения белое движение продолжают работать на уровне LF, и каждая фраза продолжает иметь квантор в своей области. Мэй предположила, что QR применяется ко всем без исключения фразам-кванторам.

Изучение квантификации продолжалось в 1980-х годах. В отличие от Мэй и Монтегю, было высказано предположение, что независимо мотивированная структура фразы, такая как относительное предложение, накладывает ограничение на варианты области действия.[7]

Ограниченность этого предложения несколько ограничивает QR. Мэй также заметил асимметрию субъект-объект в отношении взаимодействия белых слов и фраз-кванторов.[8] Модифицированная версия его прошлой работы, в которой QR определяет объем квантификатора, но не устраняет неоднозначность, была поднята. Чтобы регулировать взаимодействие, также был поднят принцип области действия, согласно которому, если два оператора управляют друг другом, их можно интерпретировать в любом порядке области действия. Однако в итоге от этого решения отказались.

Так как Минимализм появились в 1990-х годах, больше исследований было связано с минималистским синтаксисом.[9] Стратегия исправления ситуации состоит в том, чтобы исключить QR, и ожидаемый объем будет побочным продуктом полностью независимых грамматических процессов.[10] Другая стратегия - изменить QR и показать, что его можно вписать в минималистскую структуру.[11][12]

Количественные выражения существительных

Дэнни Фокс обсуждает синтаксические позиции QNP как способ представления и иллюстрации основных семантических и синтаксических отношений, обнаруженных в LF.[13] Рассматривая значение QNP по отношению к данному им свойству или их предикату, мы можем вывести значение всего предложения.

а. Девушка высокая.

б. Многие девушки высокого роста.

c. Каждая девушка высокая.

d. Нет девушки высокой.[13]

Чтобы понять логическую форму этих примеров, важно определить, какие основные предикат есть и какие сегменты составляют QNP. В этих примерах предикат высокий, а QNP - это девушка, много девушек, каждая девушка и ни одна девушка. Логический смысл этих предложений указывает на то, что свойство высокий рост приписывается некоторой форме QNP, относящейся к девушке. Наряду с QNP и предикатом существует также вывод значения истинности. Либо значение истины истинно для высокого человека, либо значение истины - ложь.[13]

В каждом из приведенных выше примеров будут разные условия, которые делают утверждение истинным в соответствии с квантификатором, который предшествует девушке.[13]

Условия истинности:

Пример а. Девушка имеет ценность истины верно тогда и только тогда, когда (если только ) хотя бы одна девушка высокая.
Этот квантификатор удовлетворяет 1 случай высокой девушки.

Пример б. Многие девушки имеет ценность истины верно, если и только если есть много высоких девушек.
Этот количественный показатель удовлетворяется более чем одним случаем высокой девушки.

Пример c. Каждая девушка имеет ценность истины верно, если и только если каждая девушка высокая.
Этот квантификатор требует от всех девочек, что каждый случай, когда человек является женщиной, должен быть высоким.

Пример d. Нет девушки имеет ценность истины верно, если и только если нет девушки высокой.
Этот количественный показатель требует от всех девочек, что для всех случаев, когда лицо женщины, она не должна быть высокой.[13]

В синтаксическом дереве структура представлена ​​так: аргумент QNP всегда является сестрой QNP ".[13]

Wh-движение

В лингвистике WH-фразы - это операторы, связывающие переменные в LF, как и другие количественные словосочетания с существительными. Интерпретации области действия могут быть ограничены синтаксическими ограничениями, как показано в LF, когда речь идет о области применения WH-фраз и квантификаторов. Когда белое движение с позиции субъекта это однозначно, но когда движение происходит с позиции объекта, оно неоднозначно.[8]

Примеры

1) Что все купили за Макса?

[Что?2 [S все3 [S e3 купил е2 для макс]
(Две возможные интерпретации: что сделали все
коллективно покупать, против индивидуально купить)

2) Кто купил все для Макса?

[S ’who3 [S все2 [S e3 купил е2 для макс]
(Возможна только одна интерпретация.)

Этот пример демонстрирует эффект условия ограничения пути (PCC). A'-путь - это линия доминирующих узлов, которые идут от трассы к A'-связующему, управляющему c. Если два пути A пересекаются, то один должен содержаться в другом. Если пути перекрываются, но один из них не входит в другой, то это неправильно. Пути (2) перекрываются, нарушая PCC, поэтому, чтобы получить грамматическую структуру LF, все должно соединиться с VP. Тогда структура LF становится:

ПРЕДСТАВИТЕЛЬСТВО LF:
[s ’who3 [s e3 [вп за все2 [vp купил e2 для макс]

Кросс-лингвистические примеры

венгерский язык

Öt orvos minden betegnek kevés új tablettát írt fel.
пять врачей на каждого пациента - Дат несколько новых таблеток - написал
«Есть пять врачей x таких, что каждому пациенту y x прописал y несколько новых таблеток».
* Öt orvos kevés betegnek minden új tablettát írt fel.
пять докторов, несколько пациентов - Даты каждой новой таблетки - написал Акк.
«Есть пять докторов x таких, что какому-то пациенту y, x прописал y новую таблетку».

В предложении «Пять врачей прописали каждому пациенту несколько новых таблеток»., объем на венгерском языке в значительной степени устраняется линейным порядком кванторов на поверхности. Следует иметь в виду два факта: (1) линейный порядок не достигается сложением кванторов в желаемом порядке, что противоречит предсказаниям, сделанным Монтегю или теорией Мэя; (2) линейный порядок не определяется регистром или грамматическими функциями, что подтверждает предсказание теории Хорнштейна. [14]

Китайский

1. Yaoshi liangge nuren du guo meiben shu ...
если две женщины прочитают Asp каждую книгу
я. "если есть две женщины, которые читают каждую книгу ..."
II. «* если каждую книгу читают две женщины ...»
2. Yaoshi liangge xiansuo bei meigeren zhaodao ...
если бы все нашли две подсказки
я. "если есть две улики, которые найдет каждый ..."
II. "если для каждого есть два ключа, которые она или он найдет ..."

В китайском языке подчеркивается важность А-цепей. В некоторых примерах сфера действия в китайском языке определяется позициями падежей. [15] В этом примере активное предложение имеет только подлежащее, но пассивное предложение неоднозначно. У активного предложения есть только одно толкование: если две женщины читают каждую книгу, что является предметом широкого диапазона. По словам Ауна и Ли, у китайцев нет внутренних подчиненных, поэтому Liangge Nuren не может быть реконструирован в LF. Так что у предложения нет двусмысленного толкования. Однако у пассивного предложения есть две интерпретации: 1. Все находят одни и те же две подсказки; 2. Каждый находит две подсказки, а две подсказки могут быть разными. Это потому Liangge Xiansuo находится в позиции внутреннего дополнения VP, то в LF его можно реконструировать. Итак, у пассивного предложения есть две разные интерпретации.

английский

На каждое дерево залез мальчик.
я. Одинокий мальчик залез на все деревья.
II. Для каждого дерева есть мальчик, который может быть разным для каждого дерева, который залез на дерево X.

Эта фраза неоднозначна в том смысле, что ее можно интерпретировать как существительное «мальчик», относящееся к конкретному человеку или к другому человеку для каждого экземпляра «дерево» под квантификатором «каждый».[13] Интерпретация, что один мальчик взобрался на все деревья, имеет широкий диапазон, в то время как другая интерпретация, что для каждого дерева есть мальчик, который может быть разным для каждого дерева, имеет узкую область.

Смотрите также

использованная литература

  1. ^ Сабольчи 2003, с. 607, 633.
  2. ^ а б Сабольчи 2003.
  3. ^ Ioup 1975 г..
  4. ^ Ханна 2006 С. 50–51.
  5. ^ Монтегю 1974.
  6. ^ Май 1977 г..
  7. ^ Рейнхарт 1983.
  8. ^ а б Май 1985 г..
  9. ^ Хомский 1993.
  10. ^ Хорнштейн 1995.
  11. ^ Бегелли 1993.
  12. ^ Бегелли и Стоуэлл 1997.
  13. ^ а б c d е ж г Хендрик 2003.
  14. ^ Сабольчи 2002.
  15. ^ Аун и Ли 1993.

Список используемой литературы

  • Аун, Джозеф; Ли, Янь-хуэй Одри (1993). Синтаксис области видимости. MIT Press. ISBN  9780262011334.CS1 maint: ref = harv (ссылка на сайт)
  • Кук, Вивиан Джеймс; Ньюсон, Марк (2007). Универсальная грамматика Хомского: введение (3-е изд.). Вили-Блэквелл. ISBN  978-1-4051-1186-7.
  • Коллиндж, Невилл Эдгар (1990). Энциклопедия языка. Рутледж. ISBN  9780415020640.CS1 maint: ref = harv (ссылка на сайт)
  • Коркоран, Дж. Схемы: понятие схемы в истории логики. Бюллетень символической логики 12: 219-40.CS1 maint: ref = harv (ссылка на сайт)
  • Ханна, Роберт (2006). Рациональность и логика. MIT Press. С. 50–51. ISBN  978-0-262-08349-2.CS1 maint: ref = harv (ссылка на сайт)
  • Хендрик, Рэндалл (2003). Минималистичный синтаксис. Оксфорд, Великобритания: Блэквелл. ISBN  0-631-21941-2.CS1 maint: ref = harv (ссылка на сайт)
  • Хорнштейн, Норберт (1995). Логическая форма: от ГБ до минимализма. Блэквелл. ISBN  978-0-631-18942-8.CS1 maint: ref = harv (ссылка на сайт)
  • Мэй, Роберт (1985). Логическая форма: ее структура и происхождение. MIT Press. ISBN  978-0-262-63102-0.CS1 maint: ref = harv (ссылка на сайт)
  • Ухалла, Дж. (1999). Введение в трансформационную грамматику (2-е изд.). Издательство Арнольд.CS1 maint: ref = harv (ссылка на сайт)
  • Сабольчи, Анна (2003). Справочник по современной синтаксической теории. Мальден, Массачусетс. ; Оксфорд, Великобритания: Blackwell Pub. С. 607, 633. ISBN  1405102535.CS1 maint: ref = harv (ссылка на сайт)
  • Вебельхут, Герт (1994). Правительственная и обязательная теория. Оксфорд: Блэквелл. С. 127–175. ISBN  0-631-18059-1.CS1 maint: ref = harv (ссылка на сайт)
  • Мэй, Роберт (1993). Логическая форма: ее структура и происхождение. MIT Press. С. 1, 30. ISBN  0262132044.CS1 maint: ref = harv (ссылка на сайт)

внешняя ссылка