Максимальная ровность - Maximal evenness

В крупный масштаб максимально ровный. Например, для каждого общего интервала секунды есть только два возможных конкретных интервала: 1 полутон (второстепенная секунда) или 2 полутона (большая секунда).
В гармоническая минорная гамма не максимально ровно. Для общего интервала в секунду, а не только для двух конкретных интервалов, шкала содержит три: 1, 2 и 3 (увеличенная секунда ) полутонов.

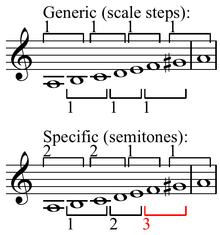
В гамма (музыка) теория а максимально ровный набор (масштаб) - это тот, в котором каждый общий интервал имеет одно или два последовательных целых числа определенные интервалы - другими словами, шкала, ноты которой (шт.) «разложены насколько возможно». Это свойство было впервые описано Джоном Клафом и Джеком Даутеттом.[1]. Клаф и Даутетт также ввели алгоритм максимальной четности. Для хроматической мощности c и набор ПК мощность d максимально четное множество

куда k колеблется от 0 до d - 1 и м, 0 ≤ м ≤ c - 1 фиксируется, а пара спинок выполняет функцию пола. Прекрасное обсуждение этих концепций можно найти в книге Тимоти Джонсона о математических основах теории диатонических шкал.[2] Джек Даутетт и Ричард Кранц ввели в математическую литературу максимально ровные множества.[3][4]

Говорят, что шкала имеет Собственность Майхилла если каждый общий интервал входит в два определенный интервал размеров, а шкала со свойством Майхилла называется правильно сформированная шкала.[5] В диатоническая коллекция является одновременно хорошо сформированной шкалой и максимально ровной. В полнотонная шкала также максимально четный, но он плохо сформирован, поскольку каждый общий интервал имеет только один размер.

Максимальная четкость второго порядка - максимальная четность подколлекции большего набора, максимально четная. Диатонические трезвучия и септаккорды обладают максимальной ровностью второго порядка, будучи максимально ровными в отношении максимально ровной диатонической гаммы, но не максимально ровны в отношении хроматической гаммы. (там же, с.115) Это вложенное качество напоминает Фред Лердал с[6] "редукционный формат" для пространство поля снизу вверх:

CEграммC
CDEFграммАBC
CD ♭DE ♭EFF♯граммА ♭АB ♭BC
(Лердал, 1992)

В динамичный подход, вращение концентрические круги и построены максимально четные итерированные множества. Этот подход имеет значение в Неориманновская теория, и приводит к интересным связям между диатонический и хроматический теория.[7] Эммануэль Амио открыл еще один способ определять максимально ровные множества, используя дискретные преобразования Фурье.[8][9]

Кэри, Норман и Клампит, Дэвид (1989). «Аспекты правильно сформированных гамм», Music Theory Spectrum 11: 187–206.

Рекомендации

  1. ^ Клаф, Джон; Даутетт, Джек (1991). «Максимально ровные наборы». Журнал теории музыки (35): 93-173.
  2. ^ Джонсон, Тимоти (2003). Основы диатонической теории: математический подход к основам музыки. Key College Publishing. ISBN  1-930190-80-8.
  3. ^ Даутетт, Джек; Кранц, Ричард (2007). «Максимально равные множества и конфигурации: общие темы в математике, физике и музыке». Журнал комбинаторной оптимизации. 14: 385-410.
  4. ^ Даутетт, Джек; Кранц, Ричард (2007). «Обеденные столы и концентрические круги: гармония математики, музыки и физики». Журнал математики колледжа. 39 (3): 203-211.
  5. ^ Кэри, Норман; Клампитт, Дэвид (1989). «Аспекты хорошо сформированных весов». Музыка Теория Спектр. 11: 187-206.
  6. ^ Лердал, Фред (1992). «Когнитивные ограничения на композиционные системы». Обзор современной музыки. 6 (2): 97-121.
  7. ^ Даутетт, Джек (2008). «Симметрия точки фильтра и динамическое ведение голоса». Музыка и математика: аккорды, сборники и трансформации. Истмен Исследования в области музыки: 72-106. Эд. Дж. Даутетт, М. Хайд и К. Смит. Университет Рочестера, Нью-Йорк. ISBN  1-58046-266-9.
  8. ^ Армиот, Эммануэль (2007). «Дэвид Левин и максимально ровные сеты». Журнал математики и музыки. 1 (3): 157-172.
  9. ^ Армиот, Эммануэль (2016). Музыка в пространстве Фурье: дискретное преобразование Фурье в теории музыки. Springer. ISBN  9783319455808.