Недетерминированный конечный автомат - Nondeterministic finite automaton

В теория автоматов, а конечный автомат называется детерминированный конечный автомат (DFA), если
- каждый из его переходов однозначно определяется его исходным состоянием и входным символом, и
- чтение входного символа требуется для каждого перехода состояния.
А недетерминированный конечный автомат (NFA), или недетерминированный конечный автомат, не нужно соблюдать эти ограничения. В частности, каждый DFA также является NFA. Иногда термин NFA используется в более узком смысле, имея в виду NFA, не DFA, но не в этой статье.
С использованием алгоритм построения подмножества, каждый NFA может быть переведен в эквивалентный DFA; то есть DFA, распознающий то же формальный язык.[1]Как и DFA, NFA распознают только обычные языки.
NFA были введены в 1959 г. Майкл О. Рабин и Дана Скотт,[2] которые также показали свою эквивалентность DFA. NFA используются при реализации обычные выражения: Конструкция Томпсона - это алгоритм компиляции регулярного выражения в NFA, который может эффективно выполнять сопоставление с образцом в строках. Наоборот, Алгоритм Клини может использоваться для преобразования NFA в регулярное выражение (размер которого обычно экспоненциальный во входном автомате).
NFA были обобщены по-разному, например, недетерминированные конечные автоматы с ε-ходами, конечные преобразователи, выталкивающие автоматы, чередующиеся автоматы, ω-автоматы, и вероятностные автоматы. Помимо DFA, существуют другие известные частные случаи NFA. однозначные конечные автоматы (УФА) и самопроверяющиеся конечные автоматы (SVFA).
Неформальное введение
Есть несколько неформальных объяснений, которые эквивалентны.
- NFA, похожий на DFA, потребляет строку входных символов. Для каждого входного символа он переходит в новое состояние до тех пор, пока все входные символы не будут использованы. На каждом шаге автомат произвольно выбирает один из подходящих переходов. Если существует какой-то «счастливый прогон», то есть некоторая последовательность выборов, приводящая к состоянию принятия после полного использования ввода, он принимается. В противном случае, т.е. если никакая последовательность выбора не может потреблять весь ввод[3] и привести к состоянию принятия, ввод отклоняется.[4]:19[5]:319
- Опять же, NFA использует строку входных символов один за другим. На каждом этапе, когда применимы два или более перехода, он «клонирует» себя в соответствующее количество копий, каждая из которых следует за другим переходом. Если переход невозможен, текущая копия находится в тупике и «умирает». Если после использования всего ввода любая из копий находится в состоянии принятия, ввод принимается, иначе он отклоняется.[4]:19–20[6]:48[7]:56
Формальное определение
Для более элементарного введения формального определения см. теория автоматов.
Автомат
An NFA представлен формально 5-кратный,, состоящий из
- конечный набор государств .
- конечный набор входные символы .
- функция перехода : .
- ан начальный (или Начните) штат .
- набор состояний отличился как принимая (или окончательный) состояния .
Вот, обозначает набор мощности из .
Признанный язык
Учитывая NFA , его признанный язык обозначается , и определяется как набор всех строк в алфавите которые принимаются .
Примерно соответствует над неформальные объяснения, есть несколько эквивалентных формальных определений строки принимается :
- принимается, если последовательность состояний, , существует в такой, что:
- , для
- .
- На словах первое условие говорит о том, что машина запускается в стартовом состоянии. . Второе условие говорит, что для каждого символа строки , машина перейдет из состояния в состояние в соответствии с функцией перехода . Последнее условие говорит о том, что машина принимает если последний ввод заставляет машину останавливаться в одном из состояний приема. Для того чтобы быть принятым , не требуется, чтобы каждая последовательность состояний заканчивалась в состоянии приема, достаточно, если это так. В противном случае, т.е. если вообще невозможно получить от в состояние из следуя , говорят, что автомат отвергает Струна. Набор струн принимает язык признанный от и этот язык обозначается .[5]:320[6]:54
- В качестве альтернативы, принимается, если , где определено рекурсивно от:
- где - пустая строка, а
- для всех .
- Прописью, это набор всех состояний, достижимых из состояния потребляя строку . Струна принимается, если какое-либо принимающее состояние в может быть достигнуто из начального состояния потребляя .[4]:21[7]:59
Начальное состояние
В приведенном выше определении автомата используется единственное начальное состояние, что не обязательно. Иногда NFA определяются набором начальных состояний. Легко строительство который переводит NFA с несколькими начальными состояниями в NFA с одним начальным состоянием, что обеспечивает удобную запись.
пример
 В диаграмма состояний для M. Он не детерминирован, поскольку в состоянии п чтение 1 может привести к п или чтобы q. |  Все возможные прогоны M на входной строке «10». |
 Все возможные прогоны M во входной строке «1011». Этикетка дуги: символ ввода, метка узла: штат, зеленый: начальное состояние, красный: принимающее состояние (а). | |
Следующий автомат , с двоичным алфавитом, определяет, заканчивается ли вход 1. где переходная функция можно определить этим таблица переходов состояний (см. верхний левый рисунок):
Ввод государство | 0 | 1 |
|---|---|---|
Поскольку набор содержит более одного состояния, недетерминирован. можно описать обычный язык предоставленный регулярное выражение (0|1)*1.
Все возможные последовательности состояний для входной строки «1011» показаны на нижнем рисунке. Строка принимается поскольку одна последовательность состояний удовлетворяет приведенному выше определению; неважно, что другие последовательности этого не делают. Картинку можно интерпретировать двумя способами:
- Что касается над объяснение "удачный ход", каждый путь на картинке обозначает последовательность вариантов выбора .
- Что касается объяснения "клонирования", каждый вертикальный столбец показывает все клоны в данный момент времени несколько стрелок, исходящих от узла, указывают на клонирование, узел без исходящих стрелок указывает на «смерть» клона.
Возможность прочитать одну и ту же картинку двумя способами также указывает на эквивалентность обоих приведенных выше объяснений.
- Учитывая первое из над формальные определения, "1011" принято, так как при чтении может пересекать последовательность состояний , который удовлетворяет условиям с 1 по 3.
- Что касается второго формального определения, вычисление снизу вверх показывает, что , следовательно , следовательно , следовательно , и, следовательно ; так как это множество не отделено от , строка «1011» принимается.
Напротив, строка "10" отклоняется (все возможные последовательности состояний для этого входа показаны на верхнем правом рисунке), поскольку нет возможности достичь единственного принимающего состояния, , прочитав последний символ 0. В то время как может быть достигнуто после использования начальной «1», это не означает, что ввод «10» принят; скорее, это означает, что будет принята входная строка «1».
Эквивалентность DFA
А детерминированный конечный автомат (DFA) можно рассматривать как особый вид NFA, в котором для каждого состояния и алфавита функция перехода имеет ровно одно состояние. Таким образом, ясно, что каждый формальный язык которые могут быть распознаны DFA, могут быть распознаны NFA.
И наоборот, для каждого NFA существует такой DFA, который распознает один и тот же формальный язык. DFA может быть построен с использованием конструкция электростанции.
Этот результат показывает, что NFA, несмотря на их дополнительную гибкость, не могут распознавать языки, которые не могут быть распознаны некоторыми DFA. Это также важно на практике для преобразования простых в создании NFA в более эффективно исполняемые DFA. Однако если в NFA п утверждает, что в итоговом DFA может быть до 2п штатов, что иногда делает конструкцию нецелесообразной для крупных ЯОС.
NFA с ε-ходами
Недетерминированный конечный автомат с ε-движениями (NFA-ε) является дальнейшим обобщением на NFA. Этот автомат заменяет функцию перехода на ту, которая позволяет пустой строки ε в качестве возможного входа. Переходы без использования входного символа называются ε-переходами. На диаграммах состояний они обычно обозначаются греческой буквой ε. ε-переходы обеспечивают удобный способ моделирования систем, текущие состояния которых точно не известны: т. е. если мы моделируем систему и неясно, должно ли текущее состояние (после обработки некоторой входной строки) быть q или q ', тогда мы можем добавить ε-переход между этими двумя состояниями, таким образом переводя автомат в оба состояния одновременно.
Формальное определение
An NFA-ε представлен формально 5-кратный, , состоящий из
- конечный набор из состояния
- конечный набор входные символы называется алфавит
- переход функция
- ан начальный (или Начните ) штат
- набор состояний отличился как принимая (или окончательный) состояния .
Вот, обозначает набор мощности из а ε обозначает пустую строку.
ε-замыкание состояния или набора состояний
Для государства , позволять обозначают множество состояний, достижимых из следуя ε-переходам в переходной функции , т.е. если есть последовательность состояний такой, что
- ,
- для каждого , и
- .
известен как ε-замыкание из .
ε-замыкание также определено для набора состояний. Ε-замыкание множества состояний, , NFA определяется как набор состояний, достижимых из любого состояния в следующие ε-переходы. Формально для , определить .
Принимающие состояния
Позволять быть строкой в алфавите . Автомат принимает Струна если последовательность состояний,, существует в со следующими условиями:
- где для каждого , и
- .
На словах первое условие говорит, что машина запускается в состоянии, достижимом из начального состояния. через ε-переходы. Второе условие говорит, что после прочтения , машина выполняет переход от к , а затем принимает любое количество ε-переходов согласно двигаться от к . Последнее условие говорит о том, что машина принимает если последний ввод заставляет машину останавливаться в одном из состояний приема. В противном случае говорят, что автомат отвергает Струна. Набор струн принимает язык признанный от и этот язык обозначается .
пример
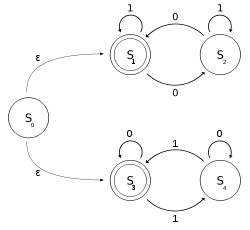
Позволять быть NFA-ε с двоичным алфавитом, который определяет, содержит ли вход четное количество нулей или четное количество единиц. Обратите внимание, что 0 вхождений также является четным числом вхождений.
В формальных обозначениях пусть где переходное отношение можно определить этим таблица переходов состояний:
Ввод государство | 0 | 1 | ε |
|---|---|---|---|
| S0 | {} | {} | {S1, S3} |
| S1 | {S2} | {S1} | {} |
| S2 | {S1} | {S2} | {} |
| S3 | {S3} | {S4} | {} |
| S4 | {S4} | {S3} | {} |
можно рассматривать как союз двух DFA: один со состояниями а другой с состояниями . Язык можно описать обычный язык дано этим регулярное выражение (1 * (01 * 01 *) *) ∪ (0 * (10 * 10 *) *). Определим используя ε-ходы, но можно определить без использования ε-движений.
Эквивалентность NFA
Чтобы показать, что NFA-ε эквивалентно NFA, сначала отметим, что NFA является частным случаем NFA-ε, поэтому остается показать, что для каждого NFA-ε существует эквивалентный NFA.
Позволять быть NFA-ε. NFA эквивалентно , где для каждого и , .
Таким образом, NFA-ε эквивалентно NFA. Поскольку NFA эквивалентно DFA, NFA-ε также эквивалентно DFA.
Свойства закрытия

NFA называются закрыт под а (двоичный /унарный ), если NFA распознают языки, полученные в результате применения операции к распознаваемым NFA языкам. NFA замыкаются при выполнении следующих операций.
- Союз (см. Рисунок)
- Пересечение
- Конкатенация
- Отрицание
- Клини закрытие
Поскольку NFA эквивалентны недетерминированному конечному автомату с ε-движениями (NFA-ε), указанные выше замыкания доказываются с использованием свойств замыкания NFA-ε. Вышеупомянутые свойства закрытия подразумевают, что NFA распознают только обычные языки.
NFA могут быть построены из любых регулярное выражение с помощью Алгоритм построения Томпсона.
Свойства
Машина запускается в указанном начальном состоянии и считывает строку символов из своего алфавит. Автомат использует функция перехода между состояниями Δ для определения следующего состояния с использованием текущего состояния и только что прочитанного символа или пустой строки. Однако «следующее состояние NFA зависит не только от текущего события ввода, но также и от произвольного числа последующих событий ввода. Пока эти последующие события не произойдут, невозможно определить, в каком состоянии находится машина».[8] Если, когда автомат закончил чтение, он находится в состоянии принятия, говорят, что NFA принимает строку, в противном случае говорят, что она отклоняет строку.
Набор всех строк, принимаемых NFA, является языком, который принимает NFA. Этот язык обычный язык.
Для каждого NFA a детерминированный конечный автомат (DFA) может принимать тот же язык. Следовательно, можно преобразовать существующий NFA в DFA с целью реализации (возможно) более простой машины. Это можно сделать с помощью конструкция электростанции, что может привести к экспоненциальному росту количества необходимых состояний. Для формального доказательства конструкции блока питания см. Конструкция Powerset статья.
Реализация
Есть много способов реализовать NFA:
- Преобразуйте в эквивалентный DFA. В некоторых случаях это может вызвать экспоненциальный рост числа состояний.[9]
- Держать установить структуру данных всех состояний, в которых в настоящее время может находиться NFA. При потреблении входного символа объединяться результаты функции перехода, примененной ко всем текущим состояниям, чтобы получить набор следующих состояний; если разрешены ε-перемещения, включить все состояния, достижимые таким перемещением (ε-замыкание). Каждый шаг требует не более s2 вычисления, где s - количество состояний NFA. При использовании последнего входного символа, если одно из текущих состояний является конечным, машина принимает строку. Строка длины п можно обработать вовремя О (нс2),[7]:153 и космос О(s).
- Создайте несколько копий. Для каждого n-стороннего решения NFA создает до копии машины. Каждый войдет в отдельное состояние. Если после использования последнего входного символа хотя бы одна копия NFA находится в состоянии приема, NFA примет. (Это тоже требует линейного хранения в зависимости от количества состояний NFA, поскольку для каждого состояния NFA может быть одна машина.)
- Явно распространяйте токены через структуру перехода NFA и сопоставляйте каждый раз, когда токен достигает конечного состояния. Это иногда полезно, когда NFA следует кодировать дополнительный контекст о событиях, вызвавших переход. (Для реализации, которая использует этот метод для отслеживания ссылок на объекты, посмотрите Tracematches.[10])
Применение NFA
NFA и DFA эквивалентны в том смысле, что если язык распознается NFA, он также распознается DFA, и наоборот. Установление такой эквивалентности важно и полезно. Это полезно, потому что создание NFA для распознавания данного языка иногда намного проще, чем создание DFA для этого языка. Это важно, поскольку NFA можно использовать для уменьшения сложности математической работы, необходимой для установления многих важных свойств в теория вычислений. Например, доказать гораздо проще закрывающие свойства из обычные языки используя NFA, а не DFA.
Смотрите также
- Детерминированный конечный автомат
- Двусторонний недетерминированный конечный автомат
- Выталкивающий автомат
- Машина Тьюринга
Заметки
- ^ Мартин, Джон (2010). Введение в языки и теорию вычислений. Макгроу Хилл. п. 108. ISBN 978-0071289429.
- ^ Рабин, М. О .; Скотт, Д. (апрель 1959 г.). «Конечные автоматы и проблемы их решения». Журнал исследований и разработок IBM. 3 (2): 114–125. Дои:10.1147 / rd.32.0114.
- ^ Последовательность выбора может привести к «тупику», когда для текущего входного символа переход невозможен; в этом случае он считается неудачным.
- ^ а б c Джон Э. Хопкрофт и Джеффри Д. Уллман (1979). Введение в теорию автоматов, языки и вычисления. Ридинг / МА: Эддисон-Уэсли. ISBN 0-201-02988-X.
- ^ а б Альфред В. Ахо, Джон Э. Хопкрофт и Джеффри Д. Ульман (1974). Разработка и анализ компьютерных алгоритмов. Ридинг / МА: Эддисон-Уэсли. ISBN 0-201-00029-6.
- ^ а б Майкл Сипсер (1997). Введение в теорию вычислений. Бостон / Массачусетс: PWS Publishing Co. ISBN 0-534-94728-X.
- ^ а б c Джон Э. Хопкрофт, Раджив Мотвани и Джеффри Д. Ульман (2003). Введение в теорию автоматов, языки и вычисления (PDF). Река Аппер Сэдл / Нью-Джерси: Эддисон Уэсли. ISBN 0-201-44124-1.
- ^ Бесплатный онлайн-словарь по вычислительной технике FOLDOC, Конечный автомат
- ^ http://cseweb.ucsd.edu/~ccalabro/essays/fsa.pdf
- ^ Аллан, К., Августинов, П., Кристенсен, А.С., Хендрен, Л., Кузинс, С., Лхотак, О., де Моор, О., Серени, Д., Ситтампалам, Г., и Тиббл, Дж. 2005 г. Добавление сопоставления трассировки со свободными переменными в AspectJ В архиве 2009-09-18 на Wayback Machine. В материалах 20-й ежегодной конференции ACM SIGPLAN по объектно-ориентированному программированию, системам, языкам и приложениям (Сан-Диего, Калифорния, США, 16–20 октября 2005 г.). ОПСЛА '05. ACM, Нью-Йорк, штат Нью-Йорк, 345-364.
использованная литература
- М. О. Рабин и Д. Скотт, "Конечные автоматы и их проблемы решения", Журнал исследований и разработок IBM, 3: 2 (1959) с. 115–125.
- Майкл Сипсер, Введение в теорию вычислений. PWS, Бостон. 1997 г. ISBN 0-534-94728-X. (см. раздел 1.2: Недетерминизм, стр. 47–63.)
- Джон Э. Хопкрофт и Джеффри Д. Уллман, Введение в теорию автоматов, языки и вычисления, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (См. Главу 2.)








































































