Координаты Риндлера - Rindler coordinates

В релятивистская физика, координаты гиперболически ускоренная система отсчета^{[H 1]}^[1] составляют важную и полезную карта координат представляющая часть квартиры Пространство-время Минковского.^[2]^[3]^[4]^[5] В специальная теория относительности, равномерно ускоряющаяся частица испытывает гиперболическое движение, для которого равномерно ускорение точка зрения в котором он находится в состоянии покоя, может быть выбран в качестве его надлежащая система отсчета. Явления в этой гиперболически ускоренной системе отсчета можно сравнить с эффектами, возникающими в однородной гравитационное поле. Для общего обзора ускорений в плоском пространстве-времени см. Ускорение (специальная теория относительности) и Правильная система отсчета (плоское пространство-время).

В этой статье скорость света определяется $c = 1$ , то инерциальные координаты находятся $(X, Y, Z, T)$ , а гиперболические координаты равны $(х, у, z, t)$ . Эти гиперболические координаты можно разделить на два основных варианта в зависимости от положения ускоренного наблюдателя: если наблюдатель находится в момент времени $Т = 0$ на позиции $Икс = 1 / α$ (с $α$ как постоянная правильное ускорение измеряется сопутствующим акселерометр ), то гиперболические координаты часто называют Координаты Риндлера с соответствующими Метрика Риндлера.^[6] Если наблюдатель находится во время $Т = 0$ на позиции $Икс = 0$ , то гиперболические координаты иногда называют Координаты Мёллера^[1] или же Координаты Коттлера-Мёллера с соответствующими Метрика Коттлера-Мёллера.^[7] Альтернативная диаграмма, часто связанная с наблюдателями в гиперболическом движении, получается с использованием Радар координаты^[8] которые иногда называют Координаты девушки.^[9]^[10] Как координаты Коттлера-Мёллера, так и координаты Ласса также обозначаются как координаты Риндлера.^[11]

Что касается истории, то такие координаты были введены вскоре после появления специальной теории относительности, когда они были изучены (полностью или частично) вместе с концепцией гиперболического движения: применительно к плоскому пространству-времени Минковского автор Альберт Эйнштейн (1907, 1912),^{[H 2]} Макс Борн (1909),^{[H 1]} Арнольд Зоммерфельд (1910),^{[H 3]} Макс фон Лауэ (1911),^{[H 4]} Хендрик Лоренц (1913),^{[H 5]} Фридрих Коттлер (1914),^{[H 6]} Вольфганг Паули (1921),^{[H 7]} Карл Боллерт (1922),^{[H 8]} Степан Мохорович (1922),^{[H 9]} Жорж Лемэтр (1924),^{[H 10]} Эйнштейн и Натан Розен (1935),^{[H 2]} Кристиан Мёллер (1943, 1952),^{[H 11]} Фриц Рорлих (1963),^[12] Гарри Ласс (1963),^[13] и в отношении как квартиры, так и искривленное пространство-время из общая теория относительности к Вольфганг Риндлер (1960, 1966).^[14]^[15] Подробнее и источники см. раздел по истории.

Характеристики рамы Риндлера

График Риндлера, для

{ displaystyle alpha = 0,5}

в уравнении (1а), нанесенный на диаграмму Минковского. Пунктирные линии - горизонты Риндлера.

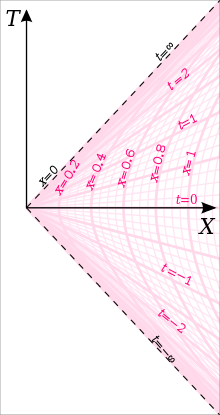
В мировая линия тела в гиперболическое движение имея постоянное собственное ускорение ${ displaystyle alpha}$ в ${ displaystyle X}$ -направление как функция подходящее время ${ Displaystyle тау}$ и быстрота ${ Displaystyle альфа тау}$ может быть дан^[16]

{ Displaystyle Т = Икс зп ( альфа тау), квад Икс = х ш ( альфа тау)}

куда ${ Displaystyle х = 1 / альфа}$ постоянно и ${ Displaystyle альфа тау}$ переменная, мировая линия напоминает гиперболу ${ displaystyle X ^ {2} -T ^ {2} = x ^ {2}}$ . Зоммерфельд^{[H 3]}^[17] показал, что уравнения могут быть переинтерпретированы путем определения ${ displaystyle x}$ как переменная и ${ Displaystyle альфа тау}$ как постоянный, так что он представляет одновременную «форму покоя» тела в гиперболическом движении, измеренную сопутствующим наблюдателем. Используя собственное время наблюдателя как время всего гиперболически ускоренного кадра, установив ${ Displaystyle тау = т}$ , формулы преобразования между инерциальными координатами и гиперболическими координатами, следовательно, будут:^[6]^[9]

{ Displaystyle Т = Икс зп ( альфа т), четырехъядерных X = х соз ( альфа т), четырехъядерных Y = y, четырехъядерных Z = z}

(1а)

с обратным

{ displaystyle t = { frac {1} { alpha}} operatorname {arctanh} left ({ frac {T} {X}} right), quad x = { sqrt {X ^ {2 } -T ^ {2}}}, quad y = Y, quad z = Z}

Дифференцированный и вставлен в метрику Минковского ${ displaystyle ds ^ {2} = - dT ^ {2} + dX ^ {2} + dY ^ {2} + dZ ^ {2}}$ , то метрика в гиперболически ускоренной системе отсчета следует

{ displaystyle ds ^ {2} = - ( alpha x) ^ {2} dt ^ {2} + dx ^ {2} + dy ^ {2} + dz ^ {2}}

(1b)

Эти преобразования определяют Наблюдатель Риндлера как наблюдатель, который находится в состоянии покоя в координатах Риндлера, т.е. Икс, у, z и только варьируя т по прошествии времени. Координаты действительны в регионе ${ Displaystyle { scriptstyle 0 , <, X , <, infty, ; - X , <, T , <, X}}$ , который часто называют Клин риндлера, если ${ displaystyle alpha}$ представляет собственное ускорение (по гиперболе ${ displaystyle x = 1}$ ) наблюдателя Риндлера, собственное время которого определяется равным координатному времени Риндлера. Чтобы поддерживать эту мировую линию, наблюдатель должен ускоряться с постоянным надлежащим ускорением, при этом наблюдатели Риндлера находятся ближе к ${ displaystyle x = 0}$ (в Горизонт Риндлера ) с большим собственным ускорением. Все наблюдатели Риндлера мгновенно отдыхают во время ${ displaystyle T = 0}$ в инерциальной системе отсчета, и в это время наблюдатель Риндлера с надлежащим ускорением ${ displaystyle alpha _ {я}}$ будет на позиции ${ Displaystyle X = 1 / альфа _ {я}}$ (В самом деле ${ Displaystyle X = с ^ {2} / альфа _ {я}}$ , но мы предполагаем единицы, где ${ displaystyle c = 1}$ ), что также является постоянным расстоянием этого наблюдателя от горизонта Риндлера в координатах Риндлера. Если все наблюдатели Риндлера установят свои часы на ноль в ${ displaystyle T = 0}$ , то при определении системы координат Риндлера у нас есть выбор, из каких подходящее время будет равно координатному времени ${ displaystyle t}$ в координатах Риндлера, и собственное ускорение наблюдателя определяет значение ${ displaystyle alpha}$ выше (для других наблюдателей Риндлера, находящихся на разных расстояниях от горизонта Риндлера, координатное время будет равно некоторому постоянному кратному их собственному времени).^[18] Обычно систему координат Риндлера определяют так, чтобы наблюдатель Риндлера, чье собственное время совпадает с координатным временем, был тем, у кого надлежащее ускорение. ${ Displaystyle альфа = 1}$ , так что ${ displaystyle alpha}$ можно исключить из уравнений.

Приведенное выше уравнение было упрощено для ${ displaystyle c = 1}$ . Непростое уравнение более удобно для определения расстояния до горизонта Риндлера с учетом ускорения ${ displaystyle alpha}$ .

{ displaystyle { begin {align} t & = { frac {c} { alpha}} operatorname {arctanh} left ({ frac {cT} {X}} right) ; { overset {X , gg , cT} { приблизительно}} ; { frac {c ^ {2} T} { alpha X}} X & приблизительно { frac {c ^ {2} T} { альфа t}} ; { overset {T , приблизительно , t} { приблизительно}} ; { frac {c ^ {2}} { alpha}} end {align}}}

В оставшейся части статьи будет следовать соглашению о настройке как ${ Displaystyle альфа = 1}$ и ${ displaystyle c = 1}$ , поэтому единицы для ${ displaystyle X}$ и ${ displaystyle x}$ будет 1 единица ${ Displaystyle = с ^ {2} / альфа = 1}$ . Помните об этой настройке ${ Displaystyle альфа = 1}$ световая секунда в секунду² сильно отличается от настройки ${ Displaystyle альфа = 1}$ световой год / год². Даже если мы выберем единицы, где ${ displaystyle c = 1}$ , величина собственного ускорения ${ displaystyle alpha}$ будет зависеть от нашего выбора единиц измерения: например, если мы используем единицы световых лет для измерения расстояния, ( ${ displaystyle X}$ или же ${ displaystyle x}$ ) и годы на время, ( ${ displaystyle T}$ или же ${ displaystyle t}$ ), это означало бы ${ Displaystyle альфа = 1}$ световой год / год², равное примерно 9,5 м / с², а если мы будем использовать единицы световых секунд для измерения расстояния, ( ${ displaystyle X}$ или же ${ displaystyle x}$ ) и секунды для времени, ( ${ displaystyle T}$ или же ${ displaystyle t}$ ), это означало бы ${ Displaystyle альфа = 1}$ световая секунда в секунду², или 299 792 458 метров в секунду²).

Варианты формул преобразования

Дан более общий вывод формул преобразования, когда соответствующие Тетрада Ферми – Уокера формулируется, из которого Координаты Ферми или Правильные координаты можно вывести.^[19] В зависимости от выбора начала координат этих координат, можно получить метрику, замедление времени между временем в начале координат. ${ displaystyle dt_ {0}}$ и ${ displaystyle dt}$ в точке ${ displaystyle x}$ , а координата скорости света ${ displaystyle | dx | / | dt |}$ (это переменная скорость света не противоречит специальной теории относительности, потому что это всего лишь артефакт используемых ускоренных координат, в то время как в инерциальных координатах он остается постоянным). Вместо координат Ферми могут использоваться также радиолокационные координаты, которые получаются путем определения расстояния с помощью световых сигналов (см. Раздел Понятия расстояния ), по которой метрика, замедление времени и скорость света больше не зависят от координат - в частности, координатная скорость света остается идентичной скорости света ${ Displaystyle (с = 1)}$ в инерциальных системах отсчета:

{ displaystyle X}

в

{ displaystyle T = 0}

Преобразование, метрика, замедление времени и координатная скорость света

{ displaystyle X = 0}

Координаты Коттлера-Мёллера^{[H 12]}^[20]^[21]^[22]

{ displaystyle { begin {array} {c | c} { begin {align} T & = left (x + { frac {1} { alpha}} right) sinh ( alpha t) X & = left (x + { frac {1} { alpha}} right) cosh ( alpha t) - { frac {1} { alpha}} Y & = y Z & = z end {Выровнено}} & { begin {Выровнено} t & = { frac {1} { alpha}} operatorname {arctanh} left ({ frac {T} {X + { frac {1} { alpha} }}} right) x & = { sqrt { left (X + { frac {1} { alpha}} right) ^ {2} -T ^ {2}}} - { frac {1 } { alpha}} y & = Y z & = Z end {align}} end {array}}}

(2а)

{ displaystyle ds ^ {2} = - (1+ alpha x) {} ^ {2} dt ^ {2} + dx ^ {2} + dy ^ {2} + dz ^ {2}}

(2b)

{ displaystyle dt = (1+ alpha x) dt_ {0}, qquad { frac {| dx |} {| dt |}} = 1+ alpha x}

(2c)

Координаты Риндлера^[23]^[24]^[18]

{ displaystyle X = { frac {1} { alpha}}}

{ Displaystyle { begin {array} {c | c} { begin {align} T & = x sinh ( alpha t) X & = x cosh ( alpha t) Y & = y Z & = z end {align}} & { begin {align} t & = { frac {1} { alpha}} operatorname {arctanh} { frac {T} {X}} x & = { sqrt {X ^ {2} -T ^ {2}}} y & = Y z & = Z end {выравнивается}} end {array}}}

(2d)

{ displaystyle ds ^ {2} = - ( alpha x) ^ {2} dt ^ {2} + dx ^ {2} + dy ^ {2} + dz ^ {2}}

(2e)

{ displaystyle dt = alpha x dt_ {0}, qquad { frac {| dx |} {| dt |}} = alpha x}

(2f)

Координаты радара (координаты Ласса)^[25]^[26]^[8]^[9]

{ displaystyle X = { frac {1} { alpha}}}

{ displaystyle { begin {array} {c | c} { begin {align} T & = { frac {1} { alpha}} e ^ { alpha x} sinh ( alpha t) X & = { frac {1} { alpha}} e ^ { alpha x} cosh ( alpha t) Y & = y Z & = z end {align}} & { begin {align} t & = { frac {1} { alpha}} operatorname {arctanh} { frac {T} {X}} x & = { frac {1} {2 alpha}} ln left [ alpha {} ^ {2} left (X ^ {2} -T ^ {2} right) right] y & = Y z & = Z end {выровнено}} end {array}}}

(2 г)

{ displaystyle ds ^ {2} = e ^ {2 alpha x} left (-dt ^ {2} + dx ^ {2} right) + dy ^ {2} + dz ^ {2}}

(2ч)

{ displaystyle dt = e ^ { alpha x} dt_ {0}, qquad { frac {| dx |} {| dt |}} = 1}

(2i)

Наблюдатели Риндлера

В новом графике (1а) с ${ displaystyle c = 1}$ и ${ Displaystyle альфа = 1}$ , естественно взять поле coframe

{ displaystyle d sigma ^ {0} = x , dt, ; ; d sigma ^ {1} = dx, ; ; d sigma ^ {2} = dy, ; ; d сигма ^ {3} = dz}

который имеет двойную поле кадра

{ displaystyle { vec {e}} _ {0} = { frac {1} {x}} partial _ {t}, ; ; { vec {e}} _ {1} = partial _ {x}, ; ; { vec {e}} _ {2} = partial _ {y}, ; ; { vec {e}} _ {3} = partial _ {z} }

Это определяет местная рамка Лоренца в касательное пространство на каждом мероприятие (в области, охватываемой нашей диаграммой Риндлера, а именно в области клина Риндлера). В интегральные кривые из подобный времени единичное векторное поле ${ displaystyle scriptstyle { vec {e}} _ {0}}$ дать подобие времени, состоящий из мировых линий семейства наблюдателей, называемых Наблюдатели Риндлера. На диаграмме Риндлера эти мировые линии отображаются как вертикальные координатные линии. ${ displaystyle scriptstyle x ; = ; x_ {0}, ; y ; = ; y_ {0}, ; z ; = ; z_ {0}}$ . Используя преобразование координат выше, мы обнаруживаем, что они соответствуют гиперболическим дугам в исходной декартовой карте.

Некоторые типичные наблюдатели Риндлера (темно-синие гиперболические дуги) изображены с помощью декартовой карты. Красные линии под углом 45 градусов от вертикали представляют горизонт Риндлера; система координат Риндлера определяется только справа от этой границы.

Как и в случае любой времениподобной конгруэнции в любом лоренцевом многообразии, это сравнение имеет кинематическое разложение (видеть Уравнение райчаудхури ). В этом случае расширение и завихренность совпадения наблюдателей Риндлера исчезнуть. Из исчезновения тензора разложения следует, что каждый из наших наблюдателей сохраняет постоянное расстояние до своих соседей. Исчезновение тензора завихренности означает, что мировые линии наших наблюдателей не скручиваются друг относительно друга; это своего рода локальное отсутствие «закрутки».

В вектор ускорения каждого наблюдателя задается ковариантная производная

{ displaystyle nabla _ {{ vec {e}} _ {0}} { vec {e}} _ {0} = { frac {1} {x}} { vec {e}} _ { 1}}

То есть каждый наблюдатель Риндлера ускоряется в ${ displaystyle scriptstyle partial _ {x}}$ направление. По отдельности, каждый наблюдатель на самом деле ускоряется с постоянная величина в этом направлении, поэтому их мировые линии являются лоренцевыми аналогами окружностей, которые являются кривыми постоянной кривизны пути в евклидовой геометрии.

Поскольку наблюдатели Риндлера без завихренности, Они также гиперповерхность ортогональная. Ортогональные пространственные гиперпространства имеют вид ${ Displaystyle scriptstyle т ; = ; t_ {0}}$ ; они выглядят как горизонтальные полуплоскости на диаграмме Риндлера и как полуплоскости через ${ Displaystyle scriptstyle T ; = ; X ; = ; 0}$ в декартовой диаграмме (см. рисунок выше). Параметр ${ Displaystyle scriptstyle dt ; = ; 0}$ в линейном элементе мы видим, что они имеют обычную евклидову геометрию, ${ Displaystyle scriptstyle d sigma ^ {2} ; = ; dx ^ {2} , + , dy ^ {2} , + , dz ^ {2}, ; forall x , > , 0, ; forall y, , z}$ . Таким образом, пространственные координаты на карте Риндлера имеют очень простую интерпретацию, согласующуюся с утверждением, что наблюдатели Риндлера взаимно стационарны. Мы вернемся к этому свойству жесткости наблюдателей Риндлера чуть позже в этой статье.

«Парадоксальное» свойство

Обратите внимание, что наблюдатели Риндлера с меньшей постоянной координатой x ускоряются. Сильнее поддерживать. Это может показаться удивительным, потому что в ньютоновской физике наблюдатели, поддерживающие постоянное относительное расстояние, должны разделять одно и тоже ускорение. Но в релятивистской физике мы видим, что задний конец стержня, который ускоряется некоторой внешней силой (параллельной его оси симметрии), должен ускоряться немного сильнее, чем ведущий конец, иначе он должен в конечном итоге сломаться. Это проявление Лоренцево сокращение. По мере ускорения стержня его скорость увеличивается, а длина уменьшается. Поскольку он становится короче, задняя часть должна ускоряться сильнее, чем передняя. Другой способ взглянуть на это: серверная часть должна достичь такого же изменения скорости за более короткий период времени. Это приводит к дифференциальному уравнению, показывающему, что на некотором расстоянии ускорение заднего конца расходится, в результате чего Горизонт Риндлера.

Это явление лежит в основе известного «парадокса», Парадокс космического корабля Белла. Однако это простое следствие релятивистской кинематики. Один из способов увидеть это - заметить, что величина вектора ускорения - это просто кривизна пути соответствующей мировой линии. Но мировые линии наших наблюдателей Риндлера являются аналогами семейства концентрических окружностей в евклидовой плоскости, поэтому мы просто имеем дело с лоренцевым аналогом факта, известного конькобежцам: в семье концентрических кругов внутренние круги должны изгибаться быстрее (на единицу длины дуги), чем внешние.

Минковский наблюдатели

Типичный наблюдатель Минковского (темно-синяя гиперболическая секущая кривая), изображенный с помощью диаграммы Риндлера. Горизонт Риндлера показан красным.

Стоит также ввести альтернативный фрейм, заданный в диаграмме Минковского естественным выбором

{ displaystyle { vec {f}} _ {0} = partial _ {T}, ; { vec {f}} _ {1} = partial _ {X}, ; { vec {f }} _ {2} = partial _ {Y}, ; { vec {f}} _ {3} = partial _ {Z}}

Преобразуя эти векторные поля с помощью преобразования координат, приведенного выше, мы обнаруживаем, что на диаграмме Риндлера (в клине Риндлера) этот кадр становится

{ displaystyle { begin {align} { vec {f}} _ {0} & = { frac {1} {x}} cosh (t) , partial _ {t} - sinh (t ) , partial _ {x} { vec {f}} _ {1} & = - { frac {1} {x}} sinh (t) , partial _ {t} + cosh (t) , partial _ {x} { vec {f}} _ {2} & = partial _ {y}, ; { vec {f}} _ {3} = partial _ {z} end {выровнен}}}

Вычисление кинематического разложения времениподобного сравнения, определенного времяподобным единичным векторным полем ${ displaystyle scriptstyle { vec {f}} _ {0}}$ , находим, что расширение и завихренность снова исчезают, и, кроме того, обращается в нуль вектор ускорения: ${ displaystyle scriptstyle nabla _ { vec {f}} _ {0}} { vec {f}} _ {0} ; = ; 0}$ . Другими словами, это геодезическая конгруэнтность; соответствующие наблюдатели находятся в состоянии инерционное движение. В исходной декартовой карте эти наблюдатели, которых мы назовем Минковский наблюдатели, находятся в покое.

На карте Риндлера мировые линии наблюдателей Минковского выглядят как гиперболические секущие кривые, асимптотические относительно координатной плоскости. ${ Displaystyle scriptstyle х ; = ; 0}$ . В частности, в координатах Риндлера мировая линия наблюдателя Минковского, проходящего через событие ${ displaystyle scriptstyle t ; = ; t_ {0}, ; x ; = ; x_ {0}, ; y ; = ; y_ {0}, ; z ; = ; z_ {0}}$ является

{ displaystyle { begin {align} t & = operatorname {arctanh} left ({ frac {s} {x_ {0}}} right), ; - x_ {0}

куда ${ displaystyle scriptstyle s}$ - подходящее время для этого наблюдателя Минковского. Обратите внимание, что только небольшая часть его истории покрыта диаграммой Риндлера. Это ясно показывает, почему диаграмма Риндлера нет геодезически полный; времяподобные геодезические бегут за пределы области, охватываемой картой, за конечное собственное время. Конечно, мы уже знали, что карта Риндлера не может быть геодезически полной, потому что она покрывает только часть исходной декартовой карты, которая является геодезически полная карта.

В случае, изображенном на рисунке, ${ Displaystyle scriptstyle x_ {0} ; = ; 1}$ и мы нарисовали (правильно масштабировали и увеличили) световые конусы на ${ displaystyle scriptstyle s , in , left {- { frac {1} {2}}, ; 0, ; { frac {1} {2}} right }}$ .

Горизонт Риндлера

На координатной диаграмме Риндлера есть координатная особенность в Икс = 0, где метрический тензор (выраженный в координатах Риндлера) обращается в нуль детерминант. Это происходит потому, что как Икс → 0 ускорение наблюдателей Риндлера расходится. Как видно из рисунка, иллюстрирующего клин Риндлера, локус Икс = 0 на диаграмме Риндлера соответствует локусу Т² = Икс², Икс > 0 в декартовой карте, которая состоит из двух нулевых полуплоскостей, каждая из которых управляется нулевой геодезической конгруэнцией.
На данный момент мы просто рассматриваем горизонт Риндлера как границу координат Риндлера. Если мы рассмотрим набор ускоряющихся наблюдателей, которые имеют постоянное положение в координатах Риндлера, ни один из них никогда не сможет получить световые сигналы от событий с Т ≥ Икс (на диаграмме это будут события слева от строки Т = Икс вдоль которого лежит верхний красный горизонт; однако эти наблюдатели могли получать сигналы от событий с Т ≥ Икс если бы они остановили свое ускорение и сами пересекли эту линию), они также не могли бы послать сигналы событиям с Т ≤ −Икс (события в строке или слева от нее Т = −Икс вдоль которого лежит нижний красный горизонт; эти события лежат за пределами всего будущего световые конусы их прошлой мировой линии).Кроме того, если мы рассмотрим членов этого набора ускоряющихся наблюдателей все ближе и ближе к горизонту, в пределе, когда расстояние до горизонта приближается к нулю, постоянное собственное ускорение, испытываемое наблюдателем на этом расстоянии (которое также будет G- сила, испытываемая таким наблюдателем) приблизилась бы к бесконечности. Оба этих факта также были бы правдой, если бы мы рассматривали группу наблюдателей, парящих вне горизонт событий из черная дыра, каждый наблюдатель парит с постоянным радиусом в Координаты Шварцшильда. Фактически, в непосредственной близости от черной дыры геометрия, близкая к горизонту событий, может быть описана в координатах Риндлера. Излучение Хокинга в случае ускоряющейся системы отсчета называется Унру радиация. Связь - это эквивалент ускорения гравитации.
Геодезические

Уравнения геодезических в карте Риндлера легко получаются из геодезических Лагранжиан; они есть
${ displaystyle { ddot {t}} + { frac {2} {x}} , { dot {x}} , { dot {t}} = 0, ; { ddot {x} } + x , { dot {t}} ^ {2} = 0, ; { ddot {y}} = 0, ; { ddot {z}} = 0}$
Конечно, в исходной декартовой карте геодезические отображаются в виде прямых линий, поэтому мы могли легко получить их на карте Риндлера, используя наше преобразование координат. Однако полезно получить и изучить их независимо от исходной карты, и мы сделаем это в этом разделе.

Некоторые репрезентативные нулевые геодезические (черные гиперболические полукруглые дуги) проецируются в пространственный гиперсрез t = 0 наблюдателей Риндлера. Горизонт Риндлера показан в виде плоскости пурпурного цвета.
Из первого, третьего и четвертого сразу получаем первые интегралы
${ displaystyle { dot {t}} = { frac {E} {x ^ {2}}}, ; ; { dot {y}} = P, ; ; { dot {z} } = Q}$
Но из линейного элемента у нас есть ${ displaystyle scriptstyle epsilon ; = ; - x ^ {2} , { dot {t}} ^ {2} , + , { dot {x}} ^ {2} , + , { dot {y}} ^ {2} , + , { dot {z}} ^ {2}}$ куда ${ Displaystyle scriptstyle epsilon ; in ; left {- 1, , 0, , 1 right }}$ для времениподобных, нулевых и пространственноподобных геодезических соответственно. Это дает четвертый первый интеграл, а именно
${ displaystyle { dot {x}} ^ {2} = left ( epsilon + { frac {E ^ {2}} {x ^ {2}}} right) -P ^ {2} -Q ^ {2}}$ .
Этого достаточно, чтобы дать полное решение уравнений геодезических.
В случае нулевые геодезические, из ${ displaystyle scriptstyle { frac {E ^ {2}} {x ^ {2}}} , - , P ^ {2} , - , Q ^ {2}}$ с ненулевым ${ displaystyle scriptstyle E}$ , мы видим, что координата x пробегает интервал ${ displaystyle scriptstyle 0 , <, x , <, { frac {E} { sqrt {P ^ {2} , + , Q ^ {2}}}}}$ .
Полное семейство из семи параметров, дающее любую нулевую геодезическую через любое событие в клине Риндлера, является
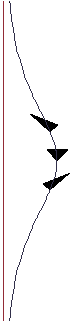
${ displaystyle { begin {align} t-t_ {0} & = operatorname {arctanh} left ({ frac {1} {E}} left [s left (P ^ {2} + Q ^ {2} right) - { sqrt {E ^ {2} - left (P ^ {2} + Q ^ {2} right) x_ {0} ^ {2}}} right] right) + & quad quad operatorname {arctanh} left ({ frac {1} {E}} { sqrt {E ^ {2} - (P ^ {2} + Q ^ {2}) x_ {0} ^ {2}}} right) x & = { sqrt {x_ {0} ^ {2} + 2s { sqrt {E ^ {2} - (P ^ {2} + Q ^ { 2}) x_ {0} ^ {2}}} - s ^ {2} (P ^ {2} + Q ^ {2})}} y-y_ {0} & = Ps; ; ; z-z_ {0} = Qs end {выровнено}}}$
Построение треки некоторых репрезентативных нулевых геодезических через данное событие (то есть проецирование на гиперсрез ${ Displaystyle scriptstyle т , = , 0}$ ), мы получаем картину, которая подозрительно похожа на семейство всех полукругов, проходящих через точку и ортогональных горизонту Риндлера. (Смотрите рисунок.)
Метрика Ферма

Тот факт, что в диаграмме Риндлера проекции нулевых геодезических на любой пространственный гиперсрез для наблюдателей Риндлера представляют собой просто полукруглые дуги, можно проверить непосредственно из только что данного общего решения, но есть очень простой способ увидеть это. А статическое пространство-время тот, в котором времяподобный Вектор убийства поле можно найти. В этом случае у нас есть однозначно определенное семейство (идентичных) пространственных гиперпространств, ортогональных соответствующим статическим наблюдателям (которым не обязательно быть инерциальными наблюдателями). Это позволяет нам определить новую метрику на любом из этих гиперсрезов, которая конформно связана с исходной метрикой, унаследованной от пространства-времени, но с тем свойством, что геодезические в новой метрике Риманова метрика на трехмерном римановом многообразии) - это в точности проекции нулевых геодезических пространства-времени. Эта новая метрика называется Метрика Ферма, и в статическом пространстве-времени, снабженном координатной диаграммой, в которой линейный элемент имеет форму
${ Displaystyle ds ^ {2} = g_ {00} , dt ^ {2} + g_ {jk} , dx ^ {j} , dx ^ {k}, ; ; j, ; k в {1,2,3 }}$
метрика Ферма на ${ Displaystyle scriptstyle т ; = ; 0}$ просто
${ displaystyle d rho ^ {2} = { frac {1} {- g_ {00}}} left (g_ {jk} , dx ^ {j} , dx ^ {k} right)}$
(где подразумевается, что метрические коэффициенты оцениваются при ${ Displaystyle scriptstyle т ; = ; 0}$ ).
В диаграмме Риндлера времяподобный перевод ${ displaystyle scriptstyle partial _ {t}}$ такое векторное поле Киллинга, так что это статическое пространство-время (неудивительно, поскольку пространство-время Минковского, конечно, тривиально является статическим вакуумным решением задачи Уравнение поля Эйнштейна ). Поэтому мы можем сразу записать метрику Ферма для наблюдателей Риндлера:
${ displaystyle d rho ^ {2} = { frac {1} {x ^ {2}}} left (dx ^ {2} + dy ^ {2} + dz ^ {2} right), ; ; forall x> 0, ; ; forall y, z}$
Но это всем известный линейный элемент гиперболическое трехмерное пространство ЧАС³ в диаграмма верхнего полупространства. Это очень похоже на хорошо известный диаграмма верхней полуплоскости для гиперболической плоскости ЧАС², знакомый поколениям комплексный анализ студенты в связи с проблемы конформного отображения (и многое другое), и многие математически мыслящие читатели уже знают, что геодезические ЧАС² в модели верхней полуплоскости - это просто полукруги (ортогональные бесконечно удаленной окружности, представленной действительной осью).
Симметрии

Поскольку диаграмма Риндлера является координатной диаграммой пространства-времени Минковского, мы ожидаем найти десять линейно независимых векторных полей Киллинга. Действительно, в декартовой карте мы легко можем найти десять линейно независимых векторных полей Киллинга, порождающих соответственно подгруппы с одним параметром перевод времени, три пространственных, три вращения и три повышения. Вместе они порождают (собственно изохронную) группу Пуанкаре, группу симметрии пространства-времени Минковского.
Однако поучительно записывать и решать векторные уравнения Киллинга напрямую. Мы получаем четыре знакомых вида векторных поля Киллинга
${ Displaystyle partial _ {t}, ; ; partial _ {y}, ; ; partial _ {z}, ; ; - z , partial _ {y} + y , partial _ {z}}$
(перевод во времени, пространственные переводы, ортогональные направлению ускорения, и пространственное вращение, ортогональное направлению ускорения) плюс еще шесть:
${ Displaystyle { begin {align} & exp ( pm t) , left ({ frac {y} {x}} , partial _ {t} pm left [y , partial _ {x} -x , partial _ {y} right] right) & exp ( pm t) , left ({ frac {z} {x}} , partial _ {t} pm left [z , partial _ {x} -x , partial _ {z} right] right) & exp ( pm t) , left ({ frac {1} {x}} , partial _ {t} pm partial _ {x} right) end {выравнивается}}}$
(где знаки выбраны последовательно + или -). Мы оставляем это как упражнение, чтобы выяснить, как они связаны со стандартными генераторами; здесь мы хотим указать, что мы должны иметь возможность получить генераторы, эквивалентные ${ Displaystyle scriptstyle partial _ {T}}$ в декартовой карте, однако клин Риндлера, очевидно, не инвариантен относительно этого перевода. Как это может быть? Ответ заключается в том, что, как и все, что определяется системой дифференциальных уравнений в частных производных на гладком многообразии, уравнение Киллинга, как правило, имеет локально определенные решения, но они могут не существовать глобально. То есть, с подходящими ограничениями на параметр группы, поток убийства всегда может быть определен в подходящем местный район, но поток может быть нечетко определен глобально. Это не имеет ничего общего с лоренцевыми многообразиями как таковыми, поскольку та же проблема возникает при изучении общих гладкие многообразия.
Понятия расстояния

Один из многих ценных уроков, которые можно извлечь из изучения диаграммы Риндлера, заключается в том, что на самом деле существует несколько отчетливый (но разумные) представления о расстояние которые могут использоваться наблюдателями Риндлера.

Оперативное значение радар расстояние между двумя наблюдателями Риндлера (темно-синие вертикальные линии). Горизонт Риндлера показан слева (красная вертикальная линия). Мировая линия радиолокационного импульса также изображена вместе с (правильно масштабированными) световыми конусами в событиях A, B, C.
Первая - та, которую мы негласно использовали выше: индуцированная риманова метрика на пространственных гиперпространствах. ${ Displaystyle scriptstyle т ; = ; t_ {0}}$ . Мы назовем это линейка расстояние поскольку он соответствует этой индуцированной римановой метрике, но его рабочий смысл может быть не сразу очевиден.
С точки зрения физических измерений более естественным понятием расстояния между двумя мировыми линиями является радар расстояние. Это вычисляется путем отправки нулевой геодезической от мировой линии нашего наблюдателя (событие A) к мировой линии некоторого небольшого объекта, после чего он отражается (событие B) и возвращается к наблюдателю (событие C). Радиолокационное расстояние затем получается путем деления времени путешествия туда и обратно, измеренного идеальными часами, которые несет наш наблюдатель.
(В пространстве-времени Минковского, к счастью, мы можем игнорировать возможность множественных нулевых геодезических путей между двумя мировыми линиями, но в космологических моделях и других приложениях^{[который? ]} все не так просто. Мы также должны предостеречь от предположения, что это понятие расстояния между двумя наблюдателями дает понятие, которое является симметричным относительно смены наблюдателей.)
В частности, рассмотрим пару наблюдателей Риндлера с координатами ${ displaystyle scriptstyle x ; = ; x_ {0}, ; y ; = ; 0, ; z ; = ; 0}$ и ${ Displaystyle scriptstyle х ; = ; x_ {0} , + , h, ; y ; = ; 0, ; ; z ; = ; 0}$ соответственно. (Обратите внимание, что первый из них, следящий наблюдатель, ускоряется немного сильнее, чтобы не отставать от ведущего наблюдателя). Параметр ${ Displaystyle scriptstyle dy ; = ; dz ; = ; 0}$ в элементе линии Риндлера мы легко получаем уравнение нулевых геодезических, движущихся в направлении ускорения:
${ displaystyle t-t_ {0} = log left ({ frac {x} {x_ {0}}} right)}$
Следовательно, радарное расстояние между этими двумя наблюдателями определяется как
${ displaystyle x_ {0} , log left (1 + { frac {h} {x_ {0}}} right) = h - { frac {h ^ {2}} {2 , x_ {0}}} + O left (h ^ {3} right)}$
Это немного меньше, чем расстояние линейки, но для ближайших наблюдателей расхождение незначительно.
Третье возможное понятие расстояния таково: наш наблюдатель измеряет расстояние угол подчиняется единичному диску, помещенному на некоторый объект (не точечный объект), как это видно из его местоположения. Мы называем это расстояние оптического диаметра. Из-за простого характера нулевых геодезических в пространстве-времени Минковского мы можем легко определить оптическое расстояние между нашей парой наблюдателей Риндлера (выровненное по направлению ускорения). На эскизе должно быть правдоподобно, что расстояние оптического диаметра масштабируется как ${ displaystyle scriptstyle h , + , { frac {1} {x_ {0}}} , + , O left (h ^ {3} right)}$ . Следовательно, в случае следящего наблюдателя, оценивающего расстояние до ведущего наблюдателя (случай ${ Displaystyle scriptstyle ч ,> , 0}$ ) оптическое расстояние немного больше расстояния линейки, которое немного больше расстояния радара. Читателю следует уделить время рассмотрению случая, когда ведущий наблюдатель оценивает расстояние до следящего наблюдателя.
Существуют и другие понятия расстояния, но суть ясна: хотя значения этих различных понятий в целом не совпадают для данной пары наблюдателей Риндлера, все они согласны с тем, что каждая пара наблюдателей Риндлера поддерживает постоянное расстояние. Дело в том, что очень близко Наблюдатели Риндлера взаимно стационарны, это следует из отмеченного выше факта, что тензор разложения сравнения Риндлера тождественно равен нулю. Однако мы показали здесь, что в различных смыслах это свойство жесткости сохраняется и в больших масштабах. Это действительно замечательное свойство жесткости с учетом хорошо известного факта, что в релятивистской физике никакая штанга не может быть жестко ускорена (и ни один диск нельзя раскрутить жестко) - по крайней мере, не без неоднородных напряжений. Самый простой способ увидеть это - заметить, что в ньютоновской физике, если мы «пинаем» твердое тело, все элементы материи в теле немедленно изменяют свое состояние движения. Это, конечно, несовместимо с релятивистским принципом, согласно которому никакая информация, имеющая какой-либо физический эффект, не может передаваться быстрее скорости света.
Отсюда следует, что если стержень ускоряется некоторой внешней силой, приложенной в любом месте по его длине, элементы материи в различных различных местах стержня не могут все ощущать одинаковую величину ускорения, если стержень не должен расширяться без ограничений и в конечном итоге ломаться. Другими словами, ускоренный стержень, который не ломается, должен выдерживать напряжения, изменяющиеся по длине. Более того, в любом мысленном эксперименте с меняющимися во времени силами, независимо от того, «пинаем» мы объект или пытаемся его постепенно ускорять, мы не можем избежать проблемы избегания механических моделей, несовместимых с релятивистской кинематикой (потому что отдаленные части тела реагируют слишком быстро к приложенной силе).
Возвращаясь к вопросу о практическом значении расстояния линейки, мы видим, что это должно быть расстояние, которое наши наблюдатели получат, если они очень медленно переходят из руки в руку маленькую линейку, которую постоянно ставят встык. Но для подробного обоснования этой интерпретации потребуется некая материальная модель.
Обобщение на искривленные пространства-времени

Координаты Риндлера, как описано выше, могут быть обобщены на искривленное пространство-время, как Нормальные координаты Ферми. Существенное обобщение заключается в построении подходящей ортонормированной тетрады и последующей ее транспортировке по заданной траектории с помощью Ферми – Уокер транспорт правило. Подробнее см. Статью Ни и Циммерманн в приведенных ниже ссылках. Такое обобщение фактически позволяет изучать инерционные и гравитационные эффекты в лаборатории на Земле, а также более интересные связанные инерционно-гравитационные эффекты.
История

Обзор
Координаты Коттлера – Мёллера и Риндлера
Альберт Эйнштейн (1907)^{[H 13]} изучили эффекты в равномерно ускоренной системе отсчета, получив уравнения для координатно-зависимых замедление времени и скорость света эквивалентно (2c), а чтобы сделать формулы независимыми от источника наблюдателя, он получил замедление времени (2i) в формальном согласии с координатами радара. Представляя концепцию Родилась жесткость, Макс Борн (1909)^{[H 14]} отметил, что формулы для гиперболического движения могут использоваться как преобразования в «гиперболически ускоренную систему отсчета» (Немецкий: hyperbolisch beschleunigtes Bezugsystem) эквивалентно (2d). Работа Борна была развита далее Арнольд Зоммерфельд (1910)^{[H 15]} и Макс фон Лауэ (1911)^{[H 16]} которые оба получили (2d) с помощью воображаемый числа, которые были суммированы Вольфганг Паули (1921)^[16] кто кроме координат (2d) также получил метрику (2e) с использованием мнимых чисел. Эйнштейн (1912)^{[H 17]} изучили статическое гравитационное поле и получили метрику Коттлера-Мёллера (2b), а также приближения к формулам (2а) с использованием координатно-зависимой скорости света.^[27] Хендрик Лоренц (1913)^{[H 18]} получили координаты, аналогичные (2d, 2e, 2f) при изучении Эйнштейна принцип эквивалентности и однородное гравитационное поле.
Подробное описание было дано Фридрих Коттлер (1914),^{[H 19]} кто сформулировал соответствующий ортонормированный тетрада, формулы преобразования и метрика (2а, 2b). Также Карл Боллерт (1922)^{[H 20]} получили метрику (2b) в своем исследовании равномерного ускорения и однородных гравитационных полей. В статье, посвященной жесткости Борна, Жорж Лемэтр (1924)^{[H 21]} полученные координаты и метрика (2а, 2b). Альберт Эйнштейн и Натан Розен (1935) описал (2d, 2e) как «известные» выражения для однородного гравитационного поля.^{[H 22]} После Кристиан Мёллер (1943)^{[H 11]} полученный (2а, 2b) в качестве исследования, связанного с однородными гравитационными полями, он (1952 г.)^{[H 23]} а также Мизнер и Торн и Уиллер (1973)^[2] использовал Ферми – Уокер транспорт чтобы получить те же уравнения.
Хотя эти исследования касались плоского пространства-времени, Вольфганг Риндлер (1960)^[14] проанализировал гиперболическое движение в искривленном пространстве-времени и показал (1966)^[15] аналогия между гиперболическими координатами (2d, 2e) в плоском пространстве-времени с Крускал координаты в Пространство Шварцшильда. Это повлияло на последующих авторов в их формулировании Унру радиация измеряется наблюдателем в гиперболическом движении, что аналогично описанию Радиация Хокинга из черные дыры.
Горизонт
Борн (1909) показал, что внутренние точки твердого тела Борна при гиперболическом движении могут находиться только в области ${ Displaystyle X / влево (X ^ {2} -T ^ {2} right)> 0}$ .^{[H 24]} Зоммерфельд (1910) определил, что координаты, допускаемые для преобразования между инерциальными и гиперболическими координатами, должны удовлетворять ${ displaystyle T$ .^{[H 25]} Коттлер (1914)^{[H 26]} определил этот регион как ${ displaystyle X ^ {2} -T ^ {2}> 0}$ , и указал на существование «пограничной плоскости» (Немецкий: Гренцебене) ${ displaystyle c ^ {2} / alpha + x}$ , за пределами которого никакой сигнал не может достичь наблюдателя в гиперболическом движении. Это называлось «горизонтом наблюдателя» (Немецкий: Horizont des Beobachters) Боллерта (1922).^{[H 27]} Риндлер (1966)^[15] продемонстрировал связь между таким горизонтом и горизонтом в координатах Крускала.
Координаты радара
Используя формализм Боллерта, Степан Мохорович (1922)^{[H 28]} сделали другой выбор некоторого параметра и получили метрику (2ч) с ошибкой печати, которая была исправлена Боллертом (1922b) с помощью другой ошибки печати, пока версия без ошибки печати не была предоставлена Мохоровичичем (1923). Кроме того, Мохорович ошибочно утверждал, что метрика (2b, теперь называемая метрикой Коттлера-Мёллера) неверна, что было опровергнуто Боллером (1922).^{[H 29]} Метрическая (2ч) был заново открыт Гарри Ласс (1963),^[13] который также дал соответствующие координаты (2 г), которые иногда называют «координатами девушки».^[9] Метрическая (2ч), а также (2а, 2b), также был получен Фриц Рорлих (1963).^[12] В конце концов, координаты Ласса (2 г, 2ч) были отождествлены с радиолокационными координатами Desloge & Philpott (1987).^[28]^[8]
Таблица с историческими формулами
Эйнштейн (1907)^{[H 30]}
${ Displaystyle { scriptstyle { begin {matrix} sigma = tau left (1 + { frac { gamma xi} {c ^ {2}}} right) sigma = tau e ^ { gamma xi / c ^ {2}} c left (1 + { frac { gamma xi} {c ^ {2}}} right) end {matrix}}}}$
Родился (1909 г.)^{[H 14]}
${ Displaystyle { scriptstyle { begin {matrix} x = -q xi, y = eta, z = zeta, t = { frac {p} {c ^ {2}}} xi left (p = x _ { tau}, q = -t _ { tau} = { sqrt {1 + p ^ {2} / c ^ {2}}} right) { boldsymbol { downarrow}} x ^ {2} -c ^ {2} t ^ {2} = xi ^ {2} end {matrix}}}}$
Герглотц (1909)^{[H 31]}^[29]
${ displaystyle { scriptstyle { begin {matrix} { begin {align} x & = x ' y & = y' t-z & = (t'-z ') e ^ { vartheta} t + z & = (t '+ z') e ^ {- vartheta} end {выравнивается}} { boldsymbol { downarrow}} x = x_ {0}, quad y = y_ {0} , quad z = { sqrt {z_ {0} ^ {2} + t ^ {2}}} end {matrix}}}}$
Зоммерфельд (1910)^{[H 15]}
${ Displaystyle scriptstyle { begin {align} x & = r cos varphi y & = y ' z & = z' l & = r sin varphi varphi & = i psi, l = ict end {выровнено}}}$
фон Лауэ (1911)^{[H 32]}
${ Displaystyle scriptstyle { begin {выровнено} X & = R cos varphi L & = R sin varphi R ^ {2} & = X ^ {2} + L ^ {2} загар varphi & = { frac {L} {X}} end {align}}}$
Эйнштейн (1912)^{[H 17]}
${ displaystyle { scriptstyle { begin {matrix} d xi ^ {2} -d tau ^ {2} = dx ^ {2} -c ^ {2} dt ^ {2} { boldsymbol { downarrow}} c = c_ {0} + ax { boldsymbol { downarrow}} { begin {align} xi & = x + { frac {ac} {2}} t ^ { 2} eta & = y zeta & = z tau & = ct end {align}} end {matrix}}}}$
Коттлер (1912)^{[H 33]}
${ displaystyle { scriptstyle { begin {align} x ^ {(1)} & = x_ {0} ^ {(1)} x ^ {(2)} & = x_ {0} ^ {(2 )} x ^ {(3)} & = b cos i varphi x ^ {(4)} & = b sin i varphi end {align}}}}$
Лоренц (1913)^{[H 18]}
${ displaystyle { scriptstyle { begin {matrix} dc = { frac {g} {c}} dz hline { begin {align} z & = a left (z'-z_ {0} ^ { prime} right) ct & = b left (z'-z_ {0} ^ { prime} right) a & = { frac {1} {2}} left (e ^ {kt '} + e ^ {- kt} right) b & = { frac {1} {2}} left (e ^ {kt'} - e ^ {- kt} right) end {выравнивается} } { boldsymbol { downarrow}} c '= k left (z'-z_ {0} ^ { prime} right), z'-z_ {0} ^ { prime} = { frac {c ^ {2}} {g}} { boldsymbol { downarrow}} { begin {align} & dx ^ {2} + dy ^ {2} + dz ^ {2} - c ^ {2} dt & = dx ^ { prime 2} + dy ^ { prime 2} + dz ^ { prime 2} -c ^ { prime 2} dt ^ { prime 2} end {выровнено}} end {matrix}}}}$
Коттлер (1914a)^{[H 34]}
${ displaystyle { scriptstyle { begin {matrix} { begin {align} x ^ {(1)} & = x_ {0} ^ {(1)} x ^ {(2)} & = x_ { 0} ^ {(2)} x ^ {(3)} & = b cos iu x ^ {(4)} & = b sin iu end {align}} { boldsymbol { downarrow}} ds ^ {2} = - c ^ {2} d tau ^ {2} = b ^ {2} (du) ^ {2} { boldsymbol { downarrow}} { begin {matrix} c_ {1} ^ {(1)} = 0, && c_ {1} ^ {(2)} = 0, && c_ {1} ^ {(3)} = - sin iu, && c_ { 1} ^ {(4)} = cos iu, c_ {2} ^ {(1)} = 0, && c_ {2} ^ {(2)} = 0, && c_ {2} ^ {(3) } = - cos iu, && c_ {2} ^ {(4)} = - sin iu, end {matrix}} { boldsymbol { downarrow}} dS ^ {2} = (dX ' ) ^ {2} + (dY ') ^ {2} + (dZ') ^ {2} - left (c + { frac {Z'c} {b}} right) ^ {2} dT ' { boldsymbol { downarrow}} c '= c + { frac {Z'c ^ {2}} {b}} cdot { frac {1} {c}} end {matrix}}} }$
Коттлер (1914b)^{[H 35]}
${ displaystyle scriptstyle { begin {matrix} { begin {matrix} c_ {1} ^ {(1)} = 0, && c_ {1} ^ {(2)} = 0, && c_ {1} ^ {( 3)} = { frac {1} {i}} sinh u, && c_ {1} ^ {(4)} = ch u, c_ {2} ^ {(1)} = 0, && c_ { 2} ^ {(2)} = 0, && c_ {2} ^ {(3)} = { frac {1} {i}} ch u, && c_ {2} ^ {(4)} = - sinh u, c_ {3} ^ {(1)} = 1, && c_ {3} ^ {(2)} = 0, && c_ {3} ^ {(3)} = 0, && c_ {3} ^ {( 4)} = 0, c_ {4} ^ {(1)} = 0, && c_ {4} ^ {(2)} = 1, && c_ {4} ^ {(3)} = 0, && c_ {4 } ^ {(4)} = 0, end {matrix}} { boldsymbol { downarrow}} X = x + Delta ^ {(2)} c_ {2} + Delta ^ {(3 )} c_ {3} + Delta ^ {(4)} c_ {4} { boldsymbol { downarrow}} { begin {align} X & = x_ {0} + { mathfrak {X} } ' Y & = y_ {0} + { mathfrak {Y}}' Z & = left (b + { mathfrak {Z}} ' right) cosh { mathfrak {u}} cT & = left (b + { mathfrak {Z}} ' right) sinh { mathfrak {u}} end {align}} left ( Delta ^ {(2)} = { mathfrak {X }} ', Delta ^ {(3)} = { mathfrak {Y}}', Delta ^ {(4)} = { mathfrak {Z}} ' right) { boldsymbol { downarrow}} { begin {align} { mathfrak {X}} '& = X_ {0} -x_ {0} + q_ {x} T { mathfrak {Y}}' & = Y_ {0} -y_ {0} + q_ {y} T b + { mathfrak {Z}} '& = { sqrt { left (Z_ {0} + q_ {x} T right) ^ {2 } -c ^ {2} T ^ {2}} } c { mathfrak {T}} '& = b operatorname {arctanh} { frac {cT} {Z_ {0} + q_ {x} T}} end {align}} left ( X = X_ {0} + q_ {x} T, Y = Y_ {0} + q_ {y} T, Z = Z_ {0} + q_ {x} T right) { boldsymbol { downarrow}} dS ^ {2} = (d { mathfrak {X}} ') ^ {2} + (d { mathfrak {Y}}') ^ {2} + (d { mathfrak {Z }} ') ^ {2} -c ^ {2} left ({ frac {b + { mathfrak {Z}}'} {b ^ {2}}} right) ^ {2} (d { mathfrak {T}} ') ^ {2} end {matrix}}}$
Коттлер (1916, 1918)^{[H 36]}
${ displaystyle scriptstyle { begin {matrix} { begin {align} x & = x ' y & = y' { frac {c ^ {2}} { gamma}} + z & = left ( { frac {c ^ {2}} { gamma}} + z ' right) ch { frac { gamma t'} {c}} ct & = left ({ frac {c ^ { 2}} { gamma}} + z ' right) sinh { frac { gamma t'} {c}} end {align}} { boldsymbol { downarrow}} ds ^ { 2} = dx ^ { prime 2} + dy ^ { prime 2} + dz ^ { prime 2} - left (c + { frac { gamma} {c}} z ' right) {} ^ {2} dt ^ { prime 2} end {matrix}}}$
Паули (1921)^{[H 37]}
${ displaystyle scriptstyle { begin {matrix} { begin {align} x ^ {1} & = varrho cos varphi x ^ {4} & = varrho sin varphi end {выровнено} } { boldsymbol { downarrow}} ds ^ {2} = left (d xi ^ {1} right) ^ {2} + left (d xi ^ {2} right) ^ {2} + left (d xi ^ {3} right) ^ {2} + left ( xi ^ {1} right) ^ {2} left (d xi ^ {4} справа) ^ {2} left ( xi ^ {(1)} = varrho, xi ^ {(2)} = x ^ {(2)}, xi ^ {(3)} = x ^ {(3)}, xi ^ {(4)} = varphi right) end {matrix}}}$
Боллерт (1922)^{[H 20]}
${ displaystyle { scriptstyle { begin {matrix} ds ^ {2} = c ^ {2} left (1 + { frac { gamma _ {0} x} {c ^ {2}}} right ) d tau ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2} hline ds ^ {2} = g_ {44} dx_ {4} ^ {2} + g_ {11} dx_ {1} ^ {2} + g_ {22} left (dx_ {2} ^ {2} + dx_ {3} ^ {2} right) { boldsymbol { downarrow}} V '' - { frac {g_ {11}} {2g_ {11}}} V '= 0 left (g_ {22} = - 1, g_ {11} = - 1, V' '= 0, V = ax + b right) { boldsymbol { downarrow}} ds ^ {2} = dx_ {4} ^ {2} (ax + b) ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2} end {matrix}}}}$
Мохоровичич (1922, 1923); Боллерт (1922b)^{[H 28]}
${ displaystyle { scriptstyle { begin {matrix} { text {Mohorovičić (1922):}} g_ {11} = g_ {44} = V ^ {2}, VV '' - V '^ { 2} = 0, V left (x_ {1} right) = e ^ {ax_ {1}} { boldsymbol { downarrow}} ds ^ {2} = e ^ {2a} left (-dx_ {4} ^ {2} + dx_ {1} ^ {2} right) + dx_ {2} ^ {2} + dx_ {3} ^ {2} { text {исправлено Боллерта (1922b):}} ds ^ {2} = e ^ {2ax} left (-dx_ {4} ^ {2} + dx_ {1} ^ {2} right) + dx_ {2} ^ {2} + dx_ {3} ^ {2} { text {окончательное исправление Мохоровича (1923):}} ds ^ {2} = e ^ {2ax_ {1}} left ( -dx_ {4} ^ {2} + dx_ {1} ^ {2} right) + dx_ {2} ^ {2} + dx_ {3} ^ {2} end {matrix}}}}$
Лемэтр (1924)^{[H 21]}
${ Displaystyle { scriptstyle { begin {matrix} { begin {align} 1 + g xi = & (1 + gx) cosh gt g tau = & (1 + gx) sinh gt end {выровнено}} { boldsymbol { downarrow}} ds ^ {2} = - dx ^ {2} -dy ^ {2} -dz ^ {2} + (1 + gx) ^ {2} dt ^ {2} end {matrix}}}}$
Эйнштейн и Розен (1935)^{[H 22]}
${ Displaystyle scriptstyle { begin {matrix} { begin {align} xi _ {1} & = x_ {1} cosh alpha x_ {4} xi _ {2} & = x_ {2 } xi _ {3} & = x_ {3} xi _ {4} & = x_ {1} sinh alpha x_ {4} end {align}} { boldsymbol { downarrow}} ds ^ {2} = - dx_ {1} ^ {2} -dx_ {2} ^ {2} -dx_ {3} ^ {2} + alpha {} ^ {2} x_ {1 } ^ {2} dx_ {4} ^ {2} end {matrix}}}$
Мёллер (1952)^{[H 23]}
${ displaystyle scriptstyle { begin {matrix} alpha _ {ik} = left ({ begin {matrix} U_ {4} / ic & 0 & 0 & iU_ {1} / c 0 & 1 & 0 & 0 0 & 0 & 1 & 0 U_ {1} / ic & 0 & 0 & U_ {4} / ic end {matrix}} right) U_ {i} = left (c sinh { frac {g tau} {c}}, 0,0, ig cosh { frac {g tau} {c}} right) { boldsymbol { downarrow}} X_ {i} = mathbf {f} _ {i} (t) + x ^ { prime kappa} alpha _ { kappa i} ( tau) { boldsymbol { downarrow}} { begin {align} X & = { frac {c ^ {2}} {g}} left ( ch { frac {gt} {c}} - 1 right) + x cosh { frac {gt} {c}} Y & = y Z & = z T & = { frac {c} {g}} sinh { frac {gt} {c}} + x { frac { sinh { frac {gt} {c}}} {c}} end {align}} { boldsymbol { downarrow}} ds ^ {2} = dx ^ {2} + dy ^ {2} + dz ^ {2} -c ^ {2} dt ^ {2} left (1+ gx / c ^ {2} right) ^ {2} \ end {matrix}}}$
Смотрите также

Парадокс космического корабля Белла За иногда спорный вопрос часто изучаются с помощью координат Риндлера.
Родившиеся координаты, для другой важной системы координат, адаптированной к движению некоторых ускоренных наблюдателей в Пространство-время Минковского.
Конгруэнтность (общая теория относительности)
Парадокс Эренфеста За иногда спорный вопрос часто изучаются с использованием Born координат.
Поля кадра в общей теории относительности
Ресурсы по общей теории относительности
Модель Милна
Уравнение райчаудхури
Эффект Унру
Рекомендации

^ ^а ^б Эйвинд Грен (2010). Конспект лекций по общей теории относительности. Конспект лекций по физике. 772. Springer. С. 86–91. ISBN 978-0387881348.
^ ^а ^б Misner, C.W .; Thorne, K. S .; Уиллер, Дж. А. (1973). Гравитация. Фримен. ISBN 0716703440.
^ Копейкин С., Ефроимский М., Каплан Г. (2011). Релятивистская небесная механика Солнечной системы. Джон Вили и сыновья. ISBN 978-3527408566.CS1 maint: несколько имен: список авторов (связь)
^ Падманабхан, Т. (2010). Гравитация: основы и границы. Издательство Кембриджского университета. ISBN 978-1139485395.
^ Н. Д. Биррелл, П. К. В. Дэвис (1982). Квантовые поля в искривленном пространстве. Кембриджские монографии по математической физике. Издательство Кембриджского университета. ISBN 1107392810.
^ ^а ^б Леонард Сасскинд, Джеймс Линдесей (2005). Введение в черные дыры, информацию и революцию теории струн: голографическая Вселенная. World Scientific. С. 8–10. ISBN 9812561315.
^ Муньос, Херардо; Джонс, Престон (2010). «Принцип эквивалентности, равноускоренные системы отсчета и однородное гравитационное поле». Американский журнал физики. 78 (4): 377–383. arXiv:1003.3022. Bibcode:2010AmJPh..78..377M. Дои:10.1119/1.3272719. S2CID 118616525.
^ ^а ^б ^c Мингуцци, Э. (2005). «Метрика Минковского в координатах неинерциального радара наблюдателя». Американский журнал физики. 73 (12): 1117–1121. arXiv:физика / 0412024. Bibcode:2005AmJPh..73.1117M. Дои:10.1119/1.2060716. S2CID 119359878.
^ ^а ^б ^c ^d Дэвид Тилбрук (1997). "Общие координаты плоского пространства-времени постоянного собственного ускорения". Австралийский журнал физики. 50 (5): 851–868. Дои:10.1071 / P96111.
^ Джонс, Престон; Ванекс, Лукас Ф. (2006). «Парадокс часов в статическом однородном гравитационном поле». Основы письма по физике. 19 (1): 75–85. arXiv:физика / 0604025. Bibcode:2006ФоФЛ..19 ... 75J. Дои:10.1007 / s10702-006-1850-3. S2CID 14583590.
^ Например, Birrell & Davies (1982), стр. 110-111 или Padmanabhan (2010), стр. 126 обозначают уравнения (2 г, 2ч) как координаты Риндлера или кадр Риндлера; Tilbrook (1997) pp. 864-864 или Jones & Wanex (2006) обозначают уравнения (2а, 2b) как координаты Риндлера
^ ^а ^б Рорлих, Фриц (1963). «Принцип эквивалентности». Анналы физики. 22 (2): 169–191. Bibcode:1963AnPhy..22..169R. Дои:10.1016/0003-4916(63)90051-4.
^ ^а ^б Гарри Ласс (1963). «Ускорение системы отсчета и парадокс часов». Американский журнал физики. 31 (4): 274–276. Bibcode:1963AmJPh..31..274L. Дои:10.1119/1.1969430.
^ ^а ^б Риндлер, В. (1960). «Гиперболическое движение в искривленном пространстве-времени». Физический обзор. 119 (6): 2082–2089. Bibcode:1960ПхРв..119.2082Р. Дои:10.1103 / PhysRev.119.2082.
^ ^а ^б ^c Риндлер, В. (1966). «Пространство Крускала и равномерно ускоренный фрейм». Американский журнал физики. 34 (12): 1174–1178. Bibcode:1966AmJPh..34.1174R. Дои:10.1119/1.1972547.
^ ^а ^б Паули, Вольфганг (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften, 5 (2): 539–776
По-английски: Паули, В. (1981) [1921]. Теория относительности. Фундаментальные теории физики. 165. Dover Publications. ISBN 0-486-64152-X.
^ фон Лауэ, М. (1921). Die Relativitätstheorie, группа 1 (четвертое издание "Das Relativitätsprinzip" изд.). Vieweg.; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.
^ ^а ^б Дон Кокс (2006). Исследования по математической физике. Springer. С. 235–269. ISBN 0387309438.
^ Мёллер, К. (1955) [1952]. Теория относительности. Oxford Clarendon Press.
^ Мёллер (1952), ур. 154
^ Misner & Thorne & Wheeler (1973), раздел 6.6
^ Муньос и Джонс (2010), ур. 37, 38
^ Паули (1921), раздел 32-й
^ Риндлер (1966), стр. 1177
^ Массимо Паури, Микеле Валлиснери (2000). «Координаты Мерцке-Уиллера для ускоренных наблюдателей в специальной теории относительности». Основы письма по физике. 13 (5): 401–425. arXiv:gr-qc / 0006095. Bibcode:2000гр.кв ..... 6095П. Дои:10.1023 / А: 1007861914639. S2CID 15097773.
^ Долби, Карл Э .; Чайка, Стивен Ф. (2001). Парадокс "на радаре время и близнец""". Американский журнал физики. 69 (12): 1257–1261. arXiv:gr-qc / 0104077. Bibcode:2001AmJPh..69.1257D. Дои:10.1119/1.1407254. S2CID 119067219.
^ Блюм, А.С., Ренн, Дж., Солсбери, Д. К., Шеммель, М., и Сандермейер, К. (2012). «1912 год: поворотный момент на пути Эйнштейна к общей теории относительности». Annalen der Physik. 524 (1): A12 – A13. Bibcode:2012AnP ... 524A..11B. Дои:10.1002 / andp.201100705.CS1 maint: несколько имен: список авторов (связь)
^ Desloge, Эдвард А .; Филпотт, Р. Дж. (1987). «Равномерно ускоренные системы отсчета в специальной теории относительности». Американский журнал физики. 55 (3): 252–261. Bibcode:1987AmJPh..55..252D. Дои:10.1119/1.15197.
^ Herglotz (1909), стр. 408, 414
Исторические источники

^ ^а ^б Родился Макс (1909). "Теория звездных электронов в кинематике релятивистских принтов" [Перевод Wikisource: Теория жесткого электрона в кинематике принципа относительности ]. Annalen der Physik. 335 (11): 1–56. Bibcode:1909АнП ... 335 .... 1Б. Дои:10.1002 / andp.19093351102.
^ ^а ^б Эйнштейн, Альберт (1908) [1907], "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen" (PDF), Jahrbuch der Radioaktivität und Elektronik, 4: 411–462, Bibcode:1908JRE ..... 4..411E; английский перевод О принципе относительности и сделанных из него выводах в бумажном проекте Эйнштейна.Эйнштейн, Альберт (1912), "Lichtgeschwindigkeit und Statik des Gravitationsfeldes", Annalen der Physik, 343 (7): 355–369, Bibcode:1912АнП ... 343..355E, Дои:10.1002 / andp.19123430704, Английский перевод Скорость света и статика гравитационного поля в бумажном проекте Эйнштейна.
^ ^а ^б Зоммерфельд, Арнольд (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [Перевод Wikisource: К теории относительности II: четырехмерный векторный анализ ]. Annalen der Physik. 338 (14): 649–689. Bibcode:1910АнП ... 338..649С. Дои:10.1002 / andp.19103381402.
^ Лауэ, Макс фон (1911). Das Relativitätsprinzip. Брауншвейг: Vieweg.
^ Лоренц, Хендрик Антон (1914) [1913]. Das Relativitätsprinzip. Drei Vorlesungen gehalten в Teylers Stiftung zu Haarlem (1913) . Лейпциг / Берлин: B.G. Teubner.
^ Коттлер, Фридрих (1912). "Über die Raumzeitlinien der Minkowski'schen Welt" [перевод Wikisource: На пространственно-временных линиях мира Минковского ]. Wiener Sitzungsberichte 2a. 121: 1659–1759. HDL:2027 / mdp.39015051107277.Коттлер, Фридрих (1914a). "Relativitätsprinzip und beschleunigte Bewegung". Annalen der Physik. 349 (13): 701–748. Bibcode:1914АнП ... 349..701К. Дои:10.1002 / andp.19143491303.Коттлер, Фридрих (1914b). "Fallende Bezugssysteme vom Standpunkte des Relativitätsprinzips". Annalen der Physik. 350 (20): 481–516. Bibcode:1914АнП ... 350..481К. Дои:10.1002 / andp.19143502003.Коттлер, Фридрих (1916). "Über Einsteins Äquivalenzhypothese und die Gravitation". Annalen der Physik. 355 (16): 955–972. Bibcode:1916АнП ... 355..955К. Дои:10.1002 / andp.19163551605.Коттлер, Фридрих (1918). "Uber die Physikalischen Grundlagen der Einsteinschen Relativitätstheorie". Annalen der Physik. 361 (14): 401–461. Bibcode:1918АнП ... 361..401К. Дои:10.1002 / иp.19183611402.
^ Паули, В. (1921). "Die Relativitätstheorie". Encyclopädie der Mathematischen Wissenschaften. 5. С. 539–776. Новое издание 2013 г .: Редактор: Доменико Джулини, Springer, 2013 г. ISBN 3642583555.
^ Карл Боллерт (1922а). "Однородные гравитационные поля и преобразования Lorentztransformationen". Zeitschrift für Physik. 10 (1): 256–266. Bibcode:1922ZPhy ... 10..256B. Дои:10.1007 / BF01332567. S2CID 122965400.Карл Боллерт (1922b). "Die Entstehung der Lorentzverkürzung und die strenge Behandlung des Uhrenparadoxons". Zeitschrift für Physik. 12 (1): 189–206. Bibcode:1923ZPhy ... 12..189B. Дои:10.1007 / BF01328090. S2CID 120603392.
^ Мохорович, С. (1922). "Das" гомогенный "Gravitationsfeld und die Lorentztransformation". Zeitschrift für Physik. 11 (1): 88–92. Bibcode:1922ZPhy ... 11 ... 88M. Дои:10.1007 / BF01328404. S2CID 123661029.Мохорович, С. (1923). "Äther, Materie, Gravitation und Relativitätstheorie". Zeitschrift für Physik. 18 (1): 34–63. Bibcode:1923ZPhy ... 18 ... 34M. Дои:10.1007 / BF01327684. S2CID 123728700.
^ Лемэтр, Г. (1924), "Движение твердого тела в соответствии с принципом относительности", Философский журнал, Серия 6, 48 (283): 164–176, Дои:10.1080/14786442408634478
^ ^а ^б Мёллер, К. (1943). «Об однородных гравитационных полях в общей теории относительности и парадоксе часов». Дэн. Мат. Fys. Medd. 8: 3–25.Мёллер, К. (1955) [1952]. Теория относительности. Oxford Clarendon Press.
^ Коттлер (1914b), стр. 488-489, 492-493
^ Эйнштейн, Альберт; Розен, Натан (1935). «Проблема частиц в общей теории относительности». Физический обзор. 48 (1): 73–77. Bibcode:1935ПхРв ... 48 ... 73Э. Дои:10.1103 / PhysRev.48.73.
^ ^а ^б Родился (1909), стр. 25
^ ^а ^б Зоммерфельд (1910), стр. 670-671
^ фон Лауэ, М. (1921). Die Relativitätstheorie, группа 1 (четвертое издание "Das Relativitätsprinzip" изд.). Vieweg.; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.
^ ^а ^б Эйнштейн (1912), стр. 358-359.
^ ^а ^б Lorentz (1913), стр. 34–38; 50-52
^ Kottler (1912), стр. 1715; Коттлер (1914a), Таблица I; стр. 747–748; Коттлер (1914b), стр. 488–489, 503; Коттлер (1916), стр. 958–959; (1918), стр. 453–454;
^ ^а ^б Боллерт (1922a), стр. 261, 266
^ ^а ^б Леметр (1921), стр. 166, 168
^ ^а ^б Эйнштейн и Розен (1935, с. 74).
^ ^а ^б Møller (1952), стр. 121–123; 255–258
^ Родился (1909), стр. 35 год
^ Зоммерфельд (1910), стр. 672
^ Коттлер (1914), стр. 489-490.
^ Боллерт (1922b), стр. 194-196.
^ ^а ^б Мохоровичич (1922), стр. 92, без ${ displaystyle x_ {1}}$ в показателе экспоненты из-за опечатки, которую исправили Боллерт (1922b), стр. 189, а также Мохорович (1923), стр. 54
^ Боллерт (1922b), стр. 189
^ Эйнштейн (1907), §§ 18-21.
^ Херглотц, Густав (1910) [1909], "Über den vom Standpunkt des Relativitätsprinzips aus als starr zu bezeichnenden Körper" [Перевод Wikisource: О телах, которые следует обозначить как «твердые» с точки зрения принципа относительности ], Annalen der Physik, 336 (2): 393–415, Bibcode:1910AnP ... 336..393H, Дои:10.1002 / andp.19103360208
^ фон Лауэ (1911), стр. 109
^ Коттлер (1912), стр 1715
^ Коттлер (1914a), Таблица I; стр. 747-748
^ Коттлер (1914b), стр. 488-489, 503
^ Kottler (1916), стр. 958-959; (1918), стр. 453-454.
^ Паули (1921), стр. 647-648.
дальнейшее чтение

Полезный фон:
Бутби, Уильям М. (1986). Введение в дифференцируемые многообразия и риманову геометрию. Нью-Йорк: Academic Press. ISBN 0-12-116052-1. Видеть Глава 4 для справки о векторных полях на гладких многообразиях.
Франкель, Теодор (1979). Гравитационная кривизна: введение в теорию Эйнштейна. Сан-Франциско: В. Х. Фриман. ISBN 0-7167-1062-5. Видеть Глава 8 для вывода метрики Ферма.
Координаты Риндлера:
Риндлер, Вольфганг (1969). Основная теория относительности. Нью-Йорк, Van Nostrand Reinhold Co. Дои:10.1007/978-1-4757-1135-6. ISBN 978-0-387-90201-2.
Миснер, Чарльз; Торн, Кип С. и Уиллер, Джон Арчибальд (1973). Гравитация. Сан-Франциско: В. Х. Фриман. ISBN 0-7167-0344-0. Видеть Раздел 6.6.
Риндлер, Вольфганг (2001). Теория относительности: специальная, общая и космологическая. Оксфорд: Издательство Оксфордского университета. ISBN 0-19-850836-0.
Ни, Вэй-Тоу; Циммерманн, Марк (1978). «Инерционные и гравитационные эффекты в надлежащей системе отсчета ускоренного вращающегося наблюдателя». Физический обзор D. 17 (6): 1473–1476. Bibcode:1978ПхРвД..17.1473Н. Дои:10.1103 / PhysRevD.17.1473.
Горизонт Риндлера:
Якобсон, Тед и Паренти, Рено (2003). «Горизонт Энтропия». Найденный. Phys. 33 (2): 323–348. Дои:10.1023 / А: 1023785123428. S2CID 16826867. версия для печати
Барсело, Карлос; Либерати, Стефано и Виссер, Мэтт (2005). «Аналог гравитации». Живые обзоры в теории относительности. 8 (1): 12. arXiv:gr-qc / 0505065. Bibcode:2005ЛРР ..... 8 ... 12Б. Дои:10.12942 / lrr-2005-12. ЧВК 5255570. PMID 28179871.

[Gron-2] а ^б Эйвинд Грен (2010). Конспект лекций по общей теории относительности. Конспект лекций по физике. 772. Springer. С. 86–91. ISBN 978-0387881348.

[mtw-3] а ^б Misner, C.W .; Thorne, K. S .; Уиллер, Дж. А. (1973). Гравитация. Фримен. ISBN 0716703440.

[Kop-4] Копейкин С., Ефроимский М., Каплан Г. (2011). Релятивистская небесная механика Солнечной системы. Джон Вили и сыновья. ISBN 978-3527408566.CS1 maint: несколько имен: список авторов (связь)

[Padma-5] Падманабхан, Т. (2010). Гравитация: основы и границы. Издательство Кембриджского университета. ISBN 978-1139485395.

[Birrell-6] Н. Д. Биррелл, П. К. В. Дэвис (1982). Квантовые поля в искривленном пространстве. Кембриджские монографии по математической физике. Издательство Кембриджского университета. ISBN 1107392810.

[Susskind-7] а ^б Леонард Сасскинд, Джеймс Линдесей (2005). Введение в черные дыры, информацию и революцию теории струн: голографическая Вселенная. World Scientific. С. 8–10. ISBN 9812561315.

[Munoz-8] Муньос, Херардо; Джонс, Престон (2010). «Принцип эквивалентности, равноускоренные системы отсчета и однородное гравитационное поле». Американский журнал физики. 78 (4): 377–383. arXiv:1003.3022. Bibcode:2010AmJPh..78..377M. Дои:10.1119/1.3272719. S2CID 118616525.

[Minguzzi-9] а ^б ^c Мингуцци, Э. (2005). «Метрика Минковского в координатах неинерциального радара наблюдателя». Американский журнал физики. 73 (12): 1117–1121. arXiv:физика / 0412024. Bibcode:2005AmJPh..73.1117M. Дои:10.1119/1.2060716. S2CID 119359878.

[Tilbrook-10] а ^б ^c ^d Дэвид Тилбрук (1997). "Общие координаты плоского пространства-времени постоянного собственного ускорения". Австралийский журнал физики. 50 (5): 851–868. Дои:10.1071 / P96111.

[Jones-11] Джонс, Престон; Ванекс, Лукас Ф. (2006). «Парадокс часов в статическом однородном гравитационном поле». Основы письма по физике. 19 (1): 75–85. arXiv:физика / 0604025. Bibcode:2006ФоФЛ..19 ... 75J. Дои:10.1007 / s10702-006-1850-3. S2CID 14583590.

[12] Например, Birrell & Davies (1982), стр. 110-111 или Padmanabhan (2010), стр. 126 обозначают уравнения (2 г, 2ч) как координаты Риндлера или кадр Риндлера; Tilbrook (1997) pp. 864-864 или Jones & Wanex (2006) обозначают уравнения (2а, 2b) как координаты Риндлера

[Rohrlich-23] а ^б Рорлих, Фриц (1963). «Принцип эквивалентности». Анналы физики. 22 (2): 169–191. Bibcode:1963AnPhy..22..169R. Дои:10.1016/0003-4916(63)90051-4.

[Lass-24] а ^б Гарри Ласс (1963). «Ускорение системы отсчета и парадокс часов». Американский журнал физики. 31 (4): 274–276. Bibcode:1963AmJPh..31..274L. Дои:10.1119/1.1969430.

[Rindler1-25] а ^б Риндлер, В. (1960). «Гиперболическое движение в искривленном пространстве-времени». Физический обзор. 119 (6): 2082–2089. Bibcode:1960ПхРв..119.2082Р. Дои:10.1103 / PhysRev.119.2082.

[Rindler2-26] а ^б ^c Риндлер, В. (1966). «Пространство Крускала и равномерно ускоренный фрейм». Американский журнал физики. 34 (12): 1174–1178. Bibcode:1966AmJPh..34.1174R. Дои:10.1119/1.1972547.

[Pauli-27] а ^б Паули, Вольфганг (1921), "Die Relativitätstheorie", Encyclopädie der Mathematischen Wissenschaften, 5 (2): 539–776
По-английски: Паули, В. (1981) [1921]. Теория относительности. Фундаментальные теории физики. 165. Dover Publications. ISBN 0-486-64152-X.

[Laue2-28] фон Лауэ, М. (1921). Die Relativitätstheorie, группа 1 (четвертое издание "Das Relativitätsprinzip" изд.). Vieweg.; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.

[Koks-29] а ^б Дон Кокс (2006). Исследования по математической физике. Springer. С. 235–269. ISBN 0387309438.

[Møller-30] Мёллер, К. (1955) [1952]. Теория относительности. Oxford Clarendon Press.

[32] Мёллер (1952), ур. 154

[33] Misner & Thorne & Wheeler (1973), раздел 6.6

[34] Муньос и Джонс (2010), ур. 37, 38

[35] Паули (1921), раздел 32-й

[36] Риндлер (1966), стр. 1177

[Pauri-37] Массимо Паури, Микеле Валлиснери (2000). «Координаты Мерцке-Уиллера для ускоренных наблюдателей в специальной теории относительности». Основы письма по физике. 13 (5): 401–425. arXiv:gr-qc / 0006095. Bibcode:2000гр.кв ..... 6095П. Дои:10.1023 / А: 1007861914639. S2CID 15097773.

[Dolby-38] Долби, Карл Э .; Чайка, Стивен Ф. (2001). Парадокс "на радаре время и близнец""". Американский журнал физики. 69 (12): 1257–1261. arXiv:gr-qc / 0104077. Bibcode:2001AmJPh..69.1257D. Дои:10.1119/1.1407254. S2CID 119067219.

[Blum-44] Блюм, А.С., Ренн, Дж., Солсбери, Д. К., Шеммель, М., и Сандермейер, К. (2012). «1912 год: поворотный момент на пути Эйнштейна к общей теории относительности». Annalen der Physik. 524 (1): A12 – A13. Bibcode:2012AnP ... 524A..11B. Дои:10.1002 / andp.201100705.CS1 maint: несколько имен: список авторов (связь)

[Desloge-57] Desloge, Эдвард А .; Филпотт, Р. Дж. (1987). «Равномерно ускоренные системы отсчета в специальной теории относительности». Американский журнал физики. 55 (3): 252–261. Bibcode:1987AmJPh..55..252D. Дои:10.1119/1.15197.

[60] Herglotz (1909), стр. 408, 414

[born-1] а ^б Родился Макс (1909). "Теория звездных электронов в кинематике релятивистских принтов" [Перевод Wikisource: Теория жесткого электрона в кинематике принципа относительности ]. Annalen der Physik. 335 (11): 1–56. Bibcode:1909АнП ... 335 .... 1Б. Дои:10.1002 / andp.19093351102.

[Einstein-13] а ^б Эйнштейн, Альберт (1908) [1907], "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen" (PDF), Jahrbuch der Radioaktivität und Elektronik, 4: 411–462, Bibcode:1908JRE ..... 4..411E; английский перевод О принципе относительности и сделанных из него выводах в бумажном проекте Эйнштейна.Эйнштейн, Альберт (1912), "Lichtgeschwindigkeit und Statik des Gravitationsfeldes", Annalen der Physik, 343 (7): 355–369, Bibcode:1912АнП ... 343..355E, Дои:10.1002 / andp.19123430704, Английский перевод Скорость света и статика гравитационного поля в бумажном проекте Эйнштейна.

[Sommerfeld-14] а ^б Зоммерфельд, Арнольд (1910). "Zur Relativitätstheorie II: Vierdimensionale Vektoranalysis" [Перевод Wikisource: К теории относительности II: четырехмерный векторный анализ ]. Annalen der Physik. 338 (14): 649–689. Bibcode:1910АнП ... 338..649С. Дои:10.1002 / andp.19103381402.

[Laue-15] Лауэ, Макс фон (1911). Das Relativitätsprinzip. Брауншвейг: Vieweg.

[Lorentz-16] Лоренц, Хендрик Антон (1914) [1913]. Das Relativitätsprinzip. Drei Vorlesungen gehalten в Teylers Stiftung zu Haarlem (1913) . Лейпциг / Берлин: B.G. Teubner.

[Kottler-17] Коттлер, Фридрих (1912). "Über die Raumzeitlinien der Minkowski'schen Welt" [перевод Wikisource: На пространственно-временных линиях мира Минковского ]. Wiener Sitzungsberichte 2a. 121: 1659–1759. HDL:2027 / mdp.39015051107277.Коттлер, Фридрих (1914a). "Relativitätsprinzip und beschleunigte Bewegung". Annalen der Physik. 349 (13): 701–748. Bibcode:1914АнП ... 349..701К. Дои:10.1002 / andp.19143491303.Коттлер, Фридрих (1914b). "Fallende Bezugssysteme vom Standpunkte des Relativitätsprinzips". Annalen der Physik. 350 (20): 481–516. Bibcode:1914АнП ... 350..481К. Дои:10.1002 / andp.19143502003.Коттлер, Фридрих (1916). "Über Einsteins Äquivalenzhypothese und die Gravitation". Annalen der Physik. 355 (16): 955–972. Bibcode:1916АнП ... 355..955К. Дои:10.1002 / andp.19163551605.Коттлер, Фридрих (1918). "Uber die Physikalischen Grundlagen der Einsteinschen Relativitätstheorie". Annalen der Physik. 361 (14): 401–461. Bibcode:1918АнП ... 361..401К. Дои:10.1002 / иp.19183611402.

[Pauli-18] Паули, В. (1921). "Die Relativitätstheorie". Encyclopädie der Mathematischen Wissenschaften. 5. С. 539–776. Новое издание 2013 г .: Редактор: Доменико Джулини, Springer, 2013 г. ISBN 3642583555.

[Bollert-19] Карл Боллерт (1922а). "Однородные гравитационные поля и преобразования Lorentztransformationen". Zeitschrift für Physik. 10 (1): 256–266. Bibcode:1922ZPhy ... 10..256B. Дои:10.1007 / BF01332567. S2CID 122965400.Карл Боллерт (1922b). "Die Entstehung der Lorentzverkürzung und die strenge Behandlung des Uhrenparadoxons". Zeitschrift für Physik. 12 (1): 189–206. Bibcode:1923ZPhy ... 12..189B. Дои:10.1007 / BF01328090. S2CID 120603392.

[Mohoro-20] Мохорович, С. (1922). "Das" гомогенный "Gravitationsfeld und die Lorentztransformation". Zeitschrift für Physik. 11 (1): 88–92. Bibcode:1922ZPhy ... 11 ... 88M. Дои:10.1007 / BF01328404. S2CID 123661029.Мохорович, С. (1923). "Äther, Materie, Gravitation und Relativitätstheorie". Zeitschrift für Physik. 18 (1): 34–63. Bibcode:1923ZPhy ... 18 ... 34M. Дои:10.1007 / BF01327684. S2CID 123728700.

[Lemaitre-21] Лемэтр, Г. (1924), "Движение твердого тела в соответствии с принципом относительности", Философский журнал, Серия 6, 48 (283): 164–176, Дои:10.1080/14786442408634478

[Møller-22] а ^б Мёллер, К. (1943). «Об однородных гравитационных полях в общей теории относительности и парадоксе часов». Дэн. Мат. Fys. Medd. 8: 3–25.Мёллер, К. (1955) [1952]. Теория относительности. Oxford Clarendon Press.

[31] Коттлер (1914b), стр. 488-489, 492-493

[Einstein2-39] Эйнштейн, Альберт; Розен, Натан (1935). «Проблема частиц в общей теории относительности». Физический обзор. 48 (1): 73–77. Bibcode:1935ПхРв ... 48 ... 73Э. Дои:10.1103 / PhysRev.48.73.

[born2-40] а ^б Родился (1909), стр. 25

[Sommerfeld2-41] а ^б Зоммерфельд (1910), стр. 670-671

[Laue2-42] фон Лауэ, М. (1921). Die Relativitätstheorie, группа 1 (четвертое издание "Das Relativitätsprinzip" изд.). Vieweg.; Первое издание 1911 г., второе расширенное издание 1913 г., третье расширенное издание 1919 г.

[Einstein5-43] а ^б Эйнштейн (1912), стр. 358-359.

[Lorentz2-45] а ^б Lorentz (1913), стр. 34–38; 50-52

[Kottler2-46] Kottler (1912), стр. 1715; Коттлер (1914a), Таблица I; стр. 747–748; Коттлер (1914b), стр. 488–489, 503; Коттлер (1916), стр. 958–959; (1918), стр. 453–454;

[Bollert2-47] а ^б Боллерт (1922a), стр. 261, 266

[Lemaitre2-48] а ^б Леметр (1921), стр. 166, 168

[Einstein4-49] а ^б Эйнштейн и Розен (1935, с. 74).

[Møller2-50] а ^б Møller (1952), стр. 121–123; 255–258

[51] Родился (1909), стр. 35 год

[52] Зоммерфельд (1910), стр. 672

[53] Коттлер (1914), стр. 489-490.

[54] Боллерт (1922b), стр. 194-196.

[Mohoro2-55] а ^б Мохоровичич (1922), стр. 92, без ${ displaystyle x_ {1}}$ в показателе экспоненты из-за опечатки, которую исправили Боллерт (1922b), стр. 189, а также Мохорович (1923), стр. 54

[56] Боллерт (1922b), стр. 189

[Einstein3-58] Эйнштейн (1907), §§ 18-21.

[Herglotz-59] Херглотц, Густав (1910) [1909], "Über den vom Standpunkt des Relativitätsprinzips aus als starr zu bezeichnenden Körper" [Перевод Wikisource: О телах, которые следует обозначить как «твердые» с точки зрения принципа относительности ], Annalen der Physik, 336 (2): 393–415, Bibcode:1910AnP ... 336..393H, Дои:10.1002 / andp.19103360208

[61] фон Лауэ (1911), стр. 109

[62] Коттлер (1912), стр 1715

[63] Коттлер (1914a), Таблица I; стр. 747-748

[64] Коттлер (1914b), стр. 488-489, 503

[65] Kottler (1916), стр. 958-959; (1918), стр. 453-454.

[Pauli2-66] Паули (1921), стр. 647-648.

[H 1]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[H 2]

[H 3]

[H 4]

[H 5]

[H 6]

[H 7]

[H 8]

[H 9]

[H 10]

[H 11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[H 12]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[H 13]

[H 14]

[H 15]

[H 16]

[H 17]

[27]

[H 18]

[H 19]

[H 20]

[H 21]

[H 22]

[H 23]

[H 24]

[H 25]

[H 26]

[H 27]

[H 28]

[H 29]

[28]

[H 30]

[H 31]

[29]

[H 32]

[H 33]

[H 34]

[H 35]

[H 36]

[H 37]