Самоорганизующаяся карта - Википедия - Self-organizing map

Часть серии по
Машинное обучение
и
сбор данных

А самоорганизующаяся карта (SOM) или же самоорганизующаяся карта объектов (SOFM) является разновидностью искусственная нейронная сеть (ИНС), который обучается с использованием обучение без учителя для создания низкоразмерного (обычно двумерного) дискретного представления входного пространства обучающих выборок, называемого карта, и, следовательно, это способ сделать уменьшение размерности. Самоорганизующиеся карты отличаются от других искусственных нейронных сетей своим применением соревновательное обучение в отличие от обучения с исправлением ошибок (например, обратное распространение с градиентный спуск ), и в том смысле, что они используют функцию соседства для сохранения топологический свойства входного пространства.

Самоорганизующаяся карта, показывающая Конгресс США схемы голосования. Входными данными была таблица со строкой для каждого члена Конгресса и столбцами для определенных голосов, содержащими голоса каждого члена «да» / «нет» / «воздержался». Алгоритм SOM ​​расположил эти элементы в двумерной сетке, расположив аналогичные элементы ближе друг к другу. Первый сюжет показывает группировку, когда данные разделены на два кластера. Второй сюжет показывает среднее расстояние до соседей: большие расстояния темнее. Третий сюжет предсказывает Республиканец (красный) или Демократичный (синий) членство в партии. Остальные сюжеты каждый накладывает полученную карту с прогнозируемыми значениями во входном измерении: красный цвет означает прогнозируемое голосование «да» по этому законопроекту, синий означает голосование «нет». Сюжет создан в Синапс.

Это делает SOM полезными для визуализация путем создания низкоразмерных представлений многомерных данных, похожих на многомерное масштабирование. Искусственная нейронная сеть, представленная Финский профессор Теуво Кохонен в 80-е годы иногда называют Карта Кохонена или же сеть.[1][2] Сеть Кохонена - это удобная в вычислительном отношении абстракция, построенная на биологических моделях нейронных систем 1970-х годов.[3] и морфогенез модели, относящиеся к Алан Тьюринг в 1950-е гг.[4]

Хотя типично рассматривать этот тип сетевой структуры как относящуюся к сети прямого распространения там, где узлы визуализируются прикрепленными, этот тип архитектуры принципиально отличается по расположению и мотивации.

Полезные расширения включают использование тороидальный сетки, в которых соединены противоположные ребра и использующие большое количество узлов.

Также часто используется U-матрица.[5] Значение U-матрицы конкретного узла - это среднее расстояние между вектором веса узла и его ближайшими соседями.[6] В квадратной сетке, например, можно рассматривать ближайшие 4 или 8 узлов ( Фон Нейман и Окрестности Мура соответственно) или шесть узлов в гексагональной сетке.

Большой дисплей SOM эмерджентные свойства. В картах, состоящих из тысяч узлов, можно выполнять кластерные операции на самой карте.[7]

Структура и операции

Как и большинство искусственных нейронных сетей, SOM работают в двух режимах: обучение и отображение. «Обучение» строит карту, используя примеры ввода ( конкурентный процесс, также называемый векторное квантование ), в то время как «отображение» автоматически классифицирует новый входной вектор.

Видимая часть самоорганизующейся карты - это пространство карты, которое состоит из компонентов, называемых узлами или нейронами. Пространство карты определяется заранее, обычно как конечная двумерная область, где узлы расположены в регулярном порядке. шестиугольник или же прямоугольный сетка.[8] Каждый узел связан с вектором «веса», который является позицией во входном пространстве; то есть он имеет ту же размерность, что и каждый входной вектор. Пока узлы в пространстве карты остаются фиксированными, обучение заключается в перемещении векторов весов к входным данным (уменьшение метрики расстояния) без нарушения топологии, созданной из пространства карты. Таким образом, самоорганизующаяся карта описывает отображение из входного пространства более высокого измерения в пространство карты более низкого измерения. После обучения карта может классифицировать вектор из входного пространства, найдя узел с ближайшим (с наименьшей метрикой расстояния) весовым вектором к вектору входного пространства.

Алгоритм обучения

Цель обучения самоорганизующейся карте - заставить разные части сети одинаково реагировать на определенные входные шаблоны. Частично это мотивировано тем, как зрительные, слуховые или другие сенсорный информация обрабатывается в отдельных частях кора головного мозга в человеческий мозг.[9]

Иллюстрация тренировки самоорганизующейся карты. Голубая капля - это распределение обучающих данных, а маленький белый диск - текущие обучающие данные, взятые из этого распределения. Сначала (слева) узлы SOM произвольно располагаются в пространстве данных. Выбирается ближайший к обучающей базе узел (выделен желтым). Он перемещается к обучающей базе данных, поскольку (в меньшей степени) является ее соседями по сетке. После многих итераций сетка приближается к распределению данных (справа).

Веса нейронов инициализируются либо небольшими случайными значениями, либо выбираются равномерно из подпространства, охватываемого двумя самыми большими главный компонент собственные векторы. С последним вариантом обучение происходит намного быстрее, потому что начальные веса уже дают хорошее приближение к весам SOM.[10]

В сеть необходимо подавать большое количество примеров векторов, которые максимально точно представляют типы векторов, ожидаемых во время отображения. Примеры обычно вводятся несколько раз в виде итераций.

Тренинг использует соревновательное обучение. Когда обучающий пример передается в сеть, его Евклидово расстояние ко всем весовым векторам. Нейрон, весовой вектор которого наиболее похож на входной, называется лучший соответствующий блок (БМУ). Веса BMU и близких к нему нейронов в сетке SOM корректируются по входному вектору. Величина изменения уменьшается со временем и с удалением сетки от BMU. Формула обновления для нейрона v с вектором весов Wv(s) это

,

где s - индекс шага, t - индекс обучающей выборки, u - индекс BMU для входного вектора. D(t), α (s) - это монотонно убывающий коэффициент обучения; Θ (u, v, s) - функция соседства, которая дает расстояние между нейроном u и нейроном v на шаге s.[11] В зависимости от реализаций t может систематически сканировать набор обучающих данных (t - 0, 1, 2 ... T-1, затем повторять, T - размер обучающей выборки), случайным образом извлекаться из набора данных (выборка начальной загрузки ) или реализовать какой-либо другой метод выборки (например, складной нож ).

Функция соседства Θ (u, v, s) (также называемая функция бокового взаимодействия) зависит от расстояния по сетке между BMU (нейрон ты) и нейрон v. В простейшей форме это 1 для всех нейронов, достаточно близких к BMU и 0 для других, но Гауссовский и мексиканская шляпа[12] функции также являются обычным выбором. Независимо от функциональной формы, функция соседства сжимается со временем.[9] Вначале, когда окружение велико, самоорганизация происходит в глобальном масштабе. Когда соседство сократилось до пары нейронов, веса сходятся к локальным оценкам. В некоторых реализациях коэффициент обучения α и функция соседства Θ неуклонно уменьшаются с увеличением s, в других (в частности, в тех, где t сканирует набор обучающих данных) они уменьшаются пошагово, один раз каждые T шагов.

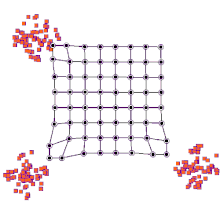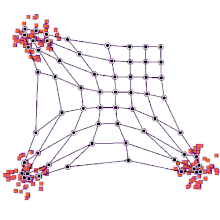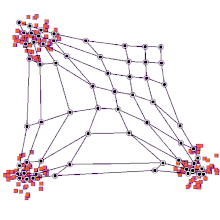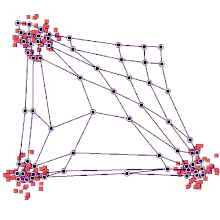
Процесс обучения СОМ на двумерном наборе данных

Этот процесс повторяется для каждого входного вектора в течение (обычно большого) количества циклов. λ. В итоге сеть связывает выходные узлы с группами или шаблонами во входном наборе данных. Если эти шаблоны могут быть названы, имена могут быть присоединены к связанным узлам в обученной сети.

Во время отображения будет один сингл победа нейрон: нейрон, весовой вектор которого находится ближе всего к входному вектору. Это можно просто определить, вычислив евклидово расстояние между входным вектором и вектором весов.

Хотя в этой статье было подчеркнуто представление входных данных в виде векторов, любой тип объекта, который может быть представлен в цифровом виде, с которым связана соответствующая мера расстояния и в котором возможны необходимые операции для обучения, может быть использован для построения собственного -организация карты. Сюда входят матрицы, непрерывные функции или даже другие самоорганизующиеся карты.

Переменные

Это необходимые переменные, векторы выделены жирным шрифтом,

  • это текущая итерация
  • это предел итераций
  • - это индекс вектора целевых входных данных во входном наборе данных
  • целевой вектор входных данных
  • это индекс узла на карте
  • текущий весовой вектор узла
  • это индекс единицы наилучшего соответствия (BMU) на карте
  • является ограничением из-за расстояния от BMU, обычно называемого функцией соседства, и
  • - это ограничение обучения из-за прогресса итерации.

Алгоритм

  1. Рандомизируйте весовые векторы узлов на карте
  2. Случайно выберите входной вектор
  3. Пройдите по каждому узлу на карте
    1. Использовать Евклидово расстояние формула, чтобы найти сходство между входным вектором и вектором веса узла карты
    2. Отслеживайте узел, который производит наименьшее расстояние (этот узел является наиболее подходящей единицей, BMU)
  4. Обновите весовые векторы узлов в окрестности BMU (включая сам BMU), подтянув их ближе к входному вектору
  5. Увеличивать и повторите, начиная с шага 2, пока

Вариант алгоритма:

  1. Рандомизируйте весовые векторы узлов карты
  2. Просмотрите каждый входной вектор во входном наборе данных
    1. Пройдите по каждому узлу на карте
      1. Использовать Евклидово расстояние формула, чтобы найти сходство между входным вектором и вектором веса узла карты
      2. Отслеживайте узел, который производит наименьшее расстояние (этот узел является наиболее подходящей единицей, BMU)
    2. Обновите узлы в окрестности BMU (включая сам BMU), подтянув их ближе к входному вектору
  3. Увеличивать и повторите, начиная с шага 2, пока

Инициализация SOM

Выбор хорошего начального приближения - известная проблема для всех итерационных методов обучения нейронных сетей. Кохонен[13] использовали случайное инициирование весов SOM. В последнее время инициализация главных компонентов, при которой начальные веса карты выбираются из пространства первых главных компонент, стала популярной из-за точной воспроизводимости результатов.[14]

Тщательное сравнение подхода случайного инициирования к инициализации главного компонента для одномерного SOM (модели главных кривых) показало, что преимущества инициализации главного компонента SOM не универсальны. Лучший способ инициализации зависит от геометрии конкретного набора данных. Инициализация главного компонента предпочтительнее (в измерении один), если главная кривая, аппроксимирующая набор данных, может быть однолистно и линейно спроецирована на первый главный компонент (квазилинейные множества). Однако для нелинейных наборов данных случайное инициирование работает лучше.[15]

Примеры

Данные цветка ириса Фишера

Рассмотрим п×м массив узлов, каждый из которых содержит вектор весов и знает свое местоположение в массиве. Каждый весовой вектор имеет ту же размерность, что и входной вектор узла. Первоначально веса могут быть установлены на случайные значения.

Теперь нам нужен ввод для подачи карты. Цвета могут быть представлены их красными, зелеными и синими компонентами. Следовательно, мы будем представлять цвета как векторы в единичный куб из свободное векторное пространство над ℝ генерируется базисом:

R = <255, 0, 0>
G = <0, 255, 0>
B = <0, 0, 255>

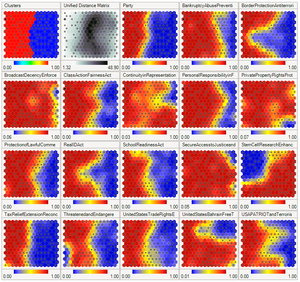
Показанная диаграмма

Самоорганизующиеся карты (SOM) трех и восьми цветов с U-Matrix.

сравнивает результаты обучения на наборах данных[Примечание 1]

threeColors = [255, 0, 0], [0, 255, 0], [0, 0, 255]
восемьColors = [0, 0, 0], [255, 0, 0], [0, 255, 0], [0, 0, 255], [255, 255, 0], [0, 255, 255], [255, 0, 255], [255, 255, 255]

и исходные изображения. Обратите внимание на поразительное сходство между ними.

Точно так же после тренировки 40×40 сетка нейронов на 250 итераций с скорость обучения 0,1 на Ирис Фишера, на карте уже можно обнаружить основные различия между видами.

Самоорганизующаяся карта (SOM) набора данных Fisher's Iris Flower с U-Matrix. Вверху слева: цветное изображение, сформированное первыми тремя измерениями четырехмерных весовых векторов SOM. Вверху справа: псевдоцветное изображение величины весовых векторов SOM. Внизу слева: U-матрица (евклидово расстояние между весовыми векторами соседних ячеек) SOM. Внизу справа: наложение точек данных (красный: I. setosa, зеленый: I. разноцветный и синий: I. virginica) на U-матрице на основе минимального евклидова расстояния между векторами данных и весовыми векторами SOM.

Интерпретация

Картографическое представление самоорганизующейся карты (U-матрица ) на основе данных о избранных статьях Википедии (частота слов). Расстояние обратно пропорционально сходству. «Горы» - это грани между кластерами. Красные линии - это ссылки между статьями.
Сравнение одномерного SOM и анализа главных компонентов (PCA) для аппроксимации данных. SOM - красный пунктирная линия с квадратами, 20 узлов. Первый главный компонент представлен синей линией. Точки данных - это маленькие серые кружки. Для PCA доля необъяснимой дисперсии в этом примере - 23,23%, для SOM - 6,86%.[16]

Есть два способа интерпретировать SOM. Поскольку на этапе обучения веса всего окружения перемещаются в одном направлении, похожие предметы имеют тенденцию возбуждать соседние нейроны. Таким образом, SOM формирует семантическую карту, в которой похожие образцы отображаются близко друг к другу, а несходные - отдельно. Это может быть визуализировано U-матрица (Евклидово расстояние между весовыми векторами соседних ячеек) SOM.[5][6][17]

Другой способ - рассматривать веса нейронов как указатели на входное пространство. Они образуют дискретную аппроксимацию распределения обучающих выборок. Больше нейронов указывает на области с высокой концентрацией обучающей выборки и меньше нейронов, где выборок мало.

SOM можно рассматривать как нелинейное обобщение Анализ основных компонентов (СПС).[18] На искусственных и реальных геофизических данных было показано, что ПОВ имеет много преимуществ.[19][20] по сравнению с обычным извлечение признаков такие методы, как эмпирические ортогональные функции (EOF) или PCA.

Первоначально SOM не был сформулирован как решение проблемы оптимизации. Тем не менее, было несколько попыток изменить определение SOM и сформулировать проблему оптимизации, которая дает аналогичные результаты.[21] Например, Эластичные карты использовать механическую метафору эластичности, чтобы приблизить главные многообразия:[22] аналогия - эластичная мембрана и пластина.

Альтернативы

  • В генеративная топографическая карта (GTM) - потенциальная альтернатива SOM. В том смысле, что GTM явно требует гладкого и непрерывного отображения из пространства ввода в пространство карты, он сохраняет топологию. Однако в практическом смысле этой меры топологической сохранности нет.[23]
  • В адаптивная ко времени самоорганизующаяся карта (TASOM) сеть является расширением базового SOM. TASOM использует адаптивную скорость обучения и функции соседства. Он также включает параметр масштабирования, чтобы сделать сеть инвариантной к масштабированию, перемещению и вращению входного пространства. TASOM и его варианты использовались в нескольких приложениях, включая адаптивную кластеризацию, многоуровневую пороговую обработку, аппроксимацию входного пространства и моделирование активного контура.[24] Более того, было предложено двоичное дерево TASOM или BTASOM, напоминающее двоичное естественное дерево, имеющее узлы, состоящие из сетей TASOM, где количество его уровней и количество его узлов адаптируются к его среде.[25]
  • В растущая самоорганизующаяся карта (ВШМ) - развивающийся вариант самоорганизующейся карты. ВШМ была разработана для решения проблемы определения подходящего размера карты в ЗВОЛ. Он начинается с минимального количества узлов (обычно четырех) и наращивает новые узлы на границе на основе эвристики. Используя значение, называемое коэффициент распространения, аналитик данных имеет возможность контролировать рост GSOM.
  • В эластичные карты подход[26] заимствует у сплайн-интерполяция идея минимизации упругая энергия. При обучении сводится к минимуму сумма квадратичной энергии изгиба и растяжения с наименьших квадратов ошибка приближения.
  • Конформный подход [27][28] который использует конформное отображение для интерполяции каждой обучающей выборки между узлами сетки на непрерывной поверхности. При таком подходе возможно однозначное сглаживание.
  • В ориентированная и масштабируемая карта (OS-Map) обобщает функцию соседства и выбор победителя.[29] Однородная гауссова функция окрестности заменяется матричной экспонентой. Таким образом, можно указать ориентацию либо в пространстве карты, либо в пространстве данных. SOM имеет фиксированный масштаб (= 1), так что карты «оптимально описывают область наблюдения». Но как насчет карты, покрывающей область дважды или n-кратно? Это влечет за собой концепцию масштабирования. OS-Map рассматривает масштаб как статистическое описание того, сколько узлов наилучшим образом соответствует входным данным на карте.

Приложения

Смотрите также

Примечания

  1. ^ Эти наборы данных не нормализованный. Для обучения SOM потребуется нормализация.

Рекомендации

  1. ^ Кохонен, Теуво; Хонкела, Тимо (2007). "Сеть Кохонена". Scholarpedia. 2 (1): 1568. Bibcode:2007SchpJ ... 2,1568K. Дои:10.4249 / scholarpedia.1568.
  2. ^ Кохонен, Теуво (1982). «Самоорганизованное формирование топологически корректных карт признаков». Биологическая кибернетика. 43 (1): 59–69. Дои:10.1007 / bf00337288. S2CID  206775459.
  3. ^ Фон дер Мальсбург, К. (1973). «Самоорганизация ориентировочно чувствительных клеток в полосатой коре головного мозга». Кибернетик. 14 (2): 85–100. Дои:10.1007 / bf00288907. PMID  4786750. S2CID  3351573.
  4. ^ Тьюринг, Алан (1952). «Химические основы морфогенеза». Фил. Пер. Р. Соц. 237 (641): 37–72. Bibcode:1952РСПТБ.237 ... 37Т. Дои:10.1098 / рстб.1952.0012.
  5. ^ а б Ульч, Альфред; Симон, Х. Питер (1990). «Самоорганизующиеся карты функций Кохонена для исследовательского анализа данных». В Видроу, Бернард; Angeniol, Bernard (ред.). Труды Международной конференции по нейронным сетям (INNC-90), Париж, Франция, 9–13 июля 1990 г.. 1. Дордрехт, Нидерланды: Kluwer. стр.305–308. ISBN  978-0-7923-0831-7.
  6. ^ а б Ульч, Альфред (2003); U * -Matrix: инструмент для визуализации кластеров в данных большой размерности, Факультет компьютерных наук Марбургского университета, Технический отчет № 36: 1-12
  7. ^ Ульч, Альфред (2007). «Появление в самоорганизующихся картах признаков». В Ritter, H .; Haschke, R. (ред.). Материалы 6-го международного семинара по самоорганизующимся картам (WSOM '07). Билефельд, Германия: Группа нейроинформатики. ISBN  978-3-00-022473-7.
  8. ^ Яакко Холлмен (9 марта 1996 г.). «Самоорганизующаяся карта (SOM)». Университет Аалто.
  9. ^ а б Хайкин, Саймон (1999). «9. Самоорганизующиеся карты». Нейронные сети - исчерпывающий фундамент (2-е изд.). Прентис-Холл. ISBN  978-0-13-908385-3.
  10. ^ Кохонен, Теуво (2005). «Введение в SOM». Набор инструментов SOM. Получено 2006-06-18.
  11. ^ Кохонен, Теуво; Хонкела, Тимо (2011). «Сеть Кохонена». Scholarpedia. 2: 1568. Bibcode:2007SchpJ ... 2,1568K. Дои:10.4249 / scholarpedia.1568. Получено 2012-09-24.
  12. ^ Вризе, О. (1995). "Сеть Кохонена" (PDF). Искусственные нейронные сети. Springer. Конспект лекций по информатике. 931. Лимбургский университет, Маастрихт. С. 83–100. Дои:10.1007 / BFb0027024. ISBN  978-3-540-59488-8. Получено 1 июля 2020.
  13. ^ Т. Кохонен, Самоорганизация и ассоциативная память. Спрингер, Берлин, 1984.
  14. ^ А. Чампи, Ю. Лешевалье, Кластеризация больших многоуровневых наборов данных: подход, основанный на самоорганизующихся картах Кохонена, в Д.А. Zighed, J. Komorowski, J. Zytkow (Eds.), PKDD 2000, Springer LNCS (LNAI), т. 1910, стр. 353-358, 2000.
  15. ^ Акиндуко, А.А .; Mirkes, E.M .; Горбань, А. (2016). «SOM: стохастическая инициализация по сравнению с основными компонентами». Информационные науки. 364–365: 213–221. Дои:10.1016 / j.ins.2015.10.013.
  16. ^ Иллюстрация подготовлена ​​с использованием бесплатного программного обеспечения: Mirkes, Evgeny M .; Анализ основных компонентов и самоорганизующиеся карты: апплет, Университет Лестера, 2011 г.
  17. ^ Саадатдуст, Робаб, Алекс Цзе Хианг Сим и Джафаркарими, Хосейн. «Применение самоорганизующейся карты для открытия знаний на основе данных высшего образования». Исследования и инновации в информационных системах (ICRIIS), Международная конференция 2011 г. IEEE, 2011.
  18. ^ Инь, Худжунь; Изучение нелинейных главных многообразий с помощью самоорганизующихся карт, в Горбань Александр Николаевич; Кегл, Балаж; Wunsch, Donald C .; и Зиновьев, Андрей (ред.); Основные многообразия для визуализации данных и уменьшения размерности, Конспект лекций по информатике и инженерии (LNCSE), т. 58, Берлин, Германия: Springer, 2008 г., ISBN  978-3-540-73749-0
  19. ^ Лю, Юнган; Вайсберг, Роберт Х (2005). «Паттерны изменчивости океанских течений на шельфе Западной Флориды с использованием самоорганизующейся карты». Журнал геофизических исследований. 110 (C6): C06003. Bibcode:2005JGRC..110.6003L. Дои:10.1029 / 2004JC002786.
  20. ^ Лю, Юнган; Вайсберг, Роберт Х .; Муерс, Кристофер Н. К. (2006). «Оценка производительности самоорганизующейся карты для извлечения признаков». Журнал геофизических исследований. 111 (C5): C05018. Bibcode:2006JGRC..111.5018L. Дои:10.1029 / 2005jc003117.
  21. ^ Хескес, Том; Энергетические функции для самоорганизующихся карт в Оя, Эркки; и Каски, Самуэль (ред.), Карты Кохонена, Эльзевир, 1999
  22. ^ Горбань Александр Николаевич; Кегл, Балаж; Wunsch, Donald C .; и Зиновьев, Андрей (ред.); Основные многообразия для визуализации данных и уменьшения размерности, Конспект лекций по информатике и инженерии (LNCSE), т. 58, Берлин, Германия: Springer, 2008 г., ISBN  978-3-540-73749-0
  23. ^ Каски, Самуэль (1997). Исследование данных с помощью самоорганизующихся карт. Acta Polytechnica Scandinavica. Математика, вычисления и менеджмент в инженерии. Серия № 82. Эспоо, Финляндия: Финская технологическая академия. ISBN  978-952-5148-13-8.
  24. ^ Шах-Хоссейни, Хамед; Сафабахш, Реза (апрель 2003 г.). «ТАСОМ: Самоорганизующаяся карта, адаптивная к новому времени». Транзакции IEEE по системам, человеку и кибернетике - Часть B: Кибернетика. 33 (2): 271–282. Дои:10.1109 / tsmcb.2003.810442. PMID  18238177.
  25. ^ Шах-Хоссейни, Хамед (май 2011 г.). "Двоичное дерево Адаптивная самоорганизующаяся карта времени". Нейрокомпьютинг. 74 (11): 1823–1839. Дои:10.1016 / j.neucom.2010.07.037.
  26. ^ А. Н. Горбань, А. Зиновьев, Основные многообразия и графы на практике: от молекулярной биологии к динамическим системам, Международный журнал нейронных систем, Vol. 20, № 3 (2010) 219–232.
  27. ^ Liou, C.-Y .; Куо, Ю.-Т. (2005). «Конформная самоорганизующаяся карта для многообразия нулевого рода». Визуальный компьютер. 21 (5): 340–353. Дои:10.1007 / s00371-005-0290-6. S2CID  8677589.
  28. ^ Liou, C.-Y .; Тай, В.-П. (2000). «Конформность в сети самоорганизации». Искусственный интеллект. 116 (1–2): 265–286. Дои:10.1016 / S0004-3702 (99) 00093-4.
  29. ^ Хуа, Х (2016). «Обработка изображений и геометрии с помощью ориентированной и масштабируемой карты». Нейронные сети. 77: 1–6. Дои:10.1016 / j.neunet.2016.01.009. PMID  26897100.
  30. ^ Чжэн, Г. и Вайшнави, В. (2011) «Подход с использованием многомерной карты восприятия для определения приоритетов и выбора проекта», Транзакции AIS о взаимодействии человека и компьютера (3) 2, стр. 82-103
  31. ^ Taner, M. T .; Walls, J.D .; Smith, M .; Taylor, G .; Carr, M. B .; Дюма, Д. (2001). «Характеристика коллектора путем калибровки самоорганизованных кластеров карт». Расширенные тезисы технической программы SEG 2001. 2001. С. 1552–1555. Дои:10.1190/1.1816406. S2CID  59155082.
  32. ^ Чанг, Вуи Ли; Панг, Ли Мэн; Тай, Кай Мэн (март 2017 г.). «Применение самоорганизующейся карты к методологии анализа видов и последствий отказов» (PDF). Нейрокомпьютинг. PP: 314–320. Дои:10.1016 / j.neucom.2016.04.073.
  33. ^ ANNetGPGPU CUDA Library с примерами [1] Создание изображений с ускорением на GPU