Танграм - Tangram

В Танграм (Китайский : 七巧板; пиньинь : qīqiǎobǎn; горит 'семь досок мастерства') загадка рассечения состоящий из семи плоских многоугольников, называемых загар, которые складываются в фигуры. Цель состоит в том, чтобы воспроизвести шаблон (только набросок), обычно встречающийся в сборнике головоломок, с использованием всех семи частей без наложения. В качестве альтернативы загар могут использоваться для создания оригинальных минималистичных дизайнов, которые ценятся либо за присущие им эстетические достоинства, либо как основа для побуждения других воспроизвести его очертания. Считается, что он был изобретен в Китай где-то в конце 18 века н.э., а затем перенесены в Америка и Европа продавая корабли вскоре после этого.[1] Некоторое время он стал очень популярным в Европе, а затем снова во время Первая Мировая Война. Это одна из наиболее широко известных головоломок в мире, которая использовалась для различных целей, включая развлечения, искусство и образование.[2][3]
Этимология
Происхождение слова «танграм» неясно. Согласно одной из гипотез, это соединение греческого элемента «-грамма», образованного от γράμμα ('письменный символ, буква, то, что нарисовано') с элементом 'tan-', который, по разным предположениям, является китайским Тан 'расширять' или кантонский Тан 'Китайский'.[4] С другой стороны, это слово может быть производным от архаичного английского «trangram», означающего «странная, замысловато надуманная вещь».[5]
В любом случае считается, что первое известное употребление этого слова было найдено в книге 1848 года. Геометрическая головоломка для юношества математик и будущий президент Гарвардского университета Томас Хилл который, вероятно, ввел этот термин в одно и то же произведение. Хилл активно продвигал это слово в многочисленных статьях, пропагандирующих использование головоломки в образовании, и в 1864 году она получила официальное признание на английском языке, когда была включена в книгу Ноя Вебстера. Американский словарь.[6]
История
Происхождение
Первые годы попыток датировать Танграм были смущены популярной, но обманным путем написанной историей знаменитого создателя головоломок. Сэмюэл Лойд в его 1908 Восьмая книга загара. Эта работа содержит много причудливых особенностей, которые вызвали как интерес, так и подозрение среди современных ученых, которые пытались проверить отчет. К 1910 году стало ясно, что это розыгрыш. Письмо этого года от Оксфордский словарь редактор Сэр Джеймс Мюррей от имени ряда китайских ученых выдающемуся загадочному списку Генри Дудени гласит: «В результате было показано, что человек Тан, бог Тан и Книга Тан полностью неизвестны китайской литературе, истории или традициям». [7] Наряду с множеством странных деталей Восьмая книга Тана дату создания загадки 4000 лет в древности нужно было считать совершенно необоснованной и ложной.
Исторический китайский изобретатель Танграма неизвестен, кроме как под псевдонимом Ян-чо-чу-ши (Тупой отшельник). Считается, что загадка была впервые представлена в книге под названием Чи цзиао ту который уже упоминался как потерянный в 1815 году Шань-цзяо в своей книге Новые фигуры Танграма. Тем не менее, обычно считается, что загадка возникла примерно на 20 лет раньше, чем это. [8]
Несмотря на его относительно недавнее создание, в Китае существует гораздо более древняя традиция анекдотов, которая, вероятно, сыграла роль в их создании. В частности, модульные банкетные столы династии Сун имеют странное сходство с игровыми элементами Танграма, и были книги, посвященные их расположению вместе, чтобы сформировать приятные узоры.[9]
Выдающийся математик III века Лю Хуэй в своих работах использовал доказательства конструкции, и некоторые из них имеют поразительное сходство с впоследствии разработанными банкетными столами, которые, в свою очередь, похоже, предвосхищают Танграм. Хотя нет причин подозревать, что танграммы использовались для доказательства теорема Пифагора, как иногда сообщается, вполне вероятно, что этот стиль геометрических рассуждений оказал влияние на китайскую культурную жизнь, что привело непосредственно к загадке.[10]
Выход в западный мир (1815–1820-е гг.)

Самый ранний из сохранившихся танграмов был подарен филадельфийскому морскому магнату и конгрессмену Фрэнсису Уолну в 1802 году, но западная аудитория в целом столкнулась с загадкой только через десять лет. [11] В 1815 году американскому капитану М. Донналдсону подарили пару книг автора Санг-Ся-кои по этому предмету (одна проблема и одна книга решений), когда его корабль, Трейдер состыковался там. Затем они были доставлены на корабле в Филадельфию в феврале 1816 года. Первая книга по танграму, изданная в Америке, была основана на паре, привезенной Донналдсоном.[12]
В конце концов головоломка достигла Англии, где стала очень модной. Повальное увлечение быстро распространилось на другие европейские страны. В основном это произошло из-за пары британских книг по танграму, Модная китайская головоломка, и прилагаемую книгу решений, Ключ.[13] Вскоре наборы танграм в большом количестве экспортировались из Китая, сделанные из различных материалов, от стекла до дерева и панциря черепахи.[14]
Многие из этих необычных и изысканных наборов танграм попали в Дания. Интерес к танграмам в Дании резко возрос примерно в 1818 году, когда были опубликованы две книги по головоломке, вызвавшие большой энтузиазм.[15] Первым из них был Мандаринский (О китайской игре). Это написал студент Копенгагенский университет, который был научно-популярным произведением об истории и популярности танграмов. Секунда, Det nye chinesiske Gaadespil (Новая китайская игра-головоломка), состоящая из 339 головоломок, скопированных с Восьмая книга загара, а также один оригинал.[15]
Одним из факторов, способствовавших популярности игры в Европе, было то, что хотя католическая церковь запретили многие формы отдыха в субботу, они не возражали против головоломок, таких как танграм.[16]
Второе увлечение в Германии (1891–1920-е годы)
Впервые танграммы были представлены немецкой публике промышленником Фридрих Адольф Рихтер около 1891 г.[17] Наборы были каменные или фальшивые. глиняная посуда,[18] и продается под названием «Якорная головоломка».[17]
В международном масштабе, Первая мировая война вызвала большой всплеск интереса к танграмам в тылу и в окопах обеих сторон. В это время он иногда носил название "The Сфинкс »альтернативное название для наборов« Якорная головоломка ».[19][20]
Парадоксы

На рисунке 1 длины сторон обозначены в предположении, что стороны квадрата равны единице.
На рисунке 2 наложение тел показывает, что безногий корпус больше на площадь ступни. Изменение площади часто остается незамеченным, поскольку √2 близко к 1,5.
Танграм парадокс - это ошибка рассечения: две фигуры составлены из одного и того же набора частей, одна из которых кажется правильным подмножеством другой.[21] Один известный парадокс - это парадокс двух монахи, приписываемый Dudeney, который состоит из двух одинаковых фигур, у одной из которых нет ступни.[22] На самом деле площадь стопы на втором рисунке компенсируется чуть большим телом. Другой парадокс танграма предложен Сэм Лойд в 8-я книга загара:[23]
Седьмая и восьмая фигуры представляют собой таинственный квадрат, состоящий из семи частей: затем с отрезанным углом, но все те же семь частей.[24]
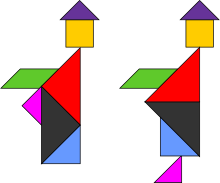
Парадокс двух монахов - две похожие фигуры, но у одного отсутствует ступня:
Парадокс танграма Magic Dice Cup - из книги Сэма Лойда Восьмая книга загара[25] (1903). Каждая из этих чашек состояла из семи геометрических фигур. Но первая чашка целая, а в других есть вакансии разного размера. (Обратите внимание, что один слева немного короче двух других. Один в середине чуть-чуть шире, чем справа, а тот, что слева, еще уже.)[26]

Парадокс обрезанного квадратного танграма - из книги Лойда Восьмая книга загара[25] (1903):
Количество конфигураций

Только из текстов XIX века было создано более 6500 различных задач танграма, и в настоящее время их число постоянно растет.[27] Фу Трейнг Ван и Чуан-Чин Сюн доказали в 1942 году, что их всего тринадцать. выпуклый Конфигурации tangram (сегмент конфигурации, нарисованный между любыми двумя точками на краю конфигурации, всегда проходит через внутреннюю часть конфигурации, то есть конфигурации без углублений в контуре).[28][29]
Шт
Выбирая единицу измерения так, чтобы семь частей могли быть собраны в квадрат со стороной одна единица и площадью 1 квадратная единица, семь частей:[30]
- 2 больших прямоугольные треугольники (гипотенуза 1, стороны √2/2, площадь 1/4)
- 1 средний прямоугольный треугольник (гипотенуза √2/2, стороны 1/2, площадь 1/8)
- 2 маленьких прямоугольных треугольника (гипотенуза 1/2, стороны √2/4, площадь 1/16)
- 1 квадрат (стороны √2/4, площадь 1/8)
- 1 параллелограмм (стороны 1/2 и √2/4, высота 1/4, площадь 1/8)
Из этих семи частей параллелограмм уникален тем, что у него нет симметрия отражения но только вращательная симметрия, и поэтому его зеркальное отражение можно получить, только перевернув его. Таким образом, это единственная деталь, которую может потребоваться перевернуть при формировании определенных форм.
Смотрите также
использованная литература
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 21. ISBN 9781402704130.
- ^ Слокум, Джерри (2001). Дао Танграма. Barnes & Noble. п. 9. ISBN 978-1-4351-0156-2.CS1 maint: ref = harv (ссылка на сайт)
- ^ Форбраш, Уильям Байрон (1914). Руководство игры. Джейкобс. п. 315. Получено 2010-10-13.
- ^ Оксфордский словарь английского языка, 1910, s.v.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 23. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 25. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 23. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 16-19. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 16. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 15. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 21. ISBN 9781402704130.
- ^ Слокум, Джерри (2003). Книга Танграма. Стерлинг. п. 30. ISBN 9781402704130.
- ^ Слокум (2003), п. 31)
- ^ Слокум (2003), п. 49)
- ^ а б Слокум (2003), стр. 99–100).
- ^ Слокум (2003), п. 51)
- ^ а б Waeber, Sarcone &. «Танграм - невероятная вечная« китайская »головоломка 2». www.archimedes-lab.org.
- ^ Решения казначейства в соответствии с таможенным и другим законодательством, Том 25. Министерство финансов США. 1890–1926 гг. п. 1421. Получено 16 сентября, 2010.
- ^ Вятт (26 апреля 2006 г.). «Танграм - китайская головоломка». BBC. Получено 3 октября 2010.
- ^ Браман, Арлетт (2002). Дети со всего мира играют!. Джон Уайли и сыновья. п. 10. ISBN 978-0-471-40984-7. Получено 5 сентября, 2010.
- ^ Танграм Парадокс, Барил, Маргарита, From MathWorld - веб-ресурс Wolfram, созданный Эриком В. Вайсттайном.
- ^ Дудени, Х. (1958). Развлечения по математике. Нью-Йорк: Dover Publications.
- ^ 8-я книга загара (1903).
- ^ Лойд, Сэм (1968). Восьмая книга Тан - 700 Танграмов Сэма Лойда с введением и решениями Питера Ван Нота. Нью-Йорк: Dover Publications. п. 25.
- ^ а б Восьмая книга загара, Страница 1
- ^ "Волшебный кубок". 2 апреля 2011 г.
- ^ Слокум (2001), п. 37)
- ^ Фу Трейнг Ван; Чуан-Чжи Сюн (ноябрь 1942 г.). «Теорема о Танграме». Американский математический ежемесячник. 49 (9): 596–599. Дои:10.2307/2303340. JSTOR 2303340.
- ^ Прочтите, Рональд К. (1965). Танграммы: 330 головоломок. Нью-Йорк: Dover Publications. п. 53. ISBN 0-486-21483-4.
- ^ Брукс, Дэвид Дж. (2018-12-01). «Как сделать классическую головоломку Tangram». Журнал Boys 'Life. Получено 2020-03-10.
дальнейшее чтение
- Анно, Мицумаса. Математические игры Anno (три тома). Нью-Йорк: Philomel Books, 1987. ISBN 0-399-21151-9 (v. 1), ISBN 0-698-11672-0 (v. 2), ISBN 0-399-22274-X (т. 3).
- Ботерманс, Джек и др. Мир игр: их происхождение и история, как в них играть и как их создавать (перевод Wereld vol spelletjes). Нью-Йорк: факты в архиве, 1989. ISBN 0-8160-2184-8.
- Дудени, Х. Развлечения по математике. Нью-Йорк: Dover Publications, 1958.
- Гарднер, Мартин. "Математические игры - о фантастической истории и творческих задачах головоломки Танграм", Scientific American Август 1974 г., стр. 98–103.
- Гарднер, Мартин. "Подробнее о Tangrams", Scientific American Сентябрь 1974 г., стр. 187–191.
- Гарднер, Мартин. 2-я книга по математическим головоломкам и решениям журнала Scientific American. Нью-Йорк: Саймон и Шустер, 1961. ISBN 0-671-24559-7.
- Лойд, Сэм. Книга загадок Сэма Лойда Танграма (8-я книга Танграма, часть I). Минеола, Нью-Йорк: Dover Publications, 1968.
- Слокум, Джерри и др. Старые и новые загадки: как их собирать и решать. Де Меерн, Нидерланды: Plenary Publications International (Европа); Амстердам, Нидерланды: ADM International; Сиэтл: Распространено Вашингтонским университетом, 1986. ISBN 0-295-96350-6.
