В математика , векторные сферические гармоники (VSH ) являются продолжением скаляра сферические гармоники для использования с векторные поля . Компоненты VSH: комплексный функции, выраженные в базисные векторы в сферических координатах .
Определение Для определения VSH использовалось несколько соглашений.[1] [2] [3] [4] [5] и другие. . Учитывая скаляр сферическая гармоника Ylm (θ , φ )
Y л м = Y л м р ^ , {displaystyle mathbf {Y} _ {lm} = Y_ {lm} {hat {mathbf {r}}},} Ψ л м = р ∇ Y л м , {displaystyle mathbf {Psi} _ {lm} = rabla Y_ {lm},} Φ л м = р × ∇ Y л м , {displaystyle mathbf {Phi} _ {lm} = mathbf {r} imes abla Y_ {lm},} с р ^ {displaystyle {шляпа {mathbf {r}}}} единичный вектор в радиальном направлении в сферические координаты и р {displaystyle mathbf {r}} р = р р ^ {displaystyle mathbf {r} = r {hat {mathbf {r}}}}
Интерес этих новых векторных полей состоит в том, чтобы отделить радиальную зависимость от угловой при использовании сферических координат, так что векторное поле допускает мультипольное расширение
E = ∑ л = 0 ∞ ∑ м = − л л ( E л м р ( р ) Y л м + E л м ( 1 ) ( р ) Ψ л м + E л м ( 2 ) ( р ) Φ л м ) . {displaystyle mathbf {E} = sum _ {l = 0} ^ {infty} sum _ {m = -l} ^ {l} left (E_ {lm} ^ {r} (r) mathbf {Y} _ {lm } + E_ {lm} ^ {(1)} (r) mathbf {Psi} _ {lm} + E_ {lm} ^ {(2)} (r) mathbf {Phi} _ {lm} ight).} Метки на компонентах отражают это E л м р {displaystyle E_ {lm} ^ {r}} E л м ( 1 ) {displaystyle E_ {lm} ^ {(1)}} E л м ( 2 ) {displaystyle E_ {lm} ^ {(2)}} р {displaystyle mathbf {r}}
Основные свойства Симметрия Как и скалярные сферические гармоники, VSH удовлетворяет
Y л , − м = ( − 1 ) м Y л м ∗ , Ψ л , − м = ( − 1 ) м Ψ л м ∗ , Φ л , − м = ( − 1 ) м Φ л м ∗ , {displaystyle {egin {align} mathbf {Y} _ {l, -m} & = (- 1) ^ {m} mathbf {Y} _ {lm} ^ {*}, mathbf {Psi} _ {l, -m} & = (- 1) ^ {m} mathbf {Psi} _ {lm} ^ {*}, mathbf {Phi} _ {l, -m} & = (- 1) ^ {m} mathbf { Phi} _ {lm} ^ {*}, конец {выровнен}}} что сокращает количество независимых функций примерно вдвое. Звездочка указывает комплексное сопряжение .
Ортогональность VSH являются ортогональный обычным трехмерным способом в каждой точке р {displaystyle mathbf {r}}
Y л м ( р ) ⋅ Ψ л м ( р ) = 0 , Y л м ( р ) ⋅ Φ л м ( р ) = 0 , Ψ л м ( р ) ⋅ Φ л м ( р ) = 0. {displaystyle {egin {align} mathbf {Y} _ {lm} (mathbf {r}) cdot mathbf {Psi} _ {lm} (mathbf {r}) & = 0, mathbf {Y} _ {lm} ( mathbf {r}) cdot mathbf {Phi} _ {lm} (mathbf {r}) & = 0, mathbf {Psi} _ {lm} (mathbf {r}) cdot mathbf {Phi} _ {lm} (mathbf {r}) & = 0.end {выровнено}}} Они также ортогональны в гильбертовом пространстве:
∫ Y л м ⋅ Y л ′ м ′ ∗ d Ω = δ л л ′ δ м м ′ , ∫ Ψ л м ⋅ Ψ л ′ м ′ ∗ d Ω = л ( л + 1 ) δ л л ′ δ м м ′ , ∫ Φ л м ⋅ Φ л ′ м ′ ∗ d Ω = л ( л + 1 ) δ л л ′ δ м м ′ , ∫ Y л м ⋅ Ψ л ′ м ′ ∗ d Ω = 0 , ∫ Y л м ⋅ Φ л ′ м ′ ∗ d Ω = 0 , ∫ Ψ л м ⋅ Φ л ′ м ′ ∗ d Ω = 0. {displaystyle {egin {выравнивается} int mathbf {Y} _ {lm} cdot mathbf {Y} _ {l'm '} ^ {*}, dOmega & = delta _ {ll'} delta _ {mm '}, int mathbf {Psi} _ {lm} cdot mathbf {Psi} _ {l'm '} ^ {*}, dOmega & = l (l + 1) delta _ {ll'} delta _ {mm '}, int mathbf {Phi} _ {lm} cdot mathbf {Phi} _ {l'm '} ^ {*}, dOmega & = l (l + 1) delta _ {ll'} delta _ {mm '}, int mathbf {Y} _ {lm} cdot mathbf {Psi} _ {l'm '} ^ {*}, dOmega & = 0, int mathbf {Y} _ {lm} cdot mathbf {Phi} _ {l'm' } ^ {*}, dOmega & = 0, int mathbf {Psi} _ {lm} cdot mathbf {Phi} _ {l'm '} ^ {*}, dOmega & = 0.end {выровнено}}} Дополнительный результат в одной точке р {displaystyle mathbf {r}} л , м , л ′ , м ′ {displaystyle l, m, l ', m'}
Y л м ( р ) ⋅ Ψ л ′ м ′ ( р ) = 0 , Y л м ( р ) ⋅ Φ л ′ м ′ ( р ) = 0. {displaystyle {egin {align} mathbf {Y} _ {lm} (mathbf {r}) cdot mathbf {Psi} _ {l'm '} (mathbf {r}) & = 0, mathbf {Y} _ { lm} (mathbf {r}) cdot mathbf {Phi} _ {l'm '} (mathbf {r}) & = 0.end {выровнено}}} Векторные мультипольные моменты Соотношения ортогональности позволяют вычислить сферические мультипольные моменты векторного поля как
E л м р = ∫ E ⋅ Y л м ∗ d Ω , E л м ( 1 ) = 1 л ( л + 1 ) ∫ E ⋅ Ψ л м ∗ d Ω , E л м ( 2 ) = 1 л ( л + 1 ) ∫ E ⋅ Φ л м ∗ d Ω . {displaystyle {egin {align} E_ {lm} ^ {r} & = int mathbf {E} cdot mathbf {Y} _ {lm} ^ {*}, dOmega, E_ {lm} ^ {(1)} & = {frac {1} {l (l + 1)}} int mathbf {E} cdot mathbf {Psi} _ {lm} ^ {*}, dOmega, E_ {lm} ^ {(2)} & = { frac {1} {l (l + 1)}} int mathbf {E} cdot mathbf {Phi} _ {lm} ^ {*}, dOmega .end {выровнено}}} Градиент скалярного поля Учитывая мультипольное расширение скалярного поля
ϕ = ∑ л = 0 ∞ ∑ м = − л л ϕ л м ( р ) Y л м ( θ , ϕ ) , {displaystyle phi = sum _ {l = 0} ^ {infty} sum _ {m = -l} ^ {l} phi _ {lm} (r) Y_ {lm} (heta, phi),} мы можем выразить его градиент через VSH как
∇ ϕ = ∑ л = 0 ∞ ∑ м = − л л ( d ϕ л м d р Y л м + ϕ л м р Ψ л м ) . {displaystyle abla phi = sum _ {l = 0} ^ {infty} sum _ {m = -l} ^ {l} left ({frac {dphi _ {lm}} {dr}} mathbf {Y} _ {lm } + {frac {phi _ {lm}} {r}} mathbf {Psi} _ {lm} ight).} Расхождение Для любого мультипольного поля имеем
∇ ⋅ ( ж ( р ) Y л м ) = ( d ж d р + 2 р ж ) Y л м , ∇ ⋅ ( ж ( р ) Ψ л м ) = − л ( л + 1 ) р ж Y л м , ∇ ⋅ ( ж ( р ) Φ л м ) = 0. {displaystyle {egin {выровнено} abla cdot left (f (r) mathbf {Y} _ {lm} ight) & = left ({frac {df} {dr}} + {frac {2} {r}} бой) Y_ {lm}, abla cdot left (f (r) mathbf {Psi} _ {lm} ight) & = - {frac {l (l + 1)} {r}} fY_ {lm}, abla cdot left (f (r) mathbf {Phi} _ {lm} ight) & = 0.end {выровнено}}} Путем суперпозиции получаем расхождение любого векторного поля:
∇ ⋅ E = ∑ л = 0 ∞ ∑ м = − л л ( d E л м р d р + 2 р E л м р − л ( л + 1 ) р E л м ( 1 ) ) Y л м . {displaystyle abla cdot mathbf {E} = sum _ {l = 0} ^ {infty} sum _ {m = -l} ^ {l} left ({frac {dE_ {lm} ^ {r}} {dr}} + {frac {2} {r}} E_ {lm} ^ {r} - {frac {l (l + 1)} {r}} E_ {lm} ^ {(1)} ight) Y_ {lm}. } Мы видим, что компонент на Φ lm соленоидный .
Завиток Для любого мультипольного поля имеем
∇ × ( ж ( р ) Y л м ) = − 1 р ж Φ л м , ∇ × ( ж ( р ) Ψ л м ) = ( d ж d р + 1 р ж ) Φ л м , ∇ × ( ж ( р ) Φ л м ) = − л ( л + 1 ) р ж Y л м − ( d ж d р + 1 р ж ) Ψ л м . {displaystyle {egin {align} abla imes left (f (r) mathbf {Y} _ {lm} ight) & = - {frac {1} {r}} fmathbf {Phi} _ {lm}, abla imes left (f (r) mathbf {Psi} _ {lm} ight) & = left ({frac {df} {dr}} + {frac {1} {r}} fight) mathbf {Phi} _ {lm}, abla imes left (f (r) mathbf {Phi} _ {lm} ight) & = - {frac {l (l + 1)} {r}} fmathbf {Y} _ {lm} -left ({frac {df } {dr}} + {frac {1} {r}} fight) mathbf {Psi} _ {lm} .end {выровнено}}} Путем суперпозиции получаем завиток любого векторного поля:
∇ × E = ∑ л = 0 ∞ ∑ м = − л л ( − л ( л + 1 ) р E л м ( 2 ) Y л м − ( d E л м ( 2 ) d р + 1 р E л м ( 2 ) ) Ψ л м + ( − 1 р E л м р + d E л м ( 1 ) d р + 1 р E л м ( 1 ) ) Φ л м ) . {displaystyle abla imes mathbf {E} = sum _ {l = 0} ^ {infty} sum _ {m = -l} ^ {l} left (- {frac {l (l + 1)} {r}} E_ {lm} ^ {(2)} mathbf {Y} _ {lm} -left ({frac {dE_ {lm} ^ {(2)}} {dr}} + {frac {1} {r}} E_ { lm} ^ {(2)} ight) mathbf {Psi} _ {lm} + left (- {frac {1} {r}} E_ {lm} ^ {r} + {frac {dE_ {lm} ^ {( 1)}} {dr}} + {frac {1} {r}} E_ {lm} ^ {(1)} ight) mathbf {Phi} _ {lm} ight).} Лапласиан Действие Оператор Лапласа Δ = ∇ ⋅ ∇ {displaystyle Delta = abla cdot abla}
Δ ( ж ( р ) Z л м ) = ( 1 р 2 ∂ ∂ р р 2 ∂ ж ∂ р ) Z л м + ж ( р ) Δ Z л м , {displaystyle Delta left (f (r) mathbf {Z} _ {lm} ight) = left ({frac {1} {r ^ {2}}} {frac {partial} {partial r}} r ^ {2}) {frac {partial f} {partial r}} ight) mathbf {Z} _ {lm} + f (r) Delta mathbf {Z} _ {lm},} куда Z л м = Y л м , Ψ л м , Φ л м {displaystyle mathbf {Z} _ {lm} = mathbf {Y} _ {lm}, mathbf {Psi} _ {lm}, mathbf {Phi} _ {lm}}
Δ Y л м = − 1 р 2 ( 2 + л ( л + 1 ) ) Y л м + 2 р 2 Ψ л м , Δ Ψ л м = 2 р 2 л ( л + 1 ) Y л м − 1 р 2 л ( л + 1 ) Ψ л м , Δ Φ л м = − 1 р 2 л ( л + 1 ) Φ л м . {displaystyle {egin {выравнивается} Delta mathbf {Y} _ {lm} & = - {frac {1} {r ^ {2}}} (2 + l (l + 1)) mathbf {Y} _ {lm} + {frac {2} {r ^ {2}}} mathbf {Psi} _ {lm}, Delta mathbf {Psi} _ {lm} & = {frac {2} {r ^ {2}}} l ( l + 1) mathbf {Y} _ {lm} - {frac {1} {r ^ {2}}} l (l + 1) mathbf {Psi} _ {lm}, Delta mathbf {Phi} _ {lm } & = - {frac {1} {r ^ {2}}} l (l + 1) mathbf {Phi} _ {lm} .end {выровнено}}} Также обратите внимание, что это действие становится симметричный , т.е. недиагональные коэффициенты равны 2 р 2 л ( л + 1 ) {displaystyle {frac {2} {r ^ {2}}} {sqrt {l (l + 1)}}} нормализованный VSH.
Примеры Первые векторные сферические гармоники л = 0 {displaystyle l = 0} Y 00 = 1 4 π р ^ , Ψ 00 = 0 , Φ 00 = 0 . {displaystyle {egin {align} mathbf {Y} _ {00} & = {sqrt {frac {1} {4pi}}} {hat {mathbf {r}}}, mathbf {Psi} _ {00} & = mathbf {0}, mathbf {Phi} _ {00} & = mathbf {0} .end {выровнено}}} л = 1 {displaystyle l = 1} Y 10 = 3 4 π потому что θ р ^ , Y 11 = − 3 8 π е я φ грех θ р ^ , {displaystyle {egin {выравнивается} mathbf {Y} _ {10} & = {sqrt {frac {3} {4pi}}} cos heta, {hat {mathbf {r}}}, mathbf {Y} _ {11 } & = - {sqrt {frac {3} {8pi}}} e ^ {ivarphi} sin heta, {hat {mathbf {r}}}, конец {выровнено}}} Ψ 10 = − 3 4 π грех θ θ ^ , Ψ 11 = − 3 8 π е я φ ( потому что θ θ ^ + я φ ^ ) , {displaystyle {egin {выравнивается} mathbf {Psi} _ {10} & = - {sqrt {frac {3} {4pi}}} sin heta, {hat {mathbf {heta}}}, mathbf {Psi} _ { 11} & = - {sqrt {frac {3} {8pi}}} e ^ {ivarphi} left (cos heta, {hat {mathbf {heta}}} + i, {hat {mathbf {varphi}}} ight) , конец {выровнен}}} Φ 10 = − 3 4 π грех θ φ ^ , Φ 11 = 3 8 π е я φ ( я θ ^ − потому что θ φ ^ ) . {displaystyle {egin {align} mathbf {Phi} _ {10} & = - {sqrt {frac {3} {4pi}}} sin heta, {hat {mathbf {varphi}}}, mathbf {Phi} _ { 11} & = {sqrt {frac {3} {8pi}}} e ^ {ivarphi} left (i, {hat {mathbf {heta}}} - cos heta, {hat {mathbf {varphi}}} ight). конец {выровнен}}} л = 2 {displaystyle l = 2} Y 20 = 1 4 5 π ( 3 потому что 2 θ − 1 ) р ^ , Y 21 = − 15 8 π грех θ потому что θ е я φ р ^ , Y 22 = 1 4 15 2 π грех 2 θ е 2 я φ р ^ . {displaystyle {egin {align} mathbf {Y} _ {20} & = {frac {1} {4}} {sqrt {frac {5} {pi}}}, (3cos ^ {2} heta -1), {hat {mathbf {r}}}, mathbf {Y} _ {21} & = - {sqrt {frac {15} {8pi}}}, sin heta, cos heta, e ^ {ivarphi}, {hat { mathbf {r}}}, mathbf {Y} _ {22} & = {frac {1} {4}} {sqrt {frac {15} {2pi}}}, sin ^ {2} heta, e ^ { 2ivarphi}, {шляпа {mathbf {r}}}. Конец {выровнено}}} Ψ 20 = − 3 2 5 π грех θ потому что θ θ ^ , Ψ 21 = − 15 8 π е я φ ( потому что 2 θ θ ^ + я потому что θ φ ^ ) , Ψ 22 = 15 8 π грех θ е 2 я φ ( потому что θ θ ^ + я φ ^ ) . {displaystyle {egin {выравнивается} mathbf {Psi} _ {20} & = - {frac {3} {2}} {sqrt {frac {5} {pi}}}, sin heta, cos heta, {hat {mathbf {heta}}}, mathbf {Psi} _ {21} & = - {sqrt {frac {15} {8pi}}}, e ^ {ivarphi}, left (cos 2 heta, {hat {mathbf {heta}) }} + icos heta, {hat {mathbf {varphi}}} ight), mathbf {Psi} _ {22} & = {sqrt {frac {15} {8pi}}}, sin heta, e ^ {2ivarphi} , left (cos heta, {hat {mathbf {heta}}} + i, {hat {mathbf {varphi}}} ight) .end {выровнено}}} Φ 20 = − 3 2 5 π грех θ потому что θ φ ^ , Φ 21 = 15 8 π е я φ ( я потому что θ θ ^ − потому что 2 θ φ ^ ) , Φ 22 = 15 8 π грех θ е 2 я φ ( − я θ ^ + потому что θ φ ^ ) . {displaystyle {egin {align} mathbf {Phi} _ {20} & = - {frac {3} {2}} {sqrt {frac {5} {pi}}} sin heta, cos heta, {hat {mathbf { varphi}}}, mathbf {Phi} _ {21} & = {sqrt {frac {15} {8pi}}}, e ^ {ivarphi}, слева (icos heta, {hat {mathbf {heta}}} - cos 2 heta, {hat {mathbf {varphi}}} ight), mathbf {Phi} _ {22} & = {sqrt {frac {15} {8pi}}}, sin heta, e ^ {2ivarphi}, слева (-i, {hat {mathbf {heta}}} + cos heta, {hat {mathbf {varphi}}} ight) .end {выровнено}}} Выражения для отрицательных значений м получаются применением соотношений симметрии.
Приложения Электродинамика VSH особенно полезны при изучении поля мультипольного излучения . Например, магнитный мультиполь возникает из-за колеблющегося тока с угловой частотой ω {displaystyle omega}
J ^ = J ( р ) Φ л м , {displaystyle {hat {mathbf {J}}} = J (r) mathbf {Phi} _ {lm},} и соответствующие электрическое и магнитное поля, можно записать как
E ^ = E ( р ) Φ л м , B ^ = B р ( р ) Y л м + B ( 1 ) ( р ) Ψ л м . {displaystyle {egin {align} {hat {mathbf {E}}} & = E (r) mathbf {Phi} _ {lm}, {hat {mathbf {B}}} & = B ^ {r} (r ) mathbf {Y} _ {lm} + B ^ {(1)} (r) mathbf {Psi} _ {lm} .end {выровнено}}} Подставляя в уравнения Максвелла, автоматически выполняется закон Гаусса
∇ ⋅ E ^ = 0 , {displaystyle abla cdot {hat {mathbf {E}}} = 0,} в то время как закон Фарадея разделяется как
∇ × E ^ = − я ω B ^ ⇒ { л ( л + 1 ) р E = я ω B р , d E d р + E р = я ω B ( 1 ) . {displaystyle abla imes {hat {mathbf {E}}} = - iomega {hat {mathbf {B}}} quad Rightarrow quad left {{egin {array} {l} displaystyle {frac {l (l + 1)} { r}} E = iomega B ^ {r}, displaystyle {frac {dE} {dr}} + {frac {E} {r}} = iomega B ^ {(1)}. end {array}} ight. } Из закона Гаусса для магнитного поля следует
∇ ⋅ B ^ = 0 ⇒ d B р d р + 2 р B р − л ( л + 1 ) р B ( 1 ) = 0 , {displaystyle abla cdot {hat {mathbf {B}}} = 0quad Rightarrow quad {frac {dB ^ {r}} {dr}} + {frac {2} {r}} B ^ {r} - {frac {l (l + 1)} {r}} B ^ {(1)} = 0,} а уравнение Ампера-Максвелла дает
∇ × B ^ = μ 0 J ^ + я μ 0 ε 0 ω E ^ ⇒ − B р р + d B ( 1 ) d р + B ( 1 ) р = μ 0 J + я ω μ 0 ε 0 E . {displaystyle abla imes {hat {mathbf {B}}} = mu _ {0} {hat {mathbf {J}}} + imu _ {0} varepsilon _ {0} omega {hat {mathbf {E}}} quad Четверка правой стрелки - {frac {B ^ {r}} {r}} + {frac {dB ^ {(1)}} {dr}} + {frac {B ^ {(1)}} {r}} = mu _ {0} J + iomega mu _ {0} varepsilon _ {0} E.} Таким образом, дифференциальные уравнения в частных производных были преобразованы в систему обыкновенных дифференциальных уравнений.
Альтернативное определение Угловая составляющая магнитных и электрических векторных сферических гармоник. Красные и зеленые стрелки показывают направление поля. Также представлены порождающие скалярные функции, показаны только первые три порядка (диполи, квадруполи, октуполи).
Во многих приложениях векторные сферические гармоники определяются как фундаментальный набор решений векторных Уравнение Гельмгольца в сферических координатах.[6] [7]
В этом случае векторные сферические гармоники порождаются скалярными функциями, которые являются решениями скалярного уравнения Гельмгольца с волновым вектором k {displaystyle {f {k}}}
ψ е м п = потому что м φ п п м ( потому что ϑ ) z п ( k р ) ψ о м п = грех м φ п п м ( потому что ϑ ) z п ( k р ) {displaystyle {egin {array} {l} {psi _ {emn} = cos mvarphi P_ {n} ^ {m} (cos vartheta) z_ {n} ({k} r)} {psi _ {omn} = sin mvarphi P_ {n} ^ {m} (cos vartheta) z_ {n} ({k} r)} конец {массив}}} Вот п п м ( потому что θ ) {displaystyle P_ {n} ^ {m} (cos heta)} ассоциированные полиномы Лежандра , и z п ( k р ) {displaystyle z_ {n} ({k} r)} сферические функции Бесселя .
Векторные сферические гармоники определяются как:
L о е м п = ∇ ψ о е м п {displaystyle mathbf {L} _ {^ {e} _ {o} mn} = mathbf {abla} psi _ {^ {e} _ {o} mn}} M о е м п = ∇ × ( р ψ о е м п ) {displaystyle mathbf {M} _ {^ {e} _ {o} mn} = abla imes left (mathbf {r} psi _ {^ {e} _ {o} mn} ight)} N о е м п = ∇ × M о е м п k {displaystyle mathbf {N} _ {^ {e} _ {o} mn} = {frac {abla imes mathbf {M} _ {^ {e} _ {o} mn}} {k}}} Здесь мы используем действительную угловую часть гармоник, где м ≥ 0 {displaystyle mgeq 0}
Введем обозначения ρ = k р {displaystyle ho = kr}
M е м п ( k , р ) = − м грех ( θ ) грех ( м φ ) п п м ( потому что ( θ ) ) z п ( ρ ) е θ − − потому что ( м φ ) d п п м ( потому что ( θ ) ) d θ z п ( ρ ) е φ {displaystyle {egin {выровнено} {mathbf {M} _ {emn} (k, mathbf {r}) = {{frac {-m} {sin (heta)}} sin (mvarphi) P_ {n} ^ {m } (cos (heta))} z_ {n} (ho) mathbf {e} _ {heta} -} {- cos (mvarphi) {frac {dP_ {n} ^ {m} (cos (heta))} {d heta}}} z_ {n} (ho) mathbf {e} _ {varphi} конец {выровнено}}} M о м п ( k , р ) = м грех ( θ ) потому что ( м φ ) п п м ( потому что ( θ ) ) z п ( ρ ) е θ − − грех ( м φ ) d п п м ( потому что ( θ ) ) d θ z п ( ρ ) е φ {displaystyle {egin {align} {mathbf {M} _ {omn} (k, mathbf {r}) = {{frac {m} {sin (heta)}} cos (mvarphi) P_ {n} ^ {m} (cos (heta))}} z_ {n} (ho) mathbf {e} _ {heta} - {- sin (mvarphi) {frac {dP_ {n} ^ {m} (cos (heta))} { d heta}} z_ {n} (ho) mathbf {e} _ {varphi}} конец {выровнено}}} N е м п ( k , р ) = z п ( ρ ) ρ потому что ( м φ ) п ( п + 1 ) п п м ( потому что ( θ ) ) е р + + потому что ( м φ ) d п п м ( потому что ( θ ) ) d θ 1 ρ d d ρ [ ρ z п ( ρ ) ] е θ − − м грех ( м φ ) п п м ( потому что ( θ ) ) грех ( θ ) 1 ρ d d ρ [ ρ z п ( ρ ) ] е φ {displaystyle {egin {выровнено} {mathbf {N} _ {emn} (k, mathbf {r}) = {frac {z_ {n} (ho)} {ho}} cos (mvarphi) n (n + 1) P_ {n} ^ {m} (cos (heta)) mathbf {e} _ {mathbf {r}} +} {+ cos (mvarphi) {frac {dP_ {n} ^ {m} (cos (heta) )} {d heta}}} {frac {1} {ho}} {frac {d} {dho}} left [ho z_ {n} (ho) ight] mathbf {e} _ {heta} - {- msin (mvarphi) {frac {P_ {n} ^ {m} (cos (heta))} {sin (heta)}}} {frac {1} {ho}} {frac {d} {dho}} left [ ho z_ {n} (ho) ight] mathbf {e} _ {varphi} конец {выровнено}}} N о м п ( k , р ) = z п ( ρ ) ρ грех ( м φ ) п ( п + 1 ) п п м ( потому что ( θ ) ) е р + + грех ( м φ ) d п п м ( потому что ( θ ) ) d θ 1 ρ d d ρ [ ρ z п ( ρ ) ] е θ + + м потому что ( м φ ) п п м ( потому что ( θ ) ) грех ( θ ) 1 ρ d d ρ [ ρ z п ( ρ ) ] е φ {displaystyle {egin {выравнивается} mathbf {N} _ {omn} & (k, mathbf {r}) = {frac {z_ {n} (ho)} {ho}} sin (mvarphi) n (n + 1) P_ {n} ^ {m} (cos (heta)) mathbf {e} _ {mathbf {r}} + & + sin (mvarphi) {frac {dP_ {n} ^ {m} (cos (heta)) } {d heta}} {frac {1} {ho}} {frac {d} {dho}} left [ho z_ {n} (ho) ight] mathbf {e} _ {heta} + & + {mcos (mvarphi) {frac {P_ {n} ^ {m} (cos (heta))} {sin (heta)}}} {frac {1} {ho}} {frac {d} {dho}} left [ho z_ {n} (ho) ight] mathbf {e} _ {varphi} конец {выровнено}}} Радиальная часть магнитных гармоник отсутствует. Для электрических гармоник радиальная часть убывает быстрее, чем угловая, а для больших ρ {displaystyle ho} ρ {displaystyle ho}
Длинные гармоники:
L о е м п ( k , р ) = ∂ ∂ р z п ( k р ) п п м ( потому что θ ) грех потому что м φ е р + 1 р z п ( k р ) ∂ ∂ θ п п м ( потому что θ ) грех потому что м φ е θ ∓ ∓ м р грех θ z п ( k р ) п п м ( потому что θ ) потому что грех м φ е φ {displaystyle {egin {align} mathbf {L} _ {^ {e} _ {o} {mn}} & (k, mathbf {r}) = {frac {partial} {partial r}} z_ {n} ( kr) P_ {n} ^ {m} (cos heta) {^ {cos} _ {sin}} {mvarphi} mathbf {e} _ {r} + & {frac {1} {r}} z_ {n } (kr) {frac {partial} {partial heta}} P_ {n} ^ {m} (cos heta) {^ {cos} _ {sin}} mvarphi mathbf {e} _ {heta} mp & mp {frac {m} {rsin heta}} z_ {n} (kr) P_ {n} ^ {m} (cos heta) {^ {sin} _ {cos}} mvarphi mathbf {e} _ {varphi} end {выровнено} }} Ортогональность Решения векторного уравнения Гельмгольца подчиняются следующим соотношениям ортогональности [7]
∫ 0 2 π ∫ 0 π L о е м п ⋅ L о е м п грех ϑ d ϑ d φ = ( 1 + δ м , 0 ) 2 π ( 2 п + 1 ) 2 ( п + м ) ! ( п − м ) ! k 2 { п [ z п − 1 ( k р ) ] 2 + ( п + 1 ) [ z п + 1 ( k р ) ] 2 } {displaystyle {int _ {0} ^ {2pi} int _ {0} ^ {pi} mathbf {L} _ {^ {e} _ {o} mn} cdot mathbf {L} _ {^ {e} _ { o} mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {(2n + 1) ^ {2}}} {frac {(n + m)!} { (nm)!}} k ^ {2} left {nleft [z_ {n-1} (kr) ight] ^ {2} + (n + 1) left [z_ {n + 1} (kr) ight] ^ {2} ight}}} ∫ 0 2 π ∫ 0 π M о е м п ⋅ M о е м п грех ϑ d ϑ d φ = ( 1 + δ м , 0 ) 2 π 2 п + 1 ( п + м ) ! ( п − м ) ! п ( п + 1 ) [ z п ( k р ) ] 2 {displaystyle {int _ {0} ^ {2pi} int _ {0} ^ {pi} mathbf {M} _ {^ {e} _ {o} mn} cdot mathbf {M} _ {^ {e} _ { o} mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {2n + 1}} {frac {(n + m)!} {(нм)!}} n (n + 1) осталось [z_ {n} (kr) ight] ^ {2}}} ∫ 0 2 π ∫ 0 π N о е м п ⋅ N о е м п грех ϑ d ϑ d φ = ( 1 + δ м , 0 ) 2 π ( 2 п + 1 ) 2 ( п + м ) ! ( п − м ) ! п ( п + 1 ) { ( п + 1 ) [ z п − 1 ( k р ) ] 2 + п [ z п + 1 ( k р ) ] 2 } {displaystyle int _ {0} ^ {2pi} int _ {0} ^ {pi} mathbf {N} _ {^ {e} _ {o} mn} cdot mathbf {N} _ {^ {e} _ {o } mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {(2n + 1) ^ {2}}} {frac {(n + m)!} {( nm)!}} n (n + 1) влево {(n + 1) влево [z_ {n-1} (kr) ight] ^ {2} + nleft [z_ {n + 1} (kr) ight] ^ {2} ight}} ∫ 0 π ∫ 0 2 π L о е м п ⋅ N о е м п грех ϑ d ϑ d φ = ( 1 + δ м , 0 ) 2 π ( 2 п + 1 ) 2 ( п + м ) ! ( п − м ) ! п ( п + 1 ) k { [ z п − 1 ( k р ) ] 2 − [ z п + 1 ( k р ) ] 2 } {displaystyle {int _ {0} ^ {pi} int _ {0} ^ {2pi} mathbf {L} _ {^ {e} _ {o} mn} cdot mathbf {N} _ {^ {e} _ { o} mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {(2n + 1) ^ {2}}} {frac {(n + m)!} { (нм)!}} n (n + 1) левый {левый [z_ {n-1} (kr) полет] ^ {2} -левый [z_ {n + 1} (kr) полет] ^ {2} полет }}} Все остальные интегралы по углам между разными функциями или функциями с разными индексами равны нулю.
Динамика жидкостей При расчете Закон Стокса для сопротивления, которое вязкая жидкость оказывает на небольшую сферическую частицу, распределение скоростей подчиняется Уравнения Навье-Стокса пренебрегая инерцией, т.е.
∇ ⋅ v = 0 , 0 = − ∇ п + η ∇ 2 v , {displaystyle {egin {выровнено} abla cdot mathbf {v} & = 0, mathbf {0} & = - abla p + eta abla ^ {2} mathbf {v}, конец {выровнено}}} с граничными условиями
v = 0 ( р = а ) , v = − U 0 ( р → ∞ ) . {displaystyle {egin {align} mathbf {v} & = mathbf {0} quad (r = a), mathbf {v} & = - mathbf {U} _ {0} quad (r o infty) .end {выровнено) }}} куда U - относительная скорость частицы относительно жидкости вдали от частицы. В сферических координатах эту скорость на бесконечности можно записать как
U 0 = U 0 ( потому что θ р ^ − грех θ θ ^ ) = U 0 ( Y 10 + Ψ 10 ) . {displaystyle mathbf {U} _ {0} = U_ {0} left (cos heta, {hat {mathbf {r}}} - sin heta, {hat {mathbf {heta}}} ight) = U_ {0} left (mathbf {Y} _ {10} + mathbf {Psi} _ {10} ight).} Последнее выражение предполагает разложение по сферическим гармоникам для скорости жидкости и давления
п = п ( р ) Y 10 , v = v р ( р ) Y 10 + v ( 1 ) ( р ) Ψ 10 . {displaystyle {egin {выровнено} p & = p (r) Y_ {10}, mathbf {v} & = v ^ {r} (r) mathbf {Y} _ {10} + v ^ {(1)} ( r) mathbf {Psi} _ {10} .end {выровнено}}} Подстановка в уравнения Навье – Стокса дает набор обыкновенных дифференциальных уравнений для коэффициентов.
Интегральные отношения Здесь используются следующие определения:
Y е м п = потому что м φ п п м ( потому что θ ) Y о м п = грех м φ п п м ( потому что θ ) {displaystyle {egin {align} Y_ {emn} & = cos mvarphi P_ {n} ^ {m} (cos heta) Y_ {omn} & = sin mvarphi P_ {n} ^ {m} (cos heta) end { выровнено}}} Икс о е м п ( k k ) = ∇ × ( k Y е о м п ( k k ) ) {displaystyle mathbf {X} _ {^ {e} _ {o} mn} left ({frac {mathbf {k}} {k}} ight) = abla imes left (mathbf {k} Y _ {^ {o} _ {e} mn} left ({frac {mathbf {k}} {k}} ight) ight)} Z е о м п ( k k ) = я k k × Икс о е м п ( k k ) {displaystyle mathbf {Z} _ {^ {o} _ {e} mn} left ({frac {mathbf {k}} {k}} ight) = i {frac {mathbf {k}} {k}} imes mathbf {X} _ {^ {e} _ {o} mn} влево ({frac {mathbf {k}} {k}} ight)} В случае, если вместо z п {displaystyle z_ {n}} сферические функции Бесселя , с помощью расширение плоской волны можно получить следующие интегральные соотношения: [8]
N п м п ( k , р ) = я − п 4 π ∫ Z п м п ( k k ) е я k р d Ω k {displaystyle mathbf {N} _ {pmn} (k, mathbf {r}) = {frac {i ^ {- n}} {4pi}} int mathbf {Z} _ {pmn} left ({frac {mathbf {k }} {k}} ight) e ^ {imathbf {k} mathbf {r}} dOmega _ {k}} M п м п ( k , р ) = я − п 4 π ∫ Икс п м п ( k k ) е я k р d Ω k {displaystyle mathbf {M} _ {pmn} (k, mathbf {r}) = {frac {i ^ {- n}} {4pi}} int mathbf {X} _ {pmn} left ({frac {mathbf {k }} {k}} ight) e ^ {imathbf {k} mathbf {r}} dOmega _ {k}} В случае, когда z п {displaystyle z_ {n}} [9] [8]
M п м п ( 3 ) ( k , р ) = я − п 2 π k ∬ − ∞ ∞ d k ‖ е я ( k Икс Икс + k у у ± k z z ) k z [ Икс п м п ( k k ) ] {displaystyle mathbf {M} _ {pmn} ^ {(3)} (k, mathbf {r}) = {frac {i ^ {- n}} {2pi k}} iint _ {- infty} ^ {infty} dk_ {|} {frac {e ^ {ileft (k_ {x} x + k_ {y} ypm k_ {z} zight)}} {k_ {z}}} left [mathbf {X} _ {pmn} left ( {frac {mathbf {k}} {k}} ight) ight]} N п м п ( 3 ) ( k , р ) = я − п 2 π k ∬ − ∞ ∞ d k ‖ е я ( k Икс Икс + k у у ± k z z ) k z [ Z п м п ( k k ) ] {displaystyle mathbf {N} _ {pmn} ^ {(3)} (k, mathbf {r}) = {frac {i ^ {- n}} {2pi k}} iint _ {- infty} ^ {infty} dk_ {|} {frac {e ^ {ileft (k_ {x} x + k_ {y} ypm k_ {z} zight)}} {k_ {z}}} left [mathbf {Z} _ {pmn} left ( {frac {mathbf {k}} {k}} ight) ight]} куда k z = k 2 − k Икс 2 − k у 2 {displaystyle k_ {z} = {sqrt {k ^ {2} -k_ {x} ^ {2} -k_ {y} ^ {2}}}} ( 3 ) {displaystyle (3)}
Смотрите также Рекомендации ^ Barrera, RG; Эстевес, Г. А.; Хиральдо, Дж. (1 октября 1985 г.). «Векторные сферические гармоники и их приложение в магнитостатике». Европейский журнал физики . IOP Publishing. 6 (4): 287–294. Bibcode :1985EJPh .... 6..287B . Дои :10.1088/0143-0807/6/4/014 . ISSN 0143-0807 . ^ Карраскал, B; Эстевес, Г. А.; Ли, Пейлиан; Лоренцо, V (1991-07-01). «Векторные сферические гармоники и их приложение к классической электродинамике». Европейский журнал физики . IOP Publishing. 12 (4): 184–191. Bibcode :1991EJPh ... 12..184C . Дои :10.1088/0143-0807/12/4/007 . ISSN 0143-0807 . ^ Хилл, Э. Л. (1954). «Теория векторных сферических гармоник» (PDF) . Американский журнал физики . Американская ассоциация учителей физики (AAPT). 22 (4): 211–214. Bibcode :1954AmJPh..22..211H . Дои :10.1119/1.1933682 . ISSN 0002-9505 . S2CID 124182424 . ^ Вайнберг, Эрик Дж. (1994-01-15). «Монопольные векторные сферические гармоники». Физический обзор D . Американское физическое общество (APS). 49 (2): 1086–1092. arXiv :hep-th / 9308054 Bibcode :1994ПхРвД..49.1086Вт . Дои :10.1103 / Physrevd.49.1086 . ISSN 0556-2821 . PMID 10017069 . S2CID 6429605 . ^ ВЕЧЕРА. Морзе и Х. Фешбах, Методы теоретической физики, часть II , Нью-Йорк: Макгроу-Хилл, 1898-1901 (1953) ^ Борен, Крейг Ф. и Дональд Р. Хаффман, Поглощение и рассеяние света малыми частицами, Нью-Йорк: Wiley, 1998, 530 стр., ISBN 0-471-29340-7, ISBN 978-0-471-29340-8 (второе издание) ^ а б Страттон, Дж. А. (1941). Электромагнитная теория ^ а б Б. Стаут,Суммы решеток сферических гармоник для решеток. В кн .: Попов Э., редактор. Решетки: теория и численные приложения. Институт Френеля, Университет Экс-Марсель 6 (2012). ^ Р. К. Виттманн, Операторы сферических волн и формулы трансляции, IEEE Transactions on Antennas and Propagation 36, 1078-1087 (1988) внешняя ссылка 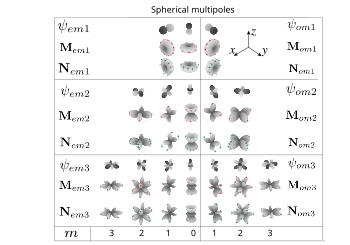
























































![{displaystyle {egin {выровнено} {mathbf {N} _ {emn} (k, mathbf {r}) = {frac {z_ {n} (ho)} {ho}} cos (mvarphi) n (n + 1) P_ {n} ^ {m} (cos (heta)) mathbf {e} _ {mathbf {r}} +} {+ cos (mvarphi) {frac {dP_ {n} ^ {m} (cos (heta) )} {d heta}}} {frac {1} {ho}} {frac {d} {dho}} left [ho z_ {n} (ho) ight] mathbf {e} _ {heta} - {- msin (mvarphi) {frac {P_ {n} ^ {m} (cos (heta))} {sin (heta)}}} {frac {1} {ho}} {frac {d} {dho}} left [ ho z_ {n} (ho) ight] mathbf {e} _ {varphi} конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ad38d781b484c1a1b550920518d596c88de2c37)
![{displaystyle {egin {выравнивается} mathbf {N} _ {omn} & (k, mathbf {r}) = {frac {z_ {n} (ho)} {ho}} sin (mvarphi) n (n + 1) P_ {n} ^ {m} (cos (heta)) mathbf {e} _ {mathbf {r}} + & + sin (mvarphi) {frac {dP_ {n} ^ {m} (cos (heta)) } {d heta}} {frac {1} {ho}} {frac {d} {dho}} left [ho z_ {n} (ho) ight] mathbf {e} _ {heta} + & + {mcos (mvarphi) {frac {P_ {n} ^ {m} (cos (heta))} {sin (heta)}}} {frac {1} {ho}} {frac {d} {dho}} left [ho z_ {n} (ho) ight] mathbf {e} _ {varphi} конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4528c43603f7c5868f920afcbdae5bec0d6f1af3)


![{displaystyle {int _ {0} ^ {2pi} int _ {0} ^ {pi} mathbf {L} _ {^ {e} _ {o} mn} cdot mathbf {L} _ {^ {e} _ { o} mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {(2n + 1) ^ {2}}} {frac {(n + m)!} { (nm)!}} k ^ {2} left {nleft [z_ {n-1} (kr) ight] ^ {2} + (n + 1) left [z_ {n + 1} (kr) ight] ^ {2} ight}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3caf9a3a862e813514a86ae833494cfd4f0f9c8a)
![{displaystyle {int _ {0} ^ {2pi} int _ {0} ^ {pi} mathbf {M} _ {^ {e} _ {o} mn} cdot mathbf {M} _ {^ {e} _ { o} mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {2n + 1}} {frac {(n + m)!} {(нм)!}} n (n + 1) осталось [z_ {n} (kr) ight] ^ {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61acd92c5fd19ad05b94d6e9792241b6dc468972)
![{displaystyle int _ {0} ^ {2pi} int _ {0} ^ {pi} mathbf {N} _ {^ {e} _ {o} mn} cdot mathbf {N} _ {^ {e} _ {o } mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {(2n + 1) ^ {2}}} {frac {(n + m)!} {( nm)!}} n (n + 1) влево {(n + 1) влево [z_ {n-1} (kr) ight] ^ {2} + nleft [z_ {n + 1} (kr) ight] ^ {2} ight}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6304776dd0142be5974ab4f30dd4b895cc093fb0)
![{displaystyle {int _ {0} ^ {pi} int _ {0} ^ {2pi} mathbf {L} _ {^ {e} _ {o} mn} cdot mathbf {N} _ {^ {e} _ { o} mn} sin vartheta dvartheta dvarphi} {= (1 + delta _ {m, 0}) {frac {2pi} {(2n + 1) ^ {2}}} {frac {(n + m)!} { (нм)!}} n (n + 1) левый {левый [z_ {n-1} (kr) полет] ^ {2} -левый [z_ {n + 1} (kr) полет] ^ {2} полет }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/550cfe2b979c59738bfb9c3213cc844a29dad4dd)










![{displaystyle mathbf {M} _ {pmn} ^ {(3)} (k, mathbf {r}) = {frac {i ^ {- n}} {2pi k}} iint _ {- infty} ^ {infty} dk_ {|} {frac {e ^ {ileft (k_ {x} x + k_ {y} ypm k_ {z} zight)}} {k_ {z}}} left [mathbf {X} _ {pmn} left ( {frac {mathbf {k}} {k}} ight) ight]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/916898171326fa77d2c6b525ee23a44893581bdb)
![{displaystyle mathbf {N} _ {pmn} ^ {(3)} (k, mathbf {r}) = {frac {i ^ {- n}} {2pi k}} iint _ {- infty} ^ {infty} dk_ {|} {frac {e ^ {ileft (k_ {x} x + k_ {y} ypm k_ {z} zight)}} {k_ {z}}} left [mathbf {Z} _ {pmn} left ( {frac {mathbf {k}} {k}} ight) ight]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a6b0db1d3b540dc4324d7fbefc7be994862b50f)

