Правила Вудворда – Хоффмана - Woodward–Hoffmann rules

В Правила Вудворда – Хоффмана (или перициклические правила отбора),[1] разработан Роберт Бернс Вудворд и Роальд Хоффманн, представляют собой набор правил, используемых для рационализации или прогнозирования определенных аспектов стереохимия и энергия активации из перициклические реакции, важный класс реакций в органическая химия. Правила лучше всего понять с точки зрения концепции сохранение орбитальной симметрии с помощью диаграммы орбитальной корреляции, для которых элементарное описание дано в Разделе 10.4 учебника для учащихся.[2] Правила Вудворда-Хоффмана являются следствием изменений в электронной структуре, которые происходят во время перициклической реакции, и основываются на фазировании взаимодействующих молекулярные орбитали. Они применимы ко всем классам перициклических реакций (и их микроскопическим обратным `` ретро '' процессам), включая (1) электроциклизация, (2) циклоприсоединения, (3) сигматропные реакции, (4) реакции группового переноса, (5) ее реакции,[3] (6) хелетропные реакции,[4] и (7) диотропные реакции.[5] Благодаря своей элегантности, простоте и общности правила Вудворда-Хоффмана считаются первыми примером силы теория молекулярных орбиталей химикам-экспериментаторам.[6]
Вудвард и Хоффманн разработали правила перициклического отбора, исследуя корреляции между орбиталями реагента и продукта (то есть, как орбитали реагента и продукта связаны друг с другом непрерывными геометрическими искажениями, которые являются функциями координаты реакции). Они определили сохранение орбитальной симметрии как важнейший теоретический принцип, определяющий результат (или осуществимость) перициклического процесса. Были предложены и другие теоретические подходы, ведущие к тем же правилам отбора. Хоффманн был удостоен награды 1981 г. Нобелевская премия по химии за выяснение важности орбитальной симметрии в перициклических реакциях, которую он разделял с Кеничи Фукуи. Фукуи разработал аналогичный набор идей в рамках пограничная молекулярная орбиталь (FMO) теория. Поскольку Вудворд умер двумя годами ранее, он не имел права получить вторую Нобелевскую премию по химии.[7]
Предпосылки и терминология
А перициклическая реакция представляет собой органическую реакцию, которая протекает через единый согласованный и циклический переходное состояние, геометрия которого допускает непрерывное перекрытие цикла (π и / или σ) орбитали. На языке орбитальной симметрии перициклическая реакция называется запрещенный симметрией если существует дополнительный энергетический барьер, обусловленный симметрией, возникающий из-за предполагаемой корреляции электронной конфигурации основного состояния исходного материала с электронной конфигурацией возбужденного состояния продукта и наоборот. (Хотя правило непересечения запрещает такую корреляцию, рост энергии по мере приближения намеченного пересечения, тем не менее, приводит к дополнительному энергетическому барьеру.) Перициклическая реакция классифицируется как разрешенная симметрия если такого барьера симметрии не существует. Таким образом, эти условия не подразумевают, действительно ли будет иметь место рассматриваемая реакция. Напротив, при прочих равных энергетических факторах запрещенному по симметрии процессу будет препятствовать дополнительный энергетический барьер. Хотя барьер, налагаемый симметрией, часто бывает огромным (примерно до 5 эВ или 480 кДж / моль в случае запрещенного [2 + 2] циклоприсоединения), запрет не является абсолютным, и реакции, запрещенные по симметрии, все же могут иметь место. через перициклический путь, если другие факторы (например, высвобождение штамма) способствуют реакции. Точно так же разрешенная симметрия реакция может быть предотвращена непреодолимым энергетическим барьером, возникающим из-за факторов, не связанных с орбитальной симметрией.
Правила Вудворда – Хоффмана были впервые сформулированы в 1965 году для объяснения поразительного стереоспецифичность из электроциклический реакции под тепловой и фотохимический контроль. Стереохимия электроциклизации была синтетически важна в контексте давних усилий Вудворда синтезировать витамин B12, а наблюдения, сделанные в ходе синтеза, послужили вдохновением для формулировки правил Вудворда – Хоффмана. Взаимопревращение модельных производных циклобутена и бутадиена под действием термических (нагрев) и фотохимических (Ультрафиолетовый облучения) является иллюстративным.[8] Термолиз из транс-1,2,3,4-тетраметил-1-циклобутен (1) дает только один геометрический изомер, (E,E) -3,4-диметил-2,4-гексадиен (2); (Z,Z) и (E,Z) геометрические изомеры в смеси продуктов не обнаружены. Аналогичным образом термолиз СНГ-1,2,3,4-тетраметил-1-циклобутен (3) предоставляется только (E,Z) изомер 4.[9] В обеих реакциях раскрытия кольца атомы углерода на концах разрывающейся σ-связи вращаются в одно и тоже направление.[10] С другой стороны, при фотохимической активации наблюдается противоположный стереохимический курс: когда родственное соединение (E,E) -2,4-гексадиен (5) подвергся воздействию света, СНГ-3,4-диметил-1-циклобутен (6) образовалась исключительно в результате замыкания электроциклического кольца.[11] Это требует, чтобы концы π-системы вращались в противоположный направления для образования новой σ-связи. Термолиз 6 следует тому же стереохимическому курсу, что и 3: раскрытие электроциклического кольца приводит к образованию (E,Z) -2,4-гексадиен (7) и нет 5.[12]

Условия соперничающий и отвратительный были придуманы для описания относительного направления вращения связей, участвующих в электроциклических реакциях раскрытия и замыкания кольца. Когда два конца разрывного или образующего соединения вращаются в одно и тоже направление (как по часовой стрелке, так и против часовой стрелки - как в случае открытия кольца 1, 3 или же 6 в тепловых условиях), процесс называется соперничающий. Когда два конца вращаются противостоящий направления (один по часовой стрелке, один против часовой стрелки - как при фотохимическом замыкании кольца 5), процесс называется отвратительный. Было обнаружено, что 4н-электронно-тепловые и (4п + 2) -электронные фотохимические электроциклические реакции в целом были взаимно вращательными, а 4н-электронно-фотохимические и (4п + 2) -электронные термические электроциклические реакции в целом были дихотирующими. Впервые эта закономерность была объяснена в 1965 году, когда Вудворд и Хоффманн предложили сохранение орбитальной симметрии (см. Ниже) в качестве ключевого принципа, который определяет стереохимический ход электроциклических реакций.
В конце концов, было признано, что перициклические реакции с термическим стимулированием в целом подчиняются единому набору общих правил отбора, зависящих от количества электронов и топологии орбитальных взаимодействий. Ключевая концепция орбитальная топология или же лицо был введен для объединения нескольких классов перициклических реакций в рамках единой концептуальной основы. Короче говоря, набор смежных атомов и связанных с ними орбиталей, которые реагируют как единое целое в перициклической реакции, известен как компонент, и каждый компонент называется антарафациальный или же надфасциальный в зависимости от того, находятся ли взаимодействующие во время реакции орбитальные доли на противоположной или той же стороне от узловой плоскости соответственно. (Старые термины конротаторный и дисротативный, которые применимы только к электроциклическому открытию и замыканию кольца, включены в эту более общую систему классификации терминами антарафациальный и надфасциальный соответственно.) Учитывая эти общие определения, правила Вудворда-Хоффмана могут быть изложено лаконично одним предложением:[13]
Обобщенное перициклическое правило отбора. Перициклический процесс в основном состоянии с участием N электронных пар и A антарафациальных компонентов является симметричным тогда и только тогда, когда N + A нечетно.
Перициклический процесс в основном состоянии вызывается добавлением тепловой энергии (т. Е. Нагреванием системы, символизируемым Δ ). Напротив, перициклический процесс в возбужденном состоянии имеет место, если реагент переводится в электронно-возбужденное состояние путем активации с помощью ультрафиолетовый свет (т.е. облучение системы, символизируемое часν ). Однако важно признать, что действующий механизм формально перициклической реакции, имеющей место при фотохимическом облучении, обычно не так прост и ясен, как предполагает эта дихотомия. Обычно возможны несколько режимов электронного возбуждения, и электронно-возбужденные молекулы могут испытывать межсистемный переход, безызлучательный распад или релаксация к неблагоприятной равновесной геометрии до того, как может иметь место перициклический процесс в возбужденном состоянии. Таким образом, многие очевидные перициклические реакции, протекающие при облучении, на самом деле считаются ступенчатыми процессами с участием бирадикальных интермедиатов. Тем не менее, часто наблюдается обратное изменение правил перициклического отбора при переключении с термической активации на фотохимическую. Это можно объяснить, если рассмотреть корреляцию первых электронных возбужденных состояний реагентов и продуктов. Хотя это скорее полезная эвристика, чем правило, можно сформулировать соответствующий обобщенный принцип выбора для фотохимических перициклических реакций: Перициклический процесс с участием N электронных пар и антарафациальных компонентов A часто предпочтителен в фотохимических условиях, если N + A четное. Также известны перициклические реакции с участием нечетного числа электронов. Что касается применения обобщенного правила перициклического отбора, эти системы обычно можно рассматривать так, как если бы участвовал еще один электрон.[14]
Между первоначальным развитием принципа сохранения орбитальной симметрии в 1965 году Вудвордом и Хоффманном и их заявлением об обобщенном перициклическом правиле отбора в 1969 году, Говард Циммерман[15][16] и Майкл Дж. С. Дьюар[17][18] предложил не менее общую концептуальную основу, известную как Концепция Мебиуса-Хюккеля, или же теория ароматических переходных состояний для объяснения реакционной способности и селективности перициклических систем, в то время как Кеничи Фукуи[19][20] проанализировали перициклические системы, используя принципы пограничная орбитальная теория. В подходе Дьюара-Циммермана топология орбитального перекрытия (Хюккеля или Мёбиуса) и полное количество электронов в системе (4п + 2 или 4п) приводят к переходным состояниям, которые классифицируются как ароматические или антиароматические. На языке теории ароматических переходных состояний правила Вудворда – Хоффмана можно переформулировать следующим образом: перициклическое переходное состояние, включающее (4п + 2) электронов с топологией Хюккеля или 4п электронов с топологией Мёбиуса является ароматическим и разрешенным, в то время как перициклическое переходное состояние с участием 4п-электроны с топологией Хюккеля или (4п + 2) -электроны с топологией Мёбиуса антиароматичны и запрещены. Подход Фукуи, с другой стороны, анализирует взаимодействия между HOMO и LUMO каждого из реагентов или внутри реагента. Процесс, в котором взаимодействие HOMO-LUMO является конструктивным (приводит к чистому связывающему взаимодействию), является благоприятным и считается допустимым по симметрии, в то время как процесс, в котором взаимодействие HOMO-LUMO является неконструктивным (приводит к связывающим и разрыхляющим взаимодействиям, которые отменяют ) является неблагоприятным и считается запрещенным по симметрии. Подход с использованием корреляционной диаграммы (сохранение орбитальной симметрии, см. выше), как было предложено Вудвордом и Хоффманном и разъяснено Лонге-Хиггинс и другие, привели к общему утверждению, что перициклическая реакция допустима, если сумма числа надфасциальных 4q + 2 компонента и кол-во антарафациальных 4р компоненты нечетные. Важно отметить, что хотя концептуально разные, теория ароматических переходных состояний (Циммерман и Дьюар), пограничная теория молекулярных орбиталей (Фукуи) и принцип сохранения орбитальной симметрии (Вудворд и Хоффман) дают идентичные предсказания.
Хотя орбитальная «симметрия» используется в качестве инструмента для построения диаграмм орбиты и корреляции состояний, абсолютное присутствие или отсутствие элемента симметрии не критично для определения того, разрешена или запрещена реакция. То есть введение простого заместителя, который формально нарушает плоскость или ось симметрии (например, метильная группа), обычно не влияет на оценку того, разрешена или запрещена реакция. Вместо этого симметрия, присутствующая в незамещенном аналоге, используется, чтобы упростить построение диаграмм орбитальной корреляции и избежать необходимости выполнять вычисления.[21] Только фазовые соотношения между орбиталями важны при оценке того, разрешена или запрещена реакция "симметрии". Более того, орбитальные корреляции все еще могут быть сделаны, даже если нет сохраняющихся элементов симметрии (например, 1,5-сигматропные сдвиги и еновые реакции). По этой причине анализы Вудворда – Хоффмана, Фукуи и Дьюара – Циммермана одинаково широко применимы, хотя один подход может быть проще или более интуитивно понятным для применения, чем другой, в зависимости от реакции, которую человек желает проанализировать.
Оригинальная рецептура
Правила Вудворда – Хоффмана были впервые применены для объяснения наблюдаемого стереоспецифичность из электроциклический открытие кольца и реакции замыкания кольца на концах разомкнутой цепи сопряженный полиены либо путем применения тепла (тепловые реакции), либо путем воздействия света (фотохимический реакции).
В оригинальной публикации 1965 г.[22] три правила, извлеченные из экспериментальных данных и молекулярно-орбитального анализа, выглядят следующим образом:
- В системе с открытой цепью, содержащей 4п π электроны, то орбитальная симметрия из самая высокая занятая орбиталь молекулы таков, что скрепляющее взаимодействие между концами должно включать перекрытие между орбитальными оболочками на противоположных сторонах системы, и это может быть достигнуто только в соперничающий процесс.
- В открытых системах, содержащих (4п + 2) π электронов, терминальное связывающее взаимодействие внутри молекул в основном состоянии требует перекрытия орбитальных огибающих на одной и той же поверхности системы, достижимого только за счет дисротационных смещений.
- В фотохимическая реакция электрон в HOMO реагента превращается в возбужденное состояние что приводит к изменению терминальных отношений симметрии и стереоспецифичности.
Используя эту формулировку, можно понять стереоспецифичность электроциклического замыкания кольца замещенного бута-1,3-диена, изображенного ниже. Бута-1,3-диен имеет 4 -электронов в основном состоянии и, таким образом, проходит через механизм одновременного замыкания кольца. (Правила Вудворда – Хоффмана ничего не говорят о положении равновесия для перициклических процессов. Для циклобутена бутадиен, равновесие лежит далеко вправо (кольцо разомкнуто), а для циклогексадиена гексатриен, равновесие лежит далеко влево (кольцо замкнуто). Без потери общности здесь все анализы выполняются в направлении замыкания кольца.)
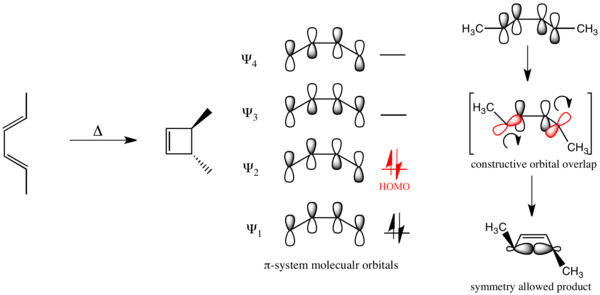
Напротив, при электроциклическом замыкании кольца замещенного гекса-1,3,5-триена, изображенного ниже, реакция протекает по дисротационному механизму.

В случае электроциклического замыкания бута-1,3-диена с фотохимическим воздействием электронное продвижение вызывает чтобы стать HOMO, и механизм реакции должен быть дисротаторным.
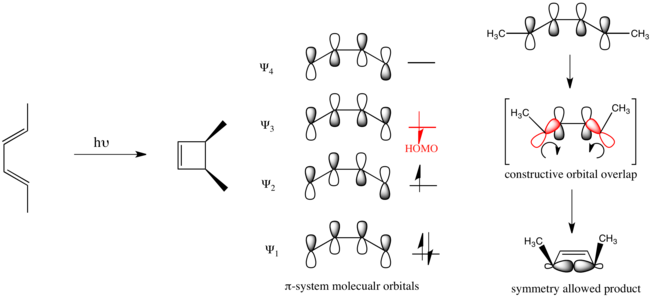
Считается, что органические реакции, подчиняющиеся этим правилам, допускают симметрию. Реакции, протекающие в обратном направлении, запрещены по симметрии и требуют значительно большего количества энергии, если они вообще имеют место.
Диаграммы корреляции
Как показано Лонге-Хиггинс и Э. В. Абрахамсон, правила Вудворда – Хоффмана также могут быть выведены путем изучения диаграмма корреляции данной реакции.[23][14][24][25] А элемент симметрии это точка отсчета (обычно плоскость или линия), относительно которой объект симметричен относительно операции симметрии. Если симметрия элемент присутствует на протяжении всего механизма реакции (реагент, переходное состояние и продукт), он называется сохраняющимся элементом симметрии. Тогда на протяжении всей реакции должна сохраняться симметрия молекулярных орбиталей относительно этого элемента. То есть молекулярные орбитали, которые являются симметричными относительно элемента симметрии в исходном материале, должны быть коррелированы (преобразованы в) орбиталями, симметричными относительно этого элемента в продукте. Наоборот, то же самое утверждение верно для антисимметрии относительно сохраняющегося элемента симметрии. Диаграмма корреляции молекулярных орбиталей коррелирует молекулярные орбитали исходных материалов и продукта на основе сохранения симметрии. Из диаграмма корреляции молекулярных орбиталей можно построить диаграмма корреляции электронных состояний который коррелирует электронные состояния (то есть основное состояние и возбужденные состояния) реагентов с электронными состояниями продуктов. Затем корреляционные диаграммы можно использовать для прогнозирования высоты барьеров переходного состояния.[26]
Электроциклические реакции


С учетом электроциклического замыкания кольца замещенного 1,3-бутадиена реакция может протекать либо через соперничающий или отвратительный механизм реакции. Как показано слева, в конротаторном переходном состоянии есть C2 ось симметрии и в дисротативном переходном состоянии имеется σ плоскость зеркала симметрии. Чтобы соотнести орбитали исходного материала и продукта, необходимо определить, являются ли молекулярные орбитали симметричными или антисимметричными относительно этих элементов симметрии. Молекулярные орбитали бутадиена π-системы показаны справа вместе с элементом симметрии, с которым они симметричны. Они антисимметричны по отношению к другому. Например, Ψ2 1,3-бутадиена симметричен относительно 180о вращение вокруг C2 оси и антисимметричны относительно отражения в плоскости зеркала.
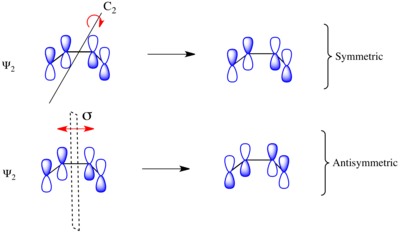
Ψ1 и Ψ3 симметричны относительно плоскости зеркала, так как знак лепестков p-орбиты сохраняется при преобразовании симметрии. Аналогично Ψ1 и Ψ3 антисимметричны относительно C2 оси, поскольку вращение меняет знак p-орбитальных долей равномерно. Наоборот Ψ2 и Ψ4 симметричны относительно C2 ось и антисимметрична относительно плоскости σ-зеркала.

Такой же анализ можно провести для молекулярных орбиталей циклобутена. Результат обеих операций симметрии для каждой МО показан слева. Поскольку σ и σ* орбитали целиком лежат в плоскости, содержащей C2 перпендикулярны σ, они равномерно симметричны и антисимметричны (соответственно) обоим элементам симметрии. С другой стороны, π симметрично относительно отражения и антисимметрично относительно вращения, а π* антисимметричен относительно отражения и симметричен относительно вращения.
Линии корреляции проводятся для соединения молекулярных орбиталей в исходном материале и продукте, которые имеют одинаковую симметрию относительно сохраняющегося элемента симметрии. В случае обратного 4-электронного электроциклического замыкания 1,3-бутадиена нижняя молекулярная орбиталь1 асимметричен (A) относительно C2 ось. Таким образом, эта молекулярная орбиталь коррелирует с π-орбиталью циклобутена, орбитали с наименьшей энергией, которая также является (A) по отношению к C2 ось. Аналогично Ψ2, который является симметричным (S) относительно C2 ось коррелирует с σ циклобутена. Последние две корреляции находятся между антисимметричными (A) молекулярными орбиталями Ψ3 и σ*, а симметричные (S) молекулярные орбитали Ψ4 и π*.[14]

Точно так же существует диаграмма корреляции для дисротационного механизма. В этом механизме элементом симметрии, который сохраняется на протяжении всего механизма, является σ-зеркальная плоскость отражения. Здесь наименьшая энергия MO Ψ1 1,3-бутадиен симметричен относительно плоскости отражения и, как таковой, коррелирует с симметричной σ МО циклобутена. Точно так же пара симметричных молекулярных орбиталей с более высокой энергией Ψ3 и π коррелируют. Что касается асимметричных молекулярных орбиталей, то пара с меньшей энергией Ψ2 и π* образуют корреляционную пару, как и Ψ4 и σ*.[14]

Оценивая два механизма, конротаторный механизм будет иметь более низкий барьер потому что он преобразует электроны из основное состояние орбитали реагентов (Ψ1 и Ψ2) на орбитали основного состояния произведения (σ и π). И наоборот, дисротационный механизм заставляет преобразование Ψ1 орбиталь на орбиталь σ, а Ψ2 орбиталь в π* орбитальный. Таким образом, два электрона в основном состоянии Ψ2 орбитали переходят на возбужденную разрыхляющую орбиталь, создавая двойную возбужденное электронное состояние циклобутена. Это привело бы к значительно более высокому переходному состоянию барьера для реакции.[14]

Однако, поскольку реакции происходят не между несвязанными молекулярными орбиталями, а между электронными состояниями, окончательный анализ включает диаграммы корреляции состояний. Диаграмма корреляции состояний коррелирует общую симметрию электронных состояний в исходном материале и продукте. В основное состояние 1,3-бутадиена, как показано выше, имеет 2 электрона в Ψ1 и 2 электрона в Ψ2, поэтому он представлен как Ψ12Ψ22. Общая симметрия состояния - это произведение симметрий каждой заполненной орбитали с множественностью для дважды населенных орбиталей. Таким образом, поскольку Ψ1 несимметрична относительно C2 ось, а Ψ2 симметрично, полное состояние представлено A2S2. Чтобы понять, почему этот конкретный продукт является математически общим S, это S можно представить как (+1), а A как (−1). Это происходит из того факта, что знаки лепестков p-орбиталей умножаются на (+1), если они симметричны по отношению к преобразованию симметрии (т. Е. Без изменений), и умножаются на (-1), если они антисимметричны относительно преобразование симметрии (т.е. инвертированное). Таким образом, A2S2=(−1)2(+1)2= + 1 = S. Первое возбужденное состояние (ES-1) образуется при продвижении электрона из HOMO к LUMO, и поэтому представляется как is12Ψ2Ψ3. Как Ψ1это A, Ψ2 есть S, и Ψ3 есть A, симметрия этого состояния задается формулой A2SA = A.

Теперь, учитывая электронные состояния продукта, циклобутена, основное состояние определяется выражением σ2π2, имеющий симметрию S2А2= S. Первое возбужденное состояние (ES-1 ') снова образуется в результате продвижения электрона из HOMO к LUMO, поэтому в данном случае он представлен как σ2ππ*. Симметрия этого состояния S2АС = А.
Основное состояние Ψ12Ψ22 1,3-бутадиена коррелирует с основным состоянием σ2π2 циклобутена, как показано на диаграмме корреляции МО выше. Ψ1 коррелирует с π и Ψ2 коррелирует с σ. Таким образом, орбитали, составляющие Ψ12Ψ22 должны переходить в орбитали, составляющие σ2π2 под вращательный механизм. Однако состояние ES-1 не коррелирует с состоянием ES-1 ', поскольку молекулярные орбитали не трансформируются друг в друга в соответствии с требованием симметрии, наблюдаемым на диаграмме корреляции молекулярных орбиталей. Вместо1 коррелирует с π, Ψ2 коррелирует с σ, а Ψ3 коррелирует с σ*, состояние Ψ12Ψ2Ψ3 пытается превратиться в π2σσ*, которое представляет собой другое возбужденное состояние. Итак, ES-1 пытается коррелировать с ES-2 '= σπ2σ*, который по энергии выше, чем Es-1 '. Аналогично ES-1 '= σ2ππ* пытается соотнести с ES-2 = Ψ1Ψ22Ψ4. Эти корреляции не могут иметь место из-за квантово-механического правила, известного как правило избегания пересечения. Это говорит о том, что энергетические конфигурации одной и той же симметрии не могут пересекаться на диаграмме корреляции энергетических уровней. Короче говоря, это вызвано смешиванием состояний с одинаковой симметрией, когда они достаточно близки по энергии. Таким образом, вместо этого образуется высокий энергетический барьер между принудительным преобразованием ES-1 в ES-1 '. На диаграмме ниже предпочтительные по симметрии корреляции показаны пунктирными линиями, а жирные изогнутые линии указывают фактическую корреляцию с высоким энергетическим барьером.[14][26]

Тот же анализ можно применить к дисротационному механизму, чтобы создать следующую диаграмму корреляции состояний.[14][26]

Таким образом, если молекула находится в основном состоянии, она будет действовать по механизму вращения (т.е. под тепловым контролем), чтобы избежать электронного барьера. Однако, если молекула находится в первом возбужденном состоянии (то есть под фотохимическим контролем), электронный барьер присутствует в конротаторном механизме, и реакция будет протекать по дисротационному механизму. Они не полностью различны, поскольку и вращательные, и дисротаторные механизмы лежат на одной и той же потенциальной поверхности. Таким образом, более правильное утверждение состоит в том, что по мере того, как молекула в основном состоянии исследует поверхность потенциальной энергии, более вероятно, что она достигнет активационного барьера, чтобы пройти через конротаторный механизм.[26]
Реакции циклоприсоединения
Правила Вудворда – Гофмана также могут объяснить бимолекулярную циклоприсоединение реакции через корреляционные диаграммы.[27] A [πп + πq] циклоприсоединение объединяет два компонента, один с п π-электроны, а другой с q π-электроны. Реакции циклоприсоединения далее характеризуются как надфасциальный (s) или антарафациальный (а) по каждой из π-компонент. (См. Ниже «Общая формулировка» для подробного описания обобщения обозначения WH для всех перициклических процессов..)
[2 + 2] Циклоприсоединения
Есть 4 возможных стереохимических последствия для [2 + 2] циклоприсоединения: [π2s + π2s], [π2а + π2s], [π2s + π2а], [π2а + π2а]. Будет показано, что наиболее вероятное геометрически [π2s + π2s] режим запрещен в тепловых условиях, а режим [π2а + π2s], [π2s + π2а] подходы разрешены с точки зрения симметрии, но редки из-за неблагоприятной деформации и стерического профиля.[14] С другой стороны, [2 + 2] циклоприсоединения при фотохимической активации обычны.


Принимая во внимание [π2s + π2s] циклоприсоединение. Этот механизм приводит к сохранению стереохимии продукта, как показано справа. В исходных материалах, переходном состоянии и продукте присутствуют два элемента симметрии: σ1 и σ2. σ1 плоскость зеркала между компонентами, перпендикулярная р-орбитали; σ2 разбивает молекулы пополам перпендикулярно к σ-связи.[27] Оба эти элемента являются элементами локальной симметрии в случае, если компоненты не идентичны.

Для определения симметрии и асимметрии относительно σ1 и σ2, молекулярные орбитали исходного материала необходимо рассматривать в тандеме. На рисунке справа показана диаграмма корреляции молекулярных орбиталей для [π2s + π2s] циклоприсоединение. Два π и π* Молекулярные орбитали исходных материалов характеризуются своей симметрией относительно первой σ1 и тогда σ2. Аналогично, σ и σ* Молекулярные орбитали продукта характеризуются своей симметрией. На корреляционной диаграмме превращения молекулярных орбиталей в ходе реакции должны сохранять симметрию молекулярных орбиталей. Таким образом, πSS коррелирует с σSS, πВ КАЧЕСТВЕ коррелирует с σ*В КАЧЕСТВЕ, π*SA коррелирует с σSA, и, наконец, π*AA коррелирует с σ*AA. За счет сохранения орбитальной симметрии связывающая орбиталь πВ КАЧЕСТВЕ вынужден коррелировать с разрыхляющей орбиталью σ*В КАЧЕСТВЕ. Таким образом, прогнозируется высокий барьер.[14][26][27]
Это показано на диаграмме корреляции состояний ниже.[14][26] Основным состоянием в исходных материалах является электронное состояние, где πSS и πВ КАЧЕСТВЕ оба дважды заселены - т.е. состояние (СС)2(ТАК КАК)2. Таким образом, это состояние пытается коррелировать с электронным состоянием продукта, где как σSS и σ*В КАЧЕСТВЕ заселены дважды - т.е. состояние (СС)2(ТАК КАК)2. Однако это состояние не является основным состоянием (SS).2(SA)2 циклобутана, ни первое возбужденное состояние ES-1 '= (SS)2(SA) (AS), где электрон продвигается из HOMO в LUMO. Таким образом, основное состояние реагентов пытается коррелировать со вторым возбужденным состоянием ES-2 '= (SS)2(ТАК КАК)2.
Точно так же основное состояние производного циклобутана, как можно увидеть на диаграмме молекулярных орбиталей выше, является электронным состоянием, в котором оба σSS и σSA заселены дважды - т.е. состояние (СС)2(SA)2. Это пытается коррелировать с состоянием, в котором πSS и π*SA оба заселены дважды - то есть второе возбужденное состояние ES-2 = (SS)2(SA)2.

Наконец, первое возбужденное состояние исходных материалов - это электронная конфигурация, где πSS дважды заселен, а πВ КАЧЕСТВЕ и π*SA оба заняты поодиночке - т.е. состояние (SS)2(AS) (SA). Первым возбужденным состоянием продукта также является состояние (SS)2(SA) (AS) как σSS дважды заселен, а σSA и σ*В КАЧЕСТВЕ оба заняты поодиночке. Таким образом, эти два возбужденных состояния коррелируют.
Только основное состояние исходных материалов попытки чтобы коррелировать со вторым возбужденным состоянием, поскольку существует избежать перехода в середине из-за состояний, обладающих в целом одинаковой симметрией. Таким образом, в действительности основное состояние реагентов переходит в основное состояние продуктов только после достижения высокого энергетического барьера. Однако большого активационного барьера нет, если реагенты находятся в первом возбужденном состоянии. Таким образом, эта реакция легко протекает под фотохимическим контролем, но имеет очень высокий барьер для реакции под контролем температуры.
[4 + 2] циклоприсоединения

[4 + 2] циклоприсоединение представляет собой согласованную 2-компонентную перициклическую реакцию, примером которой является Дильс-Альдер реакция. Самый простой случай - реакция 1,3-бутадиена с этиленом с образованием циклогексена, показанная слева.
В этом преобразовании есть только один сохраняющийся элемент симметрии - плоскость зеркала, проходящая через центр реагентов, как показано слева. Отсюда мы можем очень просто определить симметрию молекулярных орбиталей реагентов. Молекулярные орбитали реагентов - это просто набор {Ψ1, Ψ2, Ψ3, Ψ4} молекулярных орбиталей 1,3-бутадиена, показанных выше, вместе с π и π* этилена. Ψ1 симметрично, Ψ2 антисимметричен, Ψ3 симметричен, а Ψ4 симметричен относительно плоскости зеркала. Аналогично π симметрична и π* антисимметричен относительно плоскости зеркала.

Молекулярные орбитали продукта представляют собой симметричную и антисимметричную комбинации двух вновь образованных σ и σ* связи и π и π* облигации, как показано ниже.
Корреляция пар орбиталей в исходных материалах и продуктах одинаковой симметрии и возрастающей энергии дает диаграмму корреляции справа. Поскольку это преобразует связывающие молекулярные орбитали в основном состоянии исходных материалов в связывающие орбитали основного состояния продукта консервативным по симметрии способом, это, как предсказывается, не будет иметь большого энергетического барьера, присутствующего в реакции основного состояния [2 + 2] выше.
Чтобы сделать анализ точным, можно построить диаграмму корреляции состояний для общего [4 + 2] -циклоприсоединения.[26] Как и прежде, основным состоянием является электронное состояние, изображенное на диаграмме корреляции молекулярных орбиталей справа. Это можно описать как Ψ12π2Ψ22, полной симметрии S2S2А2= S. Это коррелирует с основным состоянием циклогексена σSσАπ2 что также является S2S2А2= S. Как таковая, эта реакция в основном состоянии не имеет барьера, обусловленного высокой симметрией.
Можно также построить корреляции возбужденных состояний, как это сделано выше. Здесь существует высокий энергетический барьер для фотоиндуцированной реакции Дильса-Альдера под топологией супрафациально-надфасциальной связи из-за предотвращенного пересечения, показанного ниже.

Реакции группового переноса

Высота барьеров, обусловленных симметрией, реакций группового переноса также может быть проанализирована с помощью корреляционных диаграмм. Модельная реакция - это перенос пары атомов водорода от этана к пердейтериоэтану, показанный справа.
Единственным сохраняющимся элементом симметрии в этой реакции является зеркальная плоскость, проходящая через центр молекул, как показано слева.

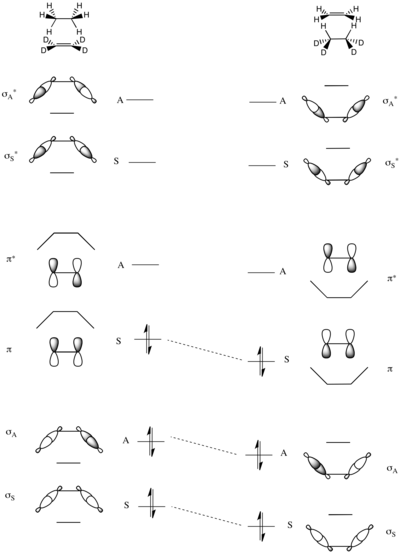
Молекулярные орбитали системы строятся как симметричные и антисимметричные комбинации σ и σ* Связи C – H в этане и π и π* связи в дейтерозамещенном этене. Таким образом, МО с наименьшей энергией представляет собой симметричную сумму двух σ-связей C – H (σS), а затем антисимметричная сумма (σА). Две МО с наивысшей энергией образуются из линейных комбинаций σCH антисвязи - наибольшее значение имеет антисимметричный σ*А, которому предшествует симметричная σ*А при немного более низкой энергии. В середине энергетической шкалы находятся две оставшиеся МО, которые представляют собой πCC и π*CC этена.
Полная диаграмма молекулярной орбитальной корреляции построена путем сопоставления пар симметричных и асимметричных МО с возрастающей полной энергией, как объяснено выше. Как можно увидеть на соседней диаграмме, поскольку связывающие орбитали реагентов точно коррелируют со связывающими орбиталями продуктов, эта реакция не имеет барьера, обусловленного высокой электронной симметрией.[14][26]
Правила отбора
Используя корреляционные диаграммы, можно вывести правила отбора для следующих обобщенных классов перициклических реакций. Каждый из этих частных классов далее обобщается в обобщенных правилах Вудворда – Хоффмана. Более инклюзивные дескрипторы топологии связи антарафациальный и надфациальный включите термины «осудительный» и «дисротативный» соответственно. Антарафациальная связь относится к образованию или разрыву связи через противоположную сторону π-системы, p-орбитали или σ-связи, в то время как супрафациальная связь относится к процессу, происходящему на той же поверхности. Супрафациальная трансформация в хиральном центре сохраняет стереохимию, тогда как антарафациальная трансформация меняет стереохимию на противоположную.
Электроциклические реакции
Правило отбора реакций электроциклизации дано в исходной формулировке правил Вудворда – Гофмана. Если обобщенное замыкание электроциклического кольца происходит в полиене 4п π-электронов, то он является вращательным в тепловых условиях и дисротационным в фотохимических условиях. И наоборот, в полиене 4п + 2 π-электронов, замыкание электроциклического кольца является дисротационным в тепловых условиях и вращательным в фотохимических условиях.
Этот результат может быть получен либо с помощью анализа FMO, основанного на знаке p-орбитальных долей HOMO полиена, либо с помощью корреляционных диаграмм. Принимая во внимание первую возможность, в основном состоянии, если полиен имеет 4п Для электронов внешние p-орбитали ВЗМО, которые образуют σ-связь в электроциклизованном продукте, имеют противоположные знаки. Таким образом, конструктивное перекрытие происходит только в процессе одновременного / антарафациального воздействия. И наоборот, для полиена с 4п + 2 электронов внешние p-орбитали ВЗМО основного состояния имеют тот же знак. Таким образом, конструктивное перекрытие орбиты происходит с дисротационным / надфасциальным процессом.[22]

Дополнительно диаграмма корреляции для любых 4п Электроциклическая реакция будет напоминать диаграмму 4-хэлектронной циклизации 1,3-бутадиена, а диаграмма корреляции любых 4п Электроциклическая реакция с 2 электронами будет напоминать корреляционную диаграмму для 6-электронной циклизации 1,3,5-гексатриена.[14]
Это обобщено в следующей таблице:
| Термически разрешено | Фотохимически разрешено | |
|---|---|---|
| 4п | соперничающий | отвратительный |
| 4п + 2 | отвратительный | соперничающий |
Сигматропные реакции перегруппировки
Общую сигматропную перегруппировку можно классифицировать как порядок [я,j], что означает, что σ-связь первоначально между атомами, обозначенными 1 и 1 ', примыкающими к одной или нескольким π-системам, смещается в положение между атомами я и j. Таким образом он мигрирует (я − 1), (j - 1) атомы от исходного положения.
Формальный анализ симметрии с помощью корреляционных диаграмм бесполезен при изучении сигматропных перегруппировок, поскольку в переходном состоянии, как правило, присутствуют только элементы симметрии. За исключением особых случаев (например, [3,3] -перестановки), нет никаких элементов симметрии, которые сохраняются при прохождении координаты реакции.[14][26] Тем не менее, орбитальные корреляции между исходными материалами и продуктами все еще могут быть проанализированы, и корреляции орбиталей исходного материала с орбиталями высокоэнергетических продуктов, как обычно, приводят к «запрещенным по симметрии» процессам. Однако подход, основанный на FMO (или анализ Дьюара-Циммермана), более прост в применении.

Один из наиболее распространенных классов сигматропных сдвигов классифицируется как [1,j], куда j странно. Это означает, что один конец σ-связи мигрирует (j - 1) связывается через π-систему, в то время как другой конец не мигрирует. Это реакция с участием j + 1 электрон: j - 1 от π-системы и 2 от σ-связи. Используя анализ FMO, [1,j] -сигматропные перегруппировки допустимы, если переходное состояние имеет конструктивное перекрытие между мигрирующей группой и принимающей p-орбиталью HOMO. В 1,j] -сигматропные перегруппировки, если j + 1 = 4п, то супра / антара термически разрешена, и если j + 1 = 4п + 2, тогда термически допустимы супра / супра или антара / антара.[26]
Другой распространенный класс сигматропных перегруппировок - это [3,3], в частности, Справиться и Claisen перестановки. Здесь конструктивные взаимодействия должны происходить между ВЗМО двух фрагментов аллильного радикала в переходном состоянии. Основное состояние HOMO Ψ2 аллильного фрагмента показан ниже. Поскольку концевые p-орбитали имеют противоположный знак, эта реакция может происходить либо в топологии супра / супра, либо в топологии антара / антара.[26]

Правила выбора для [я,j] -сигматропные перегруппировки следующие:
- Для супра / супра или антара / антара [я,j] -сигматропные сдвиги, если я + j = 4п + 2 они термически допустимы и если я + j = 4п они разрешены фотохимически
- Для supra / antara [я,j] -сигматропные сдвиги, если я + j = 4п они термически допустимы, и если я + j = 4п + 2 фотохимически разрешены
Это обобщено в следующей таблице:
| я + j | Термически разрешено | Фотохимически разрешено |
|---|---|---|
| 4п | яs + jа или же яа + js | яs + js или же яа + jа |
| 4п + 2 | яs + js или же яа + jа | яs + jа или же яа + js |
Реакции циклоприсоединения
Генерал [п+q] -циклоприсоединение - это согласованная реакция присоединения между двумя компонентами, один с п π-электроны, и один с q π-электроны. Эта реакция симметрична при следующих условиях:[14]
- Для супра / супра или антара / антара циклоприсоединения термически допустимо, если п + q = 4п + 2 и фотохимически разрешено, если п + q = 4п
- Для супра / антара циклоприсоединения это термически разрешено, если п + q = 4п и фотохимически разрешено, если п + q = 4п + 2
Это обобщено в следующей таблице:
| п + q | Термически разрешено | Фотохимически разрешено |
|---|---|---|
| 4п | пs + qа или же па + qs | пs + qs или же па + qа |
| 4п + 2 | пs + qs или же па + qа | пs + qа или же па + qs |
Реакции группового переноса
Обычная реакция двойного группового переноса, которая является синхронной, может быть представлена как взаимодействие между компонентом с п π-электронов и компонента с q π электронов, как показано.

Тогда правила отбора такие же, как и для обобщенных реакций циклоприсоединения.[14] То есть
- Для двойных групповых переводов супра / супра или антара / антара, если п + q = 4п + 2 термически допускается, а если п + q = 4п это фотохимически разрешено
- Для двойных групповых трансферов супра / антара, если п + q = 4п это термически допустимо, и если п + q = 4п + 2 фотохимически разрешено
Это обобщено в следующей таблице:
| п + q | Термически разрешено | Фотохимически разрешено |
|---|---|---|
| 4п | пs + qа или же па + qs | пs + qs или же па + qа |
| 4п + 2 | пs + qs или же па + qа | пs + qа или же па + qs |
Случай q = 0 соответствует термическому удалению "перенесенных" R-групп. Есть свидетельства того, что пиролитическое отщепление дигидрогена и этана из 1,4-циклогексадиена и 3,3,6,6-тетраметил-1,4-циклогексадиена, соответственно, представляет собой примеры этого типа перициклического процесса.
В ее реакция часто классифицируется как тип процесса группового переноса, даже если он не включает перенос двух σ-связанных групп. Напротив, переносится только одна σ-связь, в то время как вторая σ-связь образуется из разорванной π-связи. Поскольку это полностью надфазный процесс с участием 6 электронов, он является симметричным в тепловых условиях. Символ Вудворда-Хоффмана для еновой реакции [π2s + π2s + σ2s] (Смотри ниже).
Общая формулировка
Хотя правила Вудворда-Хоффмана были сначала сформулированы в терминах электроциклических процессов, в конечном итоге они были обобщены на все перициклические реакции, что должно указывать на сходство и закономерности в приведенных выше правилах отбора.

В обобщенных правилах Вудворда – Гофмана все описывается в терминах антарафациальный и надфациальный топологии связи. Условия соперничающий и отвратительный достаточны для описания относительного направления вращения связи в электроциклических реакциях замыкания или размыкания кольца, как показано справа. Однако они не подходят для описания топологий образования и разрыва связи, происходящих в общей перициклической реакции. Как подробно описано ниже, в общей формулировке правил Вудворда – Хоффмана условия вращения облигаций соперничающий и отвратительный подпадают под термины топологии (или грани) связи антарафациальный и надфасциальный, соответственно. Эти дескрипторы можно использовать для характеристики топологии образования и разрыва связи, которые имеют место в любом перициклическом процессе.
Обозначения Вудворда-Гофмана
А компонент представляет собой любую часть молекулы или молекул, которые функционируют как единое целое в перициклической реакции. Компонент состоит из одного или нескольких атомов и любого из следующих типов связанных орбиталей:
- Изолированный п- или же зрИкс-орбитальный (незаполненный или заполненный, символ ω)
- А сопряженная π система (символ π)
- А σ связь (символ σ)
В счет электронов компонента - это количество электронов на орбитали (ах) компонента:
- Счетчик электронов незаполненной ω-орбитали (то есть пустой p-орбитали) равен 0, в то время как счет заполненной ω-орбитали (то есть неподеленной пары) равен 2.
- Подсчет электронов сопряженной π-системы с п двойные связи - 2п (или 2п + 2, если к нему конъюгирована (формальная) неподеленная пара из гетероатома или карбаниона).
- Число электронов σ-связи равно 2.
В топология облигаций Компонент может быть надфасциальным и антарафациальным:
- Отношения надфасциальный (символ: s), когда взаимодействия с π-системой или p-орбиталью происходят на одной стороне узловой плоскости (подумайте син). Для связи σ это соответствует взаимодействиям, происходящим на двух «внутренних» лепестках или двух «внешних» лепестках связи.
- Отношения антарафациальный (символ: а) когда взаимодействия с π-системой или р-орбиталью происходят на противоположных сторонах узловой плоскости (подумайте анти). Для σ-связи это соответствует взаимодействиям, происходящим на одной «внутренней» доле и одной «внешней» доле связи.

Используя это обозначение, всем перициклическим реакциям можно присвоить дескриптор, состоящий из серии символов σ / π / ωNс / у, соединенные знаком + и заключенные в скобки, описывающие, по порядку, тип орбитали (орбиталей), количество электронов и топологию связи, задействованную для каждого компонента. Ниже приведены некоторые иллюстративные примеры:
- В Реакция Дильса-Альдера ((4 + 2) -циклоприсоединение) равно [π4s + π2s].
- В 1,3-диполярное циклоприсоединение из озон и олефин на первой стадии озонолиз ((3 + 2) -циклоприсоединение) равно [π4s + π2s].
- В хелетропное добавление диоксида серы в 1,3-бутадиен ((4 + 1) -хелетропное присоединение) составляет [ω0а + π4s] + [ω2s + π4s].[28]
- В Справиться перестановкой ([3,3] -сигматропный сдвиг) равен [π2s + σ2s + π2s] или [π2а + σ2s + π2а].
- [1,3] -алкильная миграция с инверсией у углерода, обнаруженная Берсон ([1,3] -сигматропный сдвиг) равен [σ2а + π2s].
- Conrotatory электроциклическое замыкание кольца 1,3-бутадиена (4π-электроциклизация) составляет [π4а].
- Conrotatory электроциклическое размыкание кольца циклобутена (обратная 4π-электроциклизация) составляет [σ2а + π2s] или [σ2s + π2а].
- Дисротативный электроциклическое замыкание кольца 1,3-циклооктадиен-5-ид-аниона (6π-электроциклизация) представляет собой [π6s].
- А Сдвиг Вагнера-Меервейна из карбокатион ([1,2] -сигматропный сдвиг) равен [ω0s + σ2s].
Антарафациальная и супрафациальная зоны связаны с (вращением / инверсией) и (разворотом / удержанием) соответственно. Один дескриптор может соответствовать двум перициклическим процессам, которые химически различны, что реакция и ее микроскопическая обратная сторона часто описываются двумя разными дескрипторами, и что один процесс может иметь более одного правильного дескриптора. Используя приведенное ниже правило перициклического отбора, можно проверить, что все эти реакции являются разрешенными процессами.
Оригинальное заявление
Используя эти обозначения, Вудвард и Хоффманн в своем обзоре 1969 года формулируют общую формулировку всех перициклических реакций следующим образом:
Перициклическое изменение основного состояния допустимо по симметрии, когда общее количество (4q + 2)s и (4r)а компоненты нечетные.[14]
Здесь (4q + 2)s и (4р)а см. супрафациальные (4q + 2) -электронно-антарафациальный (4р) -электронные компоненты соответственно. Причем этот критерий следует интерпретировать как достаточно (указано выше), а также необходимо (явно не указано выше, видеть: если и только если )
Вывод альтернативного заявления
В качестве альтернативы, общее утверждение можно сформулировать в терминах Всего количество электронов с использованием простых правил деления путем прямого анализа двух случаев.
Сначала рассмотрим случай, когда общее количество электронов равно 4.п + 2. Тогда мы можем написать
- 4п + 2 = а(4q + 2)s + б(4п + 2)а + c(4т)s + d(4р)а,
куда а, б, c, и d - коэффициенты, указывающие количество компонентов каждого типа. Это уравнение подразумевает, что одно, но не оба, а или же б нечетно, потому что если а и б оба четные или оба нечетные, тогда сумма четырех членов равна 0 (mod 4).
Обобщенная формулировка правил Вудворда – Хоффмана утверждает, что а + d является нечетным, если реакция разрешена. Сейчас если а четно, то отсюда следует, что d странно. С б в данном случае нечетное количество антарафациальных компонентов, б + d, даже. Аналогично, если а странно, то d даже. С б даже в этом случае количество антарафациальных компонентов, б + d, снова даже. Таким образом, независимо от исходного предположения о четности для а и б, количество антарафациальных компонентов равно даже при подсчете электронов 4п + 2. Наоборот, в запрещенном случае, когда а + г четно, мы можем показать, что, независимо от исходных предположений, б + d странно.
В случае, когда общее количество электронов равно 4п, аналогичные аргументы (здесь опущены) приводят нас к выводу, что количество антарафациальных компонентов б + d должно быть нечетным в разрешенном случае и даже в запрещенном.
Наконец, чтобы завершить рассуждение и показать, что этот новый критерий действительно эквивалентен исходному критерию, необходимо также аргументировать обратные утверждения, а именно, что количество антарафациальных компонентов б + d и счет электронов (4п + 2 или 4п) следует четность а + d который задается правилами Вудворда – Хоффмана (нечетное для разрешенного, четное для запрещенного). Еще один раунд (несколько утомительного) анализа случаев легко покажет, что это так.
Подводя итог, у нас есть следующее утверждение, которое математически эквивалентно исходному обобщенному перициклическому правилу выбора:
Перициклический процесс с участием 4n + 2 или 4n электронов термически разрешен тогда и только тогда, когда количество задействованных антарафациальных компонентов является четным или нечетным, соответственно.
| Hückel | Мебиус | |
|---|---|---|
| 4п+2 e– | Позволил ароматный | Запрещенный антиароматический |
| 4п е– | Запрещенный антиароматический | Позволил ароматный |
В этой формулировке счет электронов относится ко всей реагирующей системе, а не к отдельным компонентам, как указано в первоначальном заявлении Вудворда и Хоффмана. На практике четное или нечетное количество антарафациальных компонентов обычно означает ноль или один антарафациальный компонент, соответственно, поскольку переходные состояния с участием двух или более антарафациальных компонентов обычно не благоприятствуют деформации. В качестве исключения, определенные внутримолекулярные реакции могут быть геометрически ограничены таким образом, чтобы обеспечить антарафациальную траекторию для нескольких компонентов. Кроме того, в некоторых случаях, например, при перегруппировке Коупа, одна и та же (не обязательно напряженная) геометрия переходного состояния может рассматриваться как содержащая два супра- или два антра-π-компонента, в зависимости от того, как проводится связь между лепестками орбиты. (Эта неоднозначность является следствием соглашения, согласно которому перекрытие обеих внутренних или обеих внешних долей σ-компонента можно рассматривать как надфазное.)
Эта альтернативная формулировка делает очевидной эквивалентность правил Вудворда – Хоффмана анализу Дьюара – Циммермана (см. Ниже). Четное общее количество фазовых инверсий эквивалентно четному количеству антарафациальных компонентов и соответствует топологии Хюккеля, требующей 4п + 2 электрона для ароматичности, в то время как нечетное общее количество фазовых инверсий эквивалентно нечетному количеству антарафациальных компонентов и соответствует топологии Мёбиуса, требующей 4п электроны на ароматичность.[29] Подводя итог теории ароматических переходных состояний: Термический перициклический реакции протекают через (4п + 2)-электрон Хюккель или (4п)-электронные переходные состояния Мёбиуса.
В качестве мнемоники приведенную выше формулировку можно переформулировать следующим образом:
Перициклический процесс в основном состоянии с участием N электронных пар и A антарафациальных компонентов является симметричным тогда и только тогда, когда N + A нечетно.
Альтернативное доказательство эквивалентности
Эквивалентность этих двух формулировок также можно увидеть с помощью простого аргумента о четности без обращения к анализу случаев.
Предложение. Следующие формулировки правил Вудворда – Хоффмана эквивалентны:
(А) Для перициклической реакции, если сумма количества супрафациальных 4q + 2 компонентов и антарафациальных 4r компонентов нечетная, то это термически допустимо; в противном случае реакция термически запрещена.
(В) Для перициклической реакции, если общее количество антарафациальных компонентов (4n + 2) -электронной реакции четное или общее количество антарафациальных компонентов 4n-электронной реакции нечетное, то это термически разрешено; в противном случае реакция термически запрещена.
Доказательство эквивалентности: Проиндексируйте компоненты k-компонентная перициклическая реакция и назначить компонент я с символом Вудворда-Гофмана σ / π / ωNс / у символ количества электронов и топологической четности по следующим правилам:
У нас есть математически эквивалентное повторение (А):
(А ') Коллекция символов термически разрешено тогда и только тогда, когда количество символов со свойством странно.
Поскольку общее количество электронов равно 4п + 2 или 4п именно когда (количество (4q + 2) -электронные компоненты) нечетные или четные соответственно, а дает количество антарафациальных компонентов, мы также можем пересчитать (В):
(B ') Коллекция символов термически допустимо тогда и только тогда, когда ровно одно из или же странно.
Достаточно показать, что (А ') и (B ') эквивалентны. Ровно один из или же нечетно тогда и только тогда, когда странно. Если , держит; следовательно, пропуск символов со свойством из коллекции не изменит четность . С другой стороны, когда , у нас есть , но просто перечисляет количество компонентов с помощью свойства . Следовательно,
.
Таким образом, и количество символов в коллекции со свойством имеют такой же паритет. Поскольку составы (А ') и (B ') эквивалентны, так же (А) и (В), как утверждается. □
Чтобы привести конкретный пример, гипотетическая реакция с дескриптором [π6s + π4а + π2а] будет назначен набор {(1, 0, 1), (0, 1, 2), (1, 1, 3)} в схеме выше. Есть два компонента (1, 0, 1) и (0, 1, 2) со свойством , поэтому реакция не допускается (А '). Точно так же и оба четные, так что (B ') приводит к тому же выводу (как и должно): реакция недопустима.
Примеры
Эта формулировка для двухкомпонентной реакции эквивалентна правилам выбора для [п + q] реакции -циклоприсоединения показаны в следующей таблице:
| р + д | Термически разрешено | Фотохимически разрешено |
|---|---|---|
| 4п | пs + qа или же па + qs | пs + qs или же па + qа |
| 4п + 2 | пs + qs или же па + qа | пs + qа или же па + qs |
Если общее количество электронов равно 4п + 2, то единица находится в нижней строке таблицы. Реакция термически разрешена, если она является супрафациальной по отношению к обоим компонентам или антарафациальной по отношению к обоим компонентам. То есть количество антарафациальных компонентов четное (0 или 2). Аналогично, если общее количество электронов равно 4п, то один находится в верхней строке таблицы. Это допустимо с термической точки зрения, если оно является супрафациальным по отношению к одному компоненту и антарафациальным по отношению к другому. Таким образом, общее количество антарафациальных компонентов всегда нечетное, поскольку оно всегда равно 1.
Ниже приведены некоторые общие классы реакций в основном состоянии (т. Е. Термические), проанализированные в свете обобщенных правил Вудворда – Хоффмана.
[2 + 2] Циклоприсоединение
[2 + 2] -циклоприсоединение - это четырехэлектронный процесс, который объединяет два компонента. Таким образом, согласно приведенным выше общим правилам WH, это разрешено только в том случае, если реакция является антарафациальной по отношению только к одному компоненту. К такому же выводу пришли корреляционные диаграммы в предыдущем разделе.
Редкий, но стереохимически однозначный пример [π2s + π2а] -циклоприсоединение показано справа. Деформационные и стерические свойства транс двойная связь делает возможным этот обычно кинетически неблагоприятный процесс. СНГ, трансСчитается, что -1,5-Циклооктадиен также подвергается димеризации в этом режиме.[14] Кетены представляют собой большой класс реагентов, способствующих [2 + 2] циклоприсоединению к олефинам. МО анализ циклоприсоединение кетена усложняется и неоднозначно из-за одновременного, но независимого взаимодействия ортогональных орбиталей кетена, но может включать [π2s + π2а] взаимодействие.[30]
[4 + 2] Циклоприсоединение
Синхронный 6π-электрон Дильс-Альдер реакция - это [π4s + π2s] -циклоприсоединение (т.е. супрафациальное по отношению к обоим компонентам), как показано на примере реакции справа.

Таким образом, поскольку общее количество антарафациальных компонентов равно 0, что является четным, реакция разрешена по симметрии.[14] Это предсказание согласуется с экспериментом, так как реакция Дильса-Альдера является довольно простой перициклической реакцией.
4п Электроциклическая реакция
А 4п Реакция электронного электроциклического раскрытия кольца может рассматриваться как имеющая 2 компонента - π-систему и разрыв σ-связи. По отношению к π-системе реакция надфазна. Однако при конротаторном механизме, как показано на рисунке выше, реакция является антарафациальной по отношению к σ-связи. Напротив, при дисротационном механизме он является супрафациальным по отношению к разрыву σ-связи.
По указанным выше правилам для 4п электронная перициклическая реакция 2 компонентов, должен быть один антарафациальный компонент. Таким образом, реакция должна протекать по механизму вращения.[14] Это согласуется с результатом, полученным на корреляционных диаграммах выше.
4п + 2 электроциклические реакции
А 4п + 2 реакция электроциклического раскрытия кольца также является 2-компонентной перициклической реакцией, которая является надациальной по отношению к π-системе. Таким образом, для того, чтобы реакция была разрешена, количество антарафациальных компонентов должно быть равно 0, то есть они должны быть супрафациальными по отношению к разрыву σ-связи. Таким образом, дисротационный механизм допустим по симметрии.[14]
[1,j] -сигматропная перегруппировка

A [1,j] -сигматропная перегруппировка также является двухкомпонентной перициклической реакцией: один компонент представляет собой π-систему, другой компонент - мигрирующую группу. Самый простой случай - это [1,j] -гидридный сдвиг по π-системе, где j странно. В этом случае, поскольку водород имеет только сферически-симметричную s-орбиталь, реакция должна быть надациальной по отношению к водороду. Общее количество вовлеченных электронов (j + 1) как есть (j - 1) / 2 π-связь плюс σ-связь, участвующая в реакции. Если j = 4п - 1 тогда он должен быть антарафациальным, а если j = 4п +1, то он должен быть надфасциальным.[14] Это согласуется с экспериментом, согласно которому сдвиги [1,3] -гидрида обычно не наблюдаются, поскольку разрешенный симметрией антарафациальный процесс невозможен, но сдвиги [1,5] -гидрида довольно легки.
Для [1,j] -алкильный сдвиг, когда реакция может быть антарафациальной (т.е. инвертировать стереохимию) по отношению к углеродному центру, применяются те же правила. Если j = 4п - 1, то реакция симметрична, если она либо антарафациальна по отношению к π-системе, либо инвертирует стереохимию у углерода. Если j = 4п + 1, то реакция разрешена по симметрии, если она надфазна по отношению к π-системе и сохраняет стереохимию в углеродном центре.[14]
Справа - один из первых обнаруженных примеров [1,3] -сигматропного сдвига, о котором сообщил Берсон в 1967 г.[31] Чтобы обеспечить инверсию конфигурации при разрыве σ-связи, фрагмент C (H) (D) закручивается в переходном состоянии, при этом гибридизация углерода приближается к sp2, так что оставшаяся негибридизированная p-орбиталь сохраняет перекрытие с обоими атомами углерода 1 и 3.
Эквивалентность других теоретических моделей
Анализ Дьюара – Циммермана

Обобщенные правила Вудворда – Хоффмана, впервые введенные в 1969 г., эквивалентны более раннему общему подходу, Концепция Мебиуса-Хюккеля Циммермана, который был впервые заявлен в 1966 году и также известен как теория ароматических переходных состояний.[15][32][33] В качестве своего центрального принципа теория ароматических переходных состояний утверждает, что «разрешенные» перициклические реакции протекают через переходные состояния с ароматическим характером, в то время как «запрещенные» перициклические реакции будут сталкиваться с переходными состояниями, которые являются антиароматическими по своей природе. В анализе Дьюара-Циммермана речь идет о топологии переходного состояния перициклической реакции. Если в переходном состоянии участвует 4п электронов, топология Мёбиуса является ароматической, а топология Хюккеля - антиароматической, в то время как если в переходном состоянии участвует 4п + 2 электронов топология Хюккеля является ароматической, а топология Мебиуса антиароматической. Четность количества фазовые инверсии (подробно описано ниже) в переходном состоянии определяет его топологию. Топология Мёбиуса включает в себя странный количество инверсий фазы, тогда как топология Хюккеля включает даже количество инверсий фазы.

В связи с терминологией Вудворда – Хоффмана количество антарафациальных компонентов и количество фазовых инверсий всегда имеют одинаковую четность.[29] Следовательно, нечетное число антарафациальных компонентов дает топологию Мебиуса, а четное число дает топологию Хюккеля. Таким образом, чтобы переформулировать результаты теории ароматических переходных состояний на языке Вудворда и Хоффмана, необходимо 4п-электронная реакция термически разрешена тогда и только тогда, когда она имеет нечетное число антарафациальных компонентов (то есть топология Мёбиуса); а (4п + 2) -электронная реакция термически разрешена тогда и только тогда, когда она имеет четное число антарафациальных компонентов (то есть топология Хюккеля).
Процедура анализа Дьюара-Циммермана (примеры показаны справа): Шаг 1. Затенение всех базисных орбиталей, входящих в перициклическую систему. Оттенок может быть произвольным. В частности, затенение не обязательно должно отражать фазирование полиеновых МО; каждая базисная орбиталь просто должна иметь два противоположно фазированных лепестка в случае p или spИкс гибридные орбитали или однофазные в случае s-орбитали. Шаг 2. Нарисуйте связи между лепестками базисных орбиталей, которые геометрически хорошо расположены для взаимодействия в переходном состоянии. Установленные соединения зависят от топологии переходного состояния. (Например, на рисунке показаны разные соединения в случаях кон- и дисротационной электроциклизации.) Шаг 3. Подсчитайте количество соединений, которые возникают между лепестками противоположного затенения: каждое из этих соединений представляет собой инверсию фазы. Если количество фазовых инверсий четное, переходное состояние - Хюккелевское, а если количество фазовых инверсий нечетное, то переходное состояние - Мебиус. Шаг 4. Сделайте вывод, что перициклическая реакция разрешена, если количество электронов равно 4.п + 2, а переходное состояние - Хюккель, или, если количество электронов равно 4п и переходное состояние - Мебиус; в противном случае заключают, что перициклическая реакция запрещена.
Важно отметить, что приемлема любая схема присвоения относительных фаз базисным орбиталям, поскольку инвертирование фазы любой отдельной орбитали добавляет 0 или ± 2 инверсии фазы к общему четному числу, так что паритет количества инверсий (количество инверсий по модулю 2) без изменений.
Переосмысление концептуальной теории функционала плотности
Недавно правила Вудворда – Хоффмана были переосмыслены с использованием концептуального подхода. теория функционала плотности (ДПФ).[6][34] Ключом к анализу является функция двойного дескриптора, предложенная Кристофом Мореллем, Андре Грандом и Алехандро Торо-Лаббе.[35] , вторая производная электронной плотности по количеству электронов . Эта функция отклика важна, так как реакция двух компонентов A и B, включающая перенос электронов, будет зависеть от чувствительности электронной плотности к передаче или принятию электронов, то есть производной функции Фукуи . Фактически, с упрощенной точки зрения, функция двойного дескриптора дает информацию об электрофильности или нуклеофильности различных областей молекулы. За область электрофильная, а для , область является нуклеофильной. Используя предположение о границе молекулярной орбиты и аппроксимацию конечными разностями функции Фукуи, можно записать дуальный дескриптор как
Это имеет интуитивно понятный смысл, так как если область лучше принимает электроны, чем жертвует, тогда LUMO должен доминировать, и функция двойного дескриптора будет положительной. И наоборот, если область лучше отдаёт электроны, тогда член HOMO будет доминировать, а дескриптор будет отрицательным. Обратите внимание: хотя понятие фазы и орбиталей заменено просто понятием электронной плотности, эта функция по-прежнему принимает как положительные, так и отрицательные значения.

Правила Вудворда-Хоффмана интерпретируются заново с использованием этой формулировки путем сопоставления благоприятных взаимодействий между областями электронной плотности, для которых дуальный дескриптор имеет противоположные знаки. Это эквивалентно максимизации предсказанных благоприятных взаимодействий и минимизации отталкивающих взаимодействий. Для случая [4 + 2] циклоприсоединения упрощенная схема реагентов с функцией двойного дескриптора, окрашенной (красный = положительный, синий = отрицательный), показана в оптимальной над / над-конфигурации слева. Этот метод правильно предсказывает правила WH для основных классов перициклических реакций.
Исключения
В главе 12 Сохранение орбитальной симметрииВудворд и Хоффманн под названием «Нарушения» заявили:
Нет! Нельзя также ожидать нарушений столь фундаментального принципа максимальной связи.
Несмотря на это заявление, важно понимать, что правила Вудворда-Хоффмана используются для предсказания относительной высоты барьеров и, следовательно, вероятных механизмов реакции, и что они учитывают только барьеры, обусловленные сохранением орбитальной симметрии. Таким образом, не гарантируется, что реакция, допускаемая симметрией WH, действительно имеет место легко. И наоборот, при достаточной энергии можно получить продукт, направленный против Вудворда-Хоффмана. Это особенно распространено в стерически ограниченных системах, где WH-продукт имеет дополнительный стерический барьер, который необходимо преодолеть. Например, при электроциклическом раскрытии кольца производного диметилбицикло [0.2.3] гептена (1), вращательный механизм невозможен из-за возникающей угловой деформации, и реакция протекает медленно через дисротационный механизм при 400о C с получением циклогептадиенового продукта.[22] Нарушения могут также наблюдаться в случаях очень сильных термодинамических движущих сил. Разложение диоксетан-1,2-дион до двух молекул углекислого газа, известного своей ролью в люминесценции светящиеся палочки, был тщательно исследован с помощью вычислений. В отсутствие флуоресценции, теперь считается, что реакция протекает согласованным (хотя и асинхронным) образом, через ретро- [2 + 2] -циклоприсоединение, которое формально нарушает правила Вудворда-Хоффмана.[36]


Точно так же в недавней статье описывается, как механическое напряжение могут быть использованы для изменения путей химических реакций, чтобы приводить к продуктам, которые явно нарушают правила Вудворда-Хоффмана.[37] В этой статье они используют ультразвуковое облучение для создания механического напряжения на функционализированных связями полимерах, прикрепленных син- или анти-синфазно к циклобутеновому кольцу. Вычислительные исследования предсказывают, что механическая сила, возникающая в результате трения полимеров, вызывает удлинение связи вдоль координаты реакции вращательного механизма в антибисамещенном циклобутене и вдоль координаты реакции дисротационного механизма в син-бисзамещенном циклобутене. . Таким образом, в син-бисзамещенном циклобутене анти-Прогнозируется образование продукта.
Это расчетное предсказание было подтверждено экспериментом с системой ниже. Полимеры с функциональными связями конъюгировали с СНГ бензоциклобутен как в син-, так и в антиконформации. Как и предполагалось, оба продукта давали один и тот же продукт (Z, Z), как было определено путем гашения стереоспецифической реакцией Дильса-Альдера с замещенным малеимидом. В частности, син-замещенный продукт давал продукт анти-WH, предположительно, поскольку механическое растяжение вдоль координаты дисротационного пути понижало барьер реакции в дисротационном пути настолько, чтобы смещать этот механизм.

Полемика
Было заявлено, что Элиас Джеймс Кори, также лауреат Нобелевской премии, считает, что несет ответственность за идеи, которые легли в основу этого исследования, и что Вудворд несправедливо пренебрег его открытием. В мемуарах 2004 г., опубликованных в Журнал органической химии,[38] Кори заявляет о приоритете идеи: «4 мая 1964 года я предложил своему коллеге Р. Б. Вудворду простое объяснение, включающее симметрию возмущенных (ВЗМО) молекулярных орбиталей стереоселективного циклобутена по отношению к 1,3-бутадиену и 1 , Превращения 3,5-гексатриена в циклогексадиен, которые послужили основой для дальнейшего развития этих идей в то, что стало известно как правила Вудворда-Хоффмана ».
Кори, которому тогда было 35 лет, работал до вечера в понедельник, 4 мая, как это часто делали он и другие химики. Примерно в 20:30 он зашел в офис Вудворда, и Вудворд задал вопрос о том, как предсказать тип кольца, которое образует цепочка атомов. После некоторого обсуждения Кори предположил, что конфигурация электронов определяет ход реакции. Вудворд настаивал, что решение не сработает, но Кори оставил чертежи в офисе, будучи уверенным, что он что-то понимает.[39]
«Я чувствовал, что это будет действительно интересное событие, и с нетерпением ждал какого-то совместного предприятия», он написал. Но на следующий день Вудворд прилетел в офис Кори, когда они с коллегой уходили на обед, представил идею Кори как свою собственную - а затем ушел. Кори был ошеломлен.
В опровержении 2004 г., опубликованном в Angewandte Chemie,[40] Роальд Хоффманн отрицал это утверждение: он цитирует Вудворда из лекции, прочитанной в 1966 году, в которой говорится: «Я ПОМНИТЕ очень ясно - и это все еще меня несколько удивляет, - что решающая вспышка просветления пришла ко мне в алгебраической, а не в изобразительной или геометрической форме. Совершенно неожиданно мне пришло в голову, что коэффициенты конечных членов в математическое выражение, представляющее самую высокую занятую молекулярную орбиталь бутадиена, имело противоположный знак, в то время как выражения соответствующего выражения для гексатриена имели тот же знак. Отсюда был лишь небольшой шаг к геометрическому и, что более очевидно, химически значимому взгляду, что в При внутренней циклизации диена верхняя грань одного концевого атома должна атаковать нижнюю грань другого, в то время как в случае триена образование новой связи должно охватывать верхние (или pari passu, нижние) грани обоих концевые атомы ".
Кроме того, Хоффманн указывает, что в двух публикациях 1963 г.[41] и 1965 г.,[42] Кори описал полный синтез соединения дигидрокостунолида. Хотя они описывают электроциклическую реакцию, Кори не может предложить ничего, чтобы объяснить стереоспецифичность синтеза.
Этот фотохимический реакция с участием 6 = 4 × 1 + 2 электронов теперь признана конротаторной.
Смотрите также
- Правила Вудворда для расчета поглощения УФ
- Торкоселективность
Рекомендации
- ^ Принцип сохранения орбитальной симметрии обычно приписывают Роберт Бернс Вудворд и Роальд Хоффманн, который предложил сохранение орбитальной симметрии как объяснение стереохимического исхода электроциклических реакций (Варенье. Chem. Soc. 1965, 87, 395) и сформулировал полностью обобщенное перициклическое правило отбора несколько лет спустя (Энгью. Chem. Int. Эд. Англ. 1969, 8, 781). Тем не мение, Э. Дж. Кори заявил о приоритете в предложении ключевой идеи в 1965 г. (см. раздел «Противоречие» ниже). Более того, Э. Хавинга ранее отмечал, что тахистерин подвергается электроциклическому замыканию кольца одновременно или дисротационным образом в зависимости от режима активации (фотохимический или термический, соответственно), и приписывал объяснение орбитальной симметрии этого явления L. J. Oosterhoff (Tetrahedron Lett. 1961, 16, 146). Кроме того, теория ароматических переходных состояний, продвинутый Х. Э. Циммерман (Варенье. Chem. Soc. 1966, 88, 1564) и М. Дж. С. Дьюар (Тетраэдр 1966, Дополнение 8, 75), был признан альтернативным подходом, который полностью эквивалентен, но предшествует формулировке обобщенного правила Вудворда и Хоффмана.
- ^ П. Р. Банкер и П. Дженсен (2005),Основы молекулярной симметрии (CRC Press)ISBN 0-7503-0941-5[1]
- ^ Реакции Ene часто считают типом реакции переноса группы.
- ^ Хелетропные реакции часто считают типом циклоприсоединения.
- ^ Ритц, Манфред Т. (1972-02-01). "Диотропные перегруппировки, новый класс реакций, контролируемых орбитальной симметрией. Тип I". Angewandte Chemie International Edition на английском языке. 11 (2): 129–130. Дои:10.1002 / anie.197201291. ISSN 1521-3773.
- ^ а б Герлингс, Пол; Эйерс, Пол У .; Торо-Лаббе, Алехандро; Chattaraj, Pratim K .; Де Профт, Франк (2012). "Правила Вудворда-Хоффмана, переосмысленные функциональной теорией концептуальной плотности". Отчеты о химических исследованиях. 45 (5): 683–95. Дои:10.1021 / ar200192t. PMID 22283422.
- ^ Нобелевская премия по химии 1981 г.. Nobelprize.org.
- ^ Правила Вудворда – Хоффмана применимы к любому направлению перициклического процесса. Из-за присущей производным циклобутена кольцевой деформации равновесие между циклобутеном и 1,3-бутадиеном лежит далеко вправо. Следовательно, в термических условиях раскрытие цикла циклобутена в 1,3-бутадиен сильно поддерживается термодинамикой. С другой стороны, при облучении ультрафиолетом фотостационарное состояние достигается состав, который зависит как от поглощения, так и от квантового выхода прямой и обратной реакций на определенной длине волны. Из-за разной степени конъюгации 1,3-бутадиенов и циклобутенов только 1,3-бутадиен будет иметь значительную оптическую плотность на более высоких длинах волн, при условии отсутствия других хромофоров. Следовательно, облучение 1,3-бутадиена на такой длине волны может привести к высокой конверсии в циклобутен.
- ^ Криджи, Рудольф; Нолл, Клаус (1959). "Umsetzungen in der Reihe des 1.2.3.4-Tetramethyl-cyclobutans". Юстус Либигс Аннален дер Хеми. 627: 1–14. Дои:10.1002 / jlac.19596270102.
- ^ Хотя на рисунке ниже показаны оба конца, вращающиеся по часовой стрелке, важно понимать, что орбитальная симметрия различает только вращение в одном и том же направлении или в противоположных направлениях (сочувствие против. развращение).Формирование (Z,Z) изомер от раскрытия кольца 1 (оба конца вращаются против часовой стрелки), следовательно, также допускается симметрия. Это (Z,Z) изомер не наблюдался, вероятно, из-за неблагоприятных стерических взаимодействий между вращающимися внутрь метильными группами. (В других случаях предпочтение вращения облигаций по часовой стрелке или против часовой стрелки может контролироваться стереоэлектронными факторами: видеть торкоселективность.)
- ^ Сринивасан, Р. (1968-07-01). «Механизм фотохимической валентной таутомеризации 1,3-бутадиенов». Журнал Американского химического общества. 90 (16): 4498–4499. Дои:10.1021 / ja01018a080. ISSN 0002-7863.
- ^ Винтер, Рудольф Эрнст К. (1965-01-01). «Получение и изомеризация цис- и транс-3,4-диметилциклобутена». Буквы Тетраэдра. 6 (17): 1207–1212. Дои:10.1016 / S0040-4039 (01) 83997-6. ISSN 0040-4039.
- ^ Исходное утверждение, данное Вудвордом и Хоффманном, несколько более детально:Перициклическое изменение основного состояния допустимо по симметрии, когда общее количество (4q + 2)s и (4r)а компоненты нечетные.Однако приведенное здесь утверждение математически эквивалентно. Для доказательства см .: https://archive.org/details/whdz_red
- ^ а б c d е ж грамм час я j k л м п о п q р s т ты v Woodward, R. B .; Хоффманн, Роальд (1969). «Сохранение орбитальной симметрии». Энгью. Chem. Int. Эд. 8 (11): 781–853. Дои:10.1002 / anie.196907811.
- ^ а б Циммерман, Х. Э. (1966). "О диаграммах молекулярной орбитальной корреляции, появлении систем Мебиуса в реакциях циклизации и факторах, управляющих реакциями основного и возбужденного состояний. I". Журнал Американского химического общества. 88 (7): 1564–1565. Дои:10.1021 / ja00959a052.
- ^ Циммерман, Ховард Э. (1971-08-01). «Концепция Мебиуса-Хюккеля в органической химии. Применение органических молекул и реакций». Отчеты о химических исследованиях. 4 (8): 272–280. Дои:10.1021 / ar50044a002. ISSN 0001-4842.
- ^ Дьюар, M.J.S. (1966-01-01). "Теория молекулярных орбиталей органической химии - VIII: романтичность и электроциклические реакции". Тетраэдр. 22: 75–92. Дои:10.1016 / S0040-4020 (01) 82171-2. ISSN 0040-4020.
- ^ Дьюар, Майкл Дж. С. (1971-11-01). «Ароматичность и перициклические реакции». Angewandte Chemie International Edition на английском языке. 10 (11): 761–776. Дои:10.1002 / anie.197107611. ISSN 1521-3773.
- ^ Фукуи, Кеничи (1965-01-01). «Стереоселективность, связанная с нециклоприсоединением к ненасыщенным связям». Буквы Тетраэдра. 6 (28): 2427–2432. Дои:10.1016 / S0040-4039 (00) 90203-X. ISSN 0040-4039.
- ^ Фукуи, Кеничи (1982). «Роль пограничных орбиталей в химических реакциях». Наука. 218 (4574): 747–754. Bibcode:1982Наука ... 218..747F. Дои:10.1126 / наука.218.4574.747. JSTOR 1689733. PMID 17771019.
- ^ Точнее, система с «запрещенной симметрией» с истинной симметрией имеет связывающие орбитали исходного материала, которые коррелируют с антисвязывающими орбиталями продукта и наоборот. Напротив, когда заместитель нарушает симметрию, эти пересечения уровней «едва избегаются» уровнями энергии, которые приближаются (около переходного состояния), но затем расходятся. В отличие от разницы в орбитальный корреляционные диаграммы, государственный диаграммы корреляции всегда имеют «едва избегаемые» пересечения, независимо от того, является ли симметрия «истинной» или «приблизительной». Таким образом, наличие или отсутствие простого заместителя, который нарушает формальный элемент симметрии, несущественно, поскольку диаграмма корреляции состояний не изменяется в качественном смысле. Повышение энергии основного состояния по мере приближения к «едва избегаемому» пересечению приводит к наложенному симметрией энергетическому барьеру в переходном состоянии.
- ^ а б c Woodward, R. B .; Хоффманн, Роальд (1965). «Стереохимия электроциклических реакций». Журнал Американского химического общества. 87 (2): 395. Дои:10.1021 / ja01080a054.
- ^ Longuet-Higgins, H.C .; Абрахамсон, Э. У. (1965). «Электронный механизм электроциклических реакций». Журнал Американского химического общества. 87 (9): 2045. Дои:10.1021 / ja01087a033.
- ^ Woodward, R. B .; Хоффманн, Роальд (1971). Сохранение орбитальной симметрии (3-е издание, 1-е изд.). Weinheim, BRD: Verlag Chemie GmbH (BRD) и Academic Press (США). С. 1–178. ISBN 978-1483256153.
- ^ П. Р. Банкер и П. Дженсен (2005), Основы молекулярной симметрии (CRC Press) ISBN 0-7503-0941-5[2] см. раздел 10.4
- ^ а б c d е ж грамм час я j k Кэрролл, Феликс (1998) Перспективы структуры и механизма в органической химии, Brooks / Cole, стр. 710–794, ISBN 0534249485.
- ^ а б c Хоффманн, Роальд; Вудворд, Р. Б. (1965). «Правила выбора для согласованных реакций циклоприсоединения». Варенье. Chem. Soc. 87 (9): 2046. Дои:10.1021 / ja01087a034.
- ^ Потому что ТАК2 имеет ортогональную неподеленную пару и разрыхляющие орбитали (аллилподобная разрыхляющая орбиталь SO2 здесь анализируется как простая незанятая p-орбиталь), взаимодействие этих орбиталей с орбиталями 1,3-бутадиена необходимо анализировать отдельно. В общем, для такого сложного процесса, как эта хелетропная реакция, обе отдельных орбитальных взаимодействий необходимо учитывать, чтобы реакция была разрешена. Подход FMO, вероятно, дает здесь наиболее интуитивную картину.
- ^ а б Чтобы понять, почему это так, мы утверждаем, что всегда можно произвести анализ Дьюара-Циммермана максимум с одной фазовой инверсией и что результат зависит от четности количества антарафациальных компонентов. Мы начинаем с произвольного затенения первой орбитали любого компонента и завершаем затемнение остальной части компонента, чтобы внутри него не происходило инверсии фазы. Мы проводим связи Дьюара-Циммермана между компонентами на основе топологии связи (выше или же Антара) каждого компонента. Используя эти соединения, можно продолжить затенение на соседних компонентах, чтобы не было инверсии между компонентами или внутри компонента. Это продолжается до тех пор, пока все взаимодействующие орбитали не будут заштрихованы, и для завершения цикла потребуется только последнее соединение Дьюара-Циммермана. До этого момента инверсия фазы не применялась. Важное наблюдение: связи Дьюара-Циммермана, идущие от двух концов антарафациального (надфациального) компонента к соседним компонентам, будут соединять доли противоположного (одинакового) затенения.. Следовательно, нечетное количество антарафациальных компонентов вызовет однофазную инверсию для завершения цикла, в то время как четное количество антарафациальных компонентов позволит завершить цикл без инверсии фазы. Поскольку количество инверсий (по модулю 2) инвариантно относительно орбитальной фазировки, эти две возможности (нечетное или четное количество антарафациальных компонентов) определяют, есть ли у нас система Мебиуса (одна инверсия) или Хюккеля (без инверсии) соответственно. .
- ^ Ямабе, Шиничи; Кувата, Кайоко; Минато, Цутому (1999). «Погранично-орбитальный анализ циклоприсоединений кетена [2 + 2]». Счета теоретической химии: теория, вычисления и моделирование (Theoretica Chimica Acta). 102 (1–6): 139–146. Дои:10.1007 / s002140050484.
- ^ Берсон, Джером А .; Нельсон, Джордж Л. (1967-10-01). «Инверсия конфигурации в мигрирующей группе термической 1,3-сигматропной перегруппировки». Журнал Американского химического общества. 89 (21): 5503–5504. Дои:10.1021 / ja00997a065. ISSN 0002-7863.
- ^ Циммерман, Х. Э. (1966). "О диаграммах молекулярной орбитальной корреляции, системах Мебиуса и факторах, контролирующих реакции земли и возбужденного состояния. II". Варенье. Chem. Soc. 88 (7): 1566–156. Дои:10.1021 / ja00959a053.
- ^ Циммерман, Х. Э. (2006). «Пять десятилетий механистической и исследовательской органической фотохимии». Pure Appl. Chem. 78 (12): 2193–2203. Дои:10.1351 / pac200678122193.
- ^ Эйерс, Пол У .; Морелл, Кристоф; Де Профт, Франк; Герлингс, Пол (5 октября 2007 г.). «Понимание правил Вудворда-Гофмана с помощью изменений электронной плотности». Химия: европейский журнал. 13 (29): 8240–8247. Дои:10.1002 / chem.200700365. PMID 17639522.
- ^ Морелл, Кристоф; Гранд, Андре; Торо-Лаббе, Алехандро (1 января 2005 г.). «Новый двойной дескриптор химической реакционной способности». Журнал физической химии A. 109 (1): 205–212. Bibcode:2005JPCA..109..205M. Дои:10.1021 / jp046577a. HDL:10533/176692. PMID 16839107.
- ^ Фарахани, Пурия; Баадер, Вильгельм Дж. (2017-02-16). «Механизм мономолекулярного разложения 1,2-диоксетандиона: согласованный или двунаправленный? Вот в чем вопрос!». Журнал физической химии A. 121 (6): 1189–1194. Bibcode:2017JPCA..121.1189F. Дои:10.1021 / acs.jpca.6b10365. ISSN 1089-5639. PMID 28094939.
- ^ Hickenboth, Charles R .; Мур, Джеффри С .; White, Scott R .; Соттос, Нэнси Р.; Бодри, Жером; Уилсон, Скотт Р. (2007). «Смещение реакционных путей с помощью механической силы». Природа. 446 (7134): 423–7. Bibcode:2007Натура.446..423H. Дои:10.1038 / природа05681. PMID 17377579.
- ^ Кори, Э. Дж. (2004). «Невозможные мечты». Журнал органической химии. 69 (9): 2917–9. Дои:10.1021 / jo049925d. PMID 15104426.
- ^ Джонсон, Кэролайн Ю. (1 марта 2005 г.) Чья это была идея?. Бостон Глобус
- ^ Хоффманн, Роальд (2004). "Заявление о развитии пограничного орбитального объяснения электроциклических реакций". Angewandte Chemie International Edition. 43 (48): 6586–90. Дои:10.1002 / anie.200461440. PMID 15558636.
- ^ Кори, Э. Дж .; Хортманн, Альфред Г. (1963). «Полный синтез дигидрокостунолида». Журнал Американского химического общества. 85 (24): 4033. Дои:10.1021 / ja00907a030.
- ^ Кори, Э. Дж .; Хортманн, Альфред Г. (1965). «Полный синтез дигидрокостунолида». Журнал Американского химического общества. 87 (24): 5736–42. Дои:10.1021 / ja00952a037. PMID 5845424.



























