Точка Ферма - Fermat point

Рис. 1. Построение первого изогонического центра X (13). Когда ни один угол треугольника не превышает 120 °, эта точка является точкой Ферма.

В геометрия, то Точка Ферма из треугольник, также называемый Точка Торричелли или же Точка Ферма – Торричелли, - это такая точка, что общее расстояние от трех вершин треугольника до точки является минимально возможным.[1] Он назван так потому, что впервые эта проблема была поднята Ферма в частном письме к Евангелиста Торричелли, кто это решил.

Точка Ферма дает решение геометрическая медиана и Проблемы дерева Штейнера на три балла.

Строительство

Точка Ферма треугольника с наибольшим углом не более 120 ° - это просто его точка. первый изогонический центр или же Х (13), который строится следующим образом:

  1. Построить равносторонний треугольник на каждой из двух произвольно выбранных сторон данного треугольника.
  2. Проведите линию от каждого нового вершина в противоположную вершину исходного треугольника.
  3. Две прямые пересекаются в точке Ферма.

Альтернативный метод следующий:

  1. На каждой из двух произвольно выбранных сторон постройте равнобедренный треугольник, с основанием рассматриваемой стороны, 30-градусными углами у основания и третьей вершиной каждого равнобедренного треугольника, лежащей вне исходного треугольника.
  2. Для каждого равнобедренного треугольника нарисуйте круг, в каждом случае с центром в новой вершине равнобедренного треугольника и с радиусом, равным каждой из двух новых сторон этого равнобедренного треугольника.
  3. Пересечение внутри исходного треугольника между двумя окружностями и есть точка Ферма.

Когда треугольник имеет угол больше 120 °, точка Ферма расположена в вершине с тупым углом.

В дальнейшем «Случай 1» означает, что угол треугольника превышает 120 °. «Случай 2» означает, что угол треугольника не превышает 120 °.

Расположение X (13)

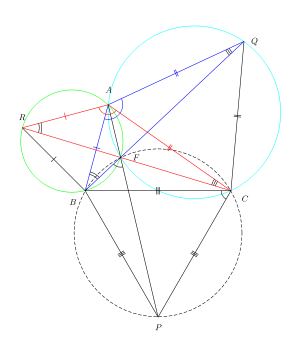
Рис 2. Геометрия первого изогонического центра.

На рис.2 показаны равносторонние треугольники ARB, AQC и CPB, прикрепленные к сторонам произвольного треугольника ABC. Вот доказательство, использующее свойства конциклические точки чтобы показать, что три прямые RC, BQ и AP на рис. 2 все пересекаются в точке F и пересекают друг друга под углом 60 °.

Треугольники RAC и BAQ - это конгруэнтный поскольку второе - это поворот первого на 60 ° относительно A. Следовательно, ARF = ∠ABF и ∠AQF = ∠ACF. Обратно к теорема о вписанном угле применительно к отрезку AF точки ARBF конциклический (они лежат по кругу). Точно так же точки AFCQ совпадают.

∠ARB = 60 °, поэтому ∠AFB = 120 °, используя теорема о вписанном угле. Аналогично ∠AFC = 120 °.

Итак, ∠BFC = 120 °. Таким образом, ∠BFC и ∠BPC в сумме составляют 180 °. С использованием теорема о вписанном угле, это означает, что точки BPCF совпадают. Итак, используя теорема о вписанном угле применительно к сегменту BP, BFP = ∠BCP = 60 °. Поскольку ∠BFP + ∠BFA = 180 °, точка F лежит на отрезке AP. Итак, линии RC, BQ и AP являются одновременный (они пересекаются в одной точке). Q.E.D.

Это доказательство применимо только в случае 2, поскольку, если ∠BAC> 120 °, точка A лежит внутри описанной окружности BPC, которая меняет взаимное расположение точек A и F. Однако его легко изменить, чтобы охватить случай 1. Тогда ∠AFB = ∠AFC = 60 °, следовательно, ∠BFC = ∠AFB = ∠AFC = 120 °, что означает, что BPCF является конциклическим, поэтому ∠BFP = ∠BCP = 60 ° = ∠BFA. Следовательно, A лежит на FP.

Линии, соединяющие центры окружностей на рис. 2, перпендикулярны отрезкам AP, BQ и CR. Например, линия, соединяющая центр круга, содержащего ARB, и центр круга, содержащего AQC, перпендикулярна сегменту AP. Итак, линии, соединяющие центры окружностей, также пересекаются под углом 60 °. Следовательно, центры окружностей образуют равносторонний треугольник. Это известно как Теорема Наполеона.

Расположение точки Ферма

Традиционная геометрия

Рис 3. Геометрия точки Ферма.

Для любого евклидова треугольника ABC и произвольной точки P пусть d (P) = PA + PB + PC, где PA обозначает расстояние между P и A. Цель этого раздела - идентифицировать точку P0 такое, что d (P0) 0. Если такая точка существует, то это будет точка Ферма. Далее ∆ будет обозначать точки внутри треугольника и включать его границу Ω.

Ключевой результат, который будет использоваться, - это правило изгиба, которое утверждает, что если треугольник и многоугольник имеют одну общую сторону, а остальная часть треугольника лежит внутри многоугольника, тогда треугольник имеет более короткий периметр, чем многоугольник.
[Если AB - общая сторона, расширьте AC, чтобы разрезать многоугольник в точке X. Тогда по неравенству треугольника периметр многоугольника> AB + AX ​​+ XB = AB + AC + CX + XB ≥ AB + AC + BC.]

Пусть P - любая точка вне Δ. Свяжите каждую вершину с ее удаленной зоной; то есть полуплоскость за (расширенной) противоположной стороной. Эти 3 зоны покрывают всю плоскость, за исключением самого Δ, и P явно лежит в одной или двух из них. Если P находится в двух точках (скажем, пересечение зон B и C), то установка P '= A влечет d (P') = d (A) для любой точки P вне Δ существует точка P 'в Ω такая, что d (P') .

Случай 1. Треугольник имеет угол ≥ 120 °.

Без ограничения общности предположим, что угол при A ≥ 120 °. Постройте равносторонний треугольник AFB и для любой точки P в Δ (кроме самой A) постройте Q так, чтобы треугольник AQP был равносторонним и имел указанную ориентацию. Тогда треугольник ABP представляет собой поворот на 60 ° треугольника AFQ вокруг A, так что эти два треугольника конгруэнтны, и отсюда следует, что d (P) = CP + PQ + QF, что является просто длиной пути CPQF. Поскольку P ограничено лежать в пределах ABC, по правилу изгиба длина этого пути превышает AC + AF = d (A). Следовательно, d (A) точка Ферма лежит в тупоугольной вершине.

Случай 2. Треугольник не имеет угла ≥ 120 °.

Постройте равносторонний треугольник BCD и пусть P - любая точка внутри Δ, и постройте равносторонний треугольник CPQ. Тогда CQD - это поворот CPB на 60 ° относительно C, поэтому d (P) = PA + PB + PC = AP + PQ + QD, что является просто длиной пути APQD. Пусть P0 - точка пересечения AD и CF. Эту точку принято называть первым изогоническим центром. Выполните то же упражнение с P0 как вы это делали с P, и найдите точку Q0. Угловым ограничением P0 лежит внутри Δ, причем BCF - это поворот BDA на 60 ° относительно B, поэтому Q0 должно лежать где-то на AD. Поскольку CDB = 60 °, Q0 лежит между P0 и D, что означает AP0Q0D - прямая линия, поэтому d (P0) = AD. Более того, если P ≠ P0 то либо P, либо Q не будут лежать на AD, что означает d (P0) = AD 0) ≤ d (P ') следует, что d (P0) 0 - точка Ферма кривой Δ. Другими словами, точка Ферма совпадает с первым изогоническим центром.

Векторный анализ

Позволять О, А, B, C, Икс быть любыми пятью точками на плоскости. Обозначим векторы к а, б, c, Икс соответственно, и пусть я, j, k быть единичными векторами из О вдоль а, б, c.
Сейчас |а| = а⋅и = (а − Икс)⋅i + x⋅i ≤ |а − Икс| + x⋅i и аналогично |б| ≤ |б − Икс| + x⋅j и |c| ≤ |c − Икс| + x⋅k.
Добавление дает |а| + |б| + |c| ≤ |а − Икс| + |б − Икс| + |c − Икс| + x⋅(я + j + k).
Если а, б, c встретиться в О под углами 120 °, то я + j + k = 0 так |а| + |б| + |c| ≤ |а − Икс| + |б − Икс| + |c − Икс| для всех Икс.
Другими словами, OA + OB + OC ≤ XA + XB + XC и поэтому О точка Ферма ABC.
Этот аргумент неверен, когда треугольник имеет угол ∠C > 120 °, потому что нет смысла О куда а, б, c встречаются под углами 120 °. Тем не менее, это легко исправить, переопределив k = − (я + j) и размещение О в C так что c = 0. Обратите внимание, что |k| ≤ 1, поскольку угол между единичными векторами я и j является ∠C что превышает 120 °. Поскольку |0| ≤ |0 − Икс| + x⋅k третье неравенство остается в силе, два других не изменяются. Доказательство продолжается, как указано выше (добавляя три неравенства и используя я + j + k = 0), чтобы прийти к тому же выводу, что О (или в этом случае C) должна быть точкой Ферма ABC.

Множители Лагранжа

Другой подход к поиску точки внутри треугольника, откуда сумма расстояний до вершины треугольника минимальна, нужно использовать один из оптимизация (математика) методы. В частности, метод Множители Лагранжа и закон косинусов.

Мы проводим линии от точки внутри треугольника к его вершинам и называем их Икс, Y и Z. Кроме того, пусть длины этих линий равны x, y и z соответственно. Пусть угол между Икс и Y быть α, Y и Z быть β. Тогда угол между Икс и Z есть (2π - α - β). Используя метод множителей Лагранжа, нужно найти минимум лагранжиана L, что выражается как:

L = Икс + у + z + λ1 (Икс2 + у2 − 2ху cos (α) − а2) + λ2 (у2 + z2 − 2yz cos (β) - б2) + λ3 (z2 + Икс2 − 2zx cos (α + β) − c2)

куда а, б и c - длины сторон треугольника.

Приравнивая каждую из пяти частных производных δL/ δx, δL/ δy, δL/ δz, δL/ δα, δL/ δβ к нулю и исключив λ1, λ2, λ3 в конечном итоге дает sin (α) = sin (β) и sin (α + β) = - sin (β), поэтому α = β = 120 °. Однако устранение - долгое и утомительное дело, и конечный результат охватывает только случай 2.

Характеристики

Два изогонических центра являются пересечением трех vesicae piscis чьи парные вершины являются вершинами треугольника
  • Когда наибольший угол треугольника не превышает 120 °, Икс(13) - точка Ферма.
  • Углы, образуемые сторонами треугольника при Икс(13) все равны 120 ° (Случай 2) или 60 °, 60 °, 120 ° (Случай 1).
  • В окружности из трех построенных равносторонних треугольников совпадают в Икс(13).
  • Трилинейные координаты для первого изогонического центра, Икс(13):
csc (А + π / 3): csc (B + π / 3): csc (C + π / 3), или, что то же самое,
сек (А - π / 6): сек (B - π / 6): сек (C - π / 6).[2]
csc (А - π / 3): csc (B - π / 3): csc (C - π / 3), или, что то же самое,
сек (А + π / 6): сек (B + π / 6): сек (C + π / 6).[3]
1 − ты + uvw сек (А - π / 6): 1 - v + uvw сек (B - π / 6): 1 - ш + uvw сек (C - π / 6)
куда u, v, w соответственно обозначим Булевы переменные (А<120°), (B<120°), (C<120°).
грех (А + π / 3): грех (B + π / 3): грех (C + π / 3).[4]
грех (А - π / 3): грех (B - π / 3): грех (C - π / 3).[5]
  • Следующие треугольники равносторонние:
антипедальный треугольник из Икс(13)
антипедальный треугольник Икс(14)
педальный треугольник из Икс(15)
педальный треугольник Икс(16)
окружной треугольник Икс(15)
окружной треугольник Икс(16)

Псевдонимы

В изогонические центры Икс(13) и Икс(14) также известны как первая точка Ферма и вторая точка Ферма соответственно. Альтернативами являются положительная точка Ферма и отрицательная точка Ферма. Однако эти разные имена могут сбивать с толку, и, возможно, их лучше избегать. Проблема в том, что в большей части литературы стирается различие между Точка Ферма и первая точка Ферма тогда как только в приведенном выше случае 2 они фактически одинаковы.

История

Этот вопрос был предложен Ферма как вызов Евангелиста Торричелли. Он решил проблему так же, как и Ферма, но вместо этого использовал пересечение описанных окружностей трех правильных треугольников. Его ученица Вивиани опубликовала решение в 1659 году.[8]

Смотрите также

Рекомендации

  1. ^ Разрежьте узел - точка Ферма и обобщения
  2. ^ Запись X (13) в Энциклопедия центров треугольников В архиве 19 апреля 2012 г. Wayback Machine
  3. ^ Запись X (14) в Энциклопедия центров треугольников В архиве 19 апреля 2012 г. Wayback Machine
  4. ^ Запись X (15) в Энциклопедия центров треугольников В архиве 19 апреля 2012 г. Wayback Machine
  5. ^ Запись X (16) в Энциклопедия центров треугольников В архиве 19 апреля 2012 г. Wayback Machine
  6. ^ Кимберлинг, Кларк. «Энциклопедия треугольных центров».
  7. ^ Кристофер Дж. Брэдли и Джефф С. Смит, «Расположение центров треугольников», Форум Geometricorum 6 (2006), 57--70. http://forumgeom.fau.edu/FG2006volume6/FG200607index.html
  8. ^ Вайсштейн, Эрик В. «Ферма Очки». MathWorld.

внешняя ссылка