Гиперфокальное расстояние - Hyperfocal distance

Камера Minox LX с гиперфокальной красной точкой

В оптика и фотография, гиперфокальное расстояние это расстояние, за которое все объекты могут быть приведены в «приемлемый» фокус. Поскольку гиперфокальное расстояние - это фокусное расстояние, обеспечивающее максимальное глубина резкости, это наиболее желаемое расстояние для установки фокуса камера с фиксированным фокусом.^[1] Гиперфокальное расстояние полностью зависит от того, какой уровень резкости считается приемлемым.

Гиперфокальное расстояние имеет свойство, называемое «последовательной глубиной резкости», когда линза фокусируется на объекте, расстояние которого находится на гиперфокальном расстоянии. ЧАС будет удерживать глубину резкости от ЧАС/ 2 до бесконечности, если объектив сфокусирован на ЧАС/ 2, глубина резкости будет от ЧАС/ 3 к ЧАС; если линза затем сфокусирована на ЧАС/ 3, глубина резкости будет от ЧАС/ 4 к ЧАС/ 2 и др.

Томас Саттон и Джордж Доусон впервые написал о гиперфокальном расстоянии (или «фокусном диапазоне») в 1867 году.^[2] Луи Дерр в 1906 году, возможно, был первым, кто вывел формулу для гиперфокального расстояния. Рудольф Кингслейк писал в 1951 году о двух методах измерения гиперфокального расстояния.

У некоторых камер гиперфокальное расстояние указано на шкале фокусировки. Например, на шкале фокусировки Minox LX есть красная точка между 2 м и бесконечностью; когда объектив установлен на красную точку, то есть сфокусирован на гиперфокальном расстоянии, глубина резкости увеличивается от 2 м до бесконечности.

Два метода

Есть два распространенных метода определения и измерения гиперфокальное расстояние, что приводит к незначительно различающимся значениям. Различие между этими двумя значениями проводится редко, поскольку они имеют почти идентичные значения. Значение, вычисленное в соответствии с первым определением, превышает значение, полученное во втором, всего на один фокусное расстояние.

Определение 1: Гиперфокальное расстояние - это ближайшее расстояние, на котором линза можно сосредоточиться, сохраняя объекты на бесконечности приемлемо резкое. Когда объектив сфокусирован на этом расстоянии, все объекты на расстоянии от половины гиперфокального расстояния до бесконечности будут приемлемо резкими.

Определение 2: Гиперфокальное расстояние - это расстояние, за пределами которого все объекты становятся приемлемо резкими для линзы, сфокусированной на бесконечность.

Приемлемая резкость

Гиперфокальное расстояние полностью зависит от того, какой уровень резкости считается приемлемым. Критерий желаемой приемлемой резкости указывается через круг замешательства (CoC) предел диаметра. Этот критерий представляет собой наибольший допустимый диаметр пятна, до которого может распространяться бесконечно малая точка на носителе изображения (пленке, цифровом датчике и т. Д.).

Формулы

Для первого определения

${ displaystyle H = { frac {f ^ {2}} {Nc}} + f}$

куда

${ displaystyle H}$ гиперфокальное расстояние

${ displaystyle f}$ является фокусное расстояние

${ displaystyle N}$ является f-число (${ displaystyle f / D}$ для диаметра отверстия ${ displaystyle D}$)

${ displaystyle c}$ это круг замешательства предел

Для любого практического f-числа добавленное фокусное расстояние незначительно по сравнению с первым членом, так что

${ Displaystyle H приблизительно { гидроразрыва {f ^ {2}} {Nc}}}$

Эта формула точна для второго определения, если ${ displaystyle H}$ измеряется от тонкой линзы или от передней главной плоскости сложной линзы; он также точен для первого определения, если ${ displaystyle H}$ измеряется от точки, которая находится на расстоянии одного фокусного расстояния от передней главной плоскости. Для практических целей разница между первым и вторым определениями небольшая.

Вывод с помощью геометрической оптики

Сопровождающие цифры

Следующие ниже выводы относятся к прилагаемым рисункам. Для наглядности указаны половина апертуры и кружок нерезкости.^[3]

Определение 1

Объект на расстоянии ЧАС формирует резкое изображение на расстоянии Икс (Синяя линия). Здесь объекты на бесконечности имеют изображения с кружком нерезкости, обозначенным коричневым эллипсом, где верхний красный луч, проходящий через точку фокусировки, пересекает синюю линию.

Сначала используя подобные треугольники, заштрихованные зеленым,

${ displaystyle { begin {array} {crcl} & { dfrac {xf} {c / 2}} & = & { dfrac {f} {D / 2}} поэтому & x-f & = & { dfrac {cf} {D}} поэтому & x & = & f + { dfrac {cf} {D}} end {array}}}$

Затем, используя аналогичные треугольники с фиолетовыми точками,

${ displaystyle { begin {array} {crclcl} & { dfrac {H} {D / 2}} & = & { dfrac {x} {c / 2}} поэтому & H & = & { dfrac {Dx} {c}} & = & { dfrac {D} {c}} { Big (} f + { dfrac {cf} {D}} { Big)} && = & { dfrac { Df} {c}} + f & = & { dfrac {f ^ {2}} {Nc}} + f end {array}}}$

как указано выше.

Определение 2

Объекты, находящиеся на бесконечности, формируют четкие изображения на фокусном расстоянии ж (Синяя линия). Здесь объект на ЧАС формирует изображение с кружком нерезкости, обозначенным коричневым эллипсом, где нижний красный луч, сходящийся к его резкому изображению, пересекает синюю линию.

Используя подобные треугольники, заштрихованные желтым цветом,

${ displaystyle { begin {array} {crclcl} & { dfrac {H} {D / 2}} & = & { dfrac {f} {c / 2}} поэтому & H & = & { dfrac {Df} {c}} & = & { dfrac {f ^ {2}} {Nc}} end {array}}}$

Пример

---

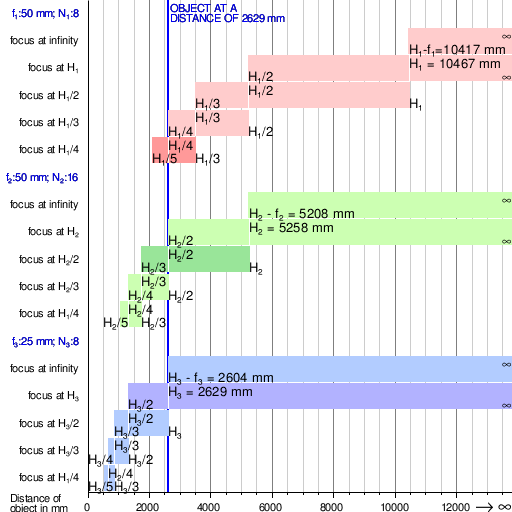
Глубина резкости из 3 идеальных линзы из фокусные расстояния, ж₁, ж₂ и ж₃, и f-числа N₁, N₂ и N₃ при фокусировке на объекты на разном расстоянии. ЧАС₁, ЧАС₂ и ЧАС₃ обозначим их соответствующие гиперфокальные расстояния (с помощью Определение 1 в эта статья ) с круг замешательства диаметром 0,03 мм. Более темные полосы показывают, как для фиксированного расстояния до объекта глубина резкости увеличивается за счет использования более короткого фокусного расстояния или меньшей диафрагмы. Вторая самая верхняя полоса каждого набора иллюстрирует конфигурацию для фиксированный фокус камера с фокусом, постоянно установленным на гиперфокальном расстоянии, чтобы максимизировать глубину резкости.

Например, для объектива 50 мм при ${ displaystyle f / 8}$ используя кружок нерезкости 0,03 мм, значение, обычно используемое в фотографии 35 мм, гиперфокальное расстояние в соответствии с Определение 1 является

${ displaystyle H = { frac {(50) ^ {2}} {(8) (0,03)}} + (50) = 10467 { mbox {мм}}}$

Если объектив сфокусирован на расстоянии 10,5 м, то все от половины этого расстояния (5,2 м) до бесконечности будет приемлемо резким на нашей фотографии. С формулой для Определение 2, результат 10417 мм, разница 0,5%.

Последовательные глубины резкости

У гиперфокального расстояния есть любопытное свойство: в то время как линза сфокусирована на ЧАС будет удерживать глубину резкости от ЧАС/ 2 до бесконечности, если объектив сфокусирован на ЧАС/ 2, глубина резкости будет от ЧАС/ 3 к ЧАС; если линза затем сфокусирована на ЧАС/ 3, глубина резкости будет от ЧАС/ 4 к ЧАС/ 2. Это продолжается на протяжении всех последующих 1 /Икс значения гиперфокального расстояния.

Пайпер (1901) называет это явление «последовательной глубиной резкости» и показывает, как легко проверить эту идею. Это также одна из первых публикаций, в которых слово гиперфокальный.

Рисунок справа иллюстрирует это явление.

История

Это раннее использование термина гиперфокальное расстояние, Derr 1906, никоим образом не является самым ранним объяснением этой концепции.

Концепции двух определений гиперфокального расстояния имеют долгую историю, связанную с терминологией глубины резкости, глубины резкости, круга нерезкости и т. Д. Вот некоторые избранные ранние цитаты и интерпретации по этой теме.

Саттон и Доусон 1867

Томас Саттон и Джордж Доусон определяют фокусное расстояние для того, что мы сейчас называем гиперфокальное расстояние:^[2]

Фокусное расстояние. В каждой линзе есть, соответствующая заданному апертальному отношению (то есть отношению диаметра диафрагмы к фокусному расстоянию), определенное расстояние от ближайшего объекта от него, между которым и бесконечностью все объекты находятся в одинаковом хорошем состоянии. фокус. Например, в объективе с одним обзором с фокусным расстоянием 6 дюймов с шагом 1/4 дюйма (апертальное отношение одна двадцать четвертая) все объекты расположены на расстоянии 20 футов от объектива и на бесконечном расстоянии от него ( неподвижная звезда, например) одинаково хорошо сфокусированы. Поэтому двадцать футов называют «фокусным диапазоном» объектива, когда используется этот стоп. Следовательно, диапазон фокусировки - это расстояние до ближайшего объекта, который будет хорошо сфокусирован, если матовое стекло настроено на очень удаленный объект. В одном и том же объективе диапазон фокусных расстояний будет зависеть от размера используемой диафрагмы, в то время как в разных объективах с одинаковым апертальным отношением диапазоны фокусных расстояний будут больше при увеличении фокусного расстояния объектива. «фокусный диапазон» не вошел в широкое употребление, но очень желательно, чтобы они вошли в употребление, чтобы предотвратить двусмысленность и неопределенность при рассмотрении свойств фотографических линз. «Диапазон фокусировки» - это хороший термин, потому что он выражает диапазон, в пределах которого необходимо настроить фокусировку объектива на объекты на разном расстоянии от него - другими словами, диапазон, в котором становится необходима фокусировка.

Их фокусный диапазон примерно в 1000 раз больше диаметра апертуры, поэтому он имеет смысл в качестве гиперфокального расстояния со значением CoC равным. ж/ 1000, или диагональ формата изображения, умноженная на 1/1000, при условии, что это «нормальный» объектив. Однако неясно, был ли указанный фокусный диапазон вычисленным или эмпирическим.

Эбни 1881

Сэр Уильям де Вивелсли Эбни говорит:^[4]

Прилагаемая формула приблизительно даст ближайшую точку п который появится в фокусе, когда расстояние будет точно сфокусировано, предполагая, что допустимый диск нерезкости равен 0,025 см:

${ displaystyle p = 0,41 cdot f ^ {2} cdot a}$

когда

${ displaystyle f =}$ фокусное расстояние объектива в см

${ displaystyle a =}$ отношение диафрагмы к фокусному расстоянию

То есть, а является обратным тому, что мы сейчас называем ж-число, а ответ явно в метрах. Его 0,41, очевидно, должно быть 0,40. На основе его формул и представления о том, что светосила Эбни говорит:

Можно показать, что увеличение с небольшого негатива лучше, чем изображение того же размера, сделанное напрямую, в отношении резкости деталей. ... Следует проявлять осторожность, чтобы различать преимущества, которые можно получить при увеличении за счет использования линз меньшего размера, и недостатки, возникающие в результате ухудшения относительных значений света и тени.

Тейлор 1892

Джон Трэйл Тейлор вспоминает эту словесную формулу для обозначения гиперфокального расстояния:^[5]

Мы видели, как некоторые авторы по оптике (Томас Саттон, если мы правильно помним) сформулировали как приблизительное правило, что если диаметр стопа составляет сороковую часть фокуса линзы, глубина резкости будет колебаться между бесконечность и расстояние в четыре раза больше футов, чем дюймов в фокусе линзы.

Эта формула подразумевает более строгий критерий CoC, чем мы обычно используем сегодня.

Ходжес 1895

Джон Ходжес обсуждает глубину резкости без формул, но с некоторыми из этих соотношений:^[6]

Однако есть момент, за пределами которого все будет в хорошем изображении, но чем дольше используется фокус объектива, тем дальше удаляется точка, за которой все находится в резком фокусе. С математической точки зрения, глубина линзы обратно пропорциональна квадрату ее фокуса.

Эта «математически» наблюдаемая взаимосвязь подразумевает, что у него была под рукой формула и параметризация с f-числом или «отношением интенсивности» в ней. Чтобы получить отношение обратных квадратов к фокусному расстоянию, вы должны предположить, что предел CoC фиксирован, а диаметр апертуры масштабируется с фокусным расстоянием, давая постоянное f-число.

Пайпер 1901

К. Велборн Пайпер может быть первым, кто опубликовал четкое различие между Глубина резкости в современном понимании и Глубина определения в фокальной плоскости и означает, что Глубина резкости и Глубина расстояния иногда используются для первых (в современном использовании, Глубина резкости обычно зарезервировано для последних).^[7] Он использует термин Постоянная глубины за ЧАС, и измеряет его от переднего главного фокуса (т.е. он считает на одно фокусное расстояние меньше расстояния от объектива, чтобы получить более простую формулу), и даже вводит современный термин:

Это максимально возможная глубина резкости, и ЧАС + ж может быть стилизован под расстояние максимальной глубины резкости. Если измерить это расстояние экстрафокально, оно равно ЧАС, и иногда его называют гиперфокальным расстоянием. Постоянная глубины и гиперфокальное расстояние довольно разные, хотя и имеют одинаковое значение.

Непонятно, какое различие он имеет в виду. Рядом с таблицей I в своем приложении он отмечает:

Если мы сфокусируемся на бесконечности, константа - это фокусное расстояние до ближайшего объекта в фокусе. Если мы сфокусируемся на внефокусном расстоянии, равном константе, мы получим максимальную глубину резкости примерно от половины постоянного расстояния до бесконечности. Тогда константа - это гиперфокальное расстояние.

На данный момент у нас нет доказательств использования термина гиперфокальный перед Пайпер, ни дефис гиперфокальный который он также использовал, но он, очевидно, не претендовал на создание этого дескриптора сам.

Derr 1906

Луи Дерр может быть первым, кто четко определил первое определение:^[8] который в наше время считается строго правильным, и вывести соответствующую ему формулу. С помощью ${ displaystyle p}$ для гиперфокального расстояния, ${ displaystyle D}$ для диаметра отверстия, ${ displaystyle d}$ для диаметра, которого не должен превышать круг нерезкости, и ${ displaystyle f}$ для фокусного расстояния он выводит:

${ displaystyle p = { frac {(D + d) f} {d}}}$ [1]

Как диаметр апертуры, ${ displaystyle D}$ это отношение фокусного расстояния, ${ displaystyle f}$ к числовой апертуре, ${ displaystyle N}$; и диаметр круга нерезкости, ${ displaystyle c = d}$, это дает уравнение для первого определения выше.

${ displaystyle p = { frac {({ tfrac {f} {N}} + c) f} {c}} = { frac {f ^ {2}} {Nc}} + f}$

Джонсон 1909

Джордж Линдси Джонсон использует термин Глубина резкости по тому, что назвал Эбни Глубина резкости, и Глубина резкости в современном понимании (возможно, впервые),^[9] как допустимая ошибка расстояния в фокальной плоскости. Его определения включают гиперфокальное расстояние:

Глубина резкости - удобный, но не совсем точный термин, используемый для описания количества рывков (вперед или назад), которые могут быть переданы экрану без заметного размытия изображения, то есть без размытия изображения, превышающего 1 / 100 дюймов, или в случае увеличиваемых негативов или научных работ - 1/10 или 1/100 мм. Затем ширина световой точки, которая, конечно, вызывает размытие с обеих сторон, т.е. 1/50 дюйма = 2е (или 1/100 дюйма = е).

Его рисунок дает понять, что его е - радиус круга нерезкости. Он ясно предвидел необходимость привязки его к размеру формата или увеличению, но не дал общей схемы для его выбора.

Глубина резкости в точности совпадает с глубиной резкости, только в первом случае глубина измеряется движением пластины при фиксированном объекте, а во втором случае глубина измеряется расстоянием, на которое объект может перемещаться без круга замешательства, превышающего 2е.

Таким образом, если объектив, сфокусированный на бесконечность, по-прежнему дает резкое изображение объекта на расстоянии 6 ярдов, его глубина резкости составляет от бесконечности до 6 ярдов, причем каждый объект за пределами 6 ярдов оказывается в фокусе.

Это расстояние (6 ярдов) называется гиперфокальное расстояние линзы, и любой допустимый диск путаницы зависит от фокусного расстояния объектива и используемого упора.

Если предел запутанности половины диска (т.е. е) принимается равным 1/100 дюйма, тогда гиперфокальное расстояние

${ displaystyle H = { frac {Fd} {e}}}$,

d диаметр упора, ...

Использование Джонсоном бывший и последний вроде бы поменялись местами; возможно бывший здесь имелся в виду ссылка на непосредственно предшествующий заголовок раздела Глубина резкости, и последний к текущему заголовку раздела Глубина резкости. За исключением очевидной ошибки коэффициента 2 при использовании отношения диаметра упора к радиусу CoC, это определение совпадает с гиперфокальным расстоянием Абни.

Другие, начало ХХ века

Период, термин гиперфокальное расстояние также появляется в книге Касселла Циклопедия 1911 г., Справочник Синклера по фотографии 1913 г. и Бейли Полный фотограф 1914 г.

Кингслейк 1951

Рудольф Кингслейк ясно говорит о двух значениях:^[1]

если камера сфокусирована на расстоянии s равный 1000 диаметров апертуры линзы, то большая глубина ${ displaystyle D_ {1}}$ становится бесконечным. Это критическое расстояние до объекта »час"известен как Гиперфокальное расстояние. Для камеры, сфокусированной на этом расстоянии, ${ Displaystyle D_ {1} = infty}$ и ${ displaystyle D_ {2} = h / 2}$, и мы видим, что диапазон приемлемых расстояний в фокусе будет составлять всего лишь половину гиперфокального расстояния до бесконечности. Следовательно, гиперфокальное расстояние является наиболее желательным расстоянием, на котором предварительно устанавливается фокус камеры с фиксированным фокусом. Также стоит отметить, что если камера сфокусирована на ${ displaystyle s = infty}$, ближайший приемлемый объект находится на ${ Displaystyle L_ {2} = ш / (ч + с) = ч / (ч / с + 1) = ч}$ (по уравнению 21). Это второе важное значение гиперфокального расстояния.

Кингслейк использует простейшие формулы для степеней свободы на ближних и дальних расстояниях, в результате чего два разных определения гиперфокального расстояния дают одинаковые значения.

Смотрите также

• Круг замешательства
• Глубокий фокус
• Депсси, индикатор глубины резкости восхода / захода солнца

Рекомендации

внешняя ссылка

• http://www.dofmaster.com/dofjs.html для расчета гиперфокального расстояния и глубина резкости